こんにちは!しゅんです!
今回の記事では同値類と同値類分割について解説していきます!
最近2項関係の勉強をしていたときに、同値類、同値類分割って単語が出てきました。見てみると数式が並んでいて理解するのが少し大変でした笑
ということでこの記事では同値類、同値類分割がだいたいどんな感じのイメージなのかを説明したいと思います!
それではやっていきましょう!
普段は統計検定2級の記事を書いてたりします。
ぜひ他の記事も読んでみてください!
このブログの簡単な紹介はこちらに書いてあります。
興味があったら見てみてください。
このブログでは経営工学を勉強している現役理系大学生が、経営工学に関することを色々話していきます!
ぼくが経営工学を勉強している中で感じたことや、興味深かったことを皆さんと共有出来たら良いなと思っています。
そもそも経営工学とは何なのでしょうか。Wikipediaによると
経営工学(けいえいこうがく、英: engineering management)は、人・材料・装置・情報・エネルギーを総合したシステムの設計・改善・確立に関する活動である。そのシステムから得られる結果を明示し、予測し、評価するために、工学的な分析・設計の原理・方法とともに、数学、物理および社会科学の専門知識と経験を利用する。
引用元 : 経営工学 – Wikipedia
長々と書いてありますが、要は経営、経済の課題を理系的な観点から解決する学問です。
まず最初に同値関係を知る
同値類・同値類分割というのは同値関係というものを使って定義されます。そのためまず最初に同値関係というものがどんなものなのかを知っておく必要があります。
ザックリ言うと同値関係とは
「同じものとみなせるペアを集めた集合」
です。
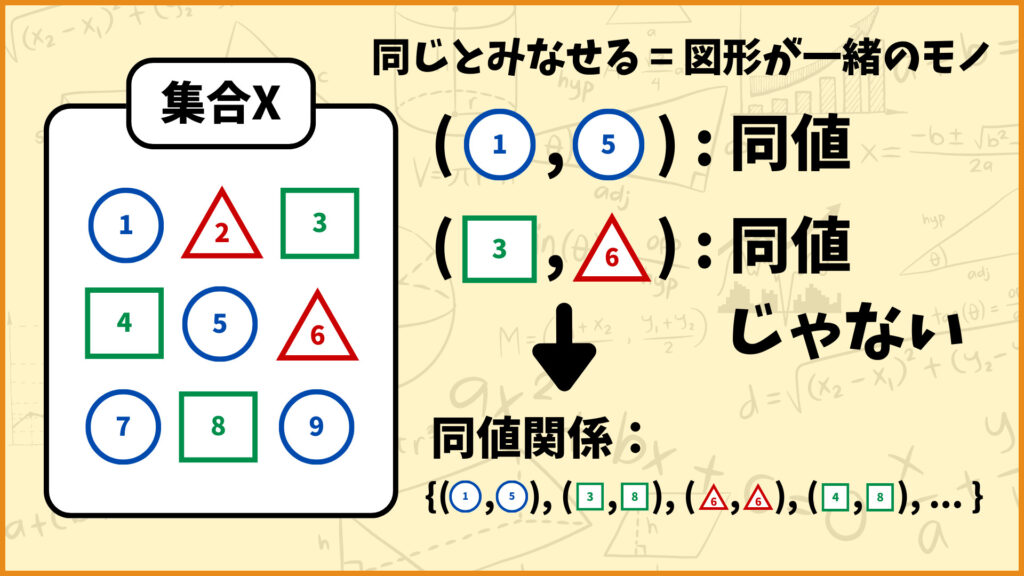
今集合\(X\)が存在し、集合\(X\)の中から2つの要素を選ぶことを考えます。このときに、選んだ2つの要素が同じとみなせるモノかそうではないかを判断します。今回は図形が一緒なモノを同じとみなすことにします。
そうすると例えば青〇の1と青〇の5は同値なペア、緑□の3と赤△の6は同値じゃないペアという風になります。このようにして同値なペアだけを全て集めたのが同値関係になります。
上の話はあくまで分かりやすさ優先な説明です。厳密な定義は「ある集合\(X\)上の2項関係の中で反射律・対称律・推移律を満たすもの」です。
より厳密な説明はこちらの記事で解説しています!
同値類ってなに?
ザックリとしたイメージ
それでは同値類の説明に入っていきたいと思います。同値類のザックリとしたイメージは
「ある要素と同値なモノだけを集めたもの」
です。
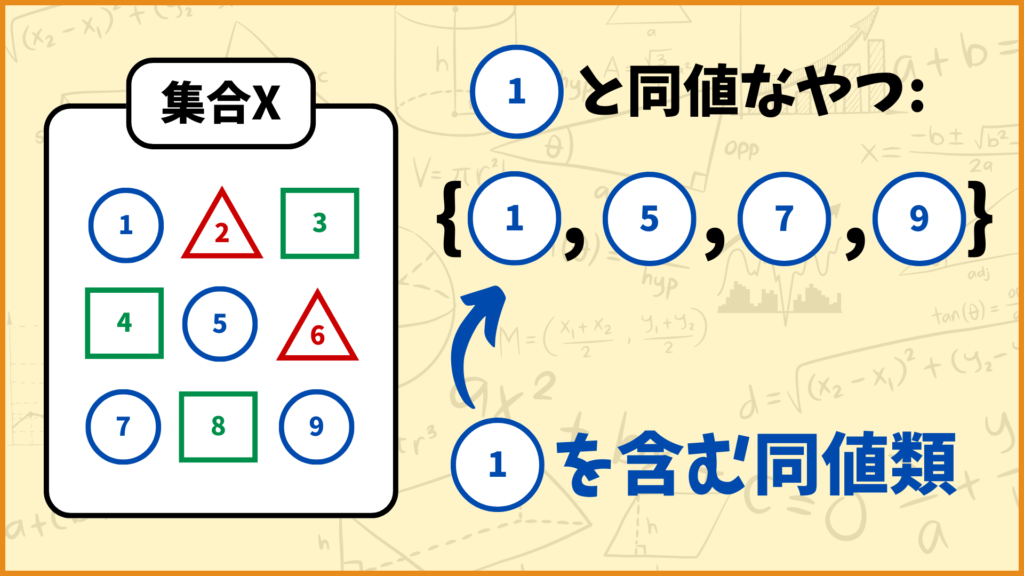
例えば上の例でいうと、青〇の1と同値なモノは青〇の1,5,7,9です。これらをまとめたものを(青〇の1を含む)同値類と言います。
ちゃんとした定義
同値類を数学的にちゃんと定義すると
ある集合\(X\)上の同値関係\(R\)が与えられたときに、集合\(X\)中の要素\(x \in X\)に対して(\(x\)を含む)同値類\([x]\)を
\( [x] = \{y \in X \; | \; (x,y) \in R\}\)
と定義する
となります。
この式の意味をちょっと考えてみましょう。同値類\([x]\)は\((x,y) \in R\)を満たす\(y\)を集めた集合ということです。\((x,y) \in R\)は\(x\)と\(y\)が同値関係にあるということを表しています。
つまり\(x\)と同値関係にある要素\(y\)を全て持ってきてくださいってことを言っています。
例えば
\(X=\{1,2,3,4,5\}\)
\(R=\{(1,1),(2,2),(3,3),(4,4),(5,5),(1,2),(2,3),(1,3),(2,1),(3,2),(3,1)\}\)
とします。このとき\([1]\)を求めてみましょう。
\((1,y) \in R\)を満たす\(y\)は1,2,3です。したがって\([1] = \{1,2,3\}\)となります。
同値類の性質として、任意の\(x,y \in X\)に対して\( [x] = [y]\)または\( [x] \cap [y] = \emptyset\)が成り立ちます。
より詳しく言うと\((x,y) \in R\)のときは\( [x] = [y]\)が成り立ち、\( (x,y) \notin R\)のときは\( [x] \cap [y] = \emptyset\)が成り立ちます。
上の例だと\([1] = [2] = [3] = \{1,2,3\},\; [4] = \{4\}, \; [5] = \{5\}\)となります。
同値類分割ってなに?
ザックリとしたイメージ
それでは次に同値類分割の説明に入っていきたいと思います。同値類分割のザックリとしたイメージは
「集合を同値類ごとに分割すること」
です。
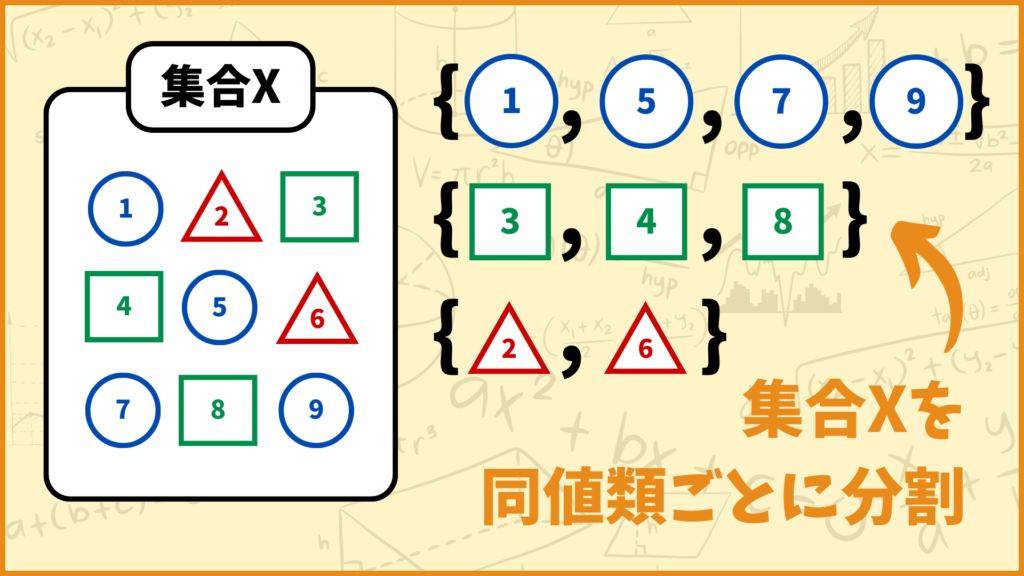
上の集合\(X\)を見てください。この集合に対して同じ図形のものを同値とします。このときの同値類は青〇、緑□、赤△の3種類です。
このように同値類によって集合を分割することを同値類分割と言います。
ちゃんとした定義
同値類分割を数学的にちゃんと定義すると
\( \{[x] \; | \; x \in X\}\)
となります。(同値類は商集合とも呼び\(X/R\)と書きます。)
\([x] = [y]\)となる要素\(x.y \in X\)があるから上の定義式だと分かりにくいかもしれません。
イメージ的には\([x] = [y]\)となるものはまとめちゃって、\([x] \cap [y] = \emptyset\)となるものだけを集めてきたみたいな感じです。
同値類のちゃんとした定義の所で使った
\(X=\{1,2,3,4,5\}\)
\(R=\{(1,1),(2,2),(3,3),(4,4),(5,5),(1,2),(2,3),(1,3),(2,1),(3,2),(3,1)\}\)
の例で言うと
\(X/R = \{\{1.2.3\},\{4\},\{5\}\}\)
となります。
グラフと同値類の関係
同値関係の例として、無向グラフのパスが挙げられます。より厳密に言うと無向グラフ\(G=(V,E)\)において頂点集合\(V\)上の2項関係\(R\)を
\(R = \{(v,w) \in V \times V \; | \; G\text{中に}v-w\text{路がある}\}\)
と定義するとき、この2項関係\(R\)は同値関係になります。
なぜこれが同値関係になるのかは下の記事で解説しています!
要は間にパスがある頂点は同値とみなせるよってことです。ではこのとき同値類は何を表すのでしょうか、下のグラフを使って確かめてみたいと思います。
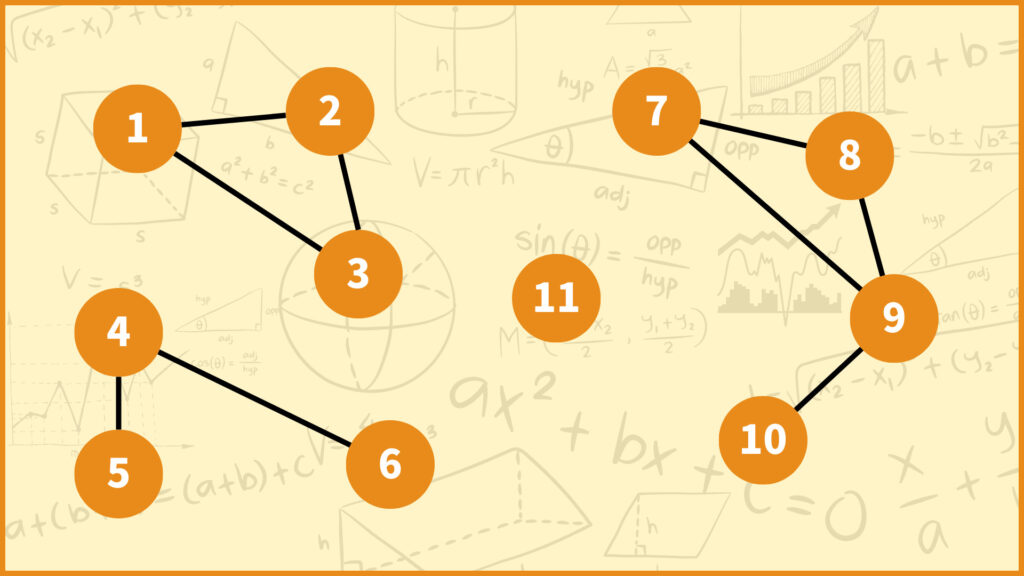
例えば頂点1と頂点2の間にはパスがあるので\((1,2) \in R\)となります。一方頂点6と頂点7の間にはパスがないので\((6,7) \notin R\)となります。
このように考えると例えば頂点1を含む同値類は\([1] = \{1,2,3\}\)となります。
他にも例えば頂点7を含む同値類は\([7] = \{7,8,9,10\}\)となります。
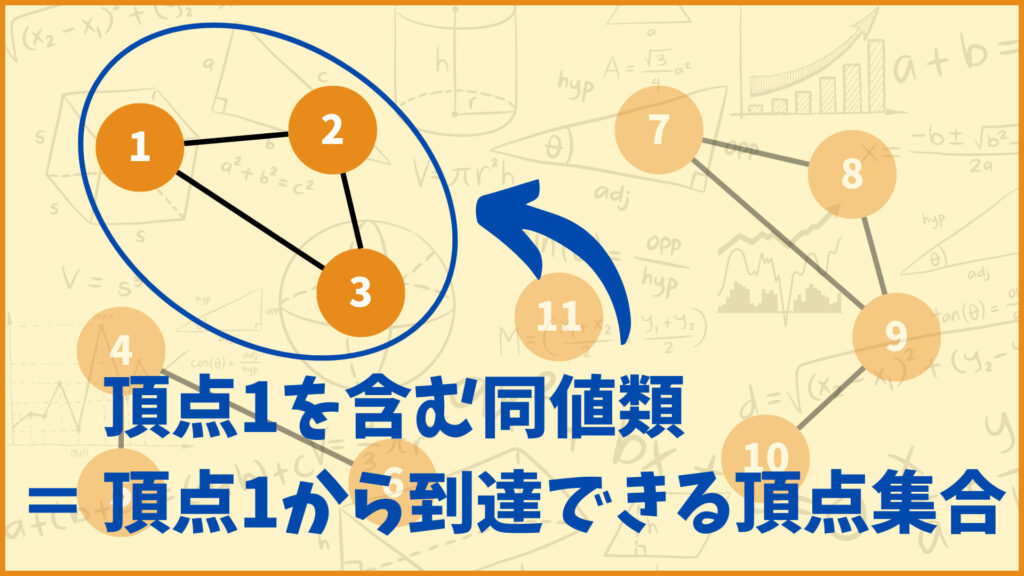
つまり無向グラフにおいて、上で定義した同値関係\(R\)による同値類は
「その頂点から到達することができる頂点の集合」
という風になります。
グラフと同値類分割の関係
今度は同値類分割について考えてみます。「グラフと同値類の関係」の所で使った同値関係\(R\)をここでも使いたいと思います。同値類は\([1],[2],…,[11]\)までありますが、いくつか重複しているやつがありますね。
例えば\([1]\)と\([2]\)と\([3]\)はどれも\(\{1,2,3\}\)で重複しています。これらを毎回書くのは冗長なので1つにまとめます。そのように考えると同値類分割は以下のようになります。
\(V / R = \{\{1,2,3\},\{4,5,6\},\{7,8,9,10\},\{11\}\}\)
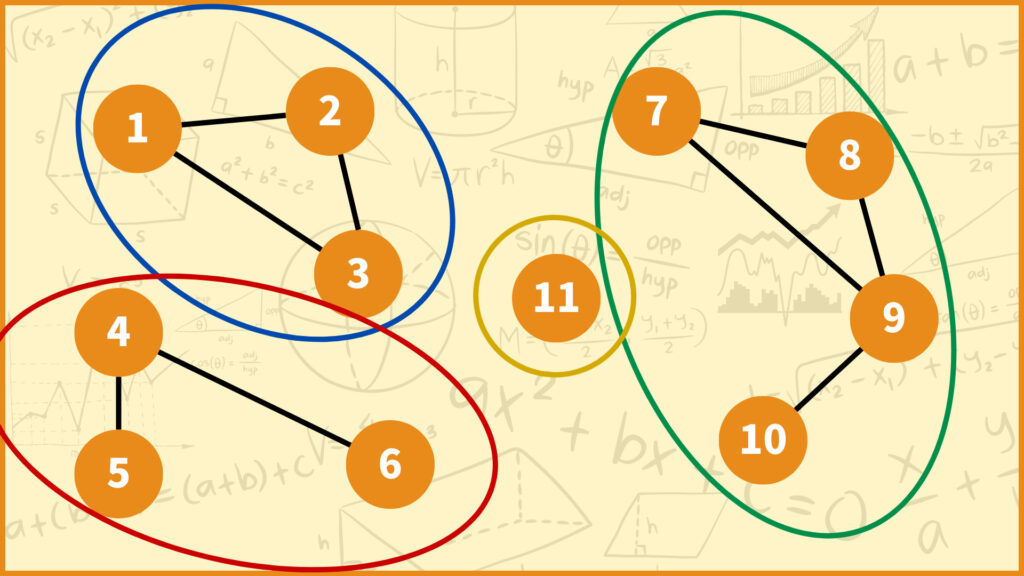
同値類分割を図で表すと上のようになります。各同値類を色で分けて囲みました。この図を見ると、同値類分割が連結成分に対応していることが分かります。
この記事では間にパスが存在する頂点を同値とみなしたときの話をしています。同値関係\(R\)を変えればまた異なる結果が得られます。
例えば下の2項関係
\(R = \{(e,f) \in E \times E \; | \; G\text{に辺}e\text{と辺}f\text{を通るサーキットがある}\}\)
は同値関係になりますが、この\(R\)による同値類分割はさきほどの話で得られた結果とは異なります。
おわりに
いかがでしたか。
今回の記事では同値類・同値類分割について解説していきました。
今後もこのような離散数学に関する記事を書いていきます!
最後までこの記事を読んでくれてありがとうございました。




