こんにちは!しゅんです!
今回の記事では機械が2台のフローショップ・スケジューリング問題を解く方法を解説したいと思います!
それではやっていきましょう!
今回解説したものをstreamlitでwebアプリにしました!
このサイトではジョブ数と各ジョブの各機械での処理時間を入力するだけで皆さんもフローショップ・スケジューリング問題を解くことができます!
普段は統計検定2級の記事を書いてたりします。
ぜひ他の記事も読んでみてください!
このブログの簡単な紹介はこちらに書いてあります。
興味があったら見てみてください。
このブログでは経営工学を勉強している現役理系大学生が、経営工学に関することを色々話していきます!
ぼくが経営工学を勉強している中で感じたことや、興味深かったことを皆さんと共有出来たら良いなと思っています。
そもそも経営工学とは何なのでしょうか。Wikipediaによると
経営工学(けいえいこうがく、英: engineering management)は、人・材料・装置・情報・エネルギーを総合したシステムの設計・改善・確立に関する活動である。そのシステムから得られる結果を明示し、予測し、評価するために、工学的な分析・設計の原理・方法とともに、数学、物理および社会科学の専門知識と経験を利用する。
引用元 : 経営工学 – Wikipedia
長々と書いてありますが、要は経営、経済の課題を理系的な観点から解決する学問です。
問題設定
問題設定:
・2台の機械、\(m\)個のジョブの場合のフローショップ・スケジューリングを考える。
・各ジョブは機械1→機械2の順番で処理される。
・各ジョブが、ある機械から別の機械に移動する時間は0とする。
(すなわちある機械に既に次のジョブが到着してる場合、今処理してるジョブを処理し終わったらすぐに次のジョブを処理することができる。)
・ブロッキングは考えない。
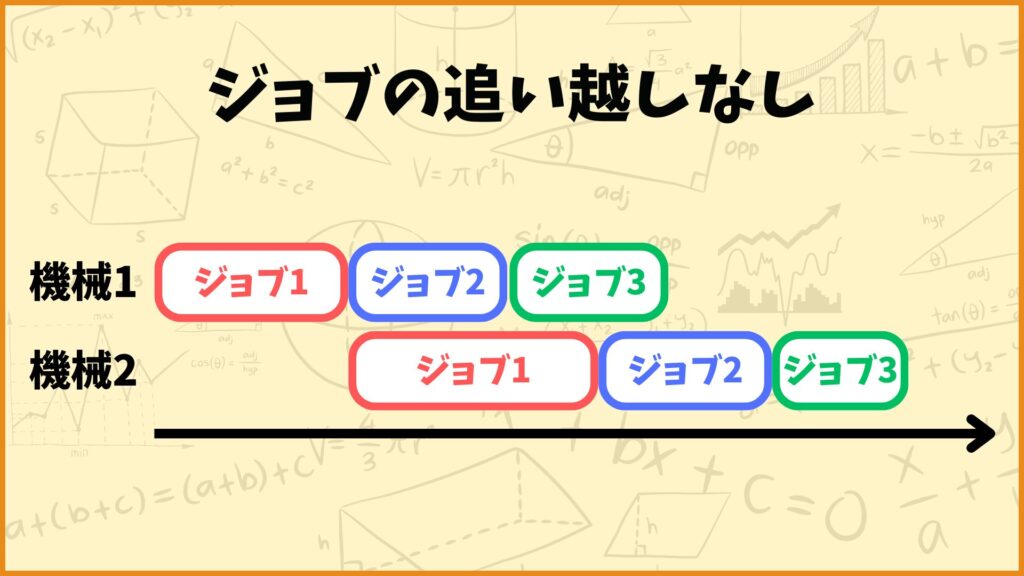
・ジョブの追い越しは考えない。(順列フローショップを考える。)
・機械\(i\)でジョブ\(j\)を処理する時間は\(p_{ij}\)で与えられる。
目的:
全てのジョブを処理し終わるまでの時間が最小となるようなジョブの順番を求める。
「フローショップ・スケジューリング」と「ブロッキング」と「ジョブの追い越し」が何を表すのか、そして具体例を使ってどんな問題を解かないといけないのかを考えてみます。
フローショップ・スケジューリングってなに?
フローショップ・スケジューリング:
・各ジョブは全ての機械それぞれに処理されなければならない。
・全てのジョブは同じ機械の順番で処理される。
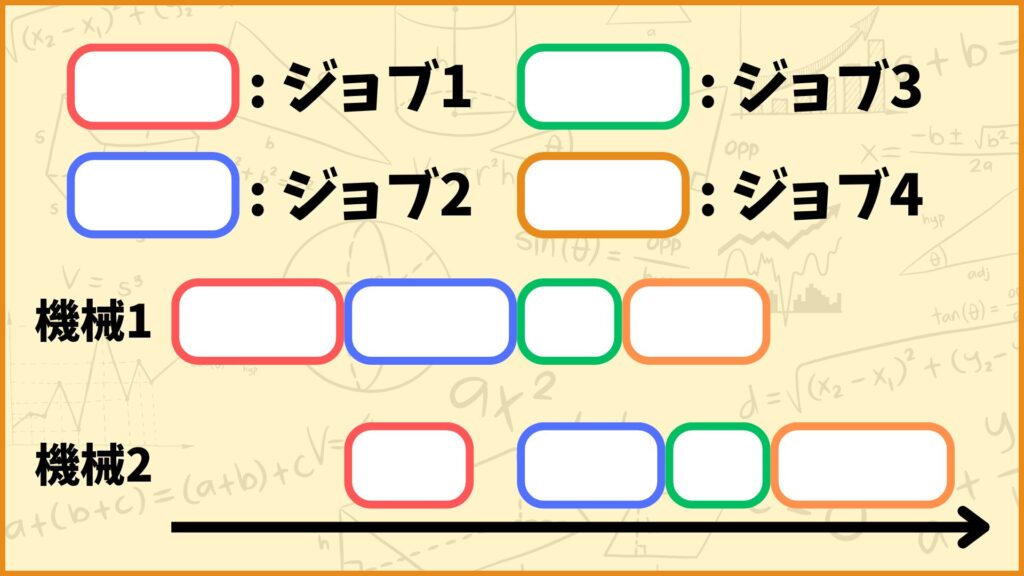
例えば3台の機械で4つのジョブを処理することを考えてみましょう。フローショップでは全てのジョブが同じ機械の順番で処理されます。
例えばジョブ1が機械1→機械2→機械3の順番で処理されるとします。このときジョブ2もジョブ3もジョブ4も全部機械1→機械2→機械3の順番で処理されます。
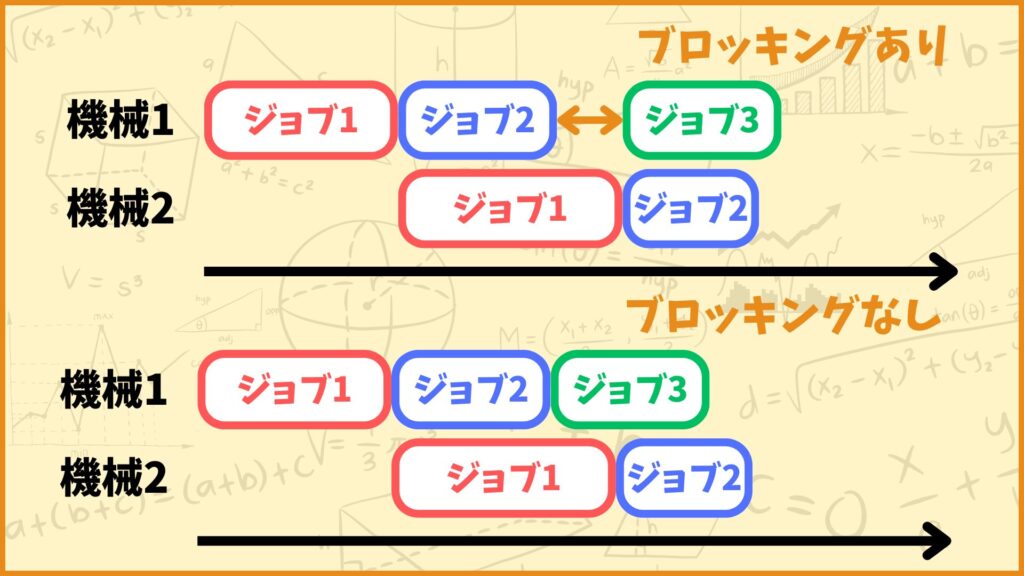
ブロッキングってなに?
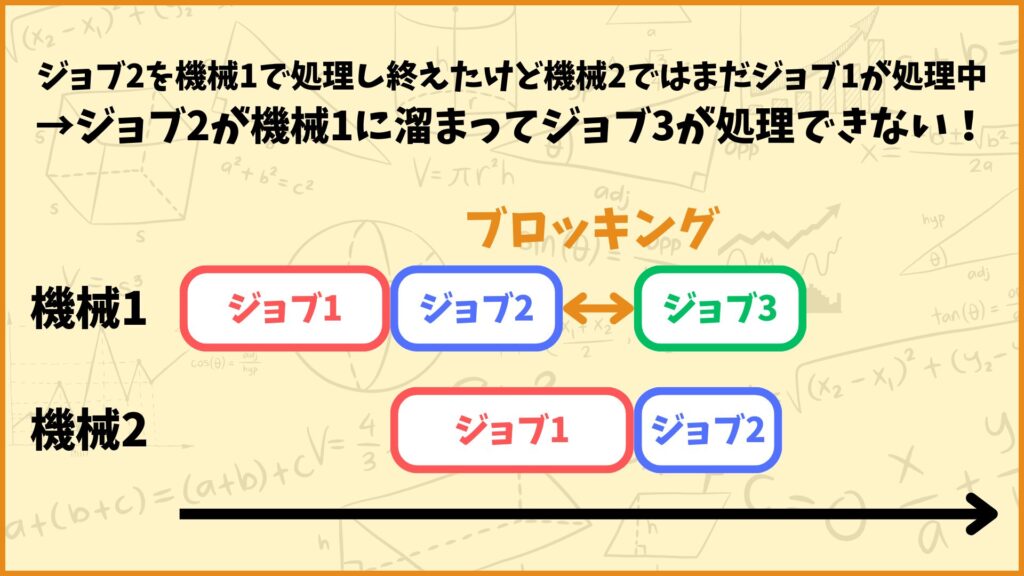
例えば上図を見てみましょう。ジョブ2が機械1で処理し終わった時、機械2ではまだジョブ1を処理中です。このときジョブ2は機械2に移動することができないので機械1にいたままになってしまいます。
そうすると次のジョブであるジョブ3を機械1で処理することができなくなってしまいます。これをブロッキングと言います。
いつジョブ3を機械1で処理し始められるかと言うと、それは機械2でジョブ1を処理し終えた時です。機械2でジョブ1を処理し終えた瞬間ジョブ2が機械1から機械2に移動するので、機械1に処理済みのジョブが溜まることはなくなります。そのためジョブ3を実行できるという訳です。
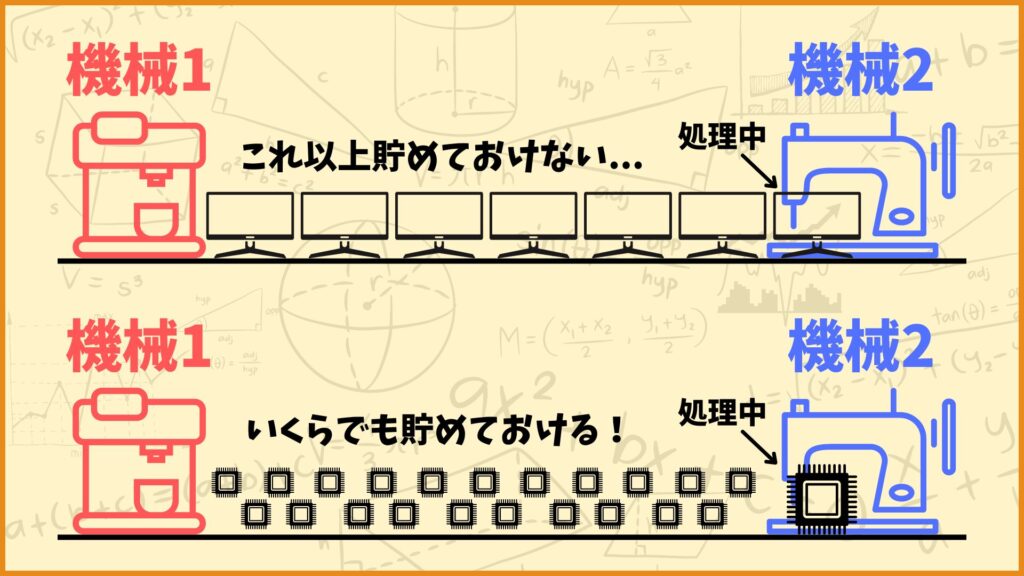
ブロッキングは例えばテレビなどの物理的に大きい物を製造するときに発生します。例えば機械1で処理して得られたテレビのスクリーンを機械2でも処理するとき、機械1と機械2の間でスクリーンを6個までしか貯めておくことができないとします。
そしたら7個目のスクリーンが出来上がった時にそれを置いておく場所がありません。そうなったら機械1に溜まったままになってしまい機械1での作業が止まってしまうというような感じです。
一方で、例えばICチップなど非常に小さい物を製造する際はブロッキングが発生しない場合があります。というのも、小さい物だと実質無限に貯めておけるからです。
今回はブロッキングは発生しないとしてこの先を考えていきます。
ジョブの追い越しってなに?

最後にジョブの追い越しについて説明します。上図の機械1の順番と機械2の順番を見てみると、機械1ではジョブ1→ジョブ2→ジョブ3の順番で処理していますが機械2ではジョブ1→ジョブ3→ジョブ2の順番で処理しています。
これは機械1から機械2の間で、ジョブ3がジョブ2を追い越しているということを表します。今回はこのジョブの追い越しが起こらないようなフローショップを考えていきます。
つまり機械1でジョブ1→ジョブ2→ジョブ3の順番で処理した場合、機械2でもジョブ1→ジョブ2→ジョブ3の順番で処理すると考えます。
このようなフローショップを順列フローショップと言ったりします。
問題例

例えば上の問題例について考えてみましょう。2台の機械で5つのジョブを処理する場合を考えます。各処理時間は上の表のようになっており、例えば機械1がジョブ2を処理する時間は5で、機械2がジョブ4を処理する時間は2です。
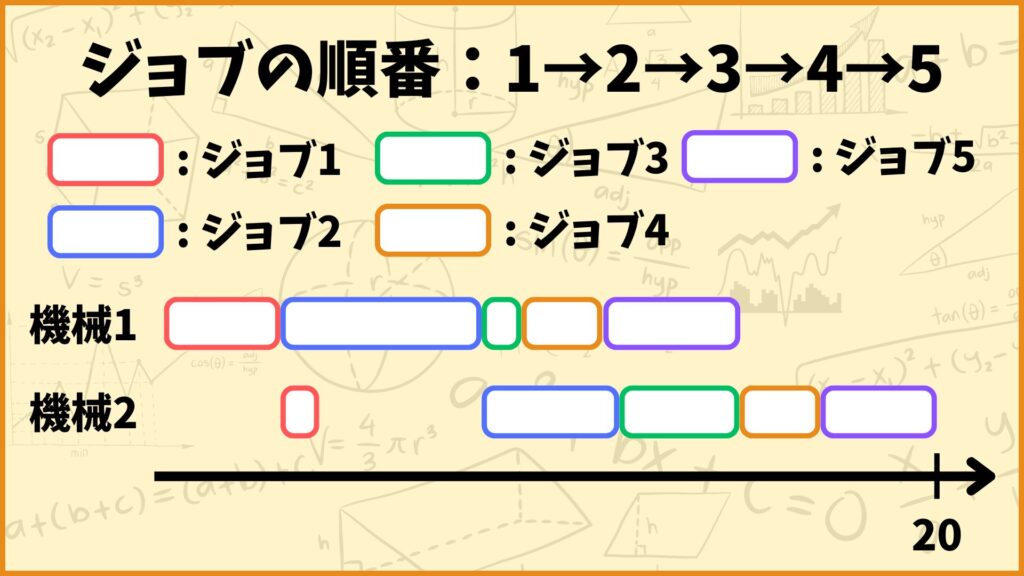
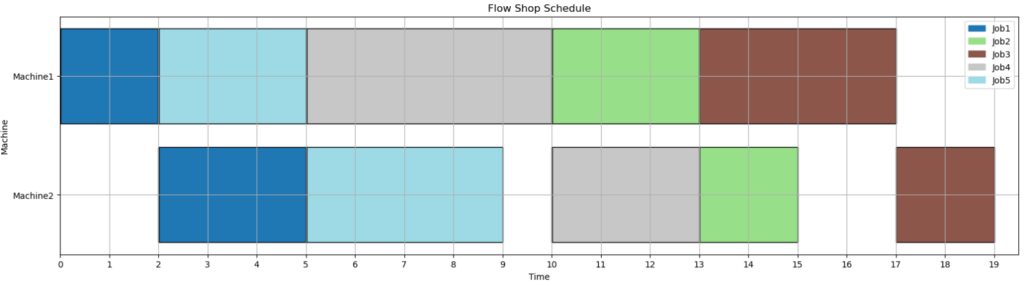
上図はジョブの順番が1→2→3→4→5の場合のスケジュールとなります。この順番の場合、全てのジョブを完了するまでにかかる時間は20となります。
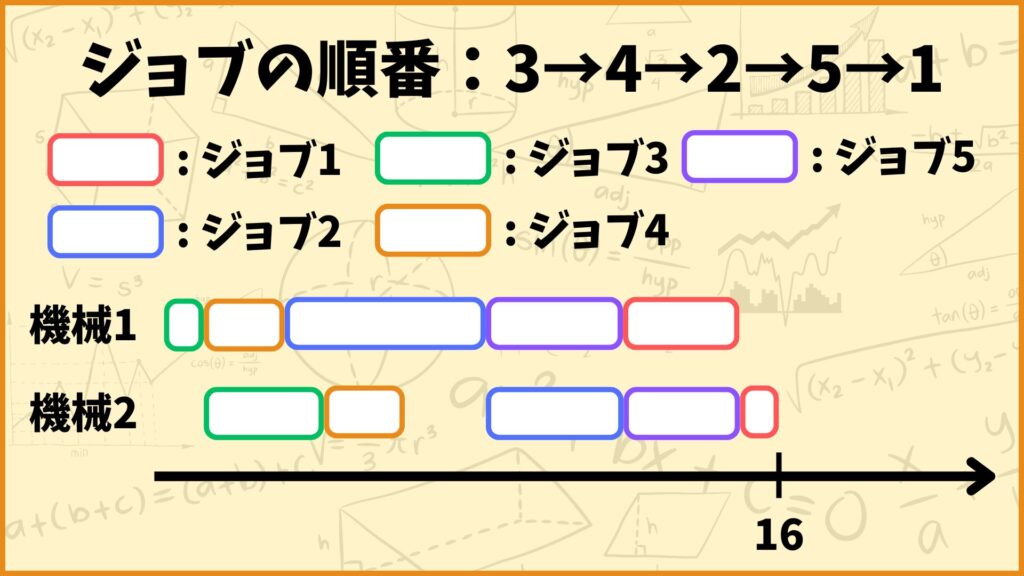
上図はジョブの順番が3→4→2→5→1の場合のスケジュールとなります。この順番の場合、全てのジョブを完了するまでにかかる時間は16となります。こっちの順番の方が早くジョブを終わらせることができますね。
具体例を使ってアルゴリズム(ジョンソン法)を説明する
ここでは機械が2台の場合のフローショップ・スケジューリング問題を解くジョンソン法と言うアルゴリズムの説明をしたいと思います。
ジョンソン法の説明
STEP 1 :
\(p_{1j} < p_{2j}\)となるジョブ\(j\)をGroup1、\(p_{1j} > p_{2j}\)となるジョブ\(j\)をGroup2に入れる。
(\(p_{1j}=p_{2j}\)となるジョブはどっちに入れても良い)
STEP 2 :
Group1のジョブを\(p_{1j}\)が小さい順に並べる。
STEP 3 :
Group2のジョブを\(p_{2j}\)が大きい順に並べてGroup1の後ろにくっつける。
今回の問題の最適解を得るためのアルゴリズムは上記のようになります。文字だけで書かれても何言ってるかよく分からないので具体例を使って解説していきます。
具体例1

上記の問題をこのアルゴリズムを使って解いてみたいと思います。例えば機械1がジョブ4を処理する時間は2ですが、これは
\(p_{14}=2\)
ということを表しています。
STEP 1
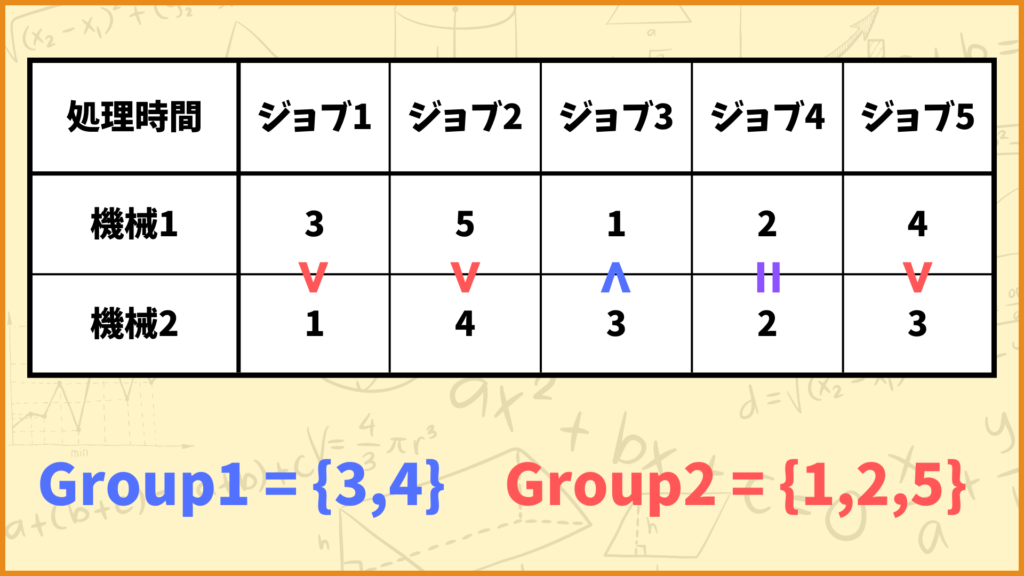
まずSTEP 1ではジョブをグループ分けします。グループの分け方は\(p_{1j} < p_{2j}\)なのか\(p_{1j} > p_{2j}\)なのかで決めます。この式の意味は
「機械1での処理時間の方が小さいジョブはGroup1、機械2での処理時間の方が小さいジョブはGroup2に分ける」
ということです。このように考えるとジョブ3はGroup1、ジョブ1,2,5はGroup2に属すことが分かります。ジョブ4は機械1,2で処理時間が一緒ですが、この場合はどっちのGroupに入れても問題ないです。今回はGroup1に入れました。
STEP 2

STEP 2ではGroup1中のジョブを並べ替えます。どのように並べ替えるかと言うと、
「機械1での処理時間が小さい順」
に並べ替えます。今回の例だと、Group1中のジョブはジョブ3とジョブ4ですが、\(p_{13}=1,p_{14}=2\)なのでジョブ3の方が機械1での処理時間が小さいです。
よってジョブの順番は
ジョブ3→ジョブ4
となります。
STEP 3

STEP 3ではGroup2中のジョブを並べ替えます。どのように並べ替えるかと言うと、
「機械2での処理時間が大きい順」
に並べ替えます。今回の例だと、Group2中のジョブはジョブ1とジョブ2とジョブ5ですが、\(p_{21}=1,p_{22}=4,p_{25}=3\)なので機械2での処理時間が大きい順に並べると
ジョブ2→ジョブ5→ジョブ1
となります。STEP 2で得られたGroup1のジョブ列の後ろにこのジョブの列をくっつけるので最終的に得られるジョブの順番は
ジョブ3→ジョブ4→ジョブ2→ジョブ5→ジョブ1
となります。

具体例2

上記の問題をこのアルゴリズムを使って解いてみたいと思います。例えば機械1がジョブ4を処理する時間は5ですが、これは
\(p_{14}=5\)
ということを表しています。
STEP 1
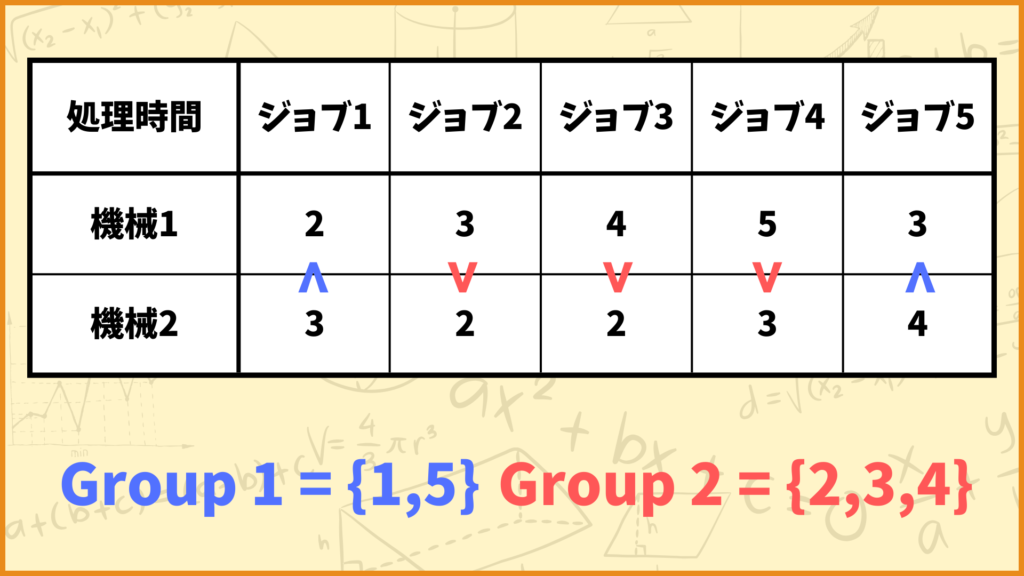
まずSTEP 1ではジョブをグループ分けします。グループの分け方は\(p_{1j} < p_{2j}\)なのか\(p_{1j} > p_{2j}\)なのかで決めます。この式の意味は
「機械1での処理時間の方が小さいジョブはGroup1、機械2での処理時間の方が小さいジョブはGroup2に分ける」
ということです。このように考えるとジョブ1,5はGroup1、ジョブ2,3,4はGroup2に属すことが分かります。
STEP 2

STEP 2ではGroup1中のジョブを並べ替えます。どのように並べ替えるかと言うと、
「機械1での処理時間が小さい順」
に並べ替えます。今回の例だと、Group1中のジョブはジョブ1とジョブ5ですが、\(p_{11}=2,p_{15}=3\)なのでジョブ1の方が機械1での処理時間が小さいです。
よってジョブの順番は
ジョブ1→ジョブ5
となります。
STEP 3

STEP 3ではGroup2中のジョブを並べ替えます。どのように並べ替えるかと言うと、
「機械2での処理時間が大きい順」
に並べ替えます。今回の例だと、Group2中のジョブはジョブ2とジョブ3とジョブ4ですが、\(p_{22}=2,p_{23}=2,p_{24}=3\)なので機械2での処理時間が大きい順に並べると
ジョブ4→ジョブ2→ジョブ3
となります。(ジョブ4→ジョブ3→ジョブ2でもOK)STEP 2で得られたGroup1のジョブ列の後ろにこのジョブの列をくっつけるので最終的に得られるジョブの順番は
ジョブ1→ジョブ5→ジョブ4→ジョブ2→ジョブ3
となります。
pythonで実装してみる
それでは最後に今回紹介したジョンソン法をpythonで実装してみたいと思います。結論以下のコードで問題が解けます。
def two_flowshop(m,p): #引数が「m:ジョブ数、p:処理時間」である関数を定義
Group1 = [] # Group1の初期リスト
Group2 = [] # Group2の初期リスト
p1 = {} # Group1に属すジョブの、機械1での処理時間を記憶しておく辞書(ソートの時に使う)
p2 = {} # Group2に属すジョブの、機械1での処理時間を記憶しておく辞書(ソートの時に使う)
for j in range(m): # 全てのジョブに対して
if p[0][j] <= p[1][j]: # (機械1での処理時間) ≦ (機械2での処理時間)なら
Group1.append(j+1) # Group1にジョブjを追加する(注 : pythonではリストのインデックスが0から始まる)
p1[j+1] = p[0][j] # p1にジョブjの機械1での処理時間を記録しておく
else: #それ以外 ((機械1での処理時間) > (機械2での処理時間))なら
Group2.append(j+1)# Group2にジョブjを追加する(注 : pythonではリストのインデックスが0から始まる)
p2[j+1] = p[1][j] # p2にジョブjの機械2での処理時間を記録しておく
Group1_sorted = sorted(Group1, key=lambda x:p1[x]) # 機械1での処理時間が小さい順にGroup1中のジョブをソートする
Group2_sorted = sorted(Group2, key=lambda x:p2[x], reverse=True) # 機械1での処理時間が大きい順にGroup1中のジョブをソートする
return Group1_sorted+Group2_sorted # 並べ替えた2つのリストを繋げて返す
# 問題例を入力
m = 5 # ジョブ数5
p = [[3,5,1,2,4],[1,4,3,2,3]]
result = two_flowshop(m,p) # 結果をresultに格納
print(f"最適なジョブの順番:{result}") # 結果の表示
このコードを実行したら上のような結果が得られました。それではこのコードが何を表しているか1つずつ解説していきます。
コードの解説
def two_flowshop(m,p): #引数が「m:ジョブ数、p:処理時間」である関数を定義まずdefで今回の問題を解く関数を定義しました。関数名はtwo_flowshop、引数はm,pでそれぞれmがジョブ数、pが処理時間の二次元リストとします。
例えば具体例1の問題を入力したければ
m = 5
p = [[3,5,1,2,4],[1,4,3,2,3]]とすれば良いです。
Group1 = [] # Group1の初期リスト
Group2 = [] # Group2の初期リスト
p1 = {} # Group1に属すジョブの、機械1での処理時間を記憶しておく初期辞書(ソートの時に使う)
p2 = {} # Group2に属すジョブの、機械1での処理時間を記憶しておく辞書(ソートの時に使う)次にGroup1とGroup2の初期リストを生成しています。この後の操作で各ジョブをこれらのリストのいずれかに追加していきます。
その次にp1とp2を設定しています。p1はGroup1に属すジョブの、機械1での処理時間を記憶しておく空辞書でp2はGroup2に属すジョブの、機械1での処理時間を記憶しておく空辞書です。この後の操作で各ジョブの処理時間をp1、p2のいずれかに追加していきます。
これらは後の操作でGroup1,Group2をソートするときに用います。
for j in range(m): # 全てのジョブに対して
if p[0][j] <= p[1][j]: # (機械1での処理時間) ≦ (機械2での処理時間)なら
Group1.append(j+1) # Group1にジョブjを追加する(注 : pythonではリストのインデックスが0から始まる)
p1[j+1] = p[0][j] # p1にジョブjの機械1での処理時間を記録しておく
else: #それ以外 ((機械1での処理時間) > (機械2での処理時間))なら
Group2.append(j+1)# Group2にジョブjを追加する(注 : pythonではリストのインデックスが0から始まる)
p2[j+1] = p[1][j] # p2にジョブjの機械2での処理時間を記録しておく次に各ジョブをGroup1とGroup2にグループ分けします。機械1がジョブjを処理する時間は「p[0][j]」に、機械2がジョブjを処理する時間は「p[1][j]」にそれぞれ格納されているので、これらを比較して「p[0][j]」の方が大きかったらGroup1に、「p[1][j]」の方が大きかったらGroup2に追加しています。
「p[0][j]=p[1][j]」の場合はどっちのグループに入れても問題ないですが、今回はGroup1に入れるように設定しました。
pythonはリストのインデックスが0から始まります。そのため機械1を指定するなら0とする必要があります。またその影響で各グループに追加(append)する要素がjではなくj+1になっています。
またp1ではGroup1に追加されたジョブとそのジョブを機械1で処理する時間を対応づけています。p2ではGroup2に追加されたジョブとそのジョブを機械2で処理する時間を対応づけています。
例えば「p = [[3,5,1,2,4],[1,4,3,2,3]]」の場合「p1 = {3: 1, 4: 2}, p2 = {1: 1, 2: 4, 5: 3}」となるはずです。
Group1_sorted = sorted(Group1, key=lambda x:p1[x]) # 機械1での処理時間が小さい順にGroup1中のジョブをソートする
Group2_sorted = sorted(Group2, key=lambda x:p2[x], reverse=True) # 機械1での処理時間が大きい順にGroup1中のジョブをソートする
return Group1_sorted+Group2_sorted # 並べ替えた2つのリストを繋げて返す
次にGroup1中のジョブを\(p_{1j}\)が小さい順にソートします。リストをソートする場合はsorted()が使えます。先ほど作成したp1を基準にGroup1をソートしたいので()の中身は「Group1, key=lambda x:p1[x]」となっています。
Group2に関してもほぼ同じですが、「reverse = True」とすることで今度は大きい順にソートします。
そして最後にソートしたGroup1_sortedとGroup2_sortedをくっつけて返しています。
# 問題例を入力
m = 5 # ジョブ数5
p = [[3,5,1,2,4],[1,4,3,2,3]]
result = two_flowshop(m,p) # 結果をresultに格納
print(f"最適なジョブの順番:{result}") # 結果の表示
ここからは実際の問題例を入力しています。この入力は具体例1のものになっています。問題の答えはresultに格納され、最後の行でresultを出力しています。

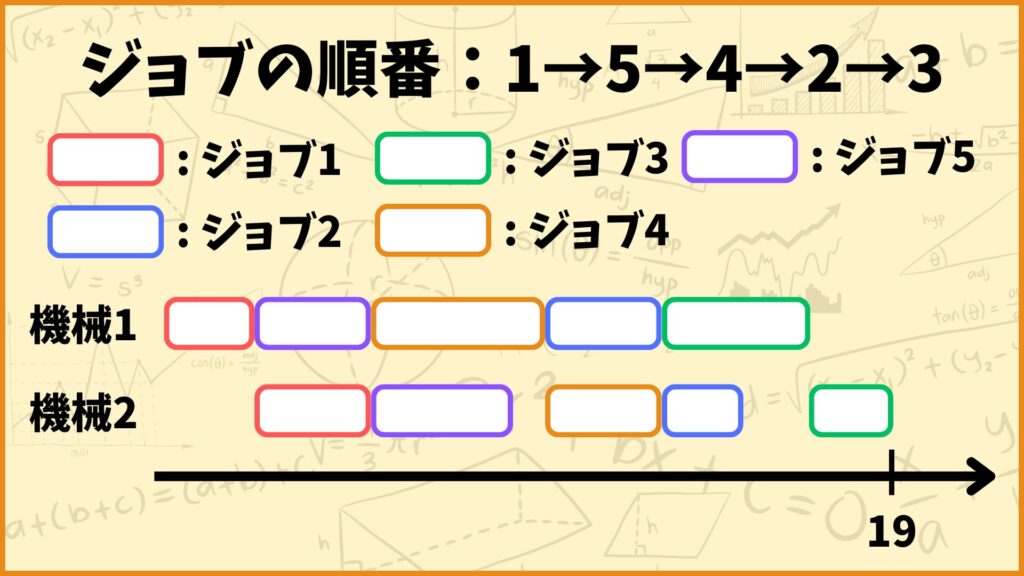
ということで得られた結果がこちらになります。今回の問題例では
ジョブ3→ジョブ4→ジョブ2→ジョブ5→ジョブ1
のスケジュールが、全てのジョブを処理するのにかかる時間が最小となるようなスケジュールとなります。
結果をガントチャートとして描画する
得られた結果をガントチャートとして描画してみましょう。本題ではないのでコードの説明は省略します。
# ライブラリのインポート
import matplotlib.pyplot as plt
import matplotlib.patches as patches
import matplotlib.cm as cm
import numpy as np
# 初期化
jobs = {f'Job{j+1}': {} for j in range(m)}
end_time = [0, 0]
# ジョブの順序に従って処理時間を計算
for job in result:
job_index = job - 1
machine1_start = end_time[0]
machine1_end = machine1_start + p[0][job_index]
jobs[f'Job{job}']['Machine1'] = (machine1_start, machine1_end)
end_time[0] = machine1_end
machine2_start = max(machine1_end, end_time[1])
machine2_end = machine2_start + p[1][job_index]
jobs[f'Job{job}']['Machine2'] = (machine2_start, machine2_end)
end_time[1] = machine2_end
# ジョブごとの色を定義
colors = cm.get_cmap('tab20',m)
job_colors = {f'Job{j+1}': colors(j) for j in range(m)}
# 最大終了時間を計算
max_end_time = max(end for tasks in jobs.values() for start, end in tasks.values())
fig, ax = plt.subplots(1, figsize=(20, 5))
# マシンごとの開始時間と終了時間のバーを描く
machine_y = {'Machine1': 2, 'Machine2': 1}
for job, tasks in jobs.items():
for machine, (start, end) in tasks.items():
ax.add_patch(patches.Rectangle((start, machine_y[machine] - 0.4), end - start, 0.8, edgecolor='black', facecolor=job_colors[job]))
ax.add_patch(patches.Rectangle((start, machine_y[machine] - 0.4), 0.01, 0.8, edgecolor='black', fill=False))
ax.add_patch(patches.Rectangle((end, machine_y[machine] - 0.4), 0.01, 0.8, edgecolor='black', fill=False))
# 凡例の作成
legend_patches = [patches.Patch(color=color, label=job) for job, color in job_colors.items()]
ax.legend(handles=legend_patches, loc='upper right')
# 軸の設定
ax.set_yticks([1, 2])
ax.set_yticklabels(['Machine2', 'Machine1'])
ax.set_xticks(range(int(max_end_time) + 2))
ax.set_xlim(0, max_end_time + 0.5) #
ax.set_xlabel('Time')
ax.set_ylabel('Machine')
ax.set_title('Flow Shop Schedule')
plt.ylim(0.5, 2.5)
plt.grid(True)
plt.show()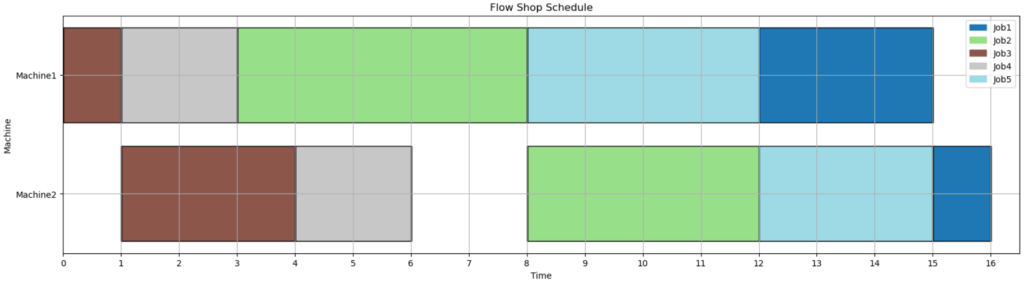
このコードを実行したら上記の図が得られました。具体例2もこれらのコードで解いて結果を見てみましょう。
# 問題例を入力
m = 5 # ジョブ数5
p = [[2,3,4,5,3],[3,2,2,3,4]]
result = two_flowshop(m,p) # 結果をresultに格納
print(f"最適なジョブの順番:{result}") # 結果の表示
色々な問題を解いてみる
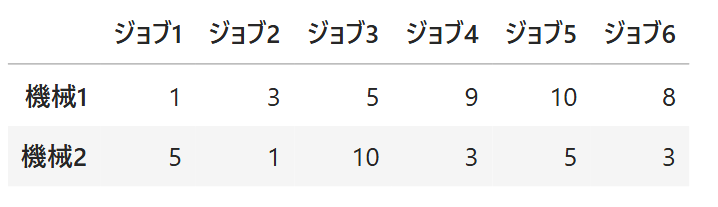
それでは最後に各パラメータ値を色々変えて問題を解いてみたいと思います。
m = 6
処理時間は以下の表の通り
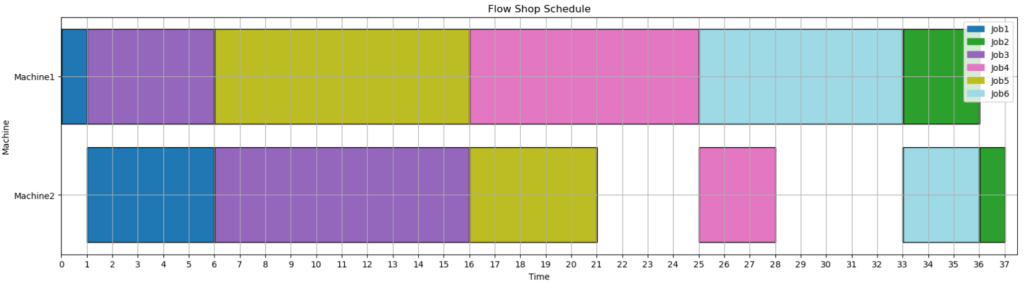
↓↓↓最適なスケジュール↓↓↓
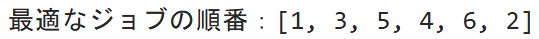
m = 8
処理時間は以下の表の通り
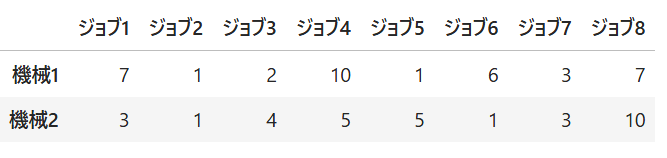
↓↓↓最適なスケジュール↓↓↓
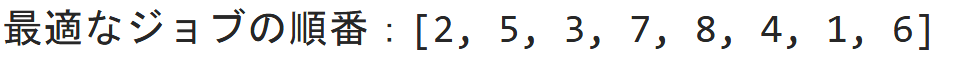
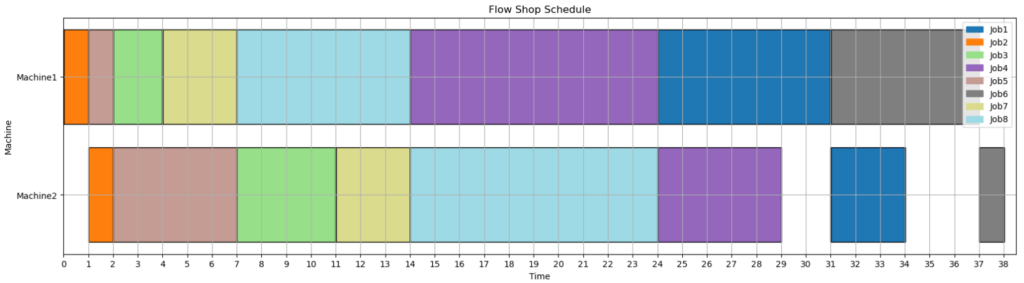
m = 10
処理時間は以下の表の通り

↓↓↓最適なスケジュール↓↓↓
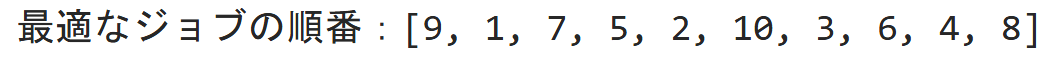
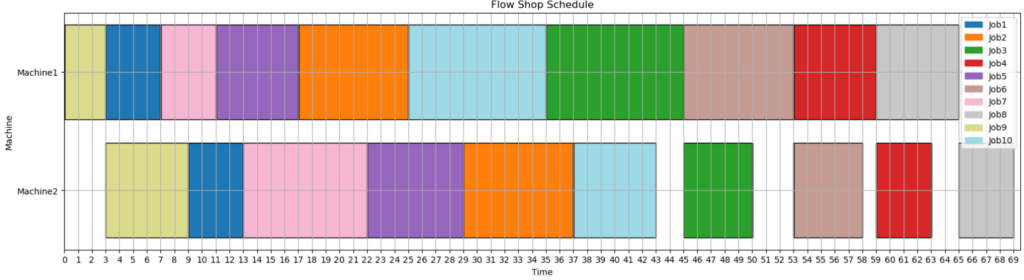
m = 15
処理時間は以下の表の通り

↓↓↓最適なスケジュール↓↓↓
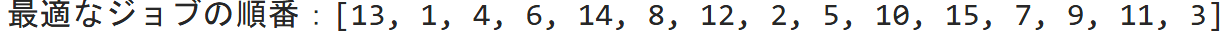
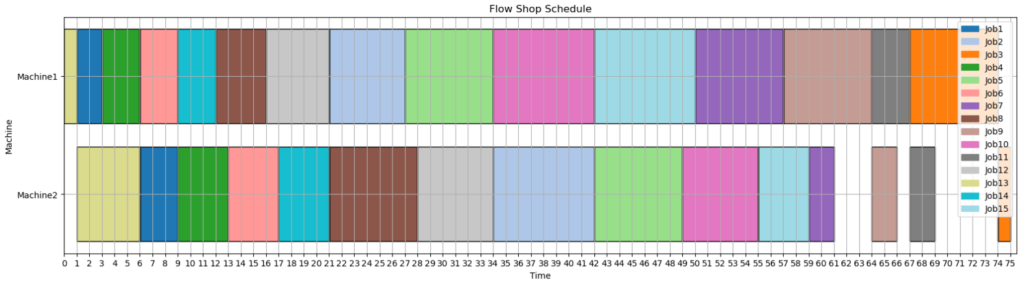
おわりに
いかがでしたか。
今回の記事では機械が2台のフローショップ・スケジューリング問題について解説していきました。
今後もこのような組合せ最適化に関する記事を書いていきます!
最後までこの記事を読んでくれてありがとうございました。



