- 決定木ってなに？
- ジニ不純度ってなに？
- エントロピーってなに？
こんにちは！しゅんです！
今回は決定木で登場するジニ不純度とエントロピーについて解説していきます！
この記事では数式を使ってジニ不純度とエントロピーの解説を行い、次回の記事では決定木をpythonで実装する方法を解説します。
それではやっていきましょう！
普段は組合せ最適化の記事を書いてたりします。
ぜひ他の記事も読んでみてください！
このブログの簡単な紹介はこちらに書いてあります。
興味があったら見てみてください。
このブログでは経営工学を勉強している現役理系大学生が、経営工学に関することを色々話していきます！
ぼくが経営工学を勉強している中で感じたことや、興味深かったことを皆さんと共有出来たら良いなと思っています。
そもそも経営工学とは何なのでしょうか。Wikipediaによると
経営工学（けいえいこうがく、英: engineering management）は、人・材料・装置・情報・エネルギーを総合したシステムの設計・改善・確立に関する活動である。そのシステムから得られる結果を明示し、予測し、評価するために、工学的な分析・設計の原理・方法とともに、数学、物理および社会科学の専門知識と経験を利用する。
引用元 : 経営工学 – Wikipedia
長々と書いてありますが、要は経営、経済の課題を理系的な観点から解決する学問です。
決定木ってなに？
決定木の説明に使う具体例
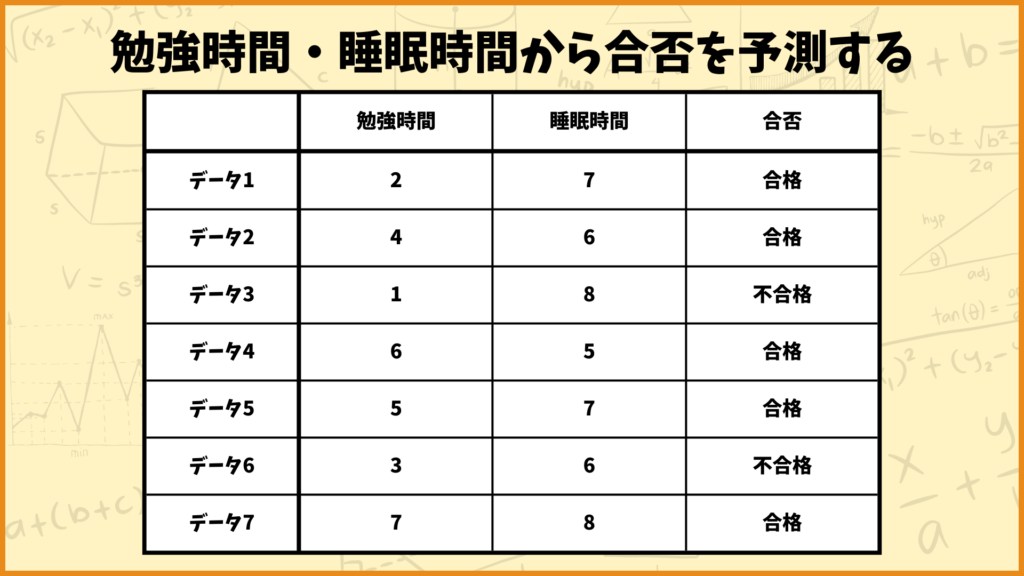
今回は上図の例を使って決定木の説明をしたいと思います。上図の勉強時間データ、睡眠時間データを使って合否を予測することを考えます。
上のデータのように与えられたデータが2つの属性のうちどっちに属すかを予測することを2値分類と言います。一方で例えば与えられたデータがリンゴ、みかん、梨のどれかを予測するなど、3つ以上の属性のうちどれに属すかを予測することを多値分類と言います。
決定木は2値分類も多値分類もできますが、この記事では2値分類を対象に話していきます。
決定木は質問の答えに基づいて予測をしていく
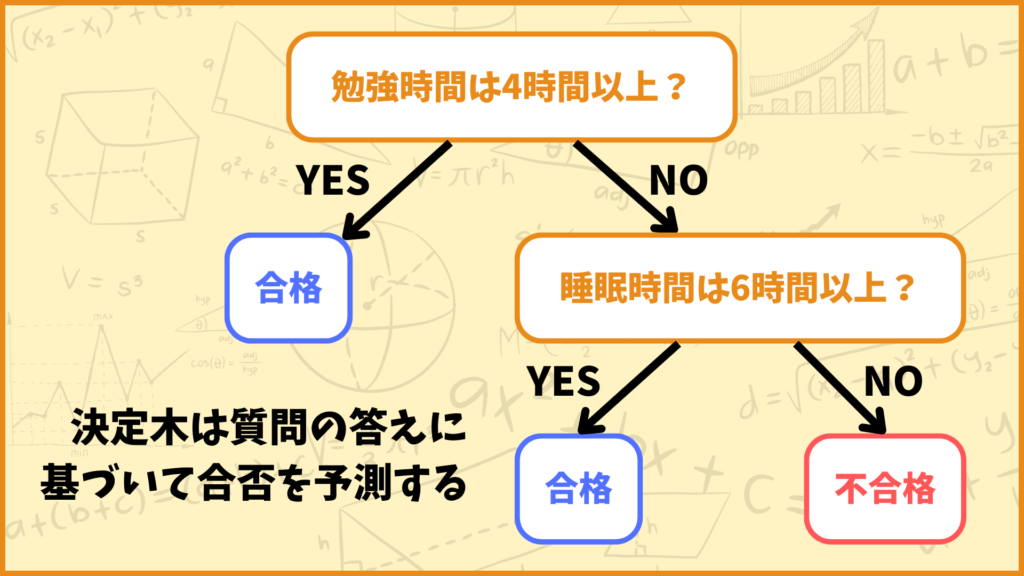
決定木では質問の答えに基づいて合否を予測していきます。上図を見てみましょう。1段階目では「勉強時間は4時間以上かどうか」という質問に対して
YES → 合格
NO → 2段階目の質問に進む
という予測をしています。2段階目では
YES → 合格
NO → 不合格
という予測をしています。これらをまとめると上図の決定木では
合格：
勉強時間が4時間以上、または勉強時間が4時間未満だが睡眠時間が6時間以上
不合格：
勉強時間が4時間未満かつ睡眠時間が6時間未満
という予測をしています。
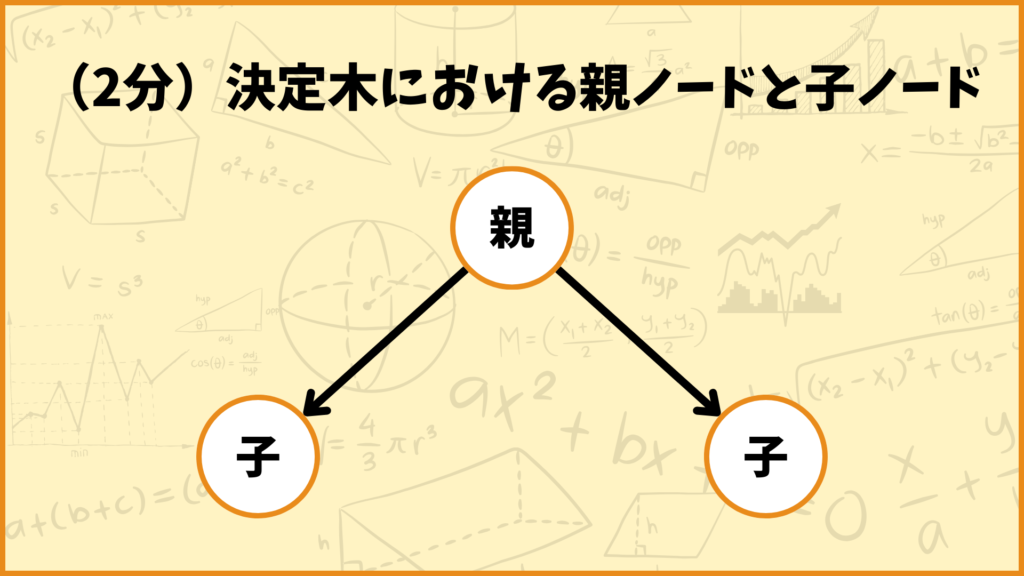
決定木の構造を見ると上図のグラフが2回続いていることが分かります。このような構造を2分決定木と言ったりします。2分決定木のノード（頂点）には親ノードと子ノードという概念があります。
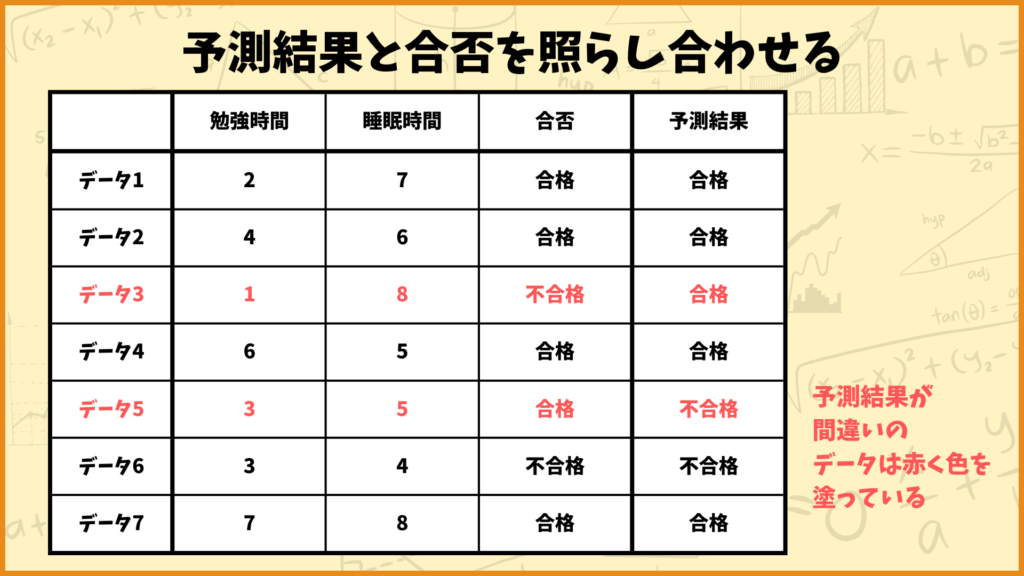
ちなみにこの予測では7個中5個のデータを正しく予測できています。
情報利得が最大となるような質問を考える
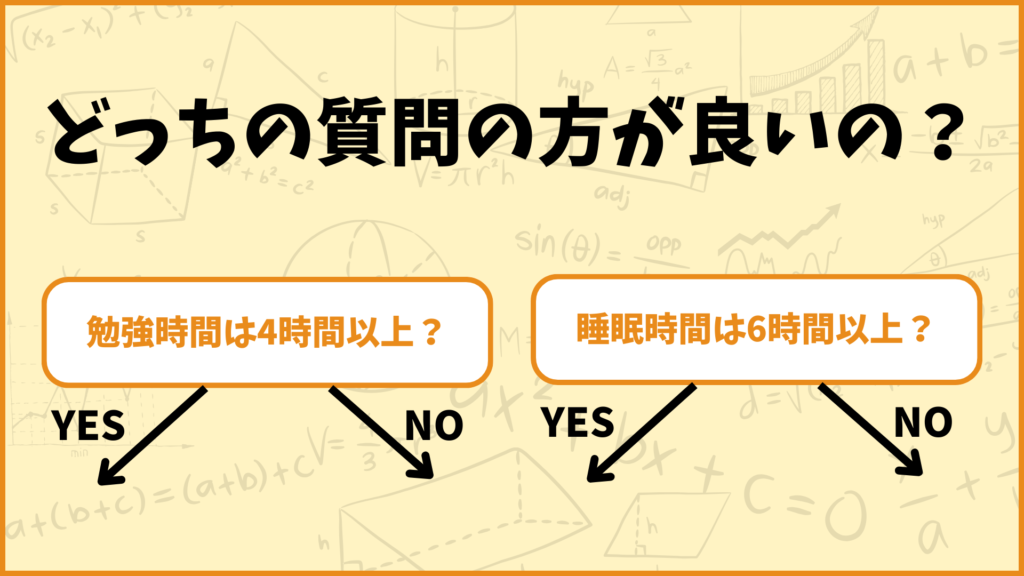
決定木では質問を繰り返して予測を行いますが、どんな質問が良いのでしょうか。上の例で言うと「勉強時間は4時間以上？」という質問と「睡眠時間は6時間以上？」という質問のどっちが良いのでしょうか。
結論、決定木では情報利得が最大となるような質問を考えます。情報利得は以下の式で計算できます。
情報利得 \(IG\) の計算式：
\(IG = I(D_{parent})-\frac{N_{left}}{N_{parent}}I(D_{left})-\frac{N_{right}}{N_{parent}}I(D_{right})\)
\(IG\)：情報利得
\(I(D_{parent})\)：親ノードの不純度
\(I(D_{left})\)：子ノード（左）の不純度
\(I(D_{right})\)：子ノード（右）の不純度
\(N_{parent}\)：親ノードに属すデータ数
\(N_{left}\)：子ノード（左）に属すデータ数
\(N_{right}\)：子ノード（右）に属すデータ数
いきなり文字がたくさん登場してよく分からないので、具体例を使って説明します。
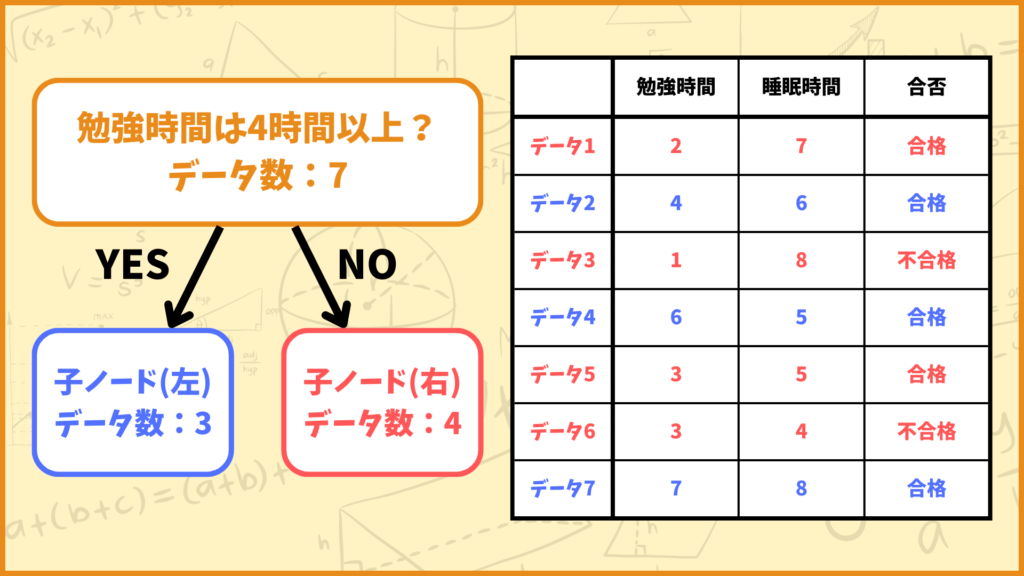
「勉強時間は4時間以上？」という質問について考えます。上図を見ると分かるように、親ノードには7個のデータがあります。この中で、勉強時間が4時間以上のデータは3個、4時間未満のデータは4個あります。
従って左側の子ノードのデータ数は3、右側の子ノードのデータ数は4となります。先ほど登場した文字と照らし合わせると
\(N_{parent} = 7\)
\(N_{left} = 3\)
\(N_{right} = 4\)
となります。従って情報利得の計算式は
\(IG = I(D_{parent})-\frac{3}{7}I(D_{left})-\frac{4}{7}I(D_{right})\)
と表されます。後は \(I(D_{parent}), \; I(D_{left}), \; I(D_{right})\) を計算すれば情報利得が計算できます。これら3つは不純度と呼ばれます。
不純度はそのノードがどれだけ純粋でないかを表しています。不純度の値が小さいほどちゃんと分類できていることを表します。
この不純度を表す指標としてよく使われるのが、ジニ不純度やエントロピーです。
ジニ不純度ってなに？
これまでと同じように勉強時間、睡眠時間と合否の例を使って説明します。
ジニ不純度の計算式
ジニ不純度の計算式：
\(I(D) = 1-p(\text{合格}|D)^2-p(\text{不合格}|D)^2\)
\(p(\text{合格}|D)\)：ノード\(D\)に属す合格データの割合
\(p(\text{不合格}|D)\)：ノード\(D\)に属す不合格データの割合
例えばノード \(D\) に属すデータが100個あり、そのうち40個が合格データ、60個が不合格データの場合
\(p(\text{合格}|D) = \frac{40}{100}\)
\(p(\text{不合格}|D) = \frac{60}{100}\)
となります。従ってノード \(D\) のジニ不純度は
\(I(D) = 1 – (\frac{40}{100})^2 – (\frac{60}{100}) = \frac{12}{25}=0.48\)
と計算できます。
\(p(\text{不合格}|D)\) はノード \(D\) に属す不合格データの割合ですが、これを言い換えるとノード \(D\) に属す合格データでないデータの割合です。従って
\(p(\text{不合格}|D) = 1-p(\text{合格}|D)\)
が成り立ちます。
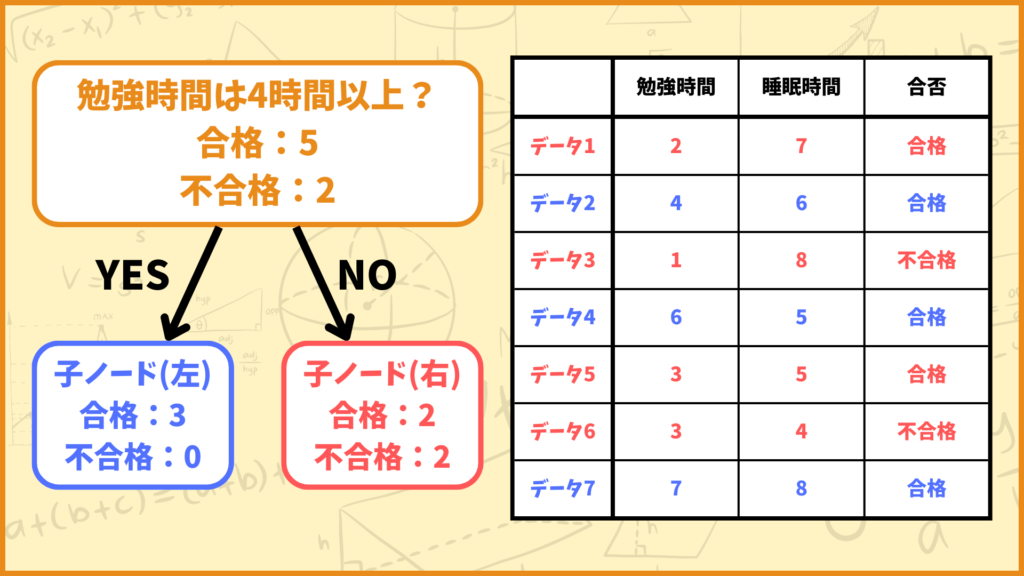
親ノードのジニ不純度
親ノードに属すデータ数は
全体：7個
合格：5個
不合格：2個
となるので
\(p(\text{合格}|D_{parent})=\frac{5}{7}\)
\(p(\text{不合格}|D_{parent})=\frac{2}{7}\)
となります。従って親ノードのジニ不純度は
\(I(D_{parent})=1-(\frac{5}{7})^2-(\frac{2}{7})^2=\frac{20}{49}\)
と計算できます。
子ノード（左）のジニ不純度
左側の子ノードに属すデータ数は
全体：3個
合格：3個
不合格：0個
となるので
\(p(\text{合格}|D_{left})=\frac{3}{3}=1\)
\(p(\text{不合格}|D_{left})=\frac{0}{3}=0\)
となります。従って左側の子ノードのジニ不純度は
\(I(D_{left})=1-1^2-0^2=0\)
と計算できます。
子ノード（右）のジニ不純度
右側の子ノードに属すデータ数は
全体：4個
合格：2個
不合格：2個
となるので
\(p(\text{合格}|D_{right})=\frac{2}{4}\)
\(p(\text{不合格}|D_{right})=\frac{2}{4}\)
となります。従って右側の子ノードのジニ不純度は
\(I(D_{right})=1-(\frac{2}{4})^2-(\frac{2}{4})^2=\frac{1}{2}\)
と計算できます。
ジニ不純度を使って情報利得を計算する
ここまでの話で
\(I(D_{parent}) = \frac{20}{49}\)
\(I(D_{left}) = 0\)
\(I(D_{right}) = \frac{1}{2}\)
ということが分かりました。従って情報利得は
\(IG = I(D_{parent})-\frac{3}{7}I(D_{left})-\frac{4}{7}I(D_{right})\)
\(= \frac{20}{49}-\frac{3}{7}\times 0-\frac{4}{7}\times\frac{1}{2}\)
\(=\frac{6}{49}≒0.12\)
と計算できます。
エントロピーってなに？
これも勉強時間、睡眠時間と合否の例を使って説明します。
エントロピーの計算式
エントロピーの計算式：
\(I(D) = -p(\text{合格}|D)\log_2p(\text{合格}|D)\)
\(-p(\text{不合格}|D)\log_2p(\text{不合格}|D)\)
\(p(\text{合格}|D)\)：ノード\(D\)に属す合格データの割合
\(p(\text{不合格}|D)\)：ノード\(D\)に属す不合格データの割合
\(p(\text{合格}|D),\; p(\text{不合格}|D)\) はジニ不純度のときと同じ定義です。例えばノード \(D\) に属すデータが100個あり、そのうち40個が合格データ、60個が不合格データの場合
\(p(\text{合格}|D) = \frac{40}{100}\)
\(p(\text{不合格}|D) = \frac{60}{100}\)
となります。従ってノード \(D\) のエントロピーは
\(I(D) = -\frac{40}{100}\log_2\frac{40}{100}-\frac{60}{100}\log_2\frac{60}{100} ≒ 0.97\)
と計算できます。
親ノードのエントロピー
親ノードに属すデータ数は
全体：7個
合格：5個
不合格：2個
となるので
\(p(\text{合格}|D_{parent})=\frac{5}{7}\)
\(p(\text{不合格}|D_{parent})=\frac{2}{7}\)
となります。従って親ノードのエントロピーは
\(I(D_{parent})=-\frac{5}{7}\log_2\frac{5}{7}-\frac{2}{7}\log_2\frac{2}{7}≒0.86\)
と計算できます。
子ノード（左）のエントロピー
左側の子ノードに属すデータ数は
全体：3個
合格：3個
不合格：0個
となるので
\(p(\text{合格}|D_{left})=\frac{3}{3}=1\)
\(p(\text{不合格}|D_{left})=\frac{0}{3}=0\)
となります。従って左側の子ノードのエントロピーは
\(I(D_{left})=-1\times\log_21-0\times\log_20=0\)
と計算できます。但し\(0\times\log_20=0\)とします。
子ノード（右）のエントロピー
右側の子ノードに属すデータ数は
全体：4個
合格：2個
不合格：2個
となるので
\(p(\text{合格}|D_{right})=\frac{2}{4}\)
\(p(\text{不合格}|D_{right})=\frac{2}{4}\)
となります。従って右側の子ノードのジニ不純度は
\(I(D_{right})=-\frac{2}{4}\log_2\frac{2}{4}-\frac{2}{4}\log_2\frac{2}{4}=1\)
と計算できます。
エントロピーを使って情報利得を計算する
ここまでの話で
\(I(D_{parent}) = 0.86\)
\(I(D_{left}) = 0\)
\(I(D_{right}) = 1\)
ということが分かりました。従って情報利得は
\(IG = 0.86-\frac{3}{7}\times 0-\frac{4}{7}\times 1=0.29\)
と計算できます。
質問を変えて情報利得を計算する
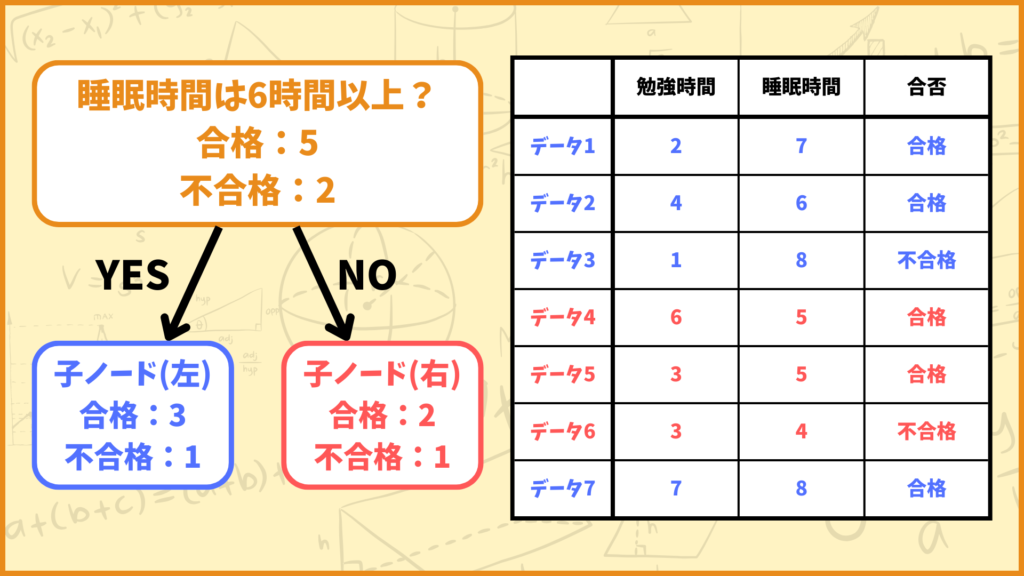
それでは次に質問を
「睡眠時間は6時間以上？」
という質問に変えて情報利得を計算してみましょう。なお計算の手順は同じなの途中式は省略します。
ジニ不純度を使って情報利得を計算する
\(I(D_{parent}) = \frac{20}{49}\)
\(I(D_{left}) = \frac{3}{8}\)
\(I(D_{right}) = \frac{4}{9}\)
と計算されます。従って情報利得は
\(IG = \frac{20}{49}-\frac{4}{7}\times\frac{3}{8}-\frac{3}{7}\times\frac{4}{9}≒0.0034\)
と計算できます。
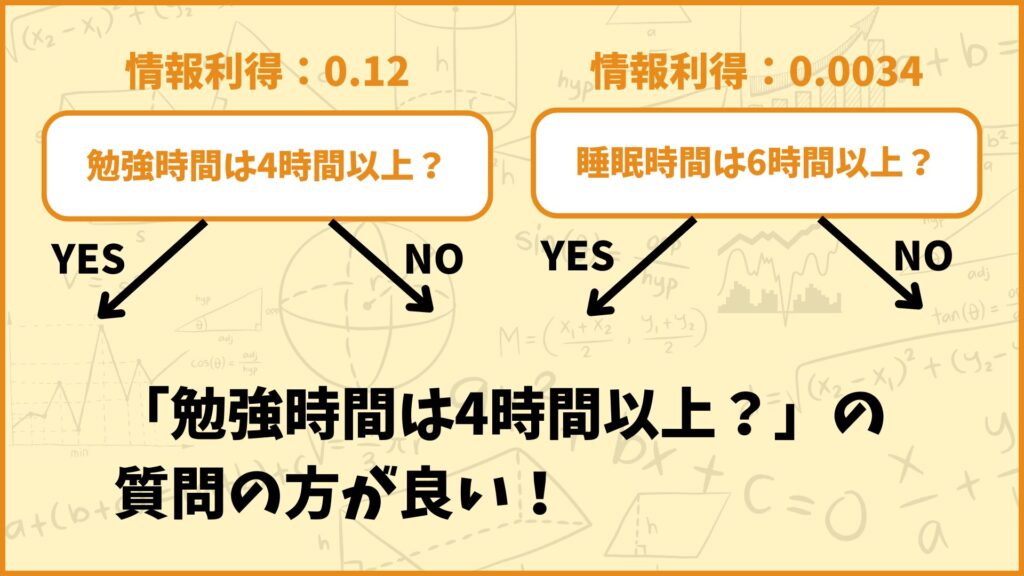
ということでジニ不純度から計算された情報利得を比べると
「勉強時間は4時間以上？」
の質問の方が良いことが分かりました。
エントロピーを使って情報利得を計算する
\(I(D_{parent}) ≒ 0.86\)
\(I(D_{left}) ≒ 0.81\)
\(I(D_{right}) ≒ 0.92\)
と計算されます。従って情報利得は
\(IG = 0.86-\frac{4}{7}\times 0.81-\frac{3}{7}\times 0.92≒0.0060\)
と計算できます。
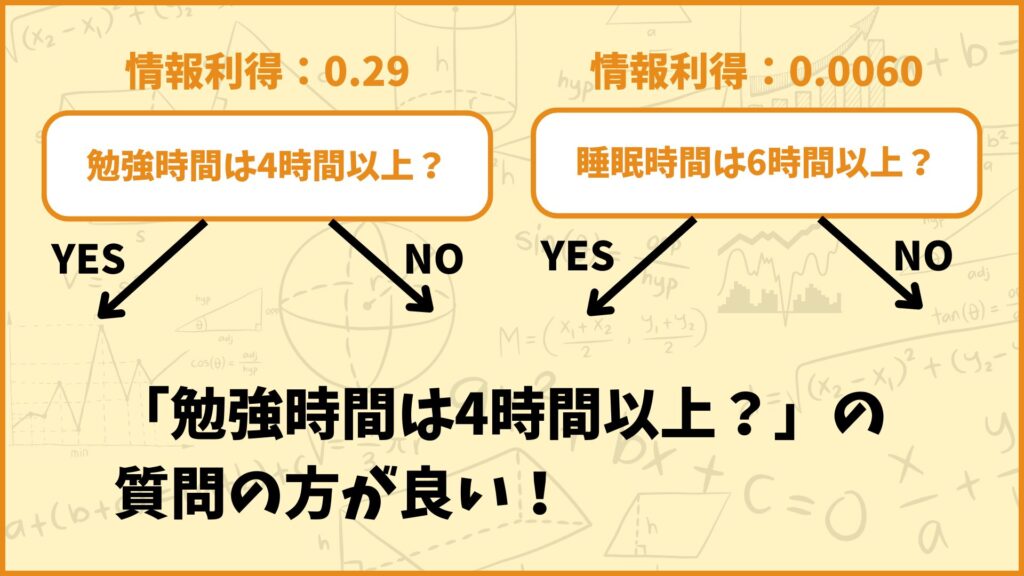
ということでエントロピーから計算された情報利得を比べても
「勉強時間は4時間以上？」
の質問の方が良いことが分かりました。
ジニ不純度とエントロピーを図示する
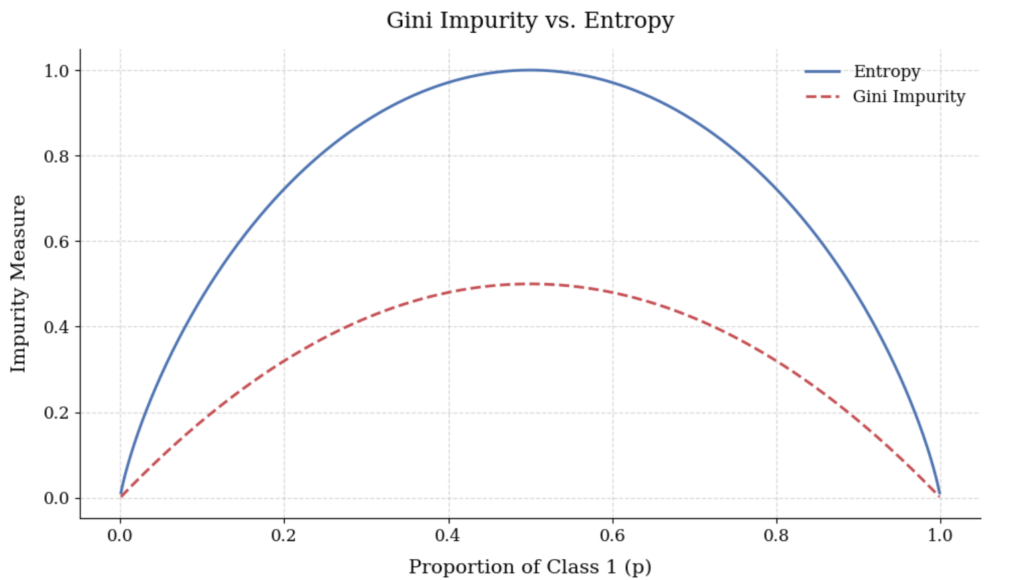
最後にジニ不純度とエントロピーを図示してみました。縦軸はそれぞれの値、横軸はクラス1に属すデータの割合を表しています。今回の例で言えば横軸は \(p(\text{合格}|D)\) を表しています。
これを見るとジニ不純度もエントロピーも同じような形をしていますね。
おわりに
いかがでしたか。
今回の記事ではジニ不純度とエントロピーについて解説しました。
今後もこのような機械学習に関する記事を書いていきます！
最後までこの記事を読んでくれてありがとうございました。
参考文献
