こんにちは!しゅんです!
今回の記事では前回説明したナップサック問題の制約条件を色々変更して答えがどうなるかを調べてみました!
前回のナップサック問題の記事はこちらから見れます!
また変更した制約条件を数式で表して、pythonを使って実装してみたいと思います。
それでは解説していきましょう!
普段は統計検定2級の記事を書いてたりします。
ぜひ他の記事も読んでみてください!
このブログの簡単な紹介はこちらに書いてあります。
興味があったら見てみてください。
このブログでは経営工学を勉強している現役理系大学生が、経営工学に関することを色々話していきます!
ぼくが経営工学を勉強している中で感じたことや、興味深かったことを皆さんと共有出来たら良いなと思っています。
そもそも経営工学とは何なのでしょうか。Wikipediaによると
経営工学(けいえいこうがく、英: engineering management)は、人・材料・装置・情報・エネルギーを総合したシステムの設計・改善・確立に関する活動である。そのシステムから得られる結果を明示し、予測し、評価するために、工学的な分析・設計の原理・方法とともに、数学、物理および社会科学の専門知識と経験を利用する。
引用元 : 経営工学 – Wikipedia
長々と書いてありますが、要は経営、経済の課題を理系的な観点から解決する学問です。
デフォルトの問題を設定する
制約条件を色々変更する前にまずはデフォルトのナップサック問題を設定します。前回の記事と一緒なので説明は飛ばします。
今回扱う問題
・遠足に持っていくお菓子を決める。
・20個のお菓子の中から持っていくものを選ぶ。
・合計300円までしかお菓子を持っていけない。
・同じお菓子は1つまでしか持っていけない。
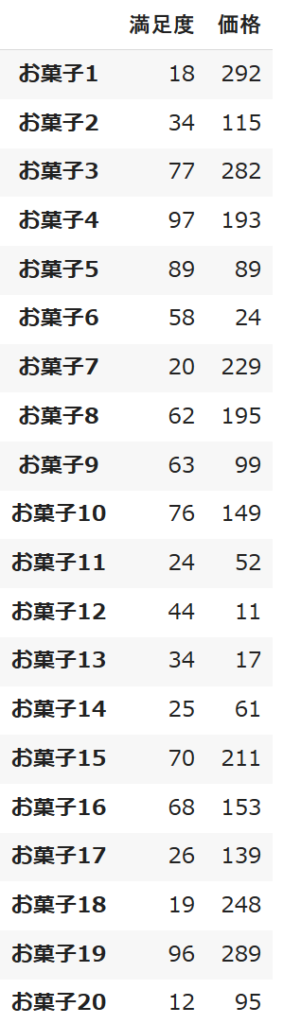
・お菓子1つ1つに値段と満足度が割り当てられている。

\(\text{max}\;\;\sum\limits^{20}_{i=1}v_ix_i\)
\(\text{s.t.}\;\;\;\;\sum\limits^{20}_{i=1}w_ix_i \leq 300\)
\(\;\;\;\;\;\;\;\;\;\;x_i \in \{0,1\} \;\;\;\;\;\;\;\;\;(i=1,2,…,20) \)
但し\(v_i\)はお菓子\(i\)の満足度、\(w_i\)はお菓子\(i\)の値段を表す。
この問題は以下のようにpythonで実装することができ、結果が得られます。
## ナップサック問題を解くための前準備
# pulpをインポート
! pip install pulp
from pulp import *
# pandasをインポート
import pandas as pd
# numpyをインポート
import numpy as np
# 満足度vをランダムに設定
np.random.seed(100)
v = np.random.randint(10, 100, 20)
# 値段wをランダムに設定
np.random.seed(200)
w = np.random.randint(10, 300, 20)
# 予算の上限を設定
capacity = 300
## ナップサック問題を設定して実際に解いてみる
# LpMaximizeで最大化に設定
prob = LpProblem(sense=LpMaximize)
# 変数の定義(まとめて定義)
x = [LpVariable(f"x{i}", cat = LpBinary) for i in range(1,21)]
# 問題の設定
prob += lpDot(v, x) # 目的関数を設定
prob += lpDot(w, x) <= capacity # 制約条件を設定
prob.solve() # 問題を解く
# 結果を表示
print(LpStatus[prob.status]) # 解の状態を表示(Optimalなら最適解が求められている)
print("Optimal Value =", value(prob.objective)) # 最適値を表示
for x in prob.variables():
print(x,"=", value(x)) # 最適解を表示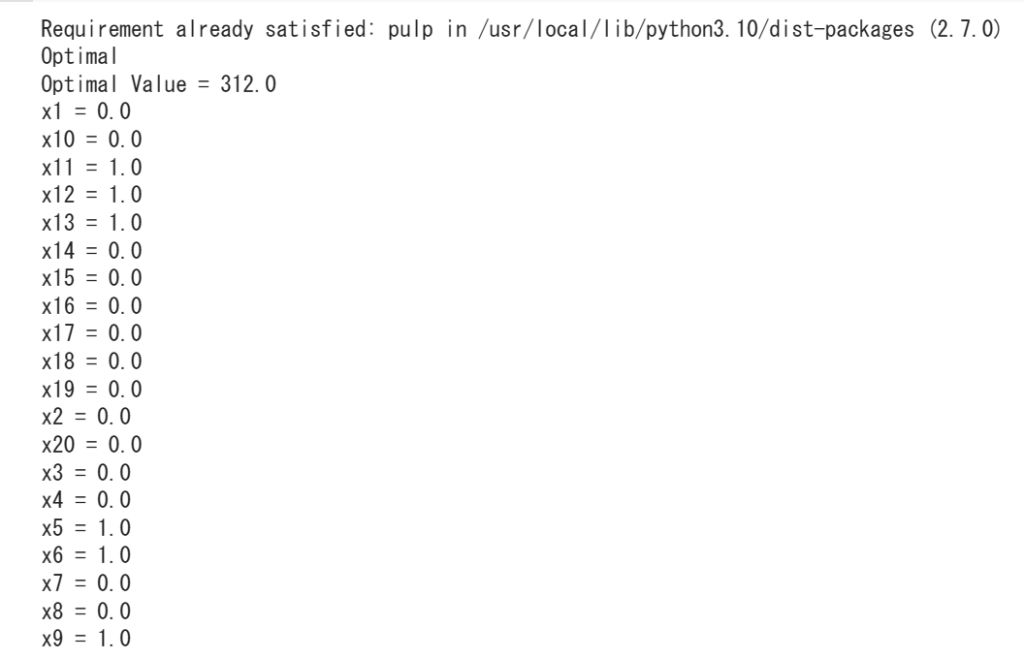
それではここから制約条件を色々変えてみましょう。
制約条件を変えてみる
値段の上限を400円にする
まずは値段の上限を300円から400円に変えてみましょう。これは非常に簡単でcapacityの300の所を400に変えるだけでOKです。
\(\text{max}\;\;\sum\limits^{20}_{i=1}v_ix_i\)
\(\text{s.t.}\;\;\;\;\sum\limits^{20}_{i=1}w_ix_i \leq 400\)
\(\;\;\;\;\;\;\;\;\;\;x_i \in \{0,1\} \;\;\;\;\;\;\;\;\;(i=1,2,…,20) \)
但し\(v_i\)はお菓子\(i\)の満足度、\(w_i\)はお菓子\(i\)の値段を表す。
これをpythonで実装すると以下のようになります。
## ナップサック問題を解くための前準備
# pulpをインポート
! pip install pulp
from pulp import *
# pandasをインポート
import pandas as pd
# numpyをインポート
import numpy as np
# 満足度vをランダムに設定
np.random.seed(100)
v = np.random.randint(10, 100, 20)
# 価格wをランダムに設定
np.random.seed(200)
w = np.random.randint(10, 300, 20)
# 予算の上限を設定 ←ここを400に変更する!!!!!!!!!!!!!!!!!
capacity = 400
## ナップサック問題を設定して実際に解いてみる
# LpMaximizeで最大化に設定
prob = LpProblem(sense=LpMaximize)
# 変数の定義(まとめて定義)
x = [LpVariable(f"x{i}", cat = LpBinary) for i in range(1,21)]
# 問題の設定
prob += lpDot(v, x) # 目的関数を設定
prob += lpDot(w, x) <= capacity # 制約条件を設定
prob.solve() # 問題を解く
# 結果を表示
print(LpStatus[prob.status]) # 解の状態を表示(Optimalなら最適解が求められている)
print("Optimal Value =", value(prob.objective)) # 最適値を表示
for x in prob.variables():
print(x,"=", value(x)) # 最適解を表示
制約条件変えた場合の最適解

元の問題の最適解
左が上限を400円にしたときの出力結果で、右が元の問題の出力結果です。これを見るとx10とx11の値が変わっていることが分かります。
お菓子10の満足度は76と高めですがその分価格も149と少し高めなことが分かります。そのため300円の予算だと選択されなかったのに400円まで予算を増やすと選択されたんですね。
予算制約を1000円、2000円に増やしていくとどうなるか考えるのも面白そうですね。
2個以上買っても良いことにする
次に個数の制約を変えてみましょう。変数\(x_i\)は0-1変数として設定していたので1つのお菓子を最大でも1個までしか選ぶことができませんでした。ここを変更して、2個以上買ってもよいことにしてみます。
\(x_i \in \{0,1\}\)の制約を0以上の整数にしましょう。定式化すると以下のようになります。
\(\text{max}\;\;\sum\limits^{20}_{i=1}v_ix_i\)
\(\text{s.t.}\;\;\;\;\sum\limits^{20}_{i=1}w_ix_i \leq 300\)
\(\;\;\;\;\;\;\;\;\;\;x_i \in \mathbb{Z} \;\;\;\;\;\;\;\;\;(i=1,2,…,20)\)
\(\;\;\;\;\;\;\;\;\;\;x_i \geq 0 \;\;\;\;\;\;\;\;\;(i=1,2,…,20) \)
但し\(v_i\)はお菓子\(i\)の満足度、\(w_i\)はお菓子\(i\)の値段を表す。
\(\mathbb{Z}\)は整数全体を表しています。これだけだとマイナスの値も取りうるので\(x_i \geq 0\)の制約も入れています。
これをpythonで表すと以下のようになります。25行目のcatの所をLpBinaryからLpIntegerに変えて、31~32行目ですべての\(i\)に対して\(x_i \geq 0\)となるように設定しています。
## ナップサック問題を解くための前準備
# pulpをインポート
! pip install pulp
from pulp import *
# pandasをインポート
import pandas as pd
# numpyをインポート
import numpy as np
# 満足度vをランダムに設定
np.random.seed(100)
v = np.random.randint(10, 100, 20)
# 価格wをランダムに設定
np.random.seed(200)
w = np.random.randint(10, 300, 20)
# 予算の上限を設定
capacity = 300
## ナップサック問題を設定して実際に解いてみる
# LpMaximizeで最大化に設定
prob = LpProblem(sense=LpMaximize)
# 変数の定義(まとめて定義)ここを変更する!!!!!!!!!!!!!!!!!!!!
x = [LpVariable(f"x{i}", cat = LpInteger) for i in range(1,21)]
# 問題の設定
prob += lpDot(v, x) # 目的関数を設定
prob += lpDot(w, x) <= capacity # 制約条件を設定
# ここを変更する!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!
for i in range(len(x)):
prob += x[i] >= 0
prob.solve() # 問題を解く
# 結果を表示
print(LpStatus[prob.status]) # 解の状態を表示(Optimalなら最適解が求められている)
print("Optimal Value =", value(prob.objective)) # 最適値を表示
for x in prob.variables():
print(x,"=", value(x)) # 最適解を表示
制約条件変えた場合の最適解

元の問題の最適解
これを見るとお菓子12を21個選ぶのが最適解になっていますね。確かにお菓子12は満足度44、価格11と非常にコスパが良いお菓子になっています。たださすがに同じお菓子を21個買うのは現実的ではないですよね。
これの解決策として例えば最大3個までしか買えないという制約を加えたり、2個目からは満足度が減少するように設定することが考えられます。
3個までしか買えないことにする
1個までしか買えないという制約を3個までしか買えないという制約に変えます。1個前の話では変数\(x_i\)を整数に設定して\(x_i \geq 0\)の制約を追加しましたが、さらにそこに\(x_i \leq 3\)の制約を追加すればOKです。
\(\text{max}\;\;\sum\limits^{20}_{i=1}v_ix_i\)
\(\text{s.t.}\;\;\;\;\sum\limits^{20}_{i=1}w_ix_i \leq 300\)
\(\;\;\;\;\;\;\;\;\;\;x_i \in \mathbb{Z} \;\;\;\;\;\;\;\;\;(i=1,2,…,20)\)
\(\;\;\;\;\;\;\;\;\;\;0 \leq x_i \leq 3 \;\;\;(i=1,2,…,20) \)
但し\(v_i\)はお菓子\(i\)の満足度、\(w_i\)はお菓子\(i\)の値段を表す。
これをpythonで表すと以下のようになります。
## ナップサック問題を解くための前準備
# pulpをインポート
! pip install pulp
from pulp import *
# pandasをインポート
import pandas as pd
# numpyをインポート
import numpy as np
# 満足度vをランダムに設定
np.random.seed(100)
v = np.random.randint(10, 100, 20)
# 価格wをランダムに設定
np.random.seed(200)
w = np.random.randint(10, 300, 20)
# 予算の上限を設定
capacity = 300
## ナップサック問題を設定して実際に解いてみる
# LpMaximizeで最大化に設定
prob = LpProblem(sense=LpMaximize)
# 変数の定義(まとめて定義)
x = [LpVariable(f"x{i}", cat = LpInteger) for i in range(1,21)]
# 問題の設定
prob += lpDot(v, x) # 目的関数を設定
prob += lpDot(w, x) <= capacity # 制約条件を設定
# ここを変更する!!!!!!!!!!!!!!!!!!!!!
for i in range(len(x)):
prob += x[i] >= 0
prob += x[i] <= 3
prob.solve() # 問題を解く
# 結果を表示
print(LpStatus[prob.status]) # 解の状態を表示(Optimalなら最適解が求められている)
print("Optimal Value =", value(prob.objective)) # 最適値を表示
for x in prob.variables():
print(x,"=", value(x)) # 最適解を表示
制約条件を変えた場合の最適解

元の問題の最適解
お菓子6, 12, 13が3回選ばれて、お菓子5,11が1回選ばれていますね。だいたい元の問題の最適解として選ばれたお菓子と同じものが選ばれていますね。逆に選ばれなかったお菓子9について考察するのも面白そうです。
2個目以降は満足度が下がるように設定する
次に2個目以降の満足度が減少するように設定します。現実的に考えたら1個目のお菓子より2個目のお菓子の方が満足度が低くなるはずです。
こういうのを経済学の用語で限界効用逓減の法則と言います!
このことを制約条件に反映させてみましょう。今回は割引率\(\delta\)(\(0<\delta<1\))を用いてモデル化しました。簡単に説明すると2個目以降は満足度が\(\delta\)だけ割り引かれるように目的関数を設定します。
この部分の説明はちょっと長いので、数式とコードの説明は次の記事に書くことにして、この記事ではコードと結果だけ紹介したいと思います。
説明はこの記事で解説しています!
現在制作中
それではコードは以下のようになります。割引率は0.5、最大3個まで購入可能の条件で設定しました。
## ナップザック問題を解くための前準備
# pulpをインポート
! pip install pulp
from pulp import *
# pandasをインポート
import pandas as pd
# numpyをインポート
import numpy as np
# 満足度vをランダムに設定
np.random.seed(100)
v = np.random.randint(10, 100, 20)
# 価格wをランダムに設定
np.random.seed(200)
w = np.random.randint(10, 300, 20)
# 予算の上限を設定
capacity = 300
## ナップザック問題を設定して実際に解いてみる
# LpMaximizeで最大化に設定
prob = LpProblem(sense=LpMaximize)
# 変数の定義(まとめて定義)ここを変更する!!!!!!!!!!!!!!!!!!!!
x = [LpVariable(f"x{i}", cat = LpBinary) for i in range(1,21)]
y = [LpVariable(f"y{i}", cat = LpBinary) for i in range(1,21)]
z = [LpVariable(f"z{i}", cat = LpBinary) for i in range(1,21)]
# 割引率の設定 ここを変更する!!!!!!!!!!!!!!!!!!!!!!!!!!!!
delta = 0.5
# 問題の設定
# 目的関数を設定 ここを変更する!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!
prob += lpDot(v, x) + (delta*lpDot(v, y)) + (delta**2*lpDot(v, z))
# 制約条件を設定 ここを変更する!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!
prob += lpDot(w, x) + lpDot(w, y) + lpDot(w, z) <= capacity
prob += x >= y >= z
prob.solve() # 問題を解く
# 結果を表示
print(LpStatus[prob.status]) # 解の状態を表示(Optimalなら最適解が求められている)
print("Optimal Value =", value(prob.objective)) # 最適値を表示
# 各お菓子の購入個数をデータフレームで表示
x_val = np.array([value(x[i]) for i in range(20)])
y_val = np.array([value(y[i]) for i in range(20)])
z_val = np.array([value(z[i]) for i in range(20)])
df = pd.DataFrame(data=x_val+y_val+z_val, index = [f"お菓子{i}" for i in range(1,21)],columns=["購入個数"])
df
割引率を設定しなかったときはお菓子6,12,13を3個買っていましたが、2個目以降は満足度が割り引かれるように設定したのでどれも最大で2個しか買っていませんね。
要はめっちゃ欲しいお菓子があっても3個以上買う気にはならないってことです。もちろんこれは割引率\(\delta\)を0.5にしているからです。1個目の満足度が80だとしたら2個目は40、3個目は20まで下がってしまいます。
割引率\(\delta\)が変われば結果も変わるので色々変更してみると面白いかもしれません。
おわりに
いかがでしたか。
今回の記事ではナップサック問題について解説していきました。
今後もこのような経営工学に関する記事を書いていきます!
最後までこの記事を読んでくれてありがとうございました。





