こんにちは!しゅんです!
今回はクラスカル法のアルゴリズムを説明していきたいと思います!
クラスカル法はグラフ理論で登場する数学用語で、重み付きグラフの最小全域木を見つけるための手法の一つです。
それでは解説していきましょう!
普段は組合せ最適化の記事を書いてたりします。
ぜひ他の記事も読んでみてください!
このブログの簡単な紹介はこちらに書いてあります。
興味があったら見てみてください。
このブログでは経営工学を勉強している現役理系大学生が、経営工学に関することを色々話していきます!
ぼくが経営工学を勉強している中で感じたことや、興味深かったことを皆さんと共有出来たら良いなと思っています。
そもそも経営工学とは何なのでしょうか。Wikipediaによると
経営工学(けいえいこうがく、英: engineering management)は、人・材料・装置・情報・エネルギーを総合したシステムの設計・改善・確立に関する活動である。そのシステムから得られる結果を明示し、予測し、評価するために、工学的な分析・設計の原理・方法とともに、数学、物理および社会科学の専門知識と経験を利用する。
引用元 : 経営工学 – Wikipedia
長々と書いてありますが、要は経営、経済の課題を理系的な観点から解決する学問です。
具体例を使ってクラスカル法のアルゴリズムを説明する
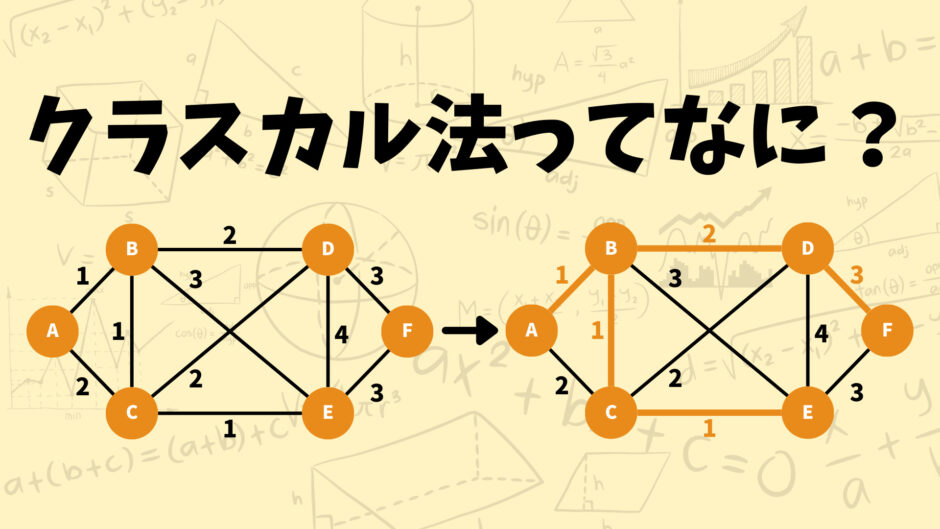
まず最初に下のグラフを使ってクラスカル法のアルゴリズムを説明していきます。
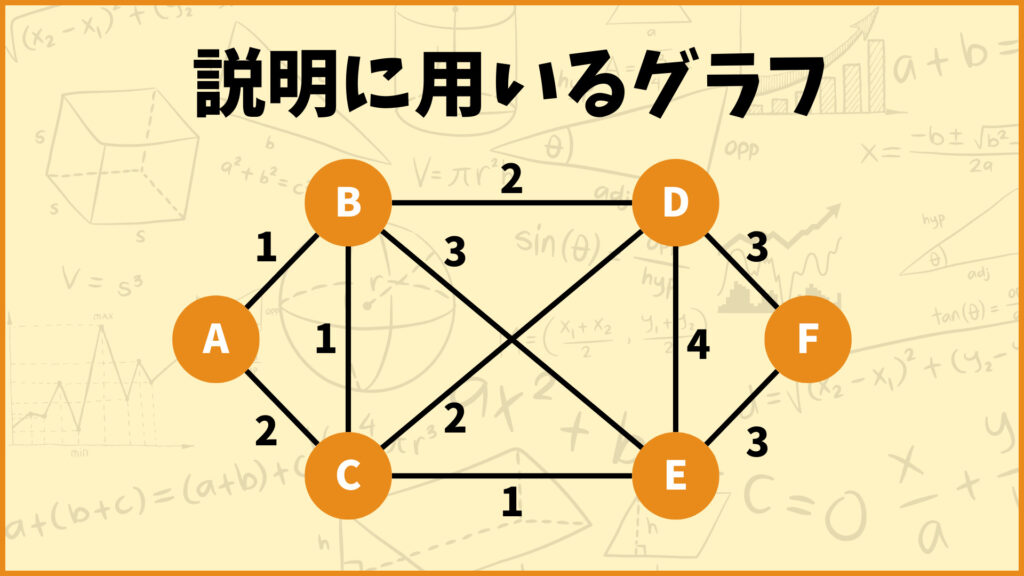
このグラフの最小全域木は下の図のようになります。
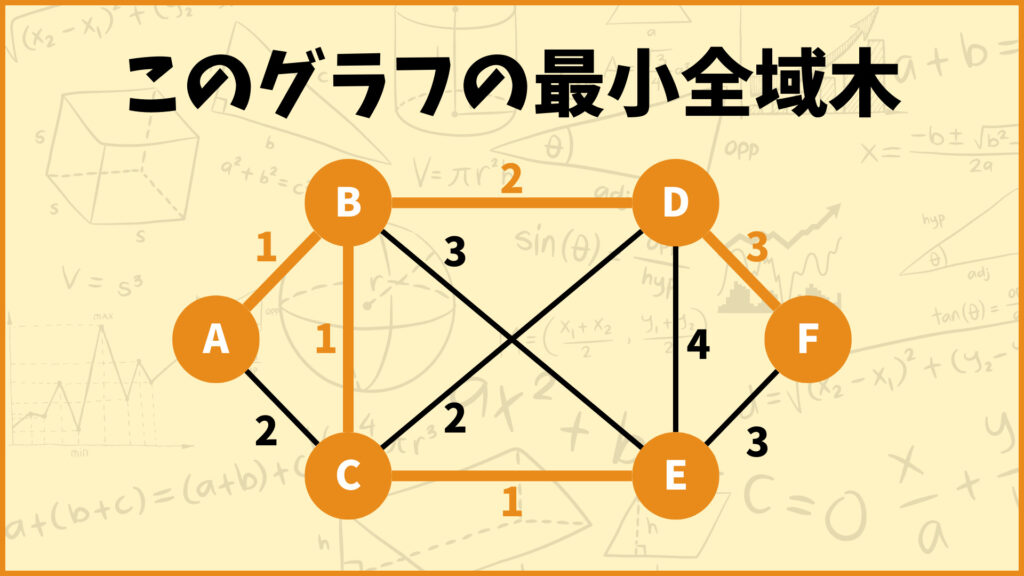
それではこのグラフの最小全域木を求める手順を1つずつ解説していきます!
STEP.1 重みが小さい辺から考える
クラスカル法では重みが小さい辺から順番に考えていきます。今回のグラフだと下のようにまとめることができます。
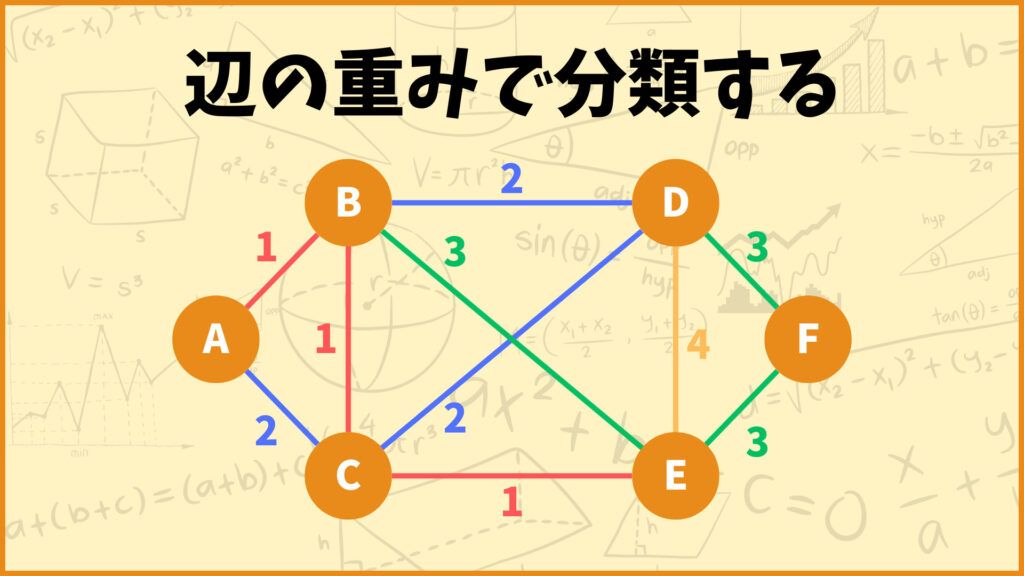
辺の重みで分類する
辺の重みが1:(A,B), (B,C), (C,E)
辺の重みが2:(A,C), (B,D), (C,D)
辺の重みが3:(B,E), (D,F), (E,F)
辺の重みが4:(D,E)
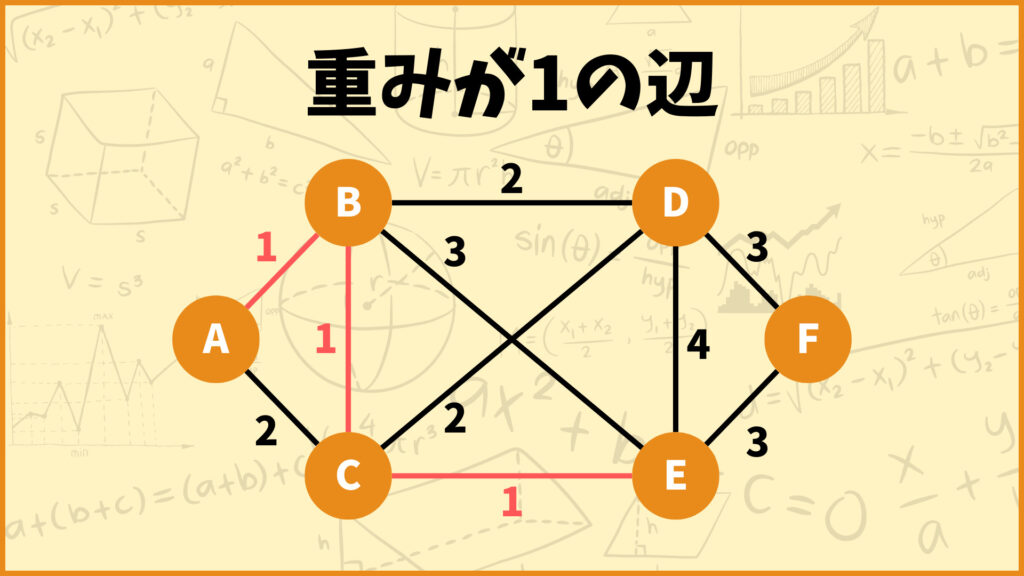
STEP.2 重みが1の辺を選ぶ
まず重みが1の辺から考えます。
最小全域木の辺として採用するかどうかは、その辺を採用したときに、採用した辺だけを使って閉路ができるかどうかで決めます。
閉路ができない:その辺を採用する
閉路ができる:その辺を採用しない
今回はすべての辺を採用しても閉路ができないので、重みが1の辺を全て採用します。
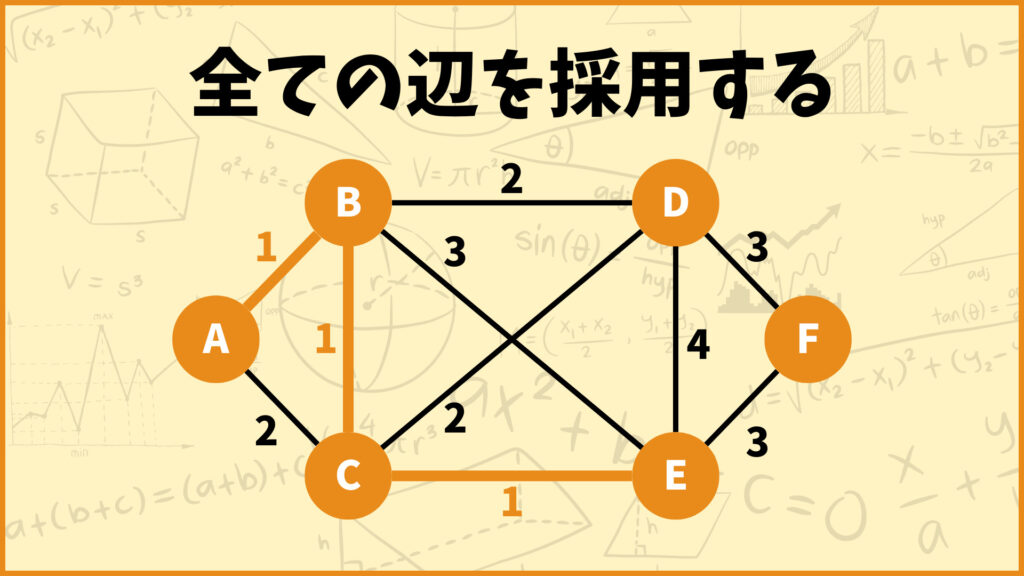
例えば下のグラフの場合をについて考えてみましょう。このグラフ見ると重みが1の辺が4つあります。
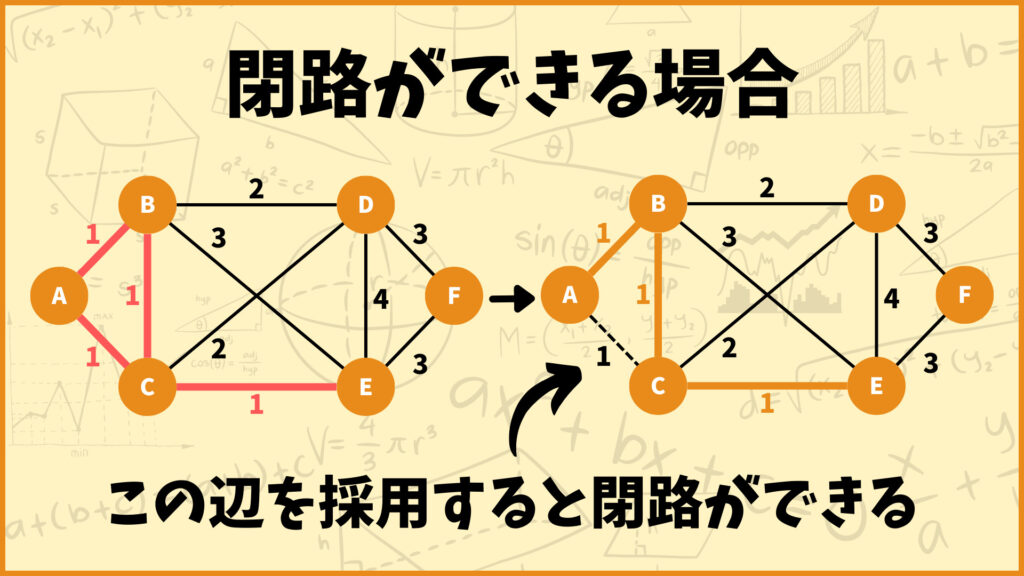
ところがこれらの辺を全て採用してしまうとA-B-C-Aの閉路ができてしまいます。閉路ができると木ではなくなってしまうので、辺(A,B)、辺(A,C)、辺(B,C)を全て最小全域木中の辺として採用することはできないです。
上図の右側の例は辺(A,C)を最小全域木の辺として採用しなかった場合について表しています。これを見ると、ちゃんと閉路が存在していない状態になっていますね。
STEP.3 重みが2の辺を選ぶ
次に重みが2の辺を選びます。
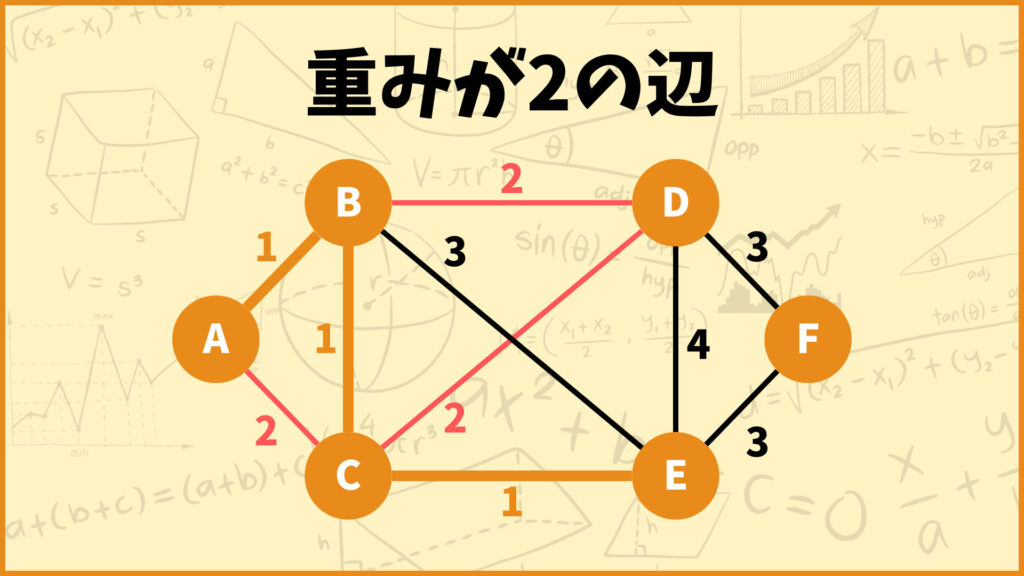
これらの辺を追加したときに閉路ができなければその辺を採用し、閉路ができればその辺を採用しません。
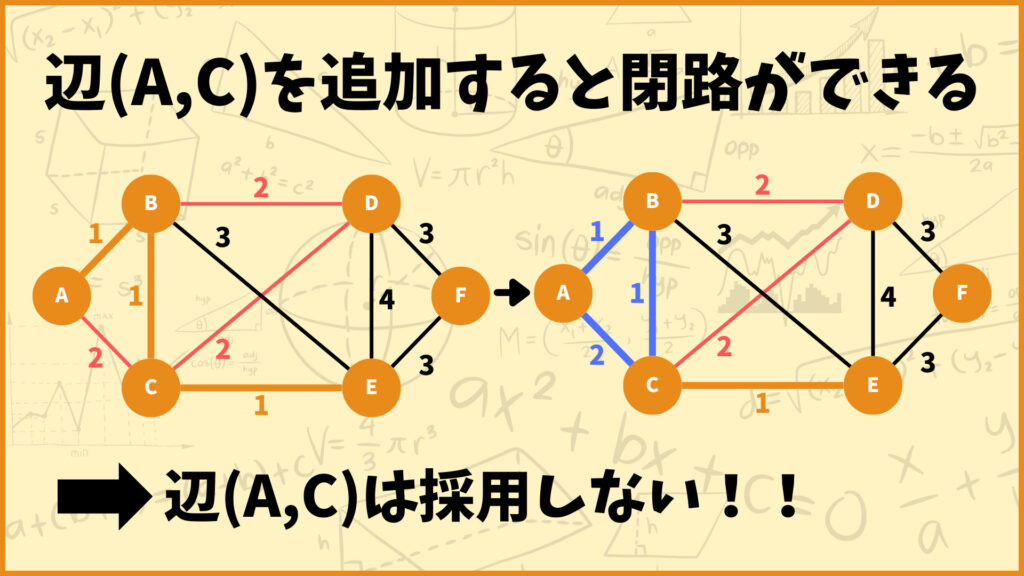
辺(A,C)を追加しようとするとA-B-C-Aの閉路ができてしまうので、辺(A,C)は採用しません。
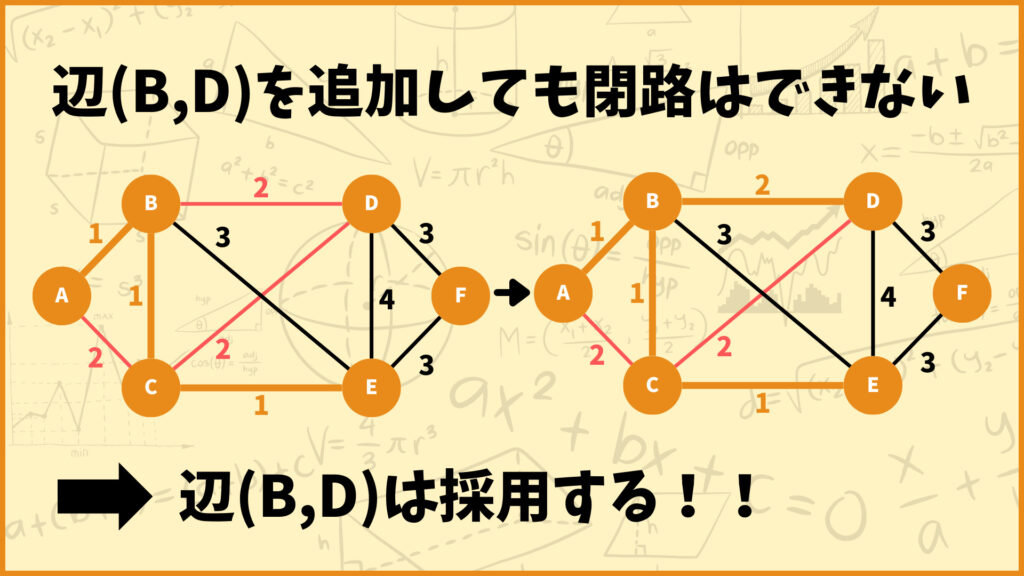
辺(B,D)を追加しようとしても閉路はできません。そのため辺(B,D)は採用します。
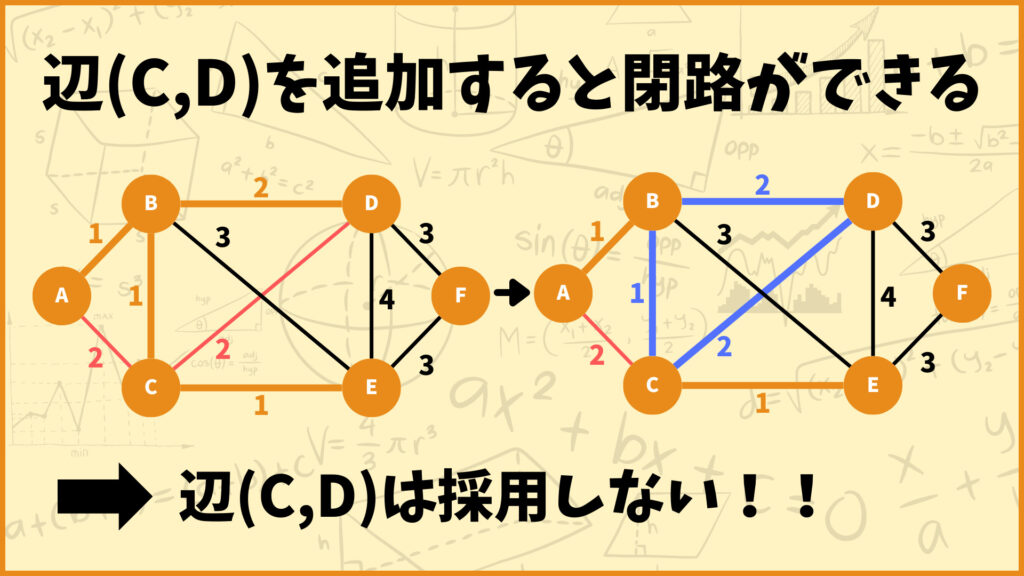
辺(C,D)を追加しようとするとC-B-D-Cの閉路ができてしまうので、辺(C,D)は採用しません。
従って重みが2までの辺を採用するかどうか考えた結果、下の図のような状態になります。
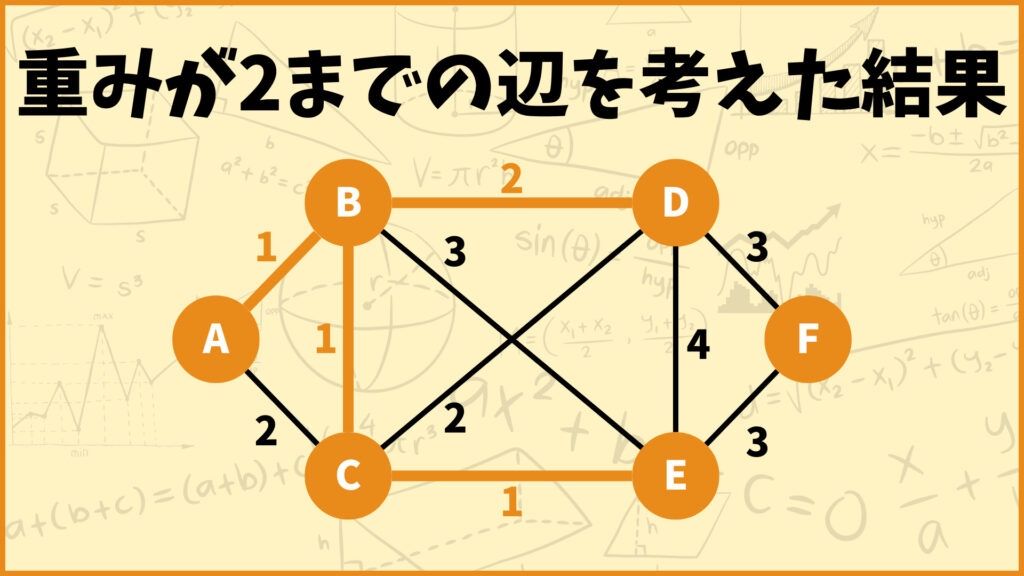
STEP.4 重みが3の辺を選ぶ
次に重みが3の辺を選びます。
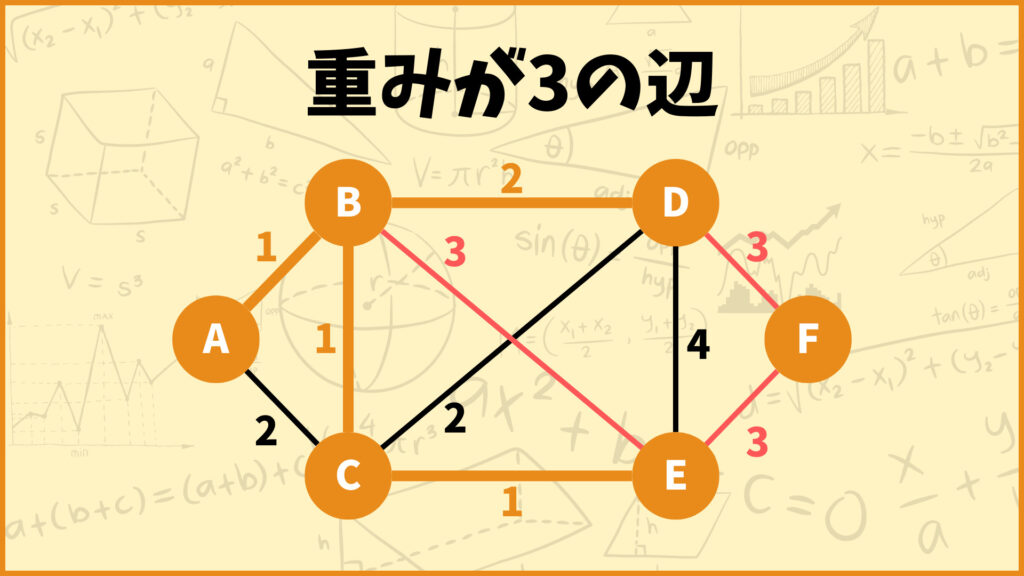
先ほどと同じように、その辺を追加したときに閉路ができるかどうかでその辺を採用するかどうかを判断します。やることは一緒なので1つの図にまとめて説明したいと思います。
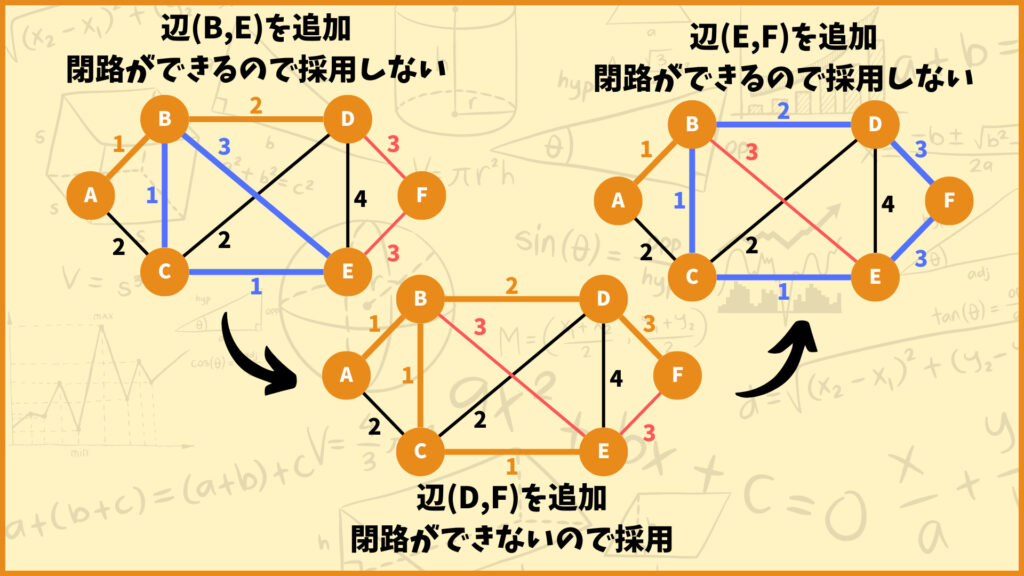
まず辺(B,E)を追加しようとするとB-C-E-Bの閉路ができてしまうので、辺(B,E)は採用しません。
次に辺(D,F)を追加しようとしても閉路ができないので、辺(D,F)を採用します。
最後に辺(E,F)を追加しようとするとB-D-F-E-C-Bの閉路ができてしまうので、辺(E,F)は採用しません。
以上より、重みが3までの辺を採用するかどうか考えた結果が下のグラフのようになります。
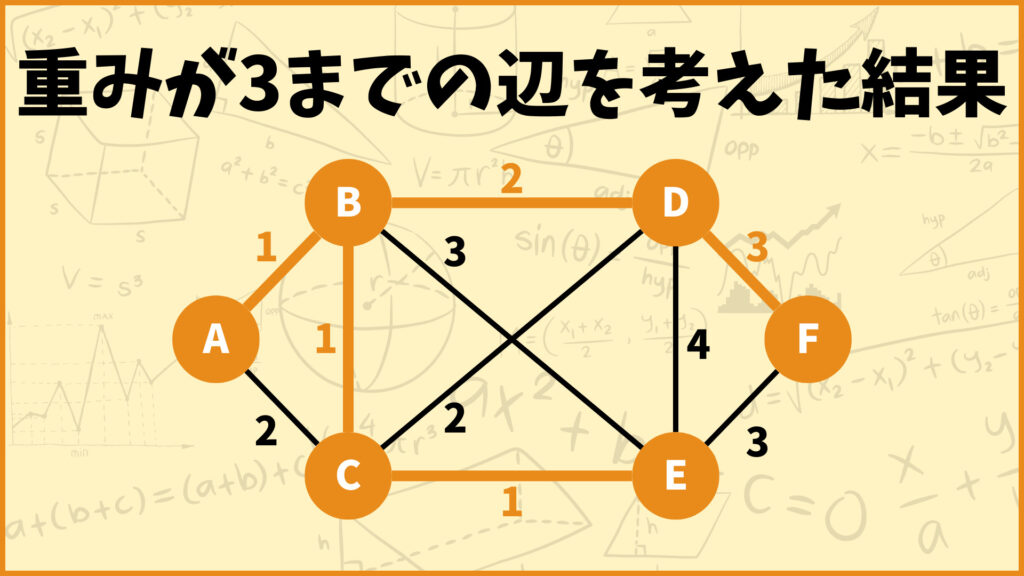
実はこの時点で最小全域木が完成していますが、一応辺の重みが4の場合も確認してみましょう。
STEP.5 重みが4の辺を選ぶ
最後に重みが4の辺を選びます。
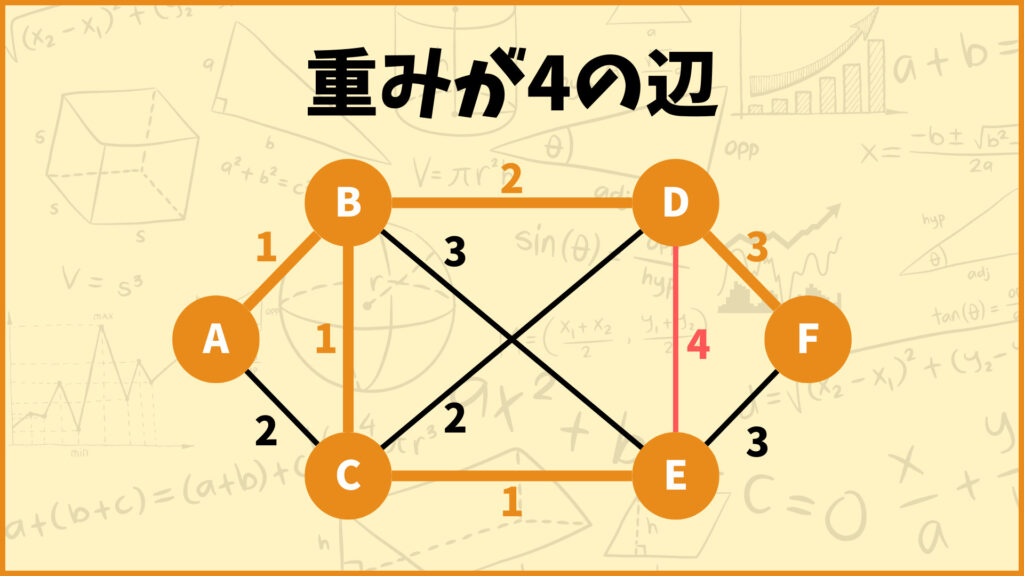
しかしこの辺(D,E)を追加するとB-D-E-C-Bの閉路ができてしまうので辺(D,E)は採用しません。
以上より、最終的に得られるグラフが最小全域木となります。

クラスカル法のアルゴリズム
ここまでは具体例を使ってクラスカル法のアルゴリズムを説明しましたが、最後により一般的なアルゴリズムの説明をしたいと思います。
上の具体例の説明と照らし合わせながら見ると理解しやすいと思います。
↓↓↓クラスカル法のアルゴリズム↓↓↓
- 重みが小さい順に辺\(e_1,\; e_2,\; …, \; e_m\)を並べる。
(\(c(e_1) \leq c(e_2) \leq …\leq c(e_m)\):\(c(e_i)\)は辺\(e_i\)の重み) - \(T=\emptyset\)とする。
- \(i=1,2,…,m\)に対して
もし\(T \cup e_i\)が閉路を持たないなら\(T\)に辺\(e_i\)を追加する。 - \(T\)を出力する。
イメージ的には最小全域木中の辺として採用する辺を\(T\)に追加していくという感じです。
おわりに
いかがでしたか。
今回の記事ではクラスカル法について解説していきました。
今後もこのような経営工学に関する記事を書いていきます!
最後までこの記事を読んでくれてありがとうございました。
参考文献
Ding-Zhu Du, Panos M. Pardalos, Xiaodong Hu, Weili Wu, Introduction to Combinatorial Optimization. Springer, 2022, p.4