～正規分布ってなに？～統計検定2級を勉強してみよう！【経営工学を専門にしている大学生の日記】

はじめに

こんにちは！しゅんです！

今回は正規分布について解説していきます！

正規分布は確率・統計でおそらく最もよく登場する数学用語です。この記事では正規分布について図を使って分かりやすく解説していきます。

また今回はpythonを使って正規分布を扱っていこうと思います。

それでは解説していきましょう！

統計検定2級に関する他の記事はこちらから見れます！
ぜひ他の記事も読んでみてください！

もっとみる

このブログの簡単な紹介はこちらに書いてあります。
興味があったら見てみてください。

このブログについて

このブログでは経営工学を勉強している現役理系大学生が、経営工学に関することを色々話していきます！

ぼくが経営工学を勉強している中で感じたことや、興味深かったことを皆さんと共有出来たら良いなと思っています。

そもそも経営工学とは何なのでしょうか。Wikipediaによると

経営工学（けいえいこうがく、英: engineering management）は、人・材料・装置・情報・エネルギーを総合したシステムの設計・改善・確立に関する活動である。そのシステムから得られる結果を明示し、予測し、評価するために、工学的な分析・設計の原理・方法とともに、数学、物理および社会科学の専門知識と経験を利用する。

引用元 : 経営工学 – Wikipedia

長々と書いてありますが、要は経営、経済の課題を理系的な観点から解決する学問です。

正規分布ってなに？

正規分布は統計学でおそらく最もメジャーな確率分布で、自然界の社会における多くの現象を近似するためによく使われます。

正規分布のグラフは下のようになります。

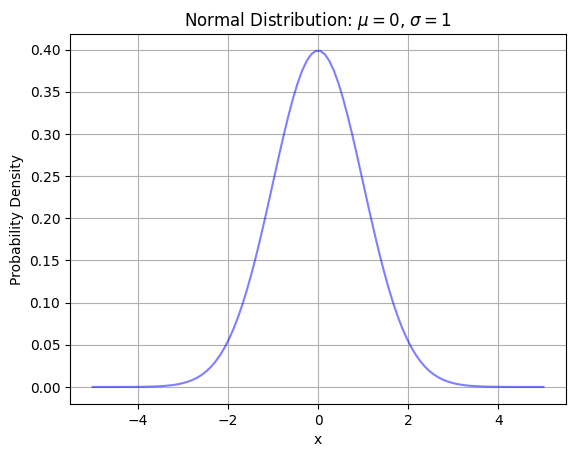
正規分布は連続型確率分布なのでこのグラフは確率密度関数を表しています。

連続型確率分布と確率密度関数はこちらの記事で詳しく解説しています！

2023年5月19日～離散型確率分布と連続型確率分布ってなに？～統計検定2級を勉強してみよう！【経営工学を専門にしている大学生の日記】

さきほど世の中の様々な現象を正規分布で近似すると言ったので、これの説明をしようと思います。例えば1000人の学生のテストの点数をヒストグラムで表してみると以下のようになりました。

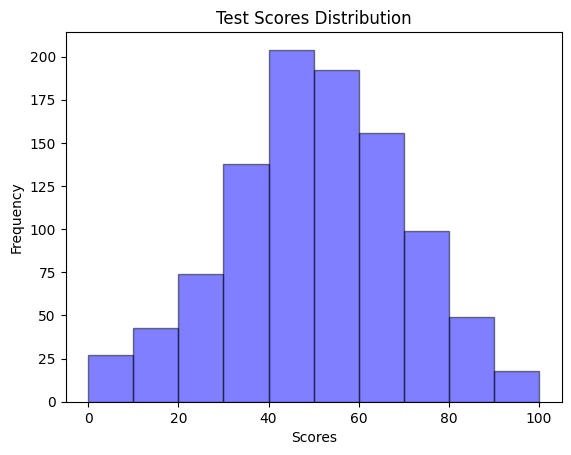
このヒストグラムを見ると真ん中の40点～60点くらいの人が一番多くて、端にいくにつれてどんどん人が少なくなっていますね。これって正規分布のグラフと似ていませんか？

実は世の中こういう分布になる現象って以外と多いんですよね。そしてこういう分布になるときに、この現象は正規分布に近似できるという風になるんです。

（※上のデータは正規分布に従うようにぼくが作った架空のデータなので実際のデータではありません笑）

でも実際に正規分布に近似できそうなデータは結構あるんです。例えば前ぼくが分析した、「NBA選手の2P%の分布」は結構正規分布に従っていそうでした。

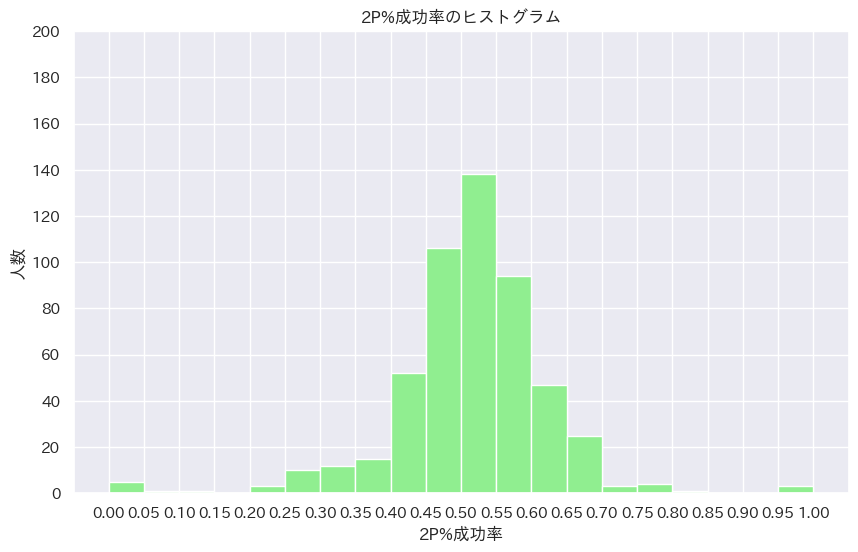
なんか正規分布っぽいですよね。

実際には正規分布に従うかどうかを判定する方法がいくつかあるのでそれを使って判断します。

後でも説明しますが、データの分布が正規分布に近似できると色々便利なんですよね。だから正規分布って色んな所で使われるんです。

最後に正規分布の確率密度関数の式を見せます。

\(f(x) = \frac{1}{\sqrt{2\pi\sigma^2}} \, e^{-\frac{(x-\mu)^2}{2\sigma^2}}\)

まじで訳わかんない関数に見えますが大丈夫です。統計検定2級ではこの式を覚える必要ないのでこんなに難しい式なんだ程度でOKです。

正規分布の期待値と分散

これまで解説してきた、例えば二項分布は試行回数\(n\)と成功確率\(p\)を自分で決めれば期待値と分散が計算できましたが、正規分布は期待値と分散自体を自分で決めます。

例えばこの分布は期待値50、分散が100の正規分布に従うみたいな感じで表します。より数学的に表すと、期待値\(\mu\)、分散\(\sigma^2\)に従う正規分布は\(N(\mu,\sigma^2)\)と表記します。

確率変数Xが期待値50、分散100の正規分布に従うとき

\(X\) ～ \(N(50,100)\)

期待値はその確率分布が取る値の平均を表します。例えばテストの点数が期待値50の正規分布に従うとき、理論的にはそのテストの平均点が50点になるということを表しています。。分散はその確率分布が取る値にどれだけばらつきがあるかを表します。

標準正規分布ってなに？

正規分布の中に標準正規分布というものがあります。これは非常に重要な分布でどんな正規分布でも標準化という変換をすることによって得られます。

ということでこの章では標準正規分布がどのような分布なのか、そして標準化がどんな変換かについて解説したいと思います。それではいってみましょう。

標準正規分布は期待値0、分散1の正規分布

結論標準正規分布は期待値0、分散1の正規分布のことです。グラフにすると下のような式になります。

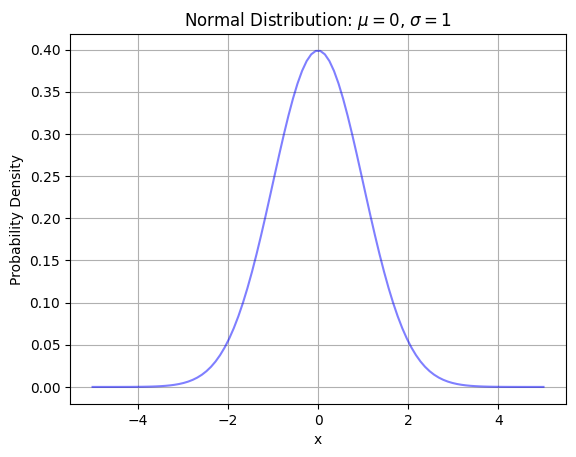
標準正規分布の確率密度関数の式は下のようになります。（統計検定2級ではこの式を覚える必要はないです。）

\(f(x) = \frac{1}{\sqrt{2\pi}} \, e^{-\frac{x^2}{2}}\)

先ほど説明した式に\(\mu=0\)、\(\sigma^2=1\)を代入したら計算できます。

この標準正規分布は統計学でよく行う推定や仮説検定において非常に便利な分布なんです。そのためできれば標準正規分布に従っているって考えたいんですよね。

でも考えてみたら標準正規分布って期待値0、分散1の正規分布っていう非常に限られた範囲でしか扱えないんですよね。そこで登場するのが標準化です。標準化を使えばどんな正規分布でも標準正規分布に変換することができます。

ということで次に標準化について解説したいと思います。

標準化ってなに？

結論標準化は、正規分布に従う確率変数から期待値を引いて標準偏差で割ることです。

標準化の計算式

\(X\)を確率変数とする。

標準化の計算式：\(\frac{X-\mu}{\sigma}\)

例えば\(X\)～\(N(50,100)\)（確率変数\(X\)が期待値50、分散100の正規分布に従う）のとき\(Z=\frac{X-50}{10}\)とすると\(Z\)～\(N(0,1)\)（確率変数\(Z\)は標準正規分布に従う）となります。

このようにしてどんな正規分布でも標準正規分布に変換することができます。

標準化はこちらの記事で詳しく解説しています！

2023年1月9日データの標準化～pythonでデータ分析をしてみよう～【経営工学を専門にしている大学生の日記】

正規分布をpythonで扱う

最後にpythonを使って正規分布を扱いたいと思います。プログラミングの知識が必要なので、分からなければプログラムの所は飛ばして結果だけ確認してみてください。

事前準備

pythonで確率・統計を扱うときはscipyというライブラリをよく使います。その中でも今回は正規分布を扱いたいのでnormをインポートします。normは正規分布(normal distribution)のことです。また数値計算でよく使うnumpy、グラフ作成でよく使うmatplotlibというライブラリもインポートしておきます。

import numpy as np
import matplotlib.pyplot as plt
import scipy.stats as stats
from scipy.stats import norm

正規分布の確率を計算する

ということでまずは期待値50、標準偏差10として正規分布の確率密度関数を計算します。例えば確率変数\(X\)が40から60の間にある確率を求めてみましょう。

# 期待値と標準偏差の設定
mu = 50
sigma = 10

# 正規分布の確率密度関数を定義
normal_dist = norm(mu, sigma)

# 40から60の範囲の確率を求める
lower = 40
upper = 60
probability = normal_dist.cdf(upper) - normal_dist.cdf(lower)

print("40から60の間にある確率:", probability)

ということで期待値50、標準偏差10の正規分布において40から60の間にある確率は約0.68であることが分かりました。

テストの点数で置き換えてみると、平均点50、標準偏差10のテストにおいて点数が40点～60点の間に約68%の人が分布しているということを表しています。

正規分布の確率密度関数をグラフ化する

次にこの正規分布をグラフ化してみましょう。つまり期待値50、標準偏差10の正規分布の確率密度関数をグラフで表示します。

# 平均と標準偏差の定義
mu = 50  # 平均
sigma = 10  # 標準偏差

# 範囲とステップサイズの定義
x = np.linspace(0, 100, 100)  # x軸の範囲とステップサイズ

# 正規分布の確率密度関数の計算
y = norm.pdf(x, mu, sigma)  # 確率密度関数の値を計算

# プロット
plt.plot(x, y, color = "blue", alpha = 0.5)
plt.xlabel("x")
plt.ylabel("Probability Density")
plt.title("Normal Distribution: $\mu=50$, $\sigma=10$")
plt.grid(True)
plt.show()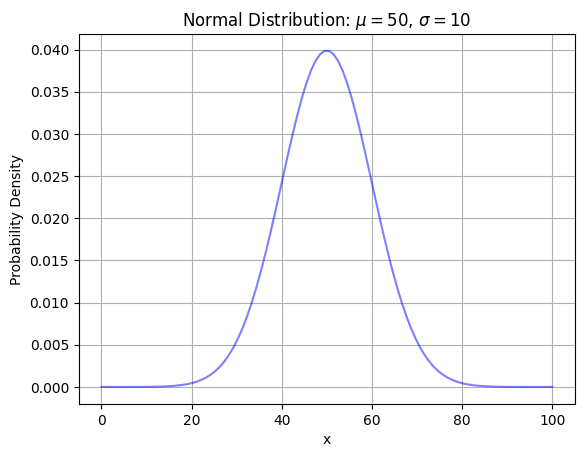

グラフを見ると分かるように、正規分布は期待値を軸として対称な形をしています。

先ほど求めた確率はこのグラフとx軸で囲まれた範囲の中で40から60の間の面積を求めています。下の図のような感じですね。

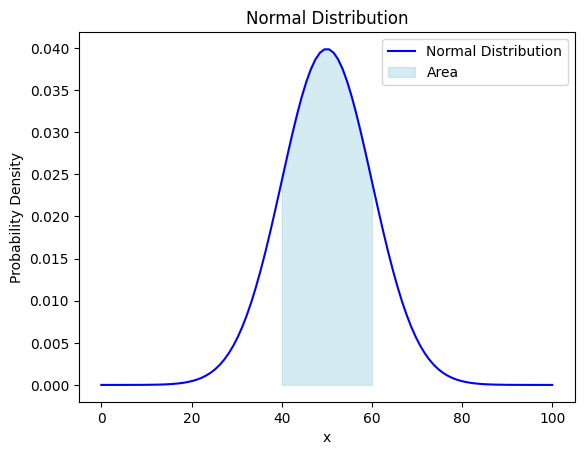
水色で塗られた部分の面積を計算した結果約0.68になったというわけです。

標準正規分布をグラフ化する

今さっき正規分布のグラフをpythonで描きましたが、あれの期待値と標準偏差をそれぞれ0と1に設定すれば標準正規分布が描けます。

# 平均と標準偏差の定義
mu = 0  # 平均
sigma = 1  # 標準偏差

# 範囲とステップサイズの定義
x = np.linspace(-5, 5, 100)  # x軸の範囲とステップサイズ

# 正規分布の確率密度関数の計算
y = norm.pdf(x, mu, sigma)  # 確率密度関数の値を計算

# プロット
plt.plot(x, y, color = "blue", alpha = 0.5)
plt.xlabel("x")
plt.ylabel("Probability Density")
plt.title("Normal Distribution: $\mu=0$, $\sigma=1$")
plt.grid(True)
plt.show()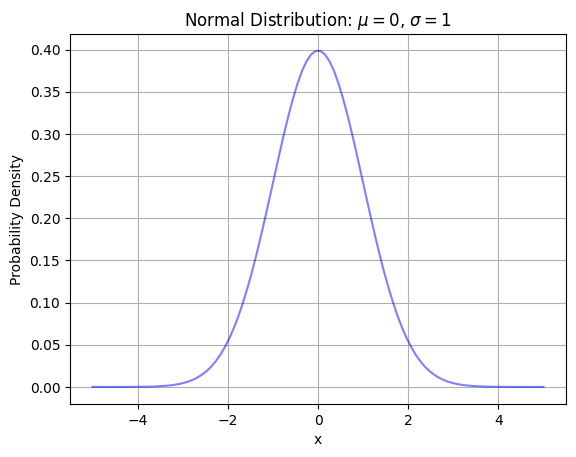

x軸のスケールもいじっているのでグラフの形的にはさっきと変わらないように見えますが、実際はこっちの方がもっとキュッとし凝縮されています。

シミュレーションしてみる

それでは実際にシミュレーションしてみましょう。先ほど期待値50、標準偏差10の正規分布において40から60の間にある確率は約0.68だと計算できました。はたして本当にそうなのかを検証します。

正規分布に従うような確率変数をランダムに10回、100回、1000回、10000回、100000回取り出したときに、取り出した値が40から60の間にある割合を計算してグラフにしてみましょう。

# 期待値と標準偏差の設定
mu = 50
sigma = 10
# 試行回数を指定
trials = [10, 100, 1000, 10000,100000]
#確率を格納する空リストを作成
result = []

for num_trials in trials:
    # 正規分布から試行を生成
    samples = np.random.normal(mu, sigma, num_trials)
    # 40から60の範囲に入る試行の数を数える
    count = np.sum((samples >= 40) & (samples <= 60))
    # 確率を計算
    probability = count / num_trials
    #確率を格納
    result.append(probability)

theo = normal_dist.cdf(60) - normal_dist.cdf(40)

# グラフを描画する
plt.plot(trials, result, marker="o", color="blue", alpha=0.5, label="Simulated")
plt.hlines(theo, 10, 100000, color="orange", label="Theoretical")
plt.xscale("log")
plt.xlabel("Number of trials")
plt.ylabel("Percentage between 40 and 60")
plt.title("Normal Distribution: $\mu=50$, $\sigma=10$")
plt.legend()
plt.show()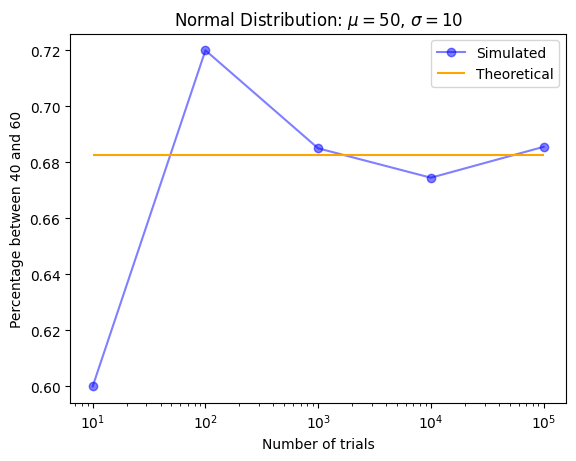

橙線が理論値を表し、青線がシミュレーションした結果の実測値を表しています。このグラフを見ると回数が少ないとき実測値は理論値からはだいぶ離れていますが、回数を増やすにつれて理論値にどんどん近づいているのが分かると思います。

ランダムに試行されるのでプログラムを実行するたびにグラフは変わりますが、基本的には試行回数が大きくなるにつれて誤差は小さくなっていくはずです。