集合\(X\)上の2項関係\(R\)のうち、以下の3つの性質を満たすものを半順序と言う。
1. 任意の\(x \in X\)に対して\((x,x) \in R\)が成立
2. 任意の\(x,y,z \in X\)に対して\((x,y) \in R,\; (y,z) \in R\)ならば\((x,z) \in R\)が成立
3. 任意の\(x,y \in X\)に対して\((x,y) \in R, \; (y,x) \in R\)ならば\(x=y\)が成立
定義を1つずつ噛み砕いていく
文字だけで書かれてもあんまりよく分からないので1つずつ説明していきます。
2項関係ってなに?
まず2項関係とは、ある集合の中から2つ要素を取ってきてペアにしたものをいくつか集めた集合です。
例えばある集合が\(X=\{1,2,3,4,5\}\)だとします。ここから適当に2つ要素を取ってきます。

上の図では(1,1), (1,4), (2,5), (3,3), (3,5), (4,5)を取ってきています。これらのペアたちをまとめて集合にしたものが2項関係です。上の例だと2項関係\(R\)は
\(R = \{(1,1), (1,4), (2,5), (3,3), (3,5), (4,5)\}\)
となります。これが2項関係です。この2項関係の中でもさっき挙げた3つの条件を満たすものが半順序という風になります。
1つ目の条件(反射律)ってなに?
次に1つ目の条件について解説したいと思います。1つ目の条件は反射律と呼ばれます。
任意の\(x \in X\)について\((x,x) \in R\)が成立
例えば\(X=\{1,2,3,4,5\}\)だったら\(R\)には(1,1), (2,2), (3,3), (4,4), (5,5)が入ってないといけないってことです。

上の図で言うと2項関係\(R_1\)には(1,1), (2,2), (3,3), (4,4), (5,5)が入っているので反射律を満たします。一方\(R_2\)には(2,2)と(4,4)がないので反射律を満たしません。
2つ目の条件(推移律)ってなに?
次に2つ目の条件について解説したいと思います。2つ目の条件は推移律と呼ばれます。
任意の\(x,y,z \in X\)について\((x,y) \in R, \; (y,z) \in R\)ならば\((x,z) \in R\)が成立

例えば2項関係\(R\)に(1,2)と(2,3)が入っているとします。このとき推移律を満たすためには\(R\)に(1,3)が入っている必要があります。
上の図で言うと\(R_1\)は推移律を満たします。一方\(R_2\)には(1,2), (2,4)が入っているのに(1,4)が入っていないので推移律を満たしません。
3つ目の条件(反対称律)ってなに?
最後に3つ目の条件について解説したいと思います。3つ目の条件は反対称律と呼ばれます。
任意の\(x,y \in X\)に対して\((x,y) \in R, \; (y,x) \in R\)ならば\(x=y\)が成立

例えば2項関係\(R\)に\((1,2)\)が入っているとします。このとき\((2,1)\)は入ってちゃダメ!って言っているのが反対称律です。
上の図で言うと\(R_1\)は反対称律を満たします。一方\(R_2\)には(1,2)と(2,1)が入っているので反対称律を満たしません。
反射律・推移律・反対称律を満たす2項関係が半順序
以上の3つの条件を満たす2項関係\(R\)のことを半順序と言います。また集合\(X\)と半順序\(R\)の組\((X,R)\)を半順序集合と言います。
ということでいくつか半順序の例を見ていきましょう。例えば集合\(X=\{1,2,3,4,5\}\)上の以下の2項関係\(R_1,R_2,R_3\)は半順序で、\(R_4,R_5,R_6\)は半順序ではありません。
半順序の例
\(R_1 = \{(1,1),(2,2),(3,3),(4,4),(5,5)\}\)
\(R_2 = \{(1,1),(2,2),(3,3),(4,4),(5,5),(1,5),(5,4),(1,4)\}\)
\(R_3 = \{(1,1),(2,2),(3,3),(4,4),(5,5),(1,2),(2,3),(2,4),(1,3),(1,4)\}\)
半順序じゃない例
\(R_4 = \{(1,1),(2,2),(3,3),(4,4)\}\)
\(R_5 = \{(1,1),(2,2),(3,3),(4,4),(5,5),(1,5),(5,4)\}\)
\(R_6 = \{(1,1),(2,2),(3,3),(4,4),(5,5),(1,2),(2,1)\}\)
半順序じゃない例を1つずつ見ていきましょう。
\(R_4\)には\((5,5)\)が入っていないので反射律を満たしません。
次に\(R_5\)を見てみましょう。\(R_5\)には\((1,5),(5,4)\)が入っていますが、\((1,4)\)が入っていないので推移律を満たしません。
最後に\(R_6\)を見てみましょう。\(R_6\)には\((1,2),(2,1)\)の両方が入っているので反対称律を満たしません。
半順序をグラフで表す
半順序集合\((X,R)\)は有向グラフとみなすことができます。集合\(X\)を頂点集合、半順序\(R\)を有向辺の集合とすることで有向グラフが書けます。
例えば以下の半順序集合\((X,R)\)をグラフにしてみましょう。
\(X=\{1,2,3,4,5\}\)
\(R=\{(1,1),(2,2),(3,3),(4,4),(5,5),\)
\((1,2),(1,3),(1,4),(1,5),(2,3),(2,4),(2,5),(3,4),(3,5)\}\)
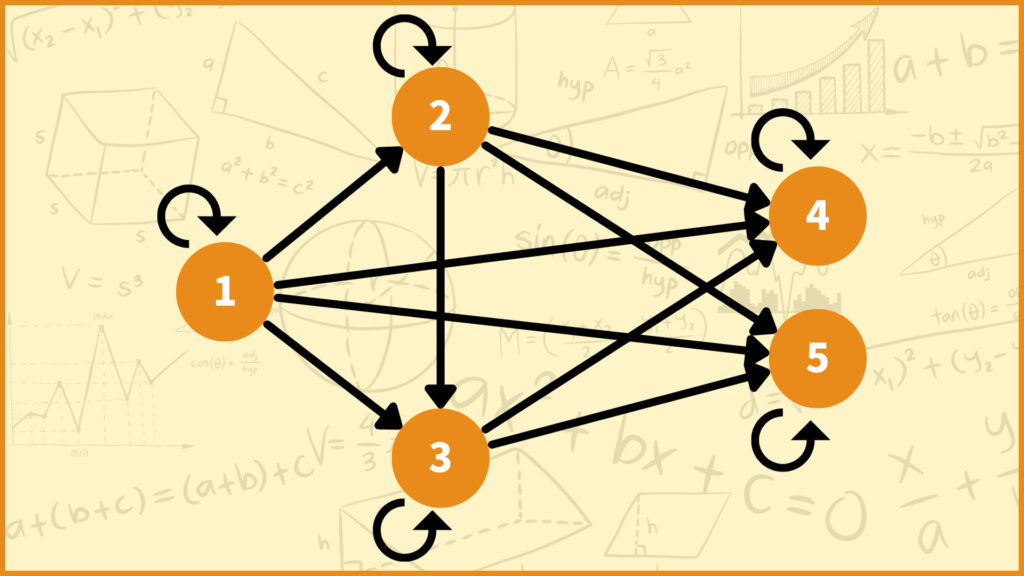
\((1,1),…,(5,5)\)は各頂点における自己ループとなります。それ以外の半順序の要素はある頂点から別の頂点への有向辺となっています。例えば\((1,3)\)は辺\((1,3)\)に対応しています。
このグラフって結構見づらいですよね。例えば半順序の定義上全ての頂点に対して自己ループが存在します。(反射律を満たすためです。)そのためこれらの自己ループは省略しても特に問題なさそうですね。
他にも色々無駄な所を省いてより簡単なグラフで表した結果、以下のようなグラフになります。
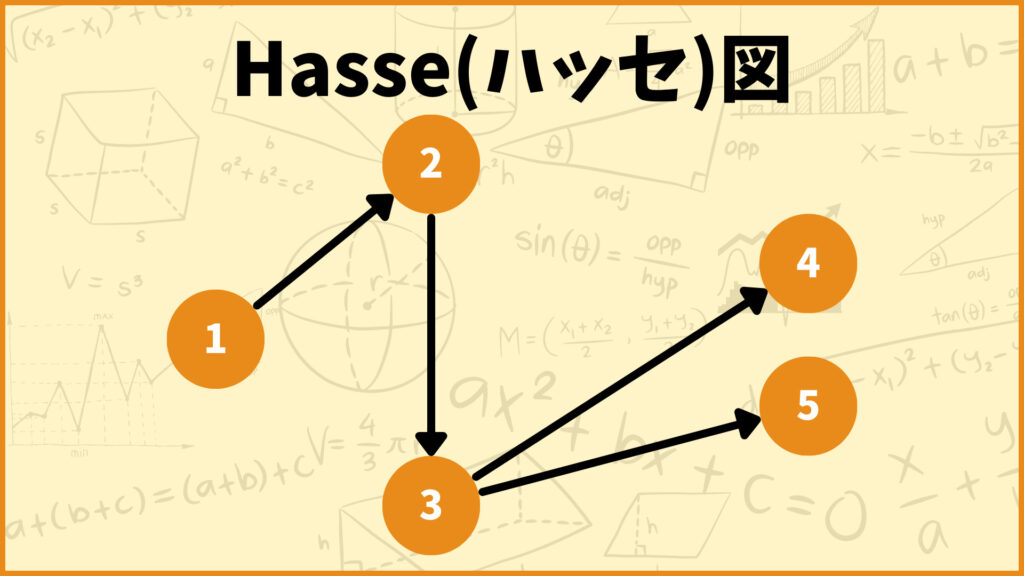
このように半順序集合を簡潔に表した有向グラフをHasse(ハッセ)図と言います。これを見ることで各頂点間がどのような関係にあるのかが一目でわかります。
Hasse(ハッセ)図はこちらの記事で解説しています!
現在制作中
おわりに
いかがでしたか。
今回の記事では半順序について解説していきました。
今後もこのような離散数学に関する記事を書いていきます!
最後までこの記事を読んでくれてありがとうございました。
普段は統計検定2級の記事を書いてたりします。
ぜひ他の記事も読んでみてください!
このブログの簡単な紹介はこちらに書いてあります。
興味があったら見てみてください。
このブログでは経営工学を勉強している現役理系大学生が、経営工学に関することを色々話していきます!
ぼくが経営工学を勉強している中で感じたことや、興味深かったことを皆さんと共有出来たら良いなと思っています。
そもそも経営工学とは何なのでしょうか。Wikipediaによると
経営工学(けいえいこうがく、英: engineering management)は、人・材料・装置・情報・エネルギーを総合したシステムの設計・改善・確立に関する活動である。そのシステムから得られる結果を明示し、予測し、評価するために、工学的な分析・設計の原理・方法とともに、数学、物理および社会科学の専門知識と経験を利用する。
引用元 : 経営工学 – Wikipedia
長々と書いてありますが、要は経営、経済の課題を理系的な観点から解決する学問です。



