- 投票ゲームってなに?
- 投票力指数ってなに?
- シャープレイ・シュービック指数をpythonで計算したい…
こんにちは!しゅんです!
今回の記事ではシャープレイ・シュービック指数をpythonで計算する方法について解説します!
それではやっていきましょう!
この記事は前回の記事の続きです。前回は投票ゲームとシャープレイ・シュービック指数がどんなものなのかを解説しています。ぜひこちらも見てみてください!
\\ 前回の記事はこちらから //
普段は組合せ最適化の記事を書いてたりします。
ぜひ他の記事も読んでみてください!
このブログの簡単な紹介はこちらに書いてあります。
興味があったら見てみてください。
このブログでは経営工学を勉強している現役理系大学生が、経営工学に関することを色々話していきます!
ぼくが経営工学を勉強している中で感じたことや、興味深かったことを皆さんと共有出来たら良いなと思っています。
そもそも経営工学とは何なのでしょうか。Wikipediaによると
経営工学(けいえいこうがく、英: engineering management)は、人・材料・装置・情報・エネルギーを総合したシステムの設計・改善・確立に関する活動である。そのシステムから得られる結果を明示し、予測し、評価するために、工学的な分析・設計の原理・方法とともに、数学、物理および社会科学の専門知識と経験を利用する。
引用元 : 経営工学 – Wikipedia
長々と書いてありますが、要は経営、経済の課題を理系的な観点から解決する学問です。
シャープレイ・シュービック指数ってなに?
まず最初にシャープレイ・シュービック指数について解説したいと思います。詳しい話は前回の記事で解説しているのでそちらもぜひ見てみてください!
\\ 前回の記事はこちらから //
ある順番で政党が提携に参加するシチュエーションを考える
まず最初に以下のシチュエーションを考えます。
政党A → 政党B → 政党Cの順番で提携に参加する

1. 政党Aだけの提携
政党Aだけの提携の場合、この提携の投票数は150票です。従ってこの時点では過半数を超えていません。
2. 政党Aと政党Bの提携
つづいて政党Aだけの提携に政党Bが加わった場合を考えます。この提携の投票数の合計は270票です。従ってこの時点で過半数を超えました。
3. 政党Aと政党Bと政党Cの提携
政党Aと政党Bの提携の時点で過半数を超えているので、この提携に政党Cが加わっても投票数の合計は過半数を超えています。
ピボットプレイヤーを考える
政党Bに着目してみましょう。自身が提携に参加するまでは過半数を超えていませんでしたが、自分が提携に参加したら過半数を超えました。このようなプレイヤーのことをピボットプレイヤー(pivot player)と言います。
イメージとしてはピボットプレイヤーは自分の力によって過半数の成立を左右できる存在のことです。
上の例では政党A→政党B→政党Cの順番で提携に参加するシチュエーションを考えたのでピボットプレイヤーは政党Bでしたが、順番が変わればピボットプレイヤーも変わります。

例えば政党B→政党C→政党Aの順番で提携に参加する場合を考えます。このときは政党Aが提携に参加して初めて過半数を超えるので、ピボットプレイヤーは政党Aとなります。
全ての順列に対してピボットプレイヤーを考える
シャープレイ・シュービック指数を計算するためには全ての順列に対してピボットプレイヤーを考える必要があります。今回の例だとプレイヤーの数は3つなので、\(3!=6\)通りの順列を考える必要があります。
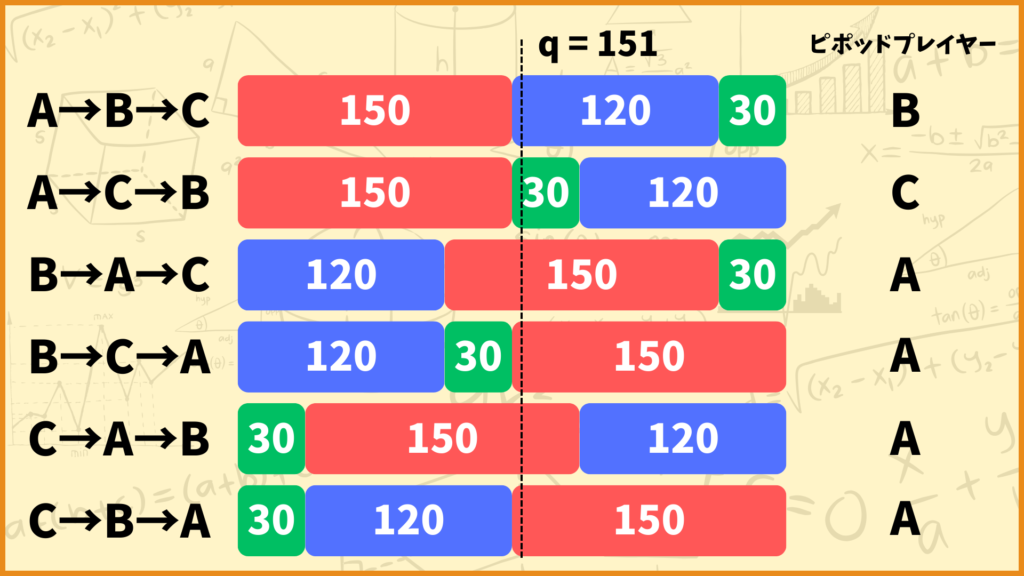
ということで全ての順列に対してピボットプレイヤーを考えることができました。ここまで出来たらシャープレイ・シュービック指数を計算することができます。シャープレイ・シュービック指数の計算式は下記の通りです。
\(\text{プレイヤー}i\text{のS-S指数} = \frac{\text{プレイヤー}i\text{がピボットプレイヤーになった回数}}{\text{順列の総数}}\)
(S-S指数はシャープレイ・シュービック指数の略)
3人のプレイヤーの場合、分母は6になりますね。この式に従って各政党のシャープレイ・シュービック指数を計算してみましょう。
政党A:\(\frac{4}{6}=0.6666…\)
政党B:\(\frac{1}{6}=0.1666…\)
政党C:\(\frac{1}{6}=0.1666…\)
ということで各政党のシャープレイ・シュービック指数を計算することができました。これを見ると政党Cは政党Bと同じくらいの影響力を持っていて、政党Aは政党Bの4倍の影響力を持っていることが分かります。
実はシャープレイ・シュービック指数は投票ゲームにおけるシャープレイ値なんです。シャープレイ値は提携型ゲームにおける配分の1つで、各プレイヤーの限界貢献度をもとに計算されます。投票ゲームにおいては各プレイヤーがピボットプレイヤーのときに限界貢献度が1、それ以外の場合は限界貢献度は0となります。(機会があったら今度シャープレイ値の記事も書こうと思います。)
pythonでシャープレイ・シュービック指数を計算するコード
コードの全貌
# 順列を生成するために使用するモジュール
from itertools import permutations
def compute_shapley_shubik_index(seats, threshold):
# 全ての順列を生成する
all_permutations = list(permutations(seats))
# シャープレイ・シュービック指数の初期値を生成
SS_index = {party: 0 for party in seats}
# すべての順列についてピボットプレイヤーを探す
for perm in all_permutations:
total_seats = 0
for party in perm:
total_seats += seats[party]
if total_seats >= threshold:
SS_index[party] += 1
break
# 順列の総数で割り算する
total_permutations = len(all_permutations)
SS_index = {party: count / total_permutations for party, count in SS_index.items()}
return SS_index
上のコードを実行すればシャープレイ・シュービック指数が計算できます。詳しく解説していきます。
コードの解説
# 順列を生成するために使用するモジュール
from itertools import permutationsまず最初に、事前準備として「itertools」から「permutations」をインポートします。「permutation」は順列を生成するために使用します。
def compute_shapley_shubik_index(seats, threshold):ここでは関数を定義しています。「compute_shapley_shubik_index」という関数名にしました。引数は「seats」と「threshold」で、「seats」は各政党の議席数、「threshold」は閾値を表しています。
# 全ての順列を生成する
all_permutations = list(permutations(seats))ここでは全ての順列を生成してリストにしています。ここで先ほどインポートした「permutations」を使用しています。
# シャープレイ・シュービック指数の初期値を生成
SS_index = {party: 0 for party in seats}ここではシャープレイ・シュービック指数の初期値を生成しています。初期値なので全ての政党に対して値は0に設定しています。
# すべての順列についてピボットプレイヤーを探す
for perm in all_permutations:
total_seats = 0
for party in perm:
total_seats += seats[party]
if total_seats >= threshold:
SS_index[party] += 1
break
ここでは全ての順列に対してピボットプレイヤーを探しています。「threshold」を超すまで政党の議席数を「total_seats」に足していき、「threshold」を超えたところでfor文をbreakして次の順列の処理に進みます。
またピボットプレイヤーの「SS_index」にはプラス1しています。
# 順列の総数で割り算する
total_permutations = len(all_permutations)
SS_index = {party: count / total_permutations for party, count in SS_index.items()}1個前の計算で求めた「SS_index」の値を順列の総数で割り算します。
return SS_index最終的に計算されたシャープレイ・シュービック指数を返します。
具体例を使って実際に計算してみる
それでは最後に具体例を使って実際にシャープレイ・シュービック指数を計算してみたいと思います。
具体例1
政党数:3
各政党の議席数(計300議席)
政党A : 150
政党B:120
政党C:30
閾値:151(過半数)
上の問題例に対してシャープレイ・シュービック指数を計算してみましょう。
# プレイヤーの議席数
seats = {
"A" : 150,
"B" : 120,
"C" : 30
}
# 閾値
threshold = 151
SS_index = compute_shapley_shubik_index(seats, threshold)
for party in seats:
print(f"政党{party}のS-S指数:{SS_index[party]}")
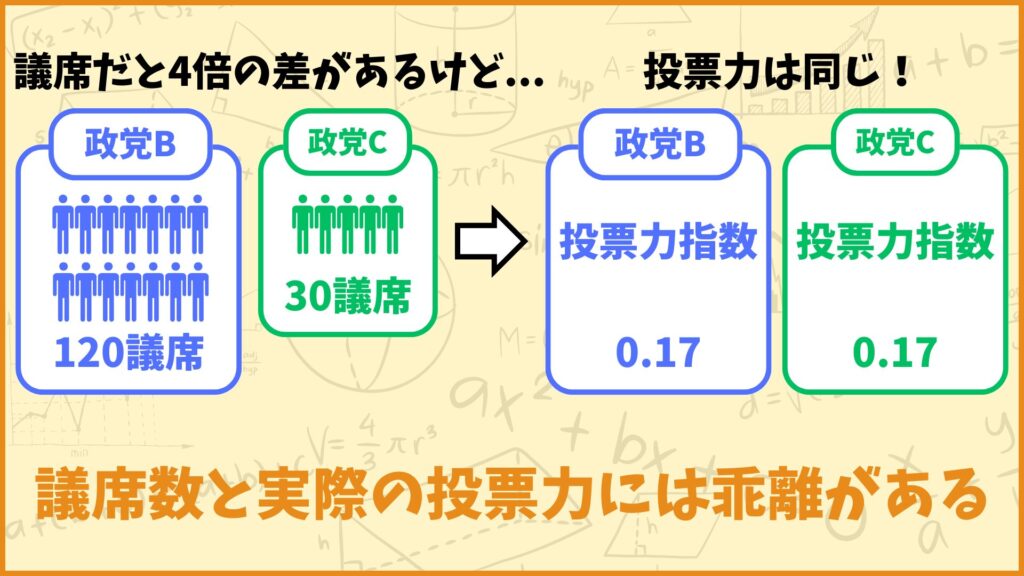
議席数で言えば政党Bは政党Cの4倍ですが、シャープレイ・シュービック指数で言うと政党Bも政党Cも同じ程度の影響力となっています。
具体例2
政党数:5
各政党の議席数(計450議席)
政党A : 250
政党B:100
政党C:50
政党D:30
政党E:20
閾値:226(過半数)
具体例2は1つの政党だけで閾値(過半数)を超えている問題例です。
# プレイヤーの議席数
seats = {
"A" : 250,
"B" : 100,
"C" : 50,
"D" : 30,
"E" : 20
}
# 閾値
threshold = 226
SS_index = compute_shapley_shubik_index(seats, threshold)
for party in seats:
print(f"政党{party}のS-S指数:{SS_index[party]}")
この場合のシャープレイ・シュービック指数は、政党Aが1でそれ以外の政党は0になってしまいました。政党Aが提携に参加しなければどんな提携も勝利提携にはならないので、直観にも合っていますね。
具体例3
政党数:5
各政党の議席数(計450議席)
政党A : 250
政党B:100
政党C:50
政党D:30
政党E:20
閾値:301(2/3以上)
具体例3はほぼ具体例2と同じですが、閾値が異なります。具体例2では過半数の226でしたが、具体例3では2/3以上の301にしてみました。この場合のシャープレイ・シュービック指数はどうなるでしょうか。
# プレイヤーの議席数
seats = {
"A" : 250,
"B" : 100,
"C" : 50,
"D" : 30,
"E" : 20,
}
# 閾値
threshold = 301
SS_index = compute_shapley_shubik_index(seats, threshold)
for party in seats:
print(f"政党{party}のS-S指数:{SS_index[party]}")
具体例2と違い、政党AのS-S指数は1より小さい値になりました。閾値が過半数から2/3以上になったことで、政党Aだけですべてを決められるわけじゃなくなったことをちゃんと反映できていますね。
ということで具体例2と3では結果がかなり異なりました。議席数が同じでも閾値が異なるだけでこんなに結果が変わるんですね。
おわりに
いかがでしたか。
今回の記事ではシャープレイ・シュービック指数をpythonで計算する方法について解説してみました。
今後もこのようなゲーム理論に関する記事を書いていきます!
最後までこの記事を読んでくれてありがとうございました。