こんにちは!しゅんです!
いきなりですが中学の数学を勉強すると下のような問題に出くわしますよね。
以下のデータについて第1四分位数、第2四分位数(中央値)、第3四分位数を求めなさい。
8人の生徒の数学のテストの点数
| 6点 | 7点 | 5点 | 2点 | 9点 | 5点 | 3点 | 1点 |
以下のデータについて第1四分位数、第2四分位数(中央値)、第3四分位数を求めなさい。
9人の生徒の数学のテストの点数
| 6点 | 7点 | 5点 | 2点 | 9点 | 5点 | 3点 | 1点 | 10点 |
以下のデータについて第1四分位数、第2四分位数(中央値)、第3四分位数を求めなさい。
10人の生徒の数学のテストの点数
| 6点 | 7点 | 5点 | 2点 | 9点 | 5点 | 3点 | 1点 | 10点 | 3点 |
以下のデータについて第1四分位数、第2四分位数(中央値)、第3四分位数を求めなさい。
11人の生徒の数学のテストの点数
| 6点 | 7点 | 5点 | 2点 | 9点 | 5点 | 3点 | 1点 | 10点 | 3点 | 8点 |
こんな問題を解くときに、データの値をそのまま答えるときと2つのデータの値を足して2で割る場合があってこんがらがりますよね。実はこの四分位数を求める問題は4つのパターンに分けられるんです。
この記事では4つのパターンそれぞれについて解き方を解説したいと思います!
4つのパターンに共通する解き方
問題の解き方を説明する前にまず4つの問題パターンに共通する解き方を説明します。説明が難しく感じた場合は最初に問題その1~問題その4の解き方を見てから戻ってくると理解しやすいと思います。
データを値が小さい順に並べて4等分する
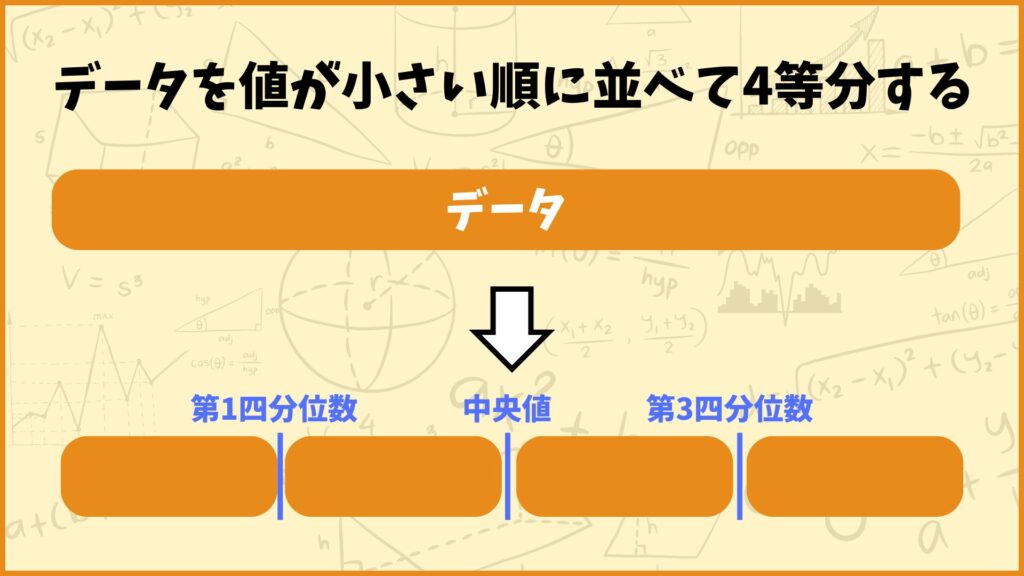
前提として上記のような四分位数を求める問題は共通して、
「データを値が小さい順に並べて4等分する」
というイメージを持って解くとと分かりやすいと思います。このとき4等分しているところを左から順番に第1四分位数、中央値(第2四分位数)、第3四分位数と呼びます。
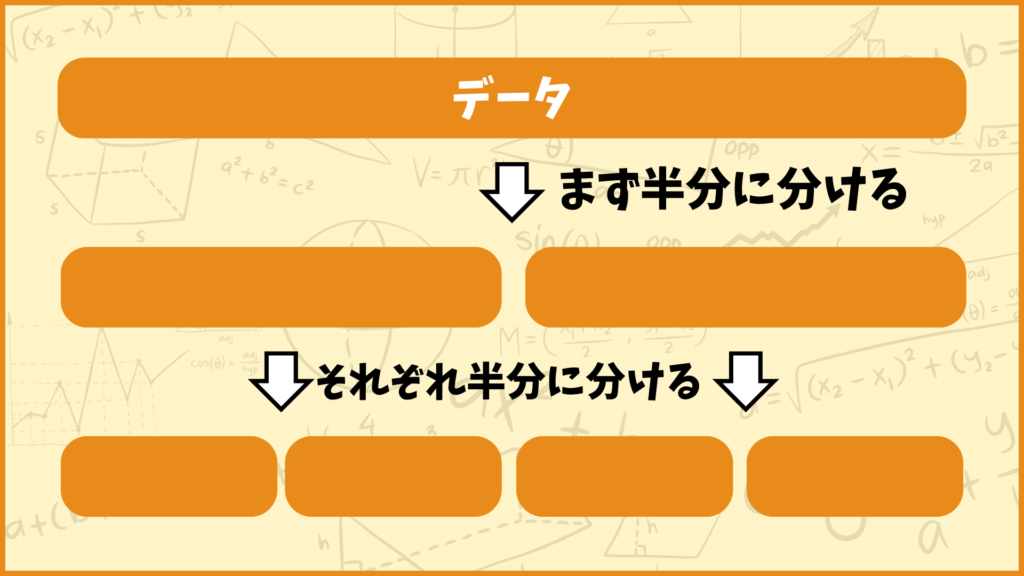
データを4等分するときはまず最初に2等分してから分けられたデータそれぞれをさらに2等分すると解きやすいと思います。
データの個数が偶数か奇数かで分けて考える
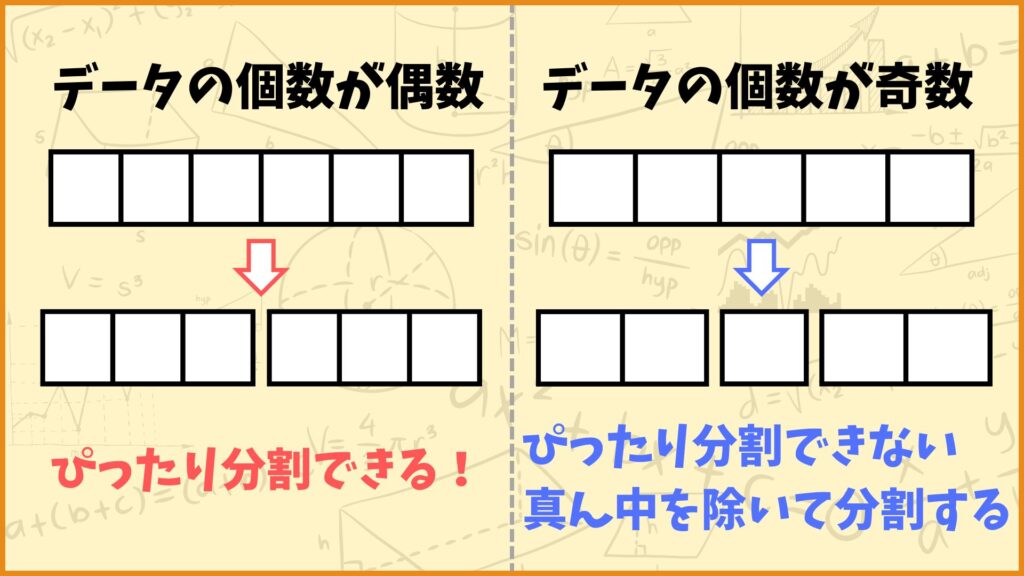
それでは次にデータを2等分するときのことを考えてみましょう。データの個数が偶数のときはピッタリ2分割できます。つまり左側のデータと右側のデータの個数が等しくになるようにデータを分割できます。
例えばデータの個数が6個の場合、3個ずつにデータを2等分することができます。
データの個数が偶数のとき分割した所の両隣のデータの平均値が四分位数となります。具体的な求め方はこのあと説明します。
一方データの個数が奇数のときはピッタリ2分割できません。つまり左側のデータと右側のデータの個数が等しくなるようにデータを分割することができません。
例えばデータの個数が5個の場合どう頑張っても3個と2個、1個と4個というようにデータを2等分することができません。
このような場合ちょうど真ん中のデータを基準にしてそれより左側のデータと右側のデータで分割しましょう。例えば以下のようなデータがあるとします。
| 1 | 2 | 3 | 4 | 6 |
このデータは個数が5個、つまり奇数なのでピッタリ2等分することができません。そこで真ん中のデータである3を基準にしてそれより左側と右側で分けましょう。
| 1 | 2 |
| 3 |
| 4 | 6 |
データの個数が奇数のときはこの基準となる真ん中のデータ値が四分位数となります。具体的な求め方はこのあと説明します。
問題その1を解く
以下のデータについて第1四分位数、第2四分位数(中央値)、第3四分位数を求めなさい。
8人の生徒の数学のテストの点数
| 6点 | 7点 | 5点 | 2点 | 9点 | 5点 | 3点 | 1点 |
それではまずデータを小さい順に並べてみましょう。
| 1点 | 2点 | 3点 | 5点 | 5点 | 6点 | 7点 | 9点 |
それでは次にデータを4等分しましょう。4等分するときはまず最初にデータを半分に分けてそれぞれをまた半分にすると解きやすいと思います。

このデータの個数は8個で偶数なのでちょうど左4つと右4つにデータを分けることができますね。
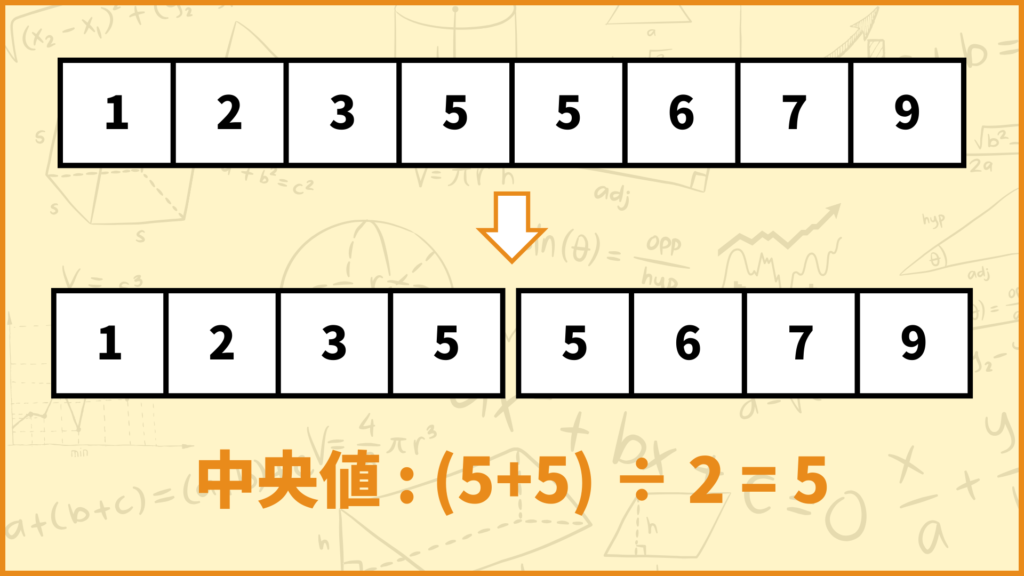
ということで上図のようにデータを2等分することができました。このとき中央値(第2四分位数)は分割した所の両隣のデータの平均値となります。両隣を見るとどっちも5なので中央値は
\(\frac{5 + 5}{2} = 5\)
と計算できます。それでは次に第1四分位数と第3四分位数を求めていきましょう。第1四分位数を求めるために左側のデータ、第3四分位数を求めるために右側のデータをそれぞれさらに2等分することを考えます。
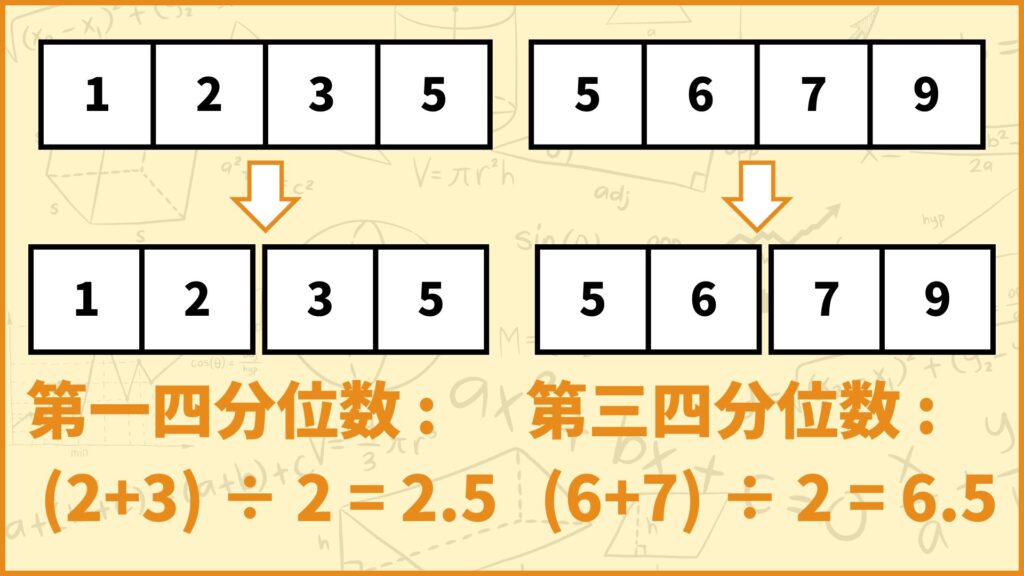
左側のデータも右側のデータもデータの個数が4つ、つまり偶数なのでピッタリ2等分することができます。データの個数が偶数なので四分位数は分割した所の両隣のデータの平均値となります。
第1四分位数に関して、分割したところの両隣のデータは2と3なので第1四分位数は
\(\frac{2+3}{2} = 2.5\)
と求められます。第3四分位数に関して、分割したところの両隣のデータは6と7なので第3四分位数は
\(\frac{6+7}{2} = 6.5\)
と求められます。
| 6点 | 7点 | 5点 | 2点 | 9点 | 5点 | 3点 | 1点 |
第1四分位数:2.5
中央値:5
第3四分位数:6.5
データの個数が8個の場合は中央値も第1、第3四分位数も両隣の値の平均値で計算しました。
問題その2を解く
以下のデータについて第1四分位数、第2四分位数(中央値)、第3四分位数を求めなさい。
9人の生徒の数学のテストの点数
| 6点 | 7点 | 5点 | 2点 | 9点 | 5点 | 3点 | 1点 | 10点 |
それではまずデータを小さい順に並べてみましょう。
| 1点 | 2点 | 3点 | 5点 | 5点 | 6点 | 7点 | 9点 | 10点 |
それでは次にデータを4等分しましょう。4等分するときはまず最初にデータを半分に分けてそれぞれをまた半分にすると解きやすいと思います。

このデータの個数は9個で奇数なのでピッタリデータを2等分することができません。こういうときはちょうど真ん中にあるデータを基準にしてそれより左側のデータと右側のデータで分割しましょう。
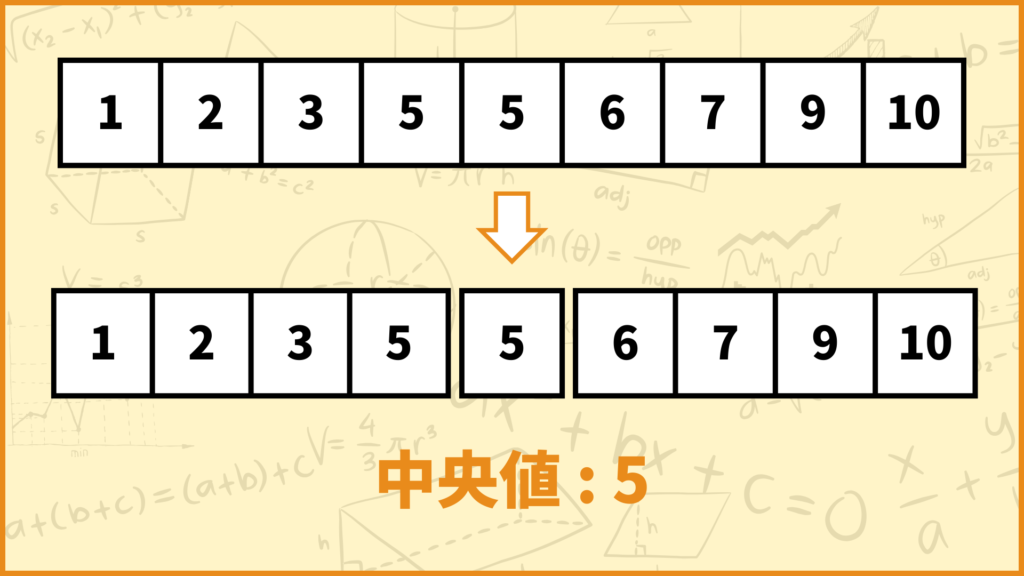
ということで上図のようにデータを2等分することができました。データの個数が奇数なので中央値(第二四分位数)はちょうど真ん中の値となるので中央値は5と求められます。
それでは次に第1四分位数と第3四分位数を求めていきましょう。第1四分位数を求めるために左側のデータ、第3四分位数を求めるために右側のデータをそれぞれさらに2等分することを考えます。
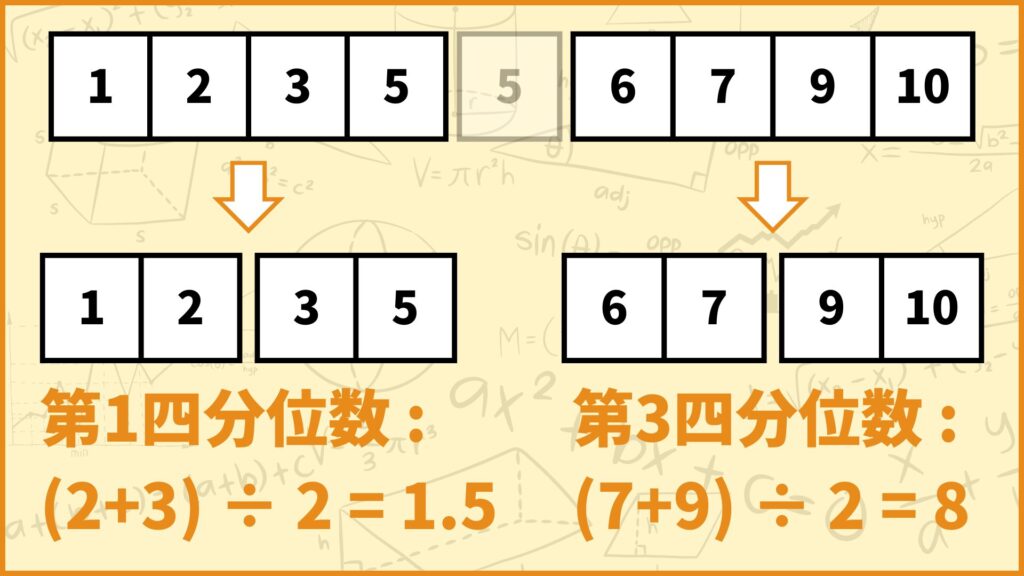
左側のデータも右側のデータもデータの個数が4つ、つまり偶数なのでピッタリ2等分することができます。データの個数が偶数なので四分位数は分割した所の両隣のデータの平均値となります。
このときちょうど真ん中のデータは無視して考えましょう。
第1四分位数に関して、分割したところの両隣のデータは2と3なので第1四分位数は
\(\frac{2+3}{2} = 2.5\)
と求められます。第3四分位数に関して、分割したところの両隣のデータは7と9なので第3四分位数は
\(\frac{7+9}{2} = 8\)
と求められます。
| 6点 | 7点 | 5点 | 2点 | 9点 | 5点 | 3点 | 1点 | 10点 |
第1四分位数:2.5
中央値:5
第3四分位数:8
データの個数が9個の場合は中央値はちょうど真ん中の値、第1、第3四分位数は両隣の値の平均値で計算しました。
問題その3を解く
以下のデータについて第1四分位数、第2四分位数(中央値)、第3四分位数を求めなさい。
10人の生徒の数学のテストの点数
| 6点 | 7点 | 5点 | 2点 | 9点 | 5点 | 3点 | 1点 | 10点 | 3点 |
それではまずデータを小さい順に並べてみましょう。
| 1点 | 2点 | 3点 | 3点 | 5点 | 5点 | 6点 | 7点 | 9点 | 10点 |
それでは次にデータを4等分しましょう。4等分するときはまず最初にデータを半分に分けてそれぞれをまた半分にすると解きやすいと思います。

このデータの個数は10個で偶数なのでちょうど左5つと右5つにデータを分けることができますね。
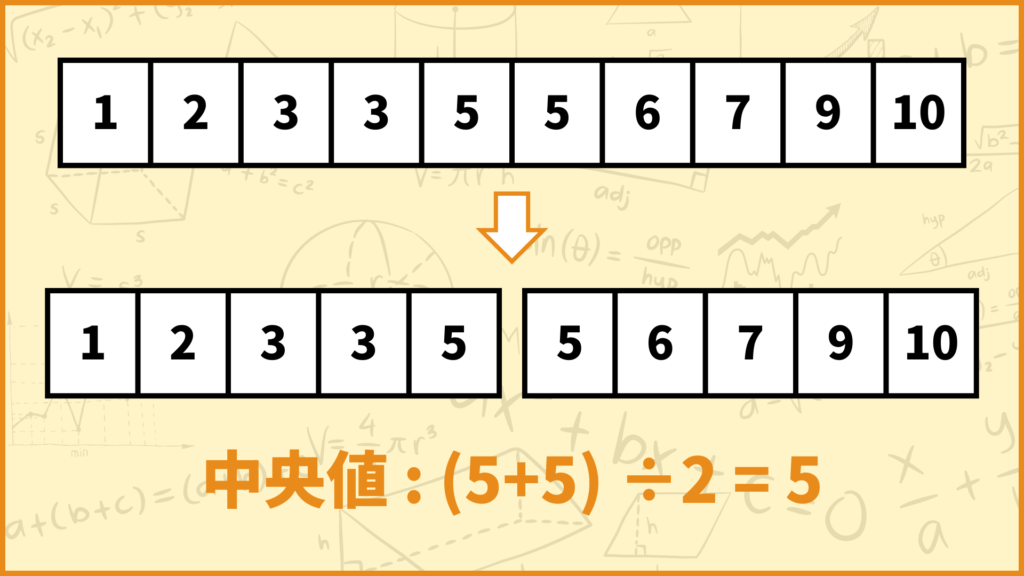
ということで上図のようにデータを2等分することができました。このとき中央値(第2四分位数)は分割した所の両隣のデータの平均値となります。両隣を見るとどっちも5なので中央値は
\(\frac{5 + 5}{2} = 5\)
と計算できます。それでは次に第1四分位数と第3四分位数を求めていきましょう。第1四分位数を求めるために左側のデータ、第3四分位数を求めるために右側のデータをそれぞれさらに2等分することを考えます。
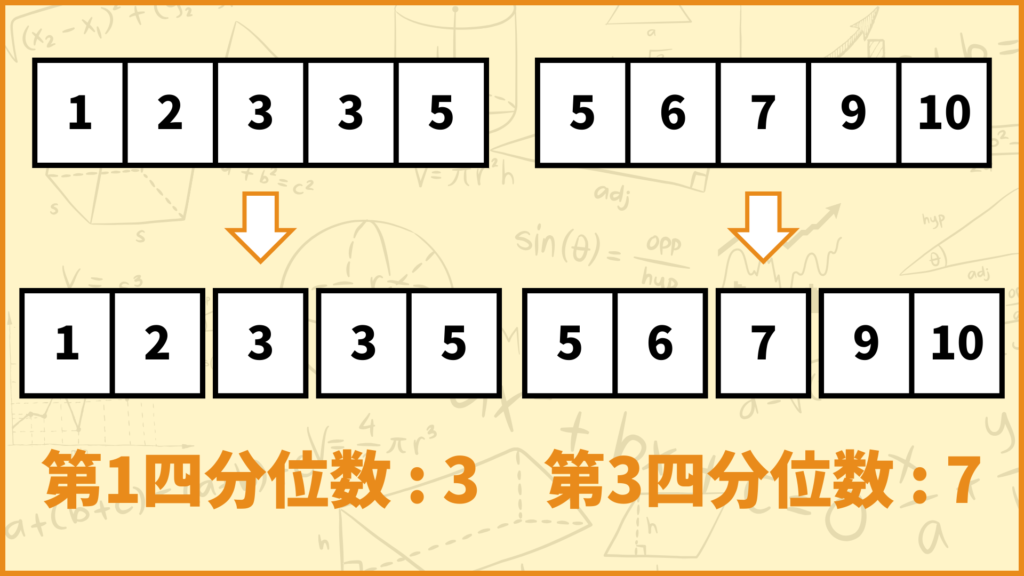
左側のデータも右側のデータもデータの個数が5つ、つまり奇数なのでピッタリ2等分することができません。そのためちょうど真ん中のデータを基準にしてそれより左側と右側で分割しましょう。
データの個数が奇数なので四分位数は基準にしたちょうど真ん中の値となります。ということで第1四分位数は3、第3四分位数は7と求められます。
| 6点 | 7点 | 5点 | 2点 | 9点 | 5点 | 3点 | 1点 | 10点 | 3点 |
第1四分位数:3
中央値:5
第3四分位数:7
データの個数が10個の場合は中央値は両隣の値の平均値、第1、第3四分位数はちょうど真ん中の値で計算しました。
問題その4を解く
以下のデータについて第1四分位数、第2四分位数(中央値)、第3四分位数を求めなさい。
11人の生徒の数学のテストの点数
| 6点 | 7点 | 5点 | 2点 | 9点 | 5点 | 3点 | 1点 | 10点 | 3点 | 8点 |
それではまずデータを小さい順に並べてみましょう。
| 1点 | 2点 | 3点 | 3点 | 5点 | 5点 | 6点 | 7点 | 8点 | 9点 | 10点 |
それでは次にデータを4等分しましょう。4等分するときはまず最初にデータを半分に分けてそれぞれをまた半分にすると解きやすいと思います。

このデータの個数は11個で奇数なのでピッタリデータを2等分することができません。こういうときはちょうど真ん中にあるデータを基準にしてそれより左側のデータと右側のデータで分割しましょう。
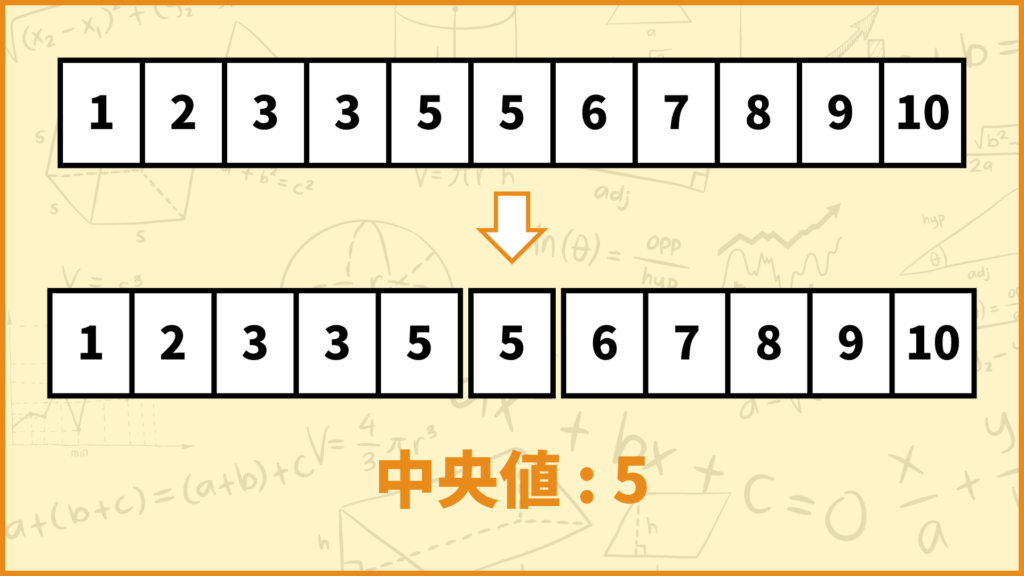
ということで上図のようにデータを2等分することができました。データの個数が奇数なので中央値(第二四分位数)はちょうど真ん中の値となるので中央値は5と求められます。
それでは次に第1四分位数と第3四分位数を求めていきましょう。第1四分位数を求めるために左側のデータ、第3四分位数を求めるために右側のデータをそれぞれさらに2等分することを考えます。
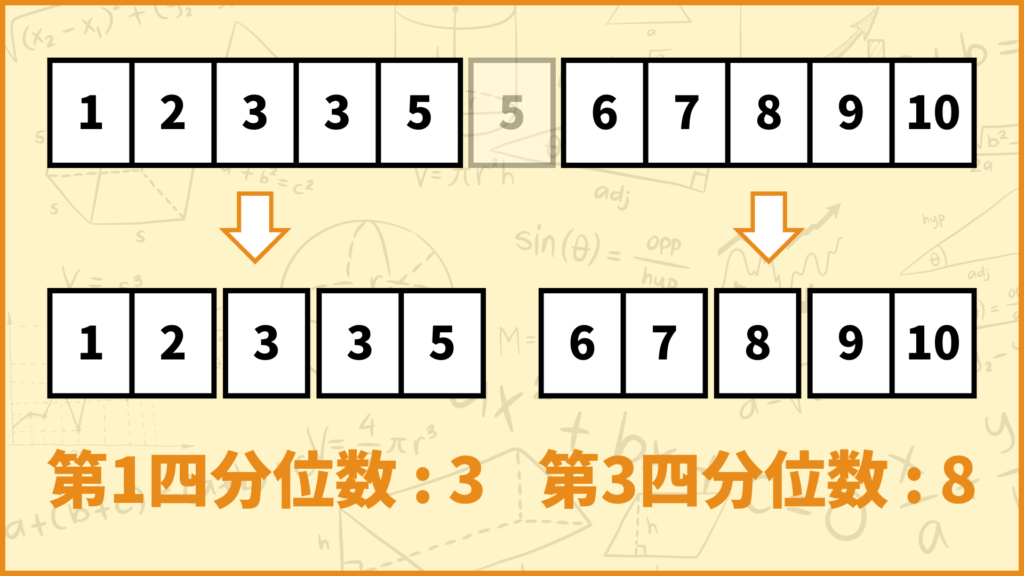
左側のデータも右側のデータもデータの個数が5つ、つまり奇数なのでピッタリ2等分することができません。そのためちょうど真ん中のデータを基準にしてそれより左側と右側で分割しましょう。
データの個数が奇数なので四分位数は基準にしたちょうど真ん中の値となります。ということで第1四分位数は3、第3四分位数は8と求められます。
| 6点 | 7点 | 5点 | 2点 | 9点 | 5点 | 3点 | 1点 | 10点 | 3点 | 8点 |
第1四分位数:3
中央値:5
第3四分位数:8
データの個数が11個の場合は中央値も第1、第3四分位数もちょうど真ん中の値で計算しました。
問題は4パターンに分けられる
ここまでは4つの問題それぞれについてどうやって四分位数を求めるかについて解説していきました。これらの問題を踏まえると四分位数の求め方は4パターンに分けられることが分かります。

なおこの表で言う「平均値を求める」はデータ数が偶数のとき四分位数を求める方法を表しており、「真ん中を選ぶ」はデータ数が奇数のとき四分位数を求める方法を表しています。
中央値を求める方法が2パターン、第1、第3四分位数を求める方法が2パターンあるので合計2×2=4パターンの求め方があります。今回の問題と照らし合わせると、
問題その1は中央値も第1、第3四分位数も平均値を求める
問題その2は中央値は真ん中を選び、第1、第3四分位数は平均値を求める
問題その3は中央値は平均値を求め、第1、第3四分位数は真ん中を選ぶ
問題その4は中央値も第1、第3四分位数も真ん中を選ぶ
という風になります。実はこれはデータの個数を4で割った時の余りと対応するんです。
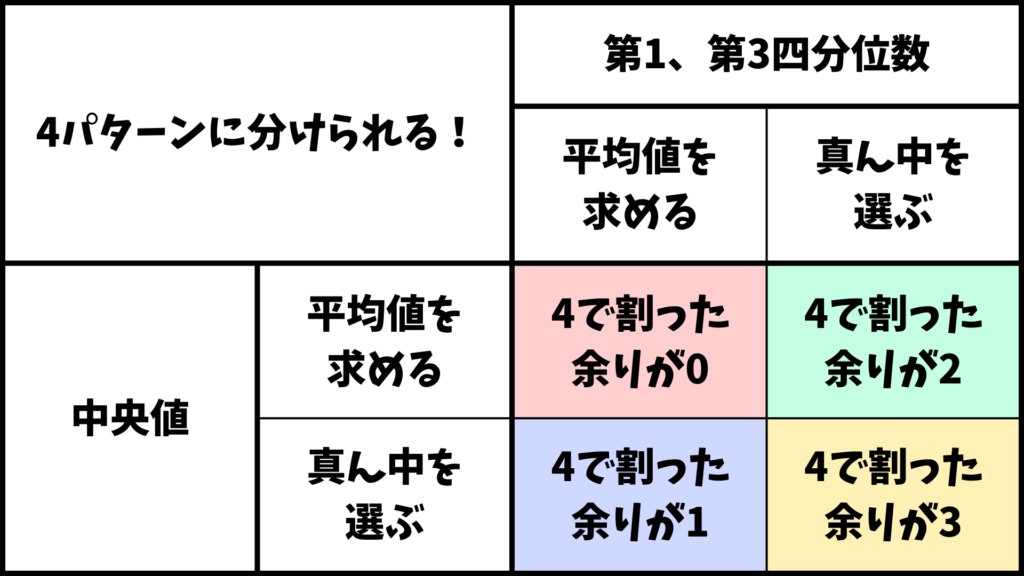
例えば問題1はデータの個数が8個なので4で割った余りが0です。このようにデータの個数を4で割った余りが0の場合中央値も第1、第3四分位数も平均値を求めて計算できます。これはデータの個数がもっと多くなっても同じように考えることができます。
ここからは少し難しい話になりますが、なぜ4で割った余りで分類できるのかを数式を使って考えてみましょう。なお\(n\)を0以上の整数とします。
パターン1:
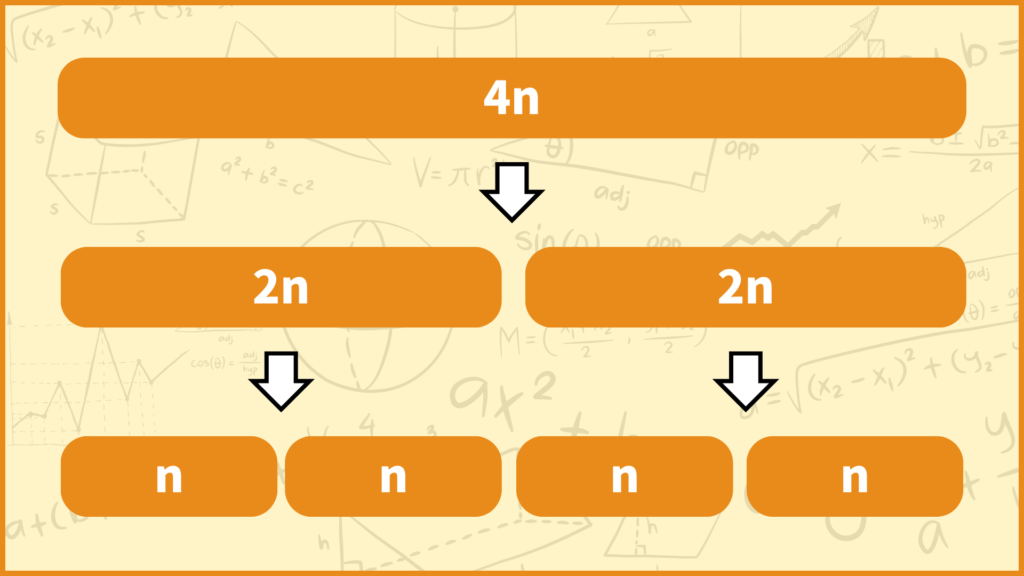
4で割った余りが0の数は\(4n\)と表せます。このとき\(4n\)は偶数なので中央値は「平均値を求める」という計算で求められます。
次に第1、第3四分位数について考えます。上記の操作によって左側と右側でそれぞれ\(2n\)ずつのデータに分けられました。\(2n\)は偶数なので第1、第3四分位数は「平均値を求める」という計算で求められます。(厳密に言うと\(n=0\)だと\(4n=0\)となるのでこのパターンだけは\(n>0\)と考えてください。)
パターン2
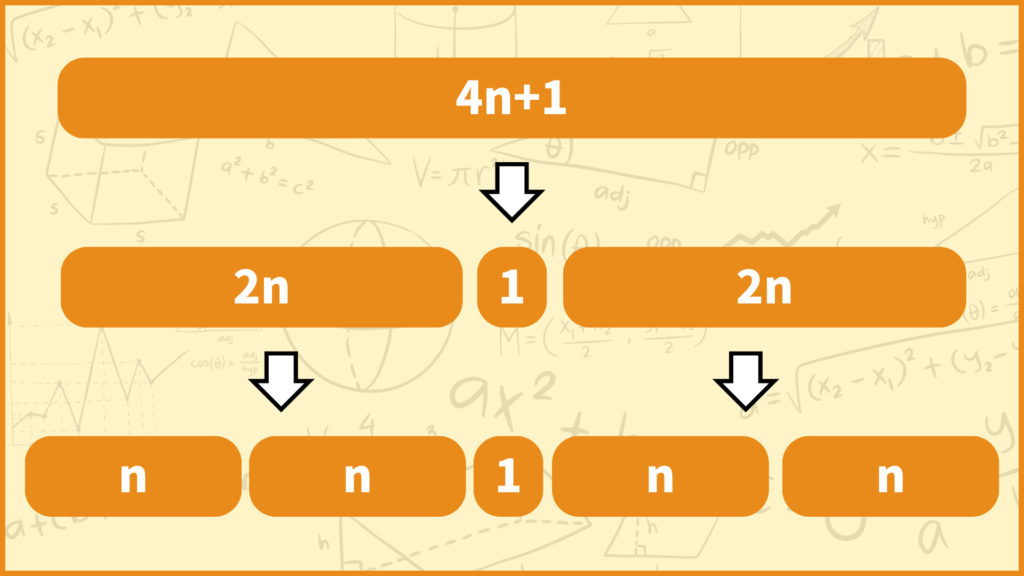
4で割った余りが1の数は\(4n+1\)と表せます。このとき\(4n+1\)は奇数なので中央値は「真ん中を選ぶ」という計算で求められます。
次に第1、第3四分位数について考えます。真ん中のデータは除いて考えるので左側と右側でそれぞれ\(2n\)個のデータに分けられました。\(2n\)は偶数なので第1、第3四分位数は「平均値を求める」という計算で求められます。
パターン3
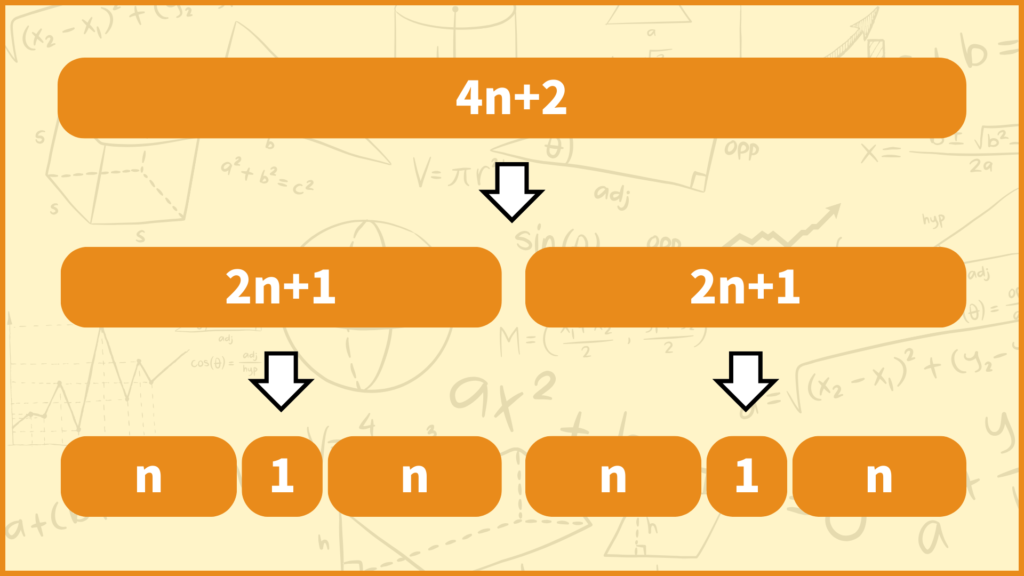
4で割った余りが2の数は\(4n+2\)と表せます。このとき\(4n+2\)は偶数なので中央値は「平均値を求める」という計算で求められます。
次に第1、第3四分位数について考えます。上記の操作によって左側と右側でそれぞれ\(2n+1\)ずつのデータに分けられました。\(2n+1\)は奇数なので第1、第3四分位数は「真ん中を選ぶ」という計算で求められます。
パターン4
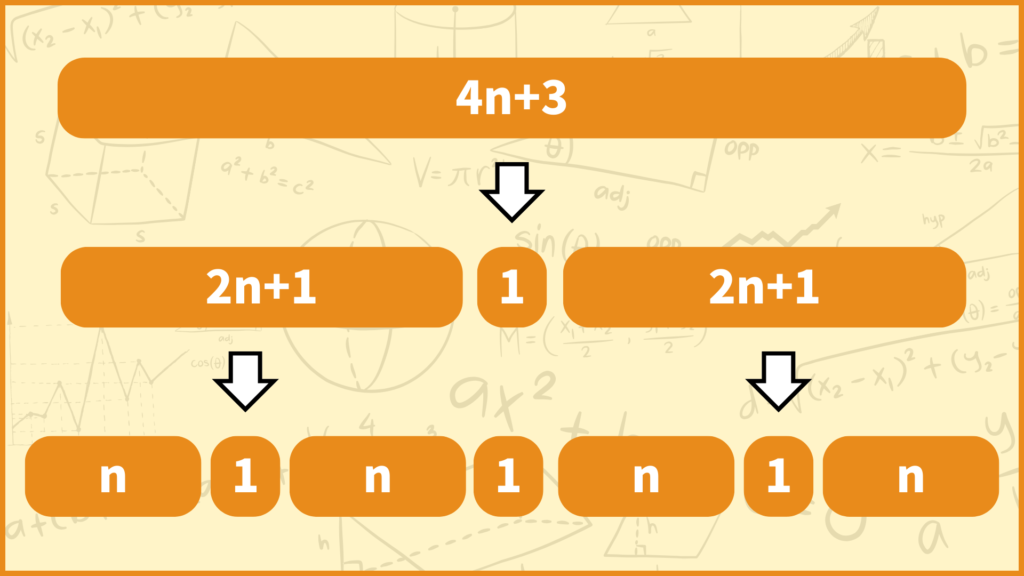
4で割った余りが3の数は\(4n+3\)と表せます。このとき\(4n+3\)は奇数なので中央値は「真ん中を選ぶ」という計算で求められます。
次に第1、第3四分位数について考えます。真ん中のデータは除いて考えるので左側と右側でそれぞれ\(2n+1\)個のデータに分けられました。\(2n+1\)は奇数なので第1、第3四分位数は「真ん中を選ぶ」という計算で求められます。
おわりに
いかがでしたか。
今回の記事では四分位数について解説していきました。
最後までこの記事を読んでくれてありがとうございました。
普段は大学数学の記事を書いてたりします。
ぜひ他の記事も読んでみてください!
このブログの簡単な紹介はこちらに書いてあります。
興味があったら見てみてください。
このブログでは経営工学を勉強している現役理系大学生が、経営工学に関することを色々話していきます!
ぼくが経営工学を勉強している中で感じたことや、興味深かったことを皆さんと共有出来たら良いなと思っています。
そもそも経営工学とは何なのでしょうか。Wikipediaによると
経営工学(けいえいこうがく、英: engineering management)は、人・材料・装置・情報・エネルギーを総合したシステムの設計・改善・確立に関する活動である。そのシステムから得られる結果を明示し、予測し、評価するために、工学的な分析・設計の原理・方法とともに、数学、物理および社会科学の専門知識と経験を利用する。
引用元 : 経営工学 – Wikipedia
長々と書いてありますが、要は経営、経済の課題を理系的な観点から解決する学問です。



