- スラック変数ってなに？
- スラック変数が表していることを図で理解したい…
こんにちは！しゅんです！
この記事ではシンプレックス法におけるスラック変数について説明します。
シンプレックス法は線形計画問題（LP）を効率的に解く方法の1つとして良く知られています。またスラック変数は線形計画問題のある不等式制約を等式制約にするために用いる変数です。
スラック変数は数式で理解できても具体的に何を表しているのか謎だな～って思ってたんですけど、なんとなく意味が分かった気がするので皆さんにもシェアしようかなと思います。
この記事では図を使って説明するために変数が2つの線形計画問題を使って説明します。またこの記事はシンプレックス法に登場する用語やシンプレックス法の手順が分かっている前提で書いています。そのため「基底変数」とか「実行可能基底解」のような用語の説明はしないです。
それではやっていきましょう！
普段は組合せ最適化の記事を書いてたりします。
ぜひ他の記事も読んでみてください！
このブログの簡単な紹介はこちらに書いてあります。
興味があったら見てみてください。
このブログでは経営工学を勉強している現役理系大学生が、経営工学に関することを色々話していきます！
ぼくが経営工学を勉強している中で感じたことや、興味深かったことを皆さんと共有出来たら良いなと思っています。
そもそも経営工学とは何なのでしょうか。Wikipediaによると
経営工学（けいえいこうがく、英: engineering management）は、人・材料・装置・情報・エネルギーを総合したシステムの設計・改善・確立に関する活動である。そのシステムから得られる結果を明示し、予測し、評価するために、工学的な分析・設計の原理・方法とともに、数学、物理および社会科学の専門知識と経験を利用する。
引用元 : 経営工学 – Wikipedia
長々と書いてありますが、要は経営、経済の課題を理系的な観点から解決する学問です。
説明で使う問題
\(\max \;\;\; 3x_1 + 2x_2\)
\(\;\text{s.t.}\;\;\;\; x_1 + 2x_2 \leq 10, \;\;\;\; \to ①\)
\(\;\;\;\;\;\;\;\;\;\; x_1 + x_2 \leq 6, \;\;\;\; \to ②\)
\(\;\;\;\;\;\;\;\;\;\; 2x_1 + x_2 \leq 10, \;\;\;\; \to ③\)
\(\;\;\;\;\;\;\;\;\;\; x_1 \geq 0, \;\;\;\; \to ④\)
\(\;\;\;\;\;\;\;\;\;\; x_2 \geq 0. \;\;\;\; \to ⑤\)
変数が2つなので2次元平面に図示することができます。制約式を図示すると以下のようになります。
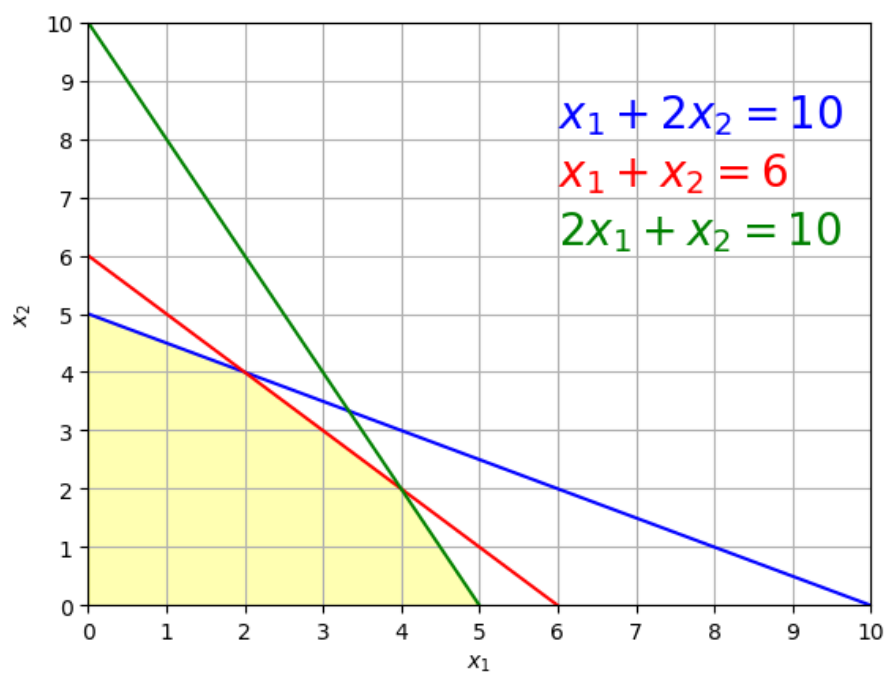
上図の黄色部分がこの問題の実行可能領域です。次にスラック変数 \(x_3,x_4,x_5\) を用いて不等式①,②,③を等式制約にしましょう。
\(\max \;\;\; 3x_1 + 2x_2\)
\(\;\text{s.t.}\;\;\;\; x_1 + 2x_2 + x_3 = 10, \;\;\;\; \to ①\)
\(\;\;\;\;\;\;\;\;\;\; x_1 + x_2 + x_4 = 6, \;\;\;\; \to ②\)
\(\;\;\;\;\;\;\;\;\;\; 2x_1 + x_2 + x_5 = 10, \;\;\;\; \to ③\)
\(\;\;\;\;\;\;\;\;\;\; x_1 \geq 0, \;\;\;\; \to ④\)
\(\;\;\;\;\;\;\;\;\;\; x_2 \geq 0, \;\;\;\; \to ⑤\)
\(\;\;\;\;\;\;\;\;\;\; x_3,x_4,x_5 \geq 0.\)
今回はこの \(x_3,x_4,x_5\) が何なのかを図で理解したいと思います。
スラック変数は境界にどれだけ近づけるかを表す
例えば式①について考えてみましょう。今 \((x_1,x_2) = (0,0)\) だとします。このとき \(x_3 = 10\) です。また、目的関数の係数はどちらも正なので、\(x_1,x_2\) を大きくすればするほど目的関数の値は大きくなります。
式①を見ればわかるように \(x_1,x_2\) の値が大きくなると \(x_3\) の値は小さくなります。\(x_1,x_2\) を \(x_1 + 2x_2 = 10\) を満たす値まで大きくする（例えば \((x_1,x_2) = (8,1)\)）と、\(x_3=0\) になりますが、\(x_3 \geq 0\) という制約があるのでこれ以上 \(x_1,x_2\) の値を大きくすることはできません。
つまり \(x_3\) は
境界 \(x_1 + 2x_2 = 10\) にどれだけ近づけるか
言い換えると不等式①を満たしながら後どれだけ \(x_1,x_2\) の値を大きくできるかということを表しています。
例えば \((x_1,x_2)=(0,0)\) から \(x_1,x_2\) を大きくして \((x_1,x_2) = (1,2)\) まで動かしたとします。このとき \(x_3\) は
\(1 + 2 \times 2 + x_3 = 10 \; \rightarrow \; x_3 = 5\)
となります。これは \((x_1,x_2)=(1,2)\) からさらに境界 \(x_1 + 2x_2 = 10\) に近づけようとするとき、後5だけ余裕があるみたいなイメージです。このとき上図のオレンジの両矢印の長さが\(\frac{1}{2}x_{3}=\frac{5}{2}\)となります。
オレンジの両矢印の長さが \(x_3\) じゃなくて \(\frac{1}{2}x_3\) なのは境界の直線の \(x_2\) の係数が2だからです。
ここから \(x_2=2\) に固定してさらに \(x_1\) だけを大きくしたときの両矢印の長さに注目してみましょう。\(x_1\)を大きくすると両矢印の長さ、すなわち\(x_3\)が小さくなっていることが上図から分かります。
最終的に \(x_1 = 6\) の所で境界上に点が位置します。このときの \(x_3\) の値を計算すると
\(6 + 2 \times 2 + x_3 = 10 \; \rightarrow \; x_3 = 0\)
となりちゃんと0になっていますね。このようにスラック変数 \(x_3\) は点 \((x_1,x_2)\) が後どれくらい境界 \(x_1 + 2x_2 = 10\) に近づけるかを表しています。
同じように考えると \(x_4\) は境界 \(x_1+x_2=6\)、\(x_5\) は境界 \(2x_1 + x_2 = 10\) に、それぞれ点 \((x_1,x_2)\) がどれくらい近づけるかを表していることが分かります。
以上のことを踏まえてこの問題に対してシンプレックス法を適用してみましょう。
シンプレックス法でこの問題を解いてみる
\(\max \;\;\; 3x_1 + 2x_2\)
\(\;\text{s.t.}\;\;\;\; x_1 + 2x_2 + x_3 = 10,\)
\(\;\;\;\;\;\;\;\;\;\; x_1 + x_2 + x_4 = 6,\)
\(\;\;\;\;\;\;\;\;\;\; 2x_1 + x_2 + x_5 = 10,\)
\(\;\;\;\;\;\;\;\;\;\; x_1,x_2,x_3,x_4,x_5 \geq 0.\)
それではスラック変数 \(x_3,x_4,x_5\) に着目してこの問題をシンプレックス法で解いてみましょう。
STEP.0
\(\max \;\;\; 3x_1 + 2x_2\)
\(\;\text{s.t.}\;\;\;\; x_3 = 10-x_1-2x_2,\)
\(\;\;\;\;\;\;\;\;\;\; x_4 = 6-x_1-x_2,\)
\(\;\;\;\;\;\;\;\;\;\; x_5 = 10-2x_1-x_2,\)
\(\;\;\;\;\;\;\;\;\;\; x_1,x_2,x_3,x_4,x_5 \geq 0.\)
制約式を辞書の形にしました。まず最初に \((x_1,x_2) = (0,0)\) と固定してみましょう。このとき \(x_3,x_4,x_5\) はそれぞれ
\(x_3 = 10\)
\(x_4 = 6\)
\(x_5 = 10\)
となります。つまりこのとき実行可能基底解は \((x_1,x_2,x_3,x_4,x_5)=(0,0,10,6,10)\)、目的関数値は0です。
目的関数の \(x_1,x_2\) の係数はどちらも正なので、目的関数の値を大きくするためには \(x_1,x_2\) のどっちかを大きくすれば良いです。シンプレックス法では1つの非基底変数だけ値を大きくして、他の非基底変数は0で固定します。
今回は \(x_1\) を固定して \(x_2\) を大きくしてみましょう。
このとき \(x_2\) をどこまで大きくできるか、スラック変数に着目して考えてみましょう。先ほど説明したようにスラック変数は境界に到達するまでの余裕を表しています。
例えば \(x_2=2\) にするとどうなるでしょう。スラック変数の値はそれぞれ
\(x_3 = 10-0-2 \times 2 = 6\)
\(x_4 = 6-0-2 = 4\)
\(x_5 = 10-0-2 = 8\)
となります。これを見ると分かるようにスラック変数の値が小さくなっていますが、いずれも正の値を取っています。つまりまだ\(x_2\)を大きくすることができます。
それではどこまで大きくできるのでしょうか。結論から言うと
基底変数の値が最初に0になるところまで
です。
ということで\(x_2\)をどんどん大きくしていった結果、\(x_2 = 5\) のところで \(x_3 = 0\) となりました。\(x_1=0\) と固定したままこれ以上 \(x_2\) を大きくすると、\(x_3\) が負の値になり実行可能領域の外に出てしまいます。
ということで \(x_2=5\) まで大きくした時点でこの操作を終了します。次に今行ったことを数式で書くとどうなるかを考えていきましょう。
\(x_3 = 10-2x_2=0 \Rightarrow x_2 = 5\)
\(x_4 = 6-x_2=0 \Rightarrow x_2 = 6\)
\(x_5 = 10-x_2=0 \Rightarrow x_2 = 10\)
\(x_1=0\) と固定したとき、各スラック変数が0を取るときの \(x_2\) の値を求めてみました。これを見ると、\(x_2\) をだんだん大きくしていくと \(x_3\) がまず最初に0になることが分かります。
\(x_2\)を大きくすることで目的関数値を上昇させることができるので、解を \((x_1,x_2,x_3,x_4,x_5)=(0,5,0,1,5)\) としましょう。
シンプレックス法では1つの基底変数と1つの非基底変数入れ替える操作を行いますが、それが上記の操作に対応します。基底変数 \(x_3\) と非基底変数 \(x_2\) を入れ替えましょう。それに伴って辞書も更新しましょう。
\(\max \;\;\; 10+2x_1-x_3\)
\(\;\text{s.t.}\;\;\;\; x_2 = 5 -\frac{1}{2}x_1 -\frac{1}{2}x_3,\)
\(\;\;\;\;\;\;\;\;\;\; x_4 = 1 – \frac{1}{2}x_1 + \frac{1}{2}x_3,\)
\(\;\;\;\;\;\;\;\;\;\; x_5 = 5 – \frac{3}{2}x_1 + \frac{1}{2}x_3,\)
\(\;\;\;\;\;\;\;\;\;\; x_1,x_2,x_3,x_4,x_5 \geq 0.\)
STEP.1
\(\max \;\;\; 10+2x_1-x_3\)
\(\;\text{s.t.}\;\;\;\; x_2 = 5-\frac{1}{2}x_1-\frac{1}{2}x_3,\)
\(\;\;\;\;\;\;\;\;\;\; x_4 = 1-\frac{1}{2}x_1 + \frac{1}{2}x_3,\)
\(\;\;\;\;\;\;\;\;\;\; x_5 = 5-\frac{3}{2}x_1 + \frac{1}{2}x_3,\)
\(\;\;\;\;\;\;\;\;\;\; x_1,x_2,x_3,x_4,x_5 \geq 0.\)
STEP.0で \((x_1,x_2)=(0,0)\) から \((x_1,x_2)=(0,5)\) にしました。\(x_2\) を大きくした影響で \(x_3=0\) となりました。STEP.0で求めたようにその他の変数の値は
\(x_4 = 1\)
\(x_5 = 5\)
となります。
これは辞書の右辺に\(x_1 = x_3 = 0\)を代入しても求めることができます。
このとき実行可能基底解は\((x_1,x_2,x_3,x_4,x_5)=(0,5,0,1,5)\)、目的関数値は10です。ではこれが最適解でしょうか。答えはNOです。それを理解するためには目的関数の係数を見る必要があります。
目的関数の係数は \(x_1\) が \(2\) で \(x_3\) が \(-1\) です。これは以下のことを表しています。
\(x_3\) を大きくしても目的関数値は大きくならないが、\(x_1\) を大きくすれば目的関数値は大きくなる。
ということで \(x_3=0\) と固定して \(x_1\) を大きくすることを考えます。
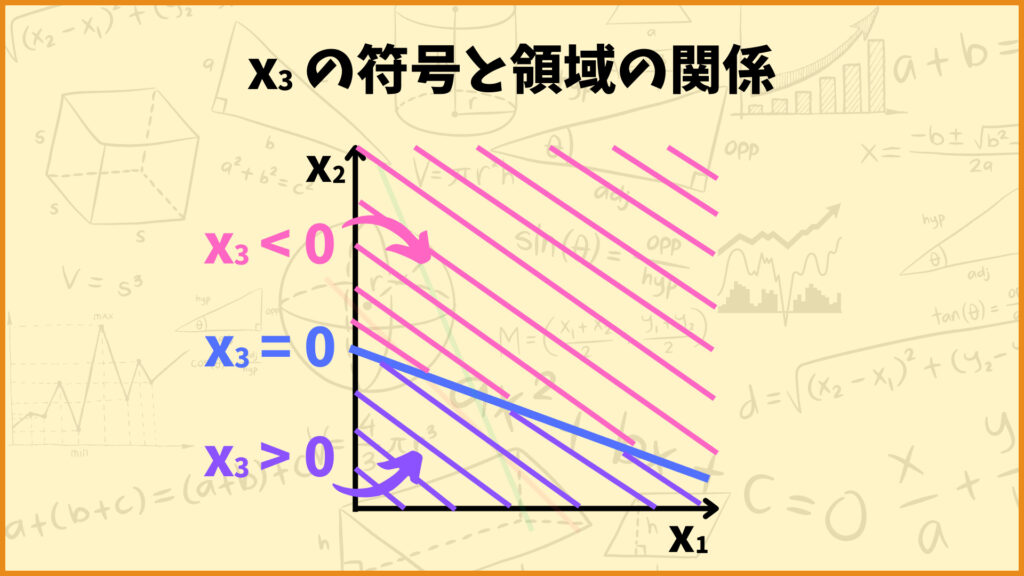
\(x_3=0\) を保ったままっていうのを図で理解してみましょう。\(x_3\) は不等式①のスラック変数で
\(x_3 = 10-x_1-2x_2\)
と表せます。つまり \(x_3=0\) は直線 \(x_1 + 2x_2 = 10\) を表します。図で言うと青い直線が \(x_3=0\) を表します。
同じように考えれば上図の紫色の領域が \(x_3 > 0\)、ピンク色の領域が \(x_3 <0\) を表すことが分かります。
つまり \(x_3 = 0\) を保ったまま \(x_1\) の値を大きくすることは
青い直線上で \(x_1\)の値を大きくしていく
ことを表します。
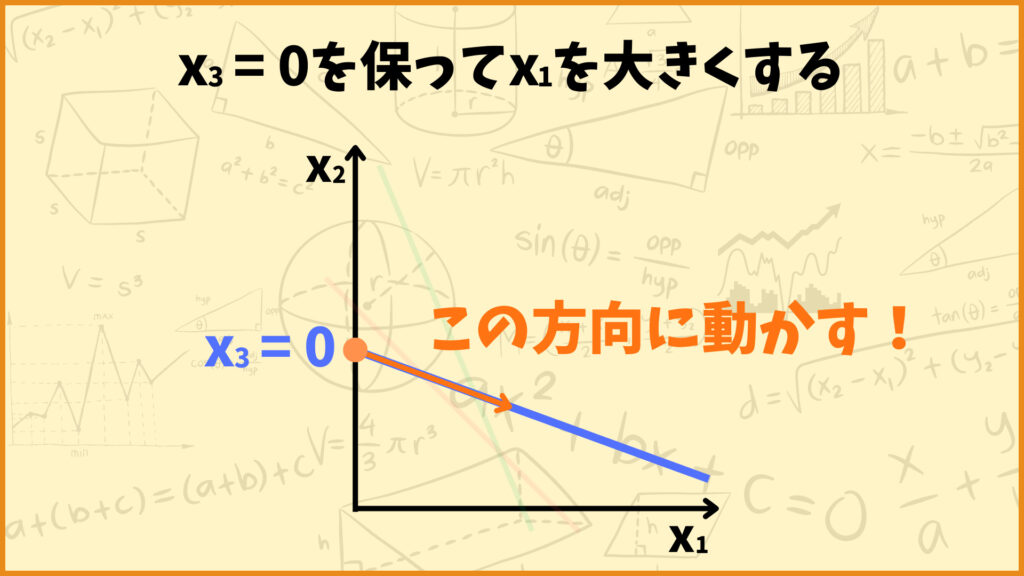
それでは \(x_1\) をどれくらいまで大きくすることができるでしょうか。結論から言うと非基底変数が最初に0になるところまでです。
\(x_1=2\) まで大きくしたところで上図の真ん中のグラフのように \(x_4=0\) となってしまいました。これはオレンジ色の点が赤い直線上に乗ったことを表しています。
これ以上 \(x_1\) を大きくしてしまうと \(x_4\) が負の値になってしまい非負制約に反して実行可能領域の外に出てしまいます。
上図を見ると分かるように \(x_1=2\) だと \(x_2,x_5\) はどちらも正の値を取っています。
\(x_2\) が0になるのは左のグラフの両矢印の長さが0になるところです。つまり青色の直線と \(x_1\) 軸が交わる \(x_1=10\) まで \(x_1\) を大きくすることができます。
\(x_5\) が0になるのは上図の右のグラフの両矢印の長さが0になるところです。つまり青色の直線と緑色の直線が交わる \(x_1=\frac{10}{3}\) まで \(x_1\) を大きくすることができます。
(このことは下で行っている計算からも確かめることができます。)
ということで \(x_1=2\) まで大きくした時点でこの操作を終了します。次に今行ったことを数式で書くとどうなるかを考えていきましょう。
\(x_2 = 5-\frac{1}{2}x_1=0 \Rightarrow x_1 = 10\)
\(x_4 = 1-\frac{1}{2}x_1=0 \Rightarrow x_1 = 2\)
\(x_5 = 5-\frac{3}{2}x_1=0 \Rightarrow x_1 = \frac{10}{3}\)
\(x_3=0\) と固定したとき、各スラック変数が0を取るときの \(x_1\) の値を求めてみました。これを見ると、\(x_1\) をだんだん大きくしていったときに \(x_4\) がまず最初に0になることが分かります。
\((x_1,x_3) = (2,0)\) のとき \((x_2,x_4,x_5)=(4,0,2)\) なので解を \((x_1,x_2,x_3,x_4,x_5)=(2,4,0,0,2)\) としましょう。
シンプレックス法の手順で1つの基底変数と1つの非基底変数入れ替える操作を行いましたが、それが上記の操作に対応します。基底変数 \(x_4\) と非基底変数 \(x_1\) を入れ替えましょう。それに伴って辞書も更新しましょう。
\(\max \;\;\; 14+x_3-4x_4\)
\(\;\text{s.t.}\;\;\;\; x_1 = 2 + x_3-2x_4,\)
\(\;\;\;\;\;\;\;\;\;\; x_2 = 4-x_3 + x_4,\)
\(\;\;\;\;\;\;\;\;\;\; x_5 = 2-x_3 + 3x_4,\)
\(\;\;\;\;\;\;\;\;\;\; x_1,x_2,x_3,x_4,x_5 \geq 0.\)
STEP.2
\(\max \;\;\; 14+x_3-4x_4\)
\(\;\text{s.t.}\;\;\;\; x_1 = 2 + x_3-2x_4,\)
\(\;\;\;\;\;\;\;\;\;\; x_2 = 4-x_3 + x_4,\)
\(\;\;\;\;\;\;\;\;\;\; x_5 = 2-x_3 + 3x_4,\)
\(\;\;\;\;\;\;\;\;\;\; x_1,x_2,x_3,x_4,x_5 \geq 0.\)
STEP.1で \((x_1,x_3)=(0,0)\) から \((x_1,x_3)=(2,0)\) にしました。\(x_1\) を大きくした影響で \(x_4=0\) となりました。STEP.1で求めたようにその他の変数の値は
\(x_2 = 4\)
\(x_5 = 2\)
となります。
これは辞書の右辺に \(x_3 = x_4 = 0\) を代入しても求めることができます。
このとき実行可能基底解は \((x_1,x_2,x_3,x_4,x_5)=(2,4,0,0,2)\)、目的関数値は14です。ではこれが最適解でしょうか。答えはNOです。それを理解するためには目的関数の係数を見る必要があります。
目的関数の係数は \(x_3\) が \(1\) で \(x_4\) が \(-4\) です。これは以下のことを表しています。
\(x_4\)を大きくしても目的関数値は大きくならないが、\(x_3\)を大きくすれば目的関数値は大きくなる。
ということで \(x_4=0\) と固定して \(x_3\) を大きくすることを考えます。
\(x_4=0\) を保ったままっていうのを図で理解してみましょう。\(x_4\) は不等式②のスラック変数で
\(x_4 = 6-x_1-x_2\)
と表せます。つまり \(x_4=0\) は直線 \(x_1 + x_2 = 6\) を表します。図で言うと赤い直線が \(x_4=0\) を表します。
同じように考えれば上図の紫色の領域が \(x_4 > 0\)、ピンク色の領域が \(x_4 <0\) を表すことが分かります。
つまり \(x_4 = 0\) を保ったまま \(x_3\) の値を大きくすると言うことは
赤い直線上で \(x_3\) の値を大きくしていく
と言うことを表します。では次に赤い直線に沿って右下と左上のどっちの方向に解を動かせばよいかを考えましょう。
上図の左側を見ると \(x_3<0,\;x_3=0,\;x_3>0\) の領域がそれぞれ図示されています。実行可能基底解は赤い直線と青い直線の交点であり、\(x_3\) の値を大きくするためには赤い直線上に沿って \(x_3>0\) の方向に動かせば良いです。
つまり上図のオレンジの矢印の方向に動かせば \(x_4=0\) を保ったまま\(x_3\)を大きくすることができます。
左上の方向に解を動かすと\(x_3\)が負の値になってしまいます。
それでは\(x_1\)をどれくらいまで大きくすることができるでしょうか。結論から言うと非基底変数が最初に0になるところまでです。これはグラフで理解するよりも前に数式で理解してみましょう。
\(x_1 = 2 + x_3=0 \Rightarrow x_3 = -2\)
\(x_2 = 4-x_3=0 \Rightarrow x_3 = 4\)
\(x_5 = 2-x_3=0 \Rightarrow x_3 = 2\)
\(x_4=0\) と固定したとき、各スラック変数が0を取るときの \(x_3\) の値を求めてみました。これを見ると、\(x_3\) をだんだん大きくしていったときに \(x_5\) がまず最初に0になることが分かります。
\(x_1\) に関しては \(x_3\) の値を大きくする限り \(x_1=0\) にはならないことが数式から分かります。図で考えても、右下方向に解を動かす限り \(x_1\) の値は大きくなり続けることが分かります。
次にこのことをグラフで理解してみましょう。
上図は \((x_3,x_4)=(2,0)\) のとき、変数 \(x_1,x_2,x_5\) がいくつかを表しています。これを見ると \(x_5=0\) となり、後の2つの変数はプラスの値を取っています。つまりまだ \(x_3\) を大きくする余裕があることを表しています。
これ以上 \(x_1\) を大きくしてしまうと \(x_4\) が負の値になってしまい、\(x_4\) の非負制約に反し実行可能領域の外に出てしまいます。
上図を見ると分かるように \(x_3=2\) だと \(x_1,x_2\) はどちらも正の値を取っています。
\(x_2\) が0になるのは真ん中のグラフのオレンジ色の両矢印の長さが0になるところです。つまり赤色の直線と \(x_1\) 軸が交わる \((x_1,x_2)=(6,0)\) まで \(x_3\) を大きくすることができます。\((x_1,x_2)=(6,0)\) のときの \(x_3\) の値を計算すると \(x_3=10-6-2 \times 0 = 4\) となります。
\(x_1\) が0になるのは右のグラフのオレンジ色の両矢印の長さが0になるところです。つまり赤色の直線と \(x_2\) 軸が交わる \((x_1,x_2)=(0,6)\) まで \(x_3\) を大きくすることができます。\((x_1,x_2)=(0,6)\) のときの \(x_3\) の値を計算すると \(x_3=10-0-2 \times 6 = -2\) となります。
(さきほど数式から導いた値と同じになっていますね。)
\((x_3,x_4) = (2,0)\) のとき \((x_1,x_2,x_5)=(4,2,0)\) なので解を \((x_1,x_2,x_3,x_4,x_5)=(4,2,2,0,0)\) としましょう。
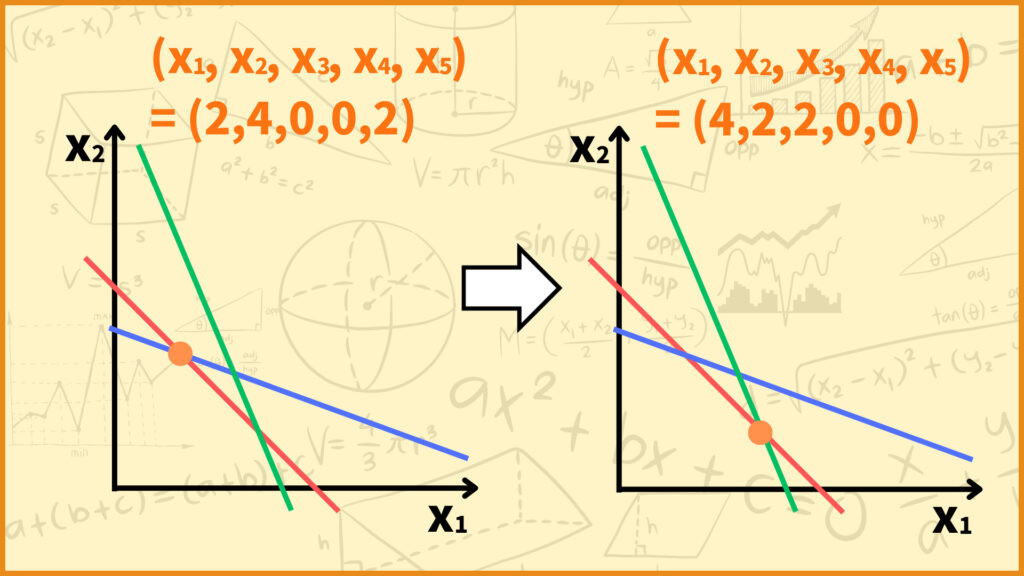
シンプレックス法の手順で1つの基底変数と1つの非基底変数入れ替える操作を行いましたが、それが上記の操作に対応します。基底変数 \(x_3\) と非基底変数 \(x_5\) を入れ替えましょう。それに伴って辞書も更新しましょう。
\(\max \;\;\; 16-x_4-x_5\)
\(\;\text{s.t.}\;\;\;\; x_1 = 4 + x_4-x_5,\)
\(\;\;\;\;\;\;\;\;\;\; x_2 = 2-2x_4 + x_5,\)
\(\;\;\;\;\;\;\;\;\;\; x_3 = 2 + 3x_4-x_5,\)
\(\;\;\;\;\;\;\;\;\;\; x_1,x_2,x_3,x_4,x_5 \geq 0.\)
目的関数の係数が全て負なので終了
\(\max \;\;\; 16-x_4-x_5\)
\(\;\text{s.t.}\;\;\;\; x_1 = 4 + x_4-x_5,\)
\(\;\;\;\;\;\;\;\;\;\; x_2 = 2-2x_4 + x_5,\)
\(\;\;\;\;\;\;\;\;\;\; x_3 = 2 + 3x_4-x_5,\)
\(\;\;\;\;\;\;\;\;\;\; x_1,x_2,x_3,x_4,x_5 \geq 0.\)
目的関数の係数が全て負になりましたね。これは以下のことを表しています。
\(x_4\) を大きくしても \(x_5\) を大きくしても目的関数値は大きくならない。
ということでこの時点でシンプレックス法を終了します。最適解は \((x_1,x_2,x_3,x_4,x_5) = (4,2,2,0,0)\) で最適値は16となります。
ちなみに最適解では \(x_4,x_5\) の値が0となっています。式②と式③にそれぞれ\(x_4=0\)と\(x_5=0\)を代入すると
\(x_1+x_2=6\)
\(2x_1+x_2=10\)
となります。これはそれぞれ図の赤い直線と緑の直線の方程式となっています。つまり \(x_4=x_5=0\) は赤い直線と緑の直線の交点だということを表しています。
おわりに
いかがでしたか。
今回の記事ではスラック変数について解説していきました。
今後もこのような数理最適化に関する記事を書いていきます！
最後までこの記事を読んでくれてありがとうございました。
参考文献
梅谷俊治. しっかり学ぶ数理最適化 モデルからアルゴリズムまで. 講談社, 2020, 368p.
