こんにちは!しゅんです!
今回の記事では歪度について説明していきたいと思います!
歪度は統計やデータ分析を勉強するときに登場する数学用語です。この記事では歪度がいったい何を表しているのか、どうやって計算するのかを1つずつ丁寧に説明していきます!
今回のテーマは
・手計算で歪度を求める ← 今回はこっち!
・pythonで歪度を求める
の2部構成になっています!
pythonで歪度を求める方を解説している記事はこちらです!
それではやっていきましょう!
普段は統計検定2級の記事を書いてたりします。
ぜひ他の記事も読んでみてください!
このブログの簡単な紹介はこちらに書いてあります。
興味があったら見てみてください。
このブログでは経営工学を勉強している現役理系大学生が、経営工学に関することを色々話していきます!
ぼくが経営工学を勉強している中で感じたことや、興味深かったことを皆さんと共有出来たら良いなと思っています。
そもそも経営工学とは何なのでしょうか。Wikipediaによると
経営工学(けいえいこうがく、英: engineering management)は、人・材料・装置・情報・エネルギーを総合したシステムの設計・改善・確立に関する活動である。そのシステムから得られる結果を明示し、予測し、評価するために、工学的な分析・設計の原理・方法とともに、数学、物理および社会科学の専門知識と経験を利用する。
引用元 : 経営工学 – Wikipedia
長々と書いてありますが、要は経営、経済の課題を理系的な観点から解決する学問です。
歪度ってなに?
まず初めに歪度をザックリ説明すると
データの分布がどれだけ偏っているかを表す指標
です。と言っても言葉だけでは説明してもよくわからないので具体的なグラフを使って説明したいと思います。
グラフを使って歪度を理解する

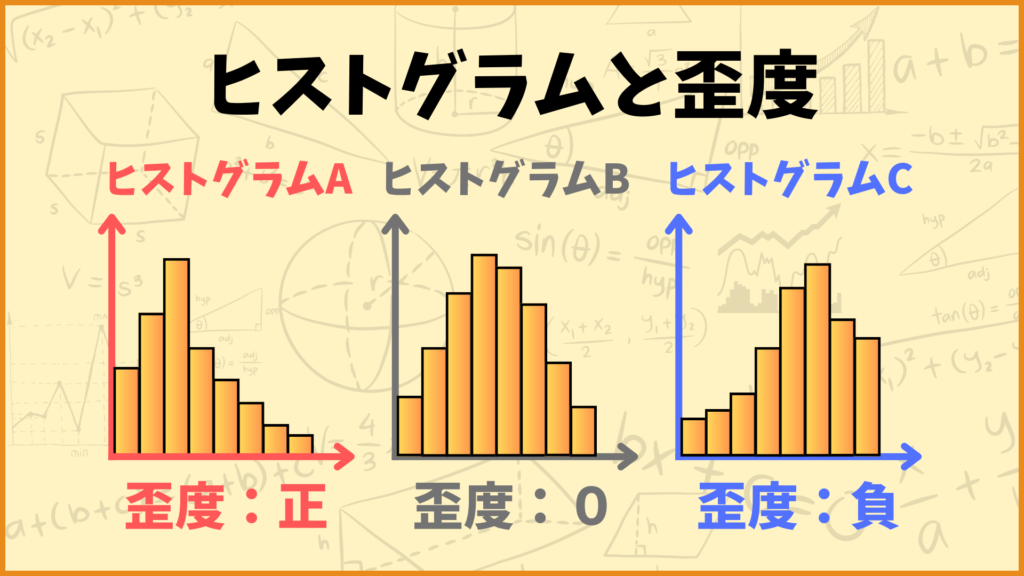
上にある3つのヒストグラムについて考えてみましょう。この3つのヒストグラムはデータの偏り具合が全然違いますね。
ヒストグラムA:データの分布が左に偏っている
ヒストグラムB:データの分布が偏っていない(左右対称)
ヒストグラムC:データの分布が右に偏っている
まずヒストグラムAを見てみましょう。これを見るとデータが結構左側に偏っていますね。例えばこのヒストグラムがテストの点数分布だとしましょう。横軸が点数、縦軸が人数のヒストグラムだと考えると、このテストは結構みんな点数が取れなかったのかなと推測できます。テストが結構難しかったのかなと分析できますね。
次にヒストグラムBを見てみましょう。これを見るとデータは特に偏っておらず、ほぼ左右対称な分布になっています。これもテストの点数分布だと思って考えてみましょう。ヒストグラムBの場合はいい感じにテストの点数が散らばっています。おそらくこのテストは難しすぎず簡単すぎずちょうど良い感じのテストだったんだと推測できます。
最後にヒストグラムCを見てみましょう。これを見るとデータが結構右側に偏っていますね。これもヒストグラムがテストの点数分布だとして考えましょう。このテストは結構みんな点数が取れたのかなと推測できます。テストが結構簡単だったのかなと分析できますね。
このように分布の偏り具合はデータがどういうものかを知る上で非常に重要なんです。
そしてこの偏り具合をちゃんと数値化したものが歪度になります。
3つのヒストグラムとそれらの歪度
それでは3つのヒストグラムとそれらの歪度について見ていきましょう。
分布が左に偏っている(ヒストグラムA):歪度は正の値を取る
分布が偏っていない(ヒストグラムB):歪度は0に近い値を取る
分布が右に偏っている(ヒストグラムC):歪度は負の値を取る
データの分布が左側に偏っていると歪度の値は正の値を取ります。左に偏れば偏るほどその値はどんどん大きくなります。
一方データの分布が右側に偏っていると歪度の値は負の値になります。右に偏れば偏るほどその値はどんどん小さくなります。
データの分布に偏りが無くなれば無くなるほど0に近くなります。分布が完全に左右対称になると歪度は0を取ります。
歪度を求める式
結論歪度を求める式は以下のようになります。
歪度 = \(\frac{E[(X-\mu)^3]}{\sigma^3}\)
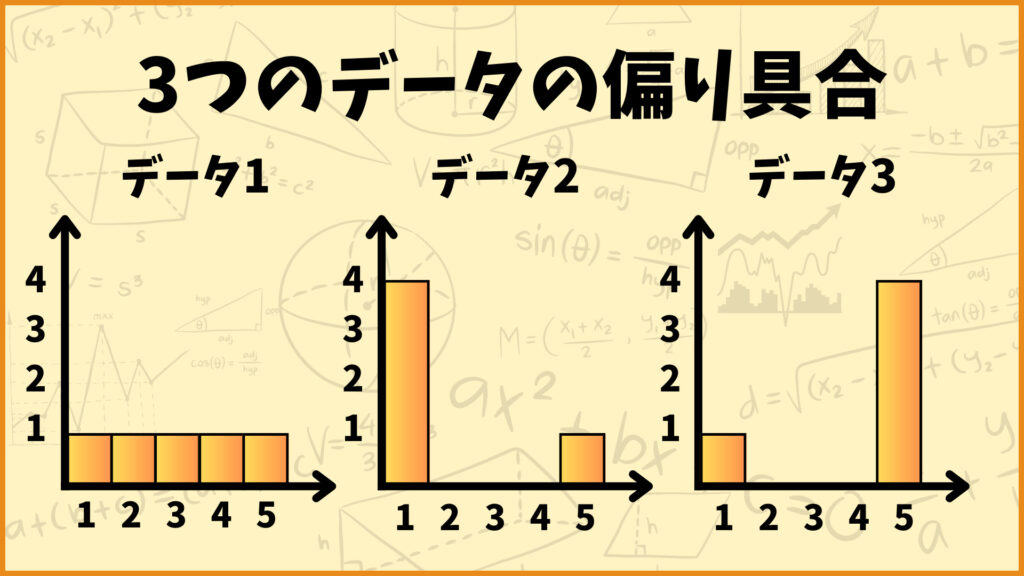
計算式だけ見ても何なのか分かりづらいと思うので、具体的なデータを使って歪度を求めてみましょう。今回はこの下にある3つのデータの歪度を求めていこうと思います。
少し専門的な話
今回は分かりやすいので標本歪度の説明をしたいと思います。つまりこの3つのデータをそれぞれ標本だと考えて、歪度を\(\frac{\frac{1}{n}\sum\limits^n_{i=1}(x_i – \bar{x})^3}{s^3}\)として計算したいと思います。
(\(s\)は標本標準偏差)
説明に用いるデータの説明

データ1は1から5まで満遍なく数値があります。ヒストグラムにすると左右対称になるのでおそらく歪度は0になるはずです。
データ2は4つが1、1つが5になっています。ヒストグラムにすると左側に偏っているのでおそらく歪度は正の値になるはずです。
データ3は4つが5、1つが1になっています。ヒストグラムにすると右側に偏っているのでおそらく歪度は負の値になるはずです。
データ1の歪度を求める
まず初めにデータ1の歪度を求めていきます。まずこのデータの平均は\(\bar{x}=3\)なので\(x_i-\bar{x}\)は左から順に-2, -1, 0, 1, 2となります。
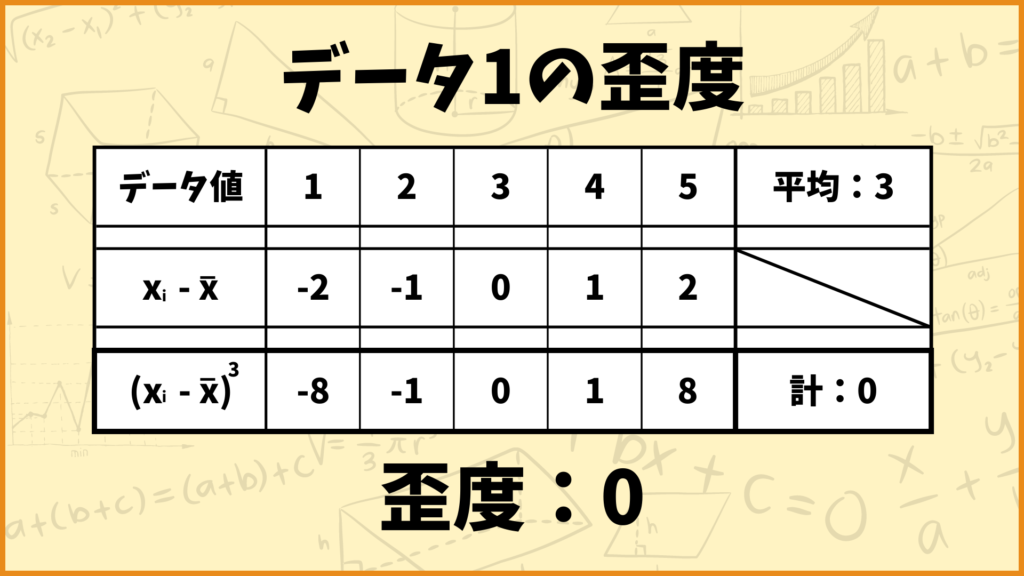
このとき\(\sum\limits^5_{i=1}(x_i-\bar{x})^3=0\)となります。したがって(標本)歪度の分子が0になるので、(標本)歪度の値も0となります。
これでデータ1の分布が左右対称だったと言うことが分かりました。
データ2の歪度を求める
次にデータ2の歪度を求めていきます。データ1のように簡単には計算できないので、1つずつ解説していきます。
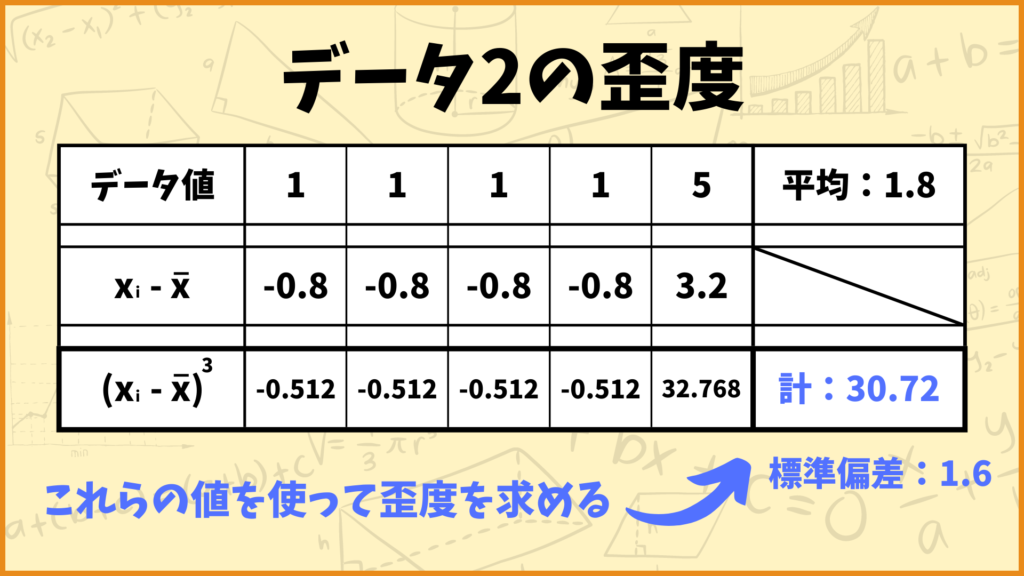
まずデータ1の平均から求めましょう。平均値は以下のように求められます。
\(\bar{x} = \frac{1+1+1+1+5}{5}=1.8\)
次にデータ2の(標本)標準偏差を求めましょう。標準偏差を求めるにはまず最初に分散を求めてそれのルートの値を求めればOKです。
分散:
\(s^2 = \frac{(1-1.8)^2+(1-1.8)^2+(1-1.8)^2+(1-1.8)^2+(5-1.8)^2}{5} = 2.56\)
標準偏差:
\(s = \sqrt{2.56}=1.6\)
次に\(\frac{1}{5}\sum\limits^5_{i=1}(x_i-\bar{x})^3\)の値を求めていきます。さっきの画像で全ての\(i=1,2,…,5\)に対して\((x_i-\bar{x})^3\)の値を求めているので、それを5で割りましょう。
\(\frac{1}{5}\sum\limits^5_{i=1}(x_i-\bar{x})^3=\frac{1}{5}×30.72=6.144\)
最後に歪度を求めましょう。歪度は今求めた\(\frac{1}{5}\sum\limits^5_{i=1}(x_i-\bar{x})^3\)を標準偏差の3乗\(s^3\)で割ります。
歪度:
\(\frac{6.144}{1.6^3}=1.5\)
ということでデータ2の歪度が1.5であることが分かりました。この値を見るとデータの分布が左側に偏っていることが分かりますね。
データ3の歪度を求めてみよう
最後にデータ3の歪度を求めてみます。皆さんも自分で計算してみてください。
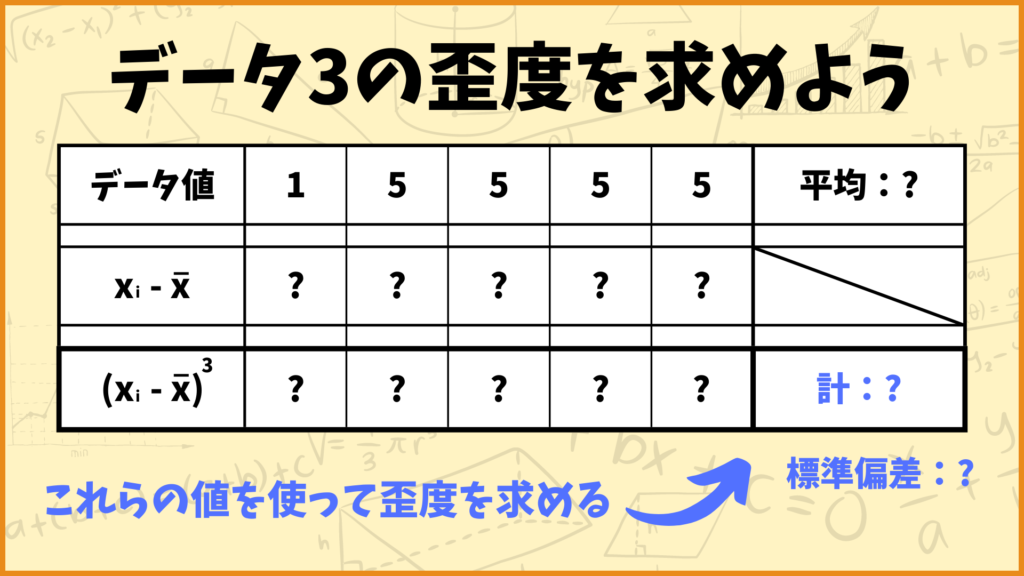
\(\bar{x}=\frac{1+5+5+5+5}{5}=4.2\)
分散:
\(s^2 = \frac{(1-4.2)^2+(5-4.2)^2+(5-4.2)^2+(5-4.2)^2+(5-4.2)^2}{5} = 2.56\)
標準偏差:
\(s = \sqrt{2.56}=1.6\)
\(\frac{1}{5}\sum\limits^5_{i=1}(x_i-\bar{x})^3\)
\(=\frac{1}{5}\{(1-4.2)^3+(5-4.2)^3+(5-4.2)^3+(5-4.2)^3+(5-4.2)^3\}\)
\(=\frac{1}{5}×(-30.72)\)
\(=-6.144\)
歪度:
\(\frac{-6.144}{1.6^3}=-1.5\)
ということで歪度を計算することができました。歪度の値が負なのでやはりデータ3の分布は右側に偏っているということが分かりました。
またデータ2の歪度と比べてみると、プラスマイナスだけ違くて数値自体は同じ値になっていますね。

データ2とデータ3の分布は鏡合わせのような関係になっていますね。このような分布の場合は歪度の絶対値は同じでプラスマイナスの値だけ変わるんですね。
考えてみれば偏り具合はどっちも同じですからね。後はどっち側に偏ているかによってプラスマイナスの値が決まると言う感じで、ちゃんと分布の偏り具合を反映できていそうです。
おわりに
いかがでしたか。
今回の記事では歪度の公式について解説していきました。
今後もこのような統計に関する記事を書いていきます!
最後までこの記事を読んでくれてありがとうございました。