こんにちは!しゅんです!
いきなりですが皆さんは歪度と尖度を知っていますか?
歪度と尖度は統計で勉強する概念で、データの分布を知る上で重要な指標になります。ぼくも最近統計検定の勉強をしていて学んだので皆さんにもシェアしたいと思います!
今回は説明と一緒にNBAのデータを使ってどんなものか確かめたいと思います。
それでは解説していきましょう!
この記事は前回からの続きなので前回までの記事を見ると分かりやすいです!
このブログでは経営工学を勉強している現役理系大学生が、経営工学に関することを色々話していきます!
ぼくが経営工学を勉強している中で感じたことや、興味深かったことを皆さんと共有出来たら良いなと思っています。
そもそも経営工学とは何なのでしょうか。Wikipediaによると
経営工学(けいえいこうがく、英: engineering management)は、人・材料・装置・情報・エネルギーを総合したシステムの設計・改善・確立に関する活動である。そのシステムから得られる結果を明示し、予測し、評価するために、工学的な分析・設計の原理・方法とともに、数学、物理および社会科学の専門知識と経験を利用する。
引用元 : 経営工学 – Wikipedia
長々と書いてありますが、要は経営、経済の課題を理系的な観点から解決する学問です。
ヒストグラムとは
歪度と尖度を説明する前にまずはヒストグラムについて簡単に解説します!
ヒストグラムはデータの分布を分かりやすく図に表したものです。
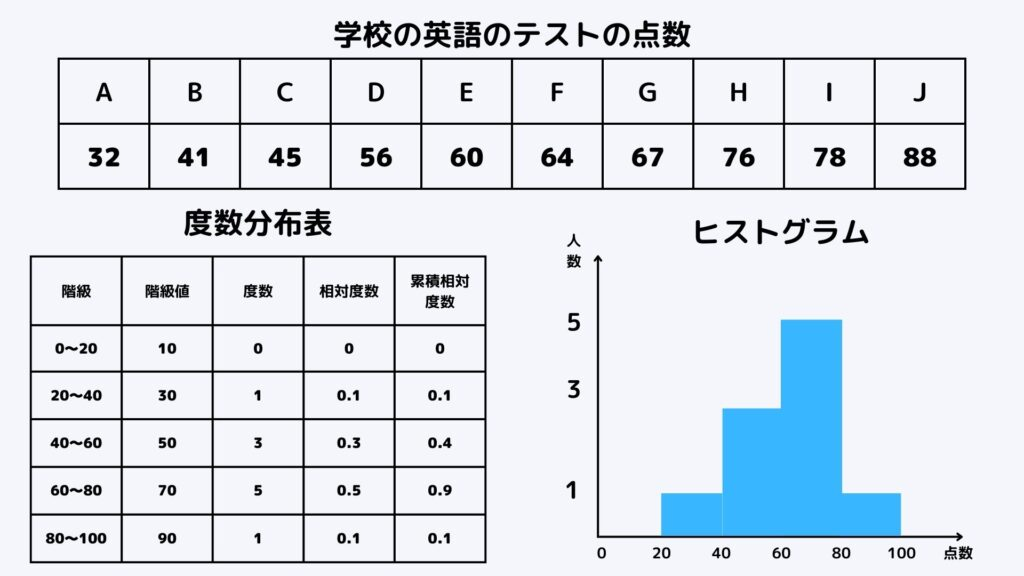
ヒストグラムは上図のようになります。基本的にはデータから度数分布表を作ってそこからヒストグラムを作るという流れです。
ヒストグラムを見ればある範囲にどれだけデータが集中しているかの分布を知ることができます。視覚的にも分かりやすいので非常に便利です。
詳しくはこちらの記事で解説しているのでぜひ読んでみてください!
歪度とは
歪度はヒストグラム(データの分布)が左右対称かどうかを表す指標です。
・0のとき : 左右対称
・0より大きいとき : 左に偏る
・0より小さいとき : 右に偏る
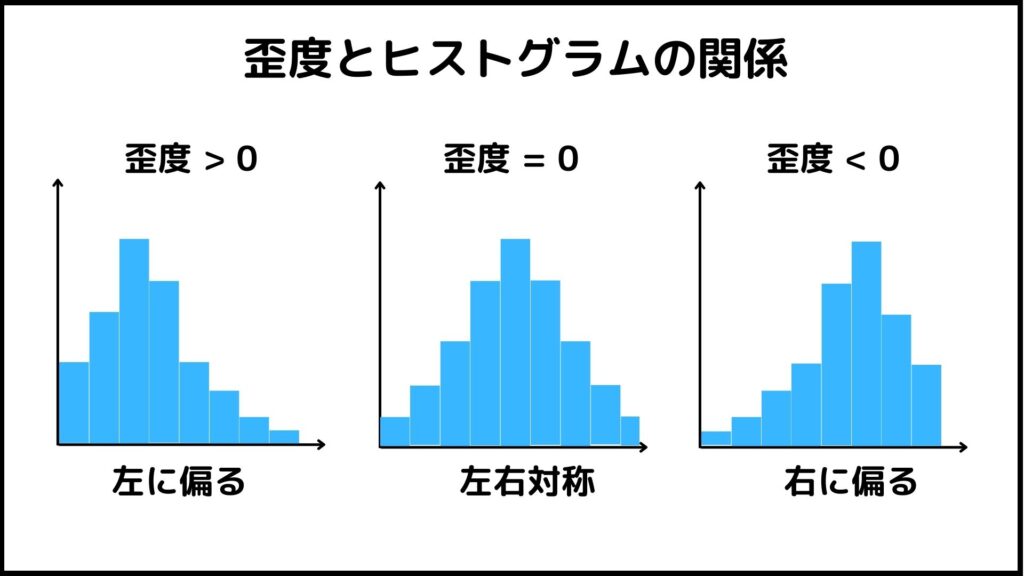
歪度が0のときは左右対称のヒストグラムになります。正規分布の歪度は0になります。歪度は0を基準にしてどちらにデータが偏っているかを数値で表します。
歪度が0より大きいときヒストグラムは左に偏ります。(右に長い裾を持つとも言います。)
歪度が0より小さいときヒストグラムは右に偏ります。(左に長い裾を持つとも言います。)
歪度は3次の中心モーメントを標準偏差の3乗で割り算して求めます。気になる人は調べてみてください!
尖度とは
尖度はヒストグラム(データの分布)がどれだけ尖っているかを表す指標です。
・尖度が大きいとき : 尖っている
・尖度が小さいとき : 平らになる
※正規分布の尖度は3になります!
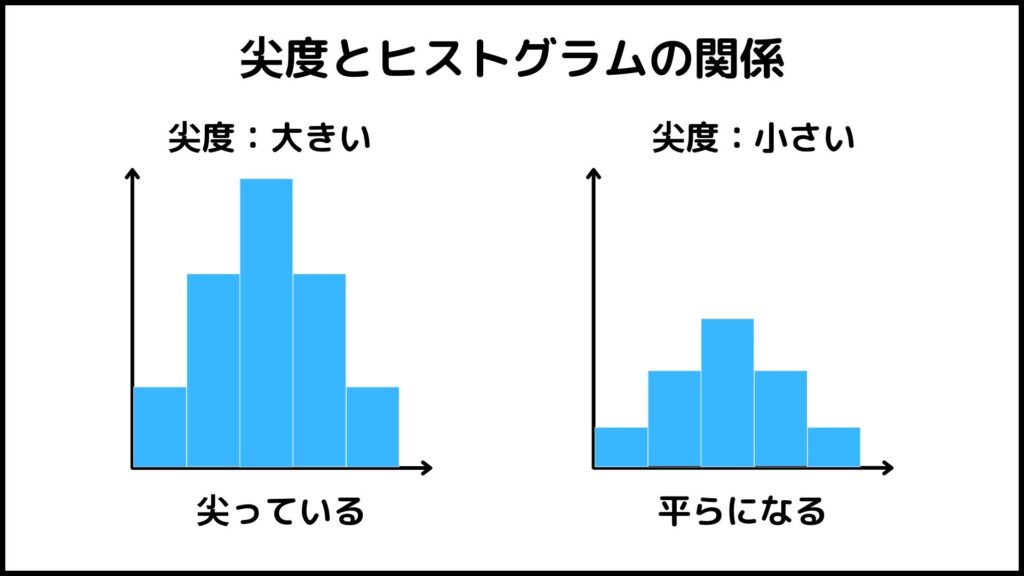
尖度が大きいときヒストグラムは尖り、歪度が小さいときヒストグラムは平らになります。
尖度は4次の中心モーメントを標準偏差の4乗で割り算して求めます。また正規分布の尖度は3になるので、上記の計算式から3を引いたものを尖度と定義する場合もあります。気になる人はぜひ調べてみてください!
ここまで歪度と尖度の説明をしてきましたが、ここからは実際にNBAのデータを使って歪度と尖度を計算していきましょう!
NBAのデータを使って歪度と尖度を求める
それではやってみましょう。今回も前回と同じようにNBA REFERENCEで取得した21-22シーズンのスタッツを使いたいと思います。
データはここから:Basketball Statistics & History of Every Team & NBA and WNBA Players | Basketball-Reference.com
今まで通りgoogle colabからpandasを使って歪度を求めたいと思います。データの前処理や事前準備は第1回の記事で解説しているのでそちらも読んでみてください。データはdfとして読み込んでいます。
#データの表示(先頭だけ)
df.head()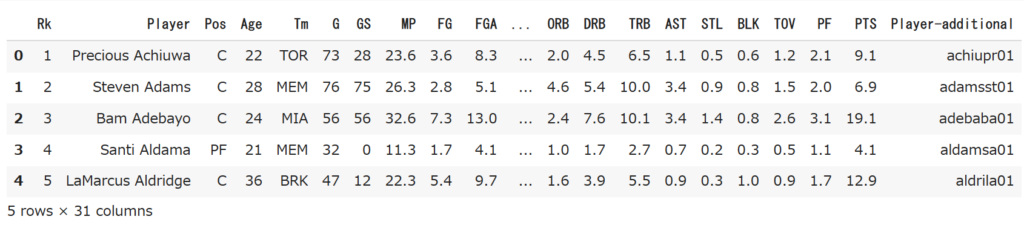
データはこんな感じです。今回は平均得点数(PTS)についてそれぞれ歪度と尖度を求めていこうと思います。それではいってみましょう!
# numpy.ndarray型に変換
PTS = np.array(df["PTS"])
# グラフ作成とグラフの大きさを宣言
fig = plt.figure(figsize=(15,12))
# PTSのグラフを作る
ax = fig.add_subplot(3,1,1)
Dosuu=ax.hist(PTS, bins=14, range = (0, 35), color = "darksalmon") #ヒストグラムを作る
ax.set_xlabel("平均得点数") # x軸のラベルを付ける
ax.set_ylabel("人数") # y軸のラベルを付ける
ax.set_title("平均得点数のヒストグラム") # タイトルをつける
ax.set_xticks(np.linspace(0,35,14+1)) # x軸の目盛りを付ける
ax.set_yticks(np.arange(0,120+1, 20)) # y軸の目盛りを付ける
# グラフの表示
plt.show()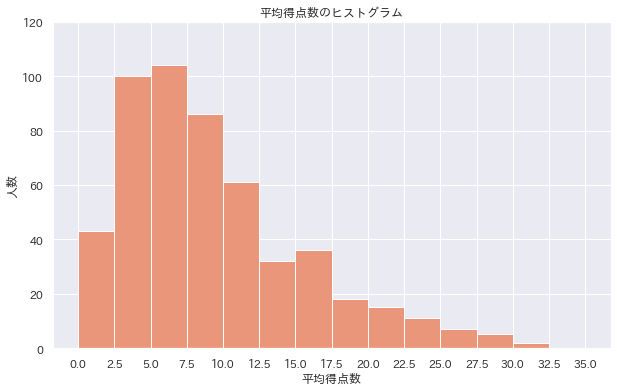
平均得点数のヒストグラムは上図のようになっています。左に偏っているので歪度は正の値を取っていそうですね。実際に計算してみましょう。歪度は.skew()で計算できます。
# 歪度を計算
df["PTS"].skew()
ということでやはり0より大きい値を取っていましたね。
次に尖度について求めてみましょう。尖度は.kurt()でで計算できます。
# 尖度を計算
df["PTS"].kurt()
恐らくpandasでの尖度は正規分布が0として定義されているので、この値は正規分布より尖っていると言えますね。
おわりに
いかがでしたか。
今回の記事では歪度と尖度について実際のデータを用いて説明していきました。データの偏りや尖りが数値化できるのは非常に興味深いですよね。
これからもこのようなデータ分析について話していこうと思います。ぼくが一番勉強になるので続けていきたいです!
最後までこの記事を読んでくれてありがとうございました。
この記事が役に立ったら幸いです。




