【最適解を求めるのは諦める】CBCソルバーの最適性ギャップの条件をいじって短時間でまあまあ良い解が得られないか試してみた

この記事のキーワード

整数計画問題をソルバーで解くと時間がかかる…
短時間でまあまあ良い解が欲しいな…
ソルバーによる計算結果のログが見たい…

はじめに

こんにちは！しゅんです！

最近ある問題をソルバーで解いてたときにこう思いました。

別に最適解を求める必要はないから、短時間である程度良い解を求めたいな～

特に実務で最適化問題を扱うときはこう考える場合が多いんじゃないでしょうか。ということでこの記事では、ソルバーの最適性ギャップの設定をいじってこの問題に対処できないか実験してみたいと思います。

それではやっていきましょう！

普段は組合せ最適化の記事を書いてたりします。
ぜひ他の記事も読んでみてください！

もっとみる

このブログの簡単な紹介はこちらに書いてあります。
興味があったら見てみてください。

このブログについて

このブログでは経営工学を勉強している現役理系大学生が、経営工学に関することを色々話していきます！

ぼくが経営工学を勉強している中で感じたことや、興味深かったことを皆さんと共有出来たら良いなと思っています。

そもそも経営工学とは何なのでしょうか。Wikipediaによると

経営工学（けいえいこうがく、英: engineering management）は、人・材料・装置・情報・エネルギーを総合したシステムの設計・改善・確立に関する活動である。そのシステムから得られる結果を明示し、予測し、評価するために、工学的な分析・設計の原理・方法とともに、数学、物理および社会科学の専門知識と経験を利用する。

引用元 : 経営工学 – Wikipedia

長々と書いてありますが、要は経営、経済の課題を理系的な観点から解決する学問です。

今回扱う問題（巡回セールスマン問題）

今回は巡回セールスマン問題（Traveling Salesman Problem）を解いてみようと思います。この記事でも簡単に説明はしますが、詳細な説明は過去の記事で行っているのでぜひそちらを見てみてください。

2024年1月27日【これでわかる！】MTZ制約を使って巡回セールスマン問題を整数計画問題として定式化してpythonで解いてみた

巡回セールスマン問題ってなに？

巡回セールスマン問題とはいくつかの地点が与えられたときに、全ての地点を丁度1回だけ訪れてまた戻って来る経路の中で、一番最適な経路は何かを考えます。

よくあるのは移動距離が最も小さくなるような経路を見つけることです。巡回セールスマン問題はNP困難であることが知られています。

巡回セールスマン問題を混合整数計画問題として定式化する

パラメータ：
\(V\) : 都市の集合
\(d_{ij}\) : 地点\(i\)と地点\(j\)間の距離

変数：

\(x_{ij} \in \{0,1\}\) : 地点\(i\)から地点\(j\)に向かうなら1、そうでないなら0を取る0-1変数
\(y_{i}\) : MTZ制約で用いる連続変数

定式化：
\( \min \;\;\; \sum\limits_{i \in V}\sum\limits_{j \in V , i \ne j} d_{ij}x_{ij}\)
\(\;\text{s.t.}\;\;\;\sum\limits_{j \in V, i \ne j}x_{ij} = 1 \;\;\; (\forall i \in V)\)
\(\;\;\;\;\;\;\;\;\; \sum\limits_{i \in V, i \ne j}x_{ij} = 1 \;\;\; (\forall j \in V)\)
\(\;\;\;\;\;\;\;\;\; y_{i}-y_{j}+|V|x_{ij} \leq |V|-1\)
　　　　　　\((\forall i \in V/\{0\}, \; \forall j \in V/\{0\}, \; i \ne j)\)
\(\;\;\;\;\;\;\;\;\; x_{ij} \in \{0,1\} \;\;\; (\forall i \in V, \forall j \in V, i \ne j)\)

MIPで定式化してみました。今回はMTZ制約を使ってみました。定式化の方法やMTZ制約の説明は過去の記事で解説しています。

2024年1月27日【これでわかる！】MTZ制約を使って巡回セールスマン問題を整数計画問題として定式化してpythonで解いてみた

巡回セールスマン問題をpythonで解いてみる

まず問題例を生成します。\([0,100] \times [0,100]\)の2次元座標上からランダムに点を選びます。

2地点間の距離はユークリッド距離で定義しています。地点数は50個にしてみました。

import numpy as np
import pandas as pd
import matplotlib.pyplot as plt

def generate_tsp_data(num_vertices, seed=42):
    np.random.seed(seed)
    
    # 2次元座標をランダムに生成（0〜100の範囲）
    coordinates = {i: (np.random.uniform(0, 100), np.random.uniform(0, 100)) for i in range(num_vertices)}
    
    # ユークリッド距離を計算
    distances = {
        (i, j): np.sqrt((coordinates[i][0] - coordinates[j][0])**2 + (coordinates[i][1] - coordinates[j][1])**2)
        for i in range(num_vertices) for j in range(num_vertices) if i != j
    }
    
    return coordinates, distances

# 頂点数を指定
num_vertices = 50
V = [i for i in range(num_vertices)]
V_0 = V[1:]
# TSPデータを生成
coordinates, d = generate_tsp_data(num_vertices)

上図を表示するコード

plt.figure(figsize=(8, 6))

# 都市のプロット
for i, (x, y) in coordinates.items():
    plt.scatter(x, y, color="blue", s=100, zorder=2)
    plt.text(x + 1, y + 1, str(i), fontsize=12, color="black")

plt.xlabel("X Coordinate")
plt.ylabel("Y Coordinate")
plt.title("Optimal TSP Route")
plt.grid(True)
plt.show()

上図のような問題例が生成されました。それでは次にpulpを使って問題を定式化しましょう。ソルバーはCBCに設定します。計算時間の制限を1800秒に制限しました。

import pulp

# 整数計画問題の定式化
prob = pulp.LpProblem(sense=pulp.LpMinimize)
x = pulp.LpVariable.dicts("x", [(i, j) for i in V for j in V if i != j], cat="Binary")
y = pulp.LpVariable.dicts("y", V_0, cat="Continuous")

# 目的関数
prob += pulp.lpSum(d[(i, j)] * x[i, j] for i in V for j in V if i != j)

# 各都市を1度だけ訪れる
for i in V:
    prob += pulp.lpSum(x[i, j] for j in V if i != j) == 1

for j in V:
    prob += pulp.lpSum(x[i, j] for i in V if i != j) == 1

# サブツアー制約（MTZ制約）
for i in V_0:
    for j in V_0:
        if i != j:
            prob += y[i] - y[j] + len(V) * x[i, j] <= len(V) - 1

# CBCソルバーの設定
solver = pulp.PULP_CBC_CMD(
    timeLimit=1800,
    msg=True
)

# 最適化実行
result = prob.solve(solver)

最適解が得られたので図示してみます。

上図を表示するコード

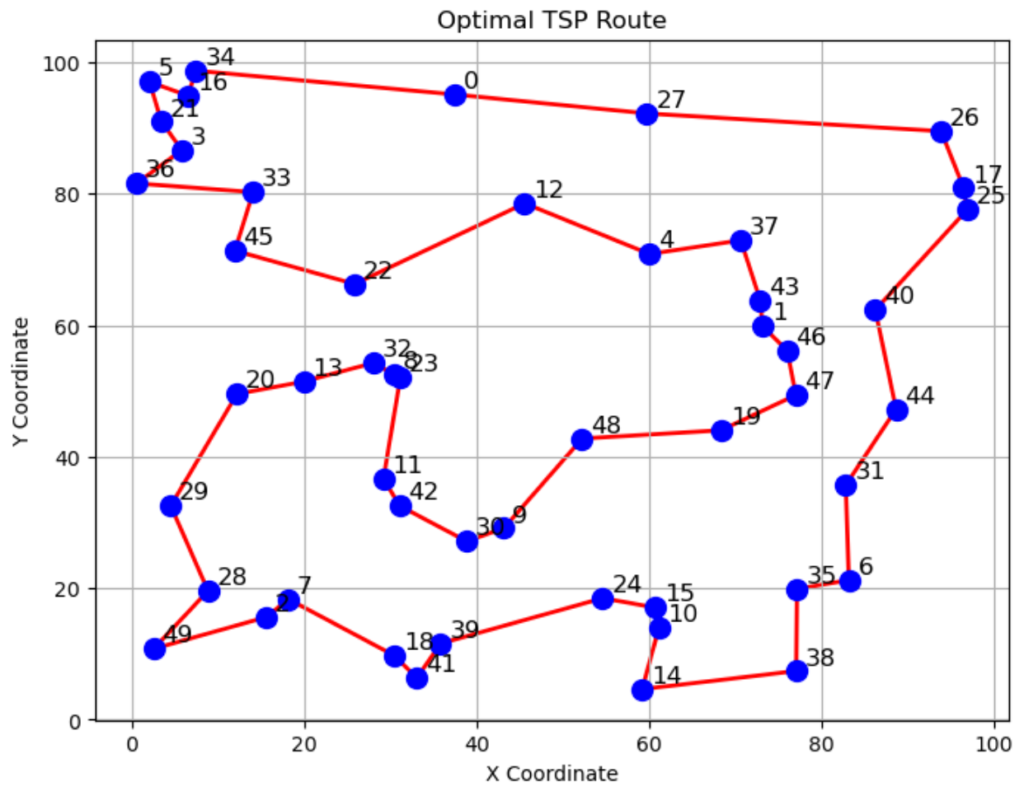
import matplotlib.pyplot as plt

# 1. 最適解の取得
route_edges = [(i, j) for i in V for j in V if i != j and pulp.value(x[i, j]) == 1]

# 2. ルートの構成
route_dict = {i: j for i, j in route_edges}  # i -> j のマッピング
start = 0  # 出発点（仮に0とする）
optimal_route = [start]

while len(optimal_route) < len(V):
    next_city = route_dict[optimal_route[-1]]
    optimal_route.append(next_city)

# 3. 可視化
plt.figure(figsize=(8, 6))

# 都市のプロット
for i, (x, y) in coordinates.items():
    plt.scatter(x, y, color="blue", s=100, zorder=2)
    plt.text(x + 1, y + 1, str(i), fontsize=12, color="black")

# ルートのプロット
for k in range(len(optimal_route) - 1):
    i, j = optimal_route[k], optimal_route[k + 1]
    x_vals = [coordinates[i][0], coordinates[j][0]]
    y_vals = [coordinates[i][1], coordinates[j][1]]
    plt.plot(x_vals, y_vals, color="red", linestyle="-", linewidth=2, zorder=1)

# 始点から終点へ戻る線を引く
i, j = optimal_route[-1], optimal_route[0]
plt.plot([coordinates[i][0], coordinates[j][0]], 
         [coordinates[i][1], coordinates[j][1]], color="red", linestyle="-", linewidth=2, zorder=1)

plt.xlabel("X Coordinate")
plt.ylabel("Y Coordinate")
plt.title("Optimal TSP Route")
plt.grid(True)
plt.show()

ソルバーのログを見てみる

Result - Optimal solution found

Objective value:                559.86465601
Enumerated nodes:               18812
Total iterations:               1403801
Time (CPU seconds):             829.20
Time (Wallclock seconds):       829.20

Option for printingOptions changed from normal to all
Total time (CPU seconds):       829.30   (Wallclock seconds):       829.30

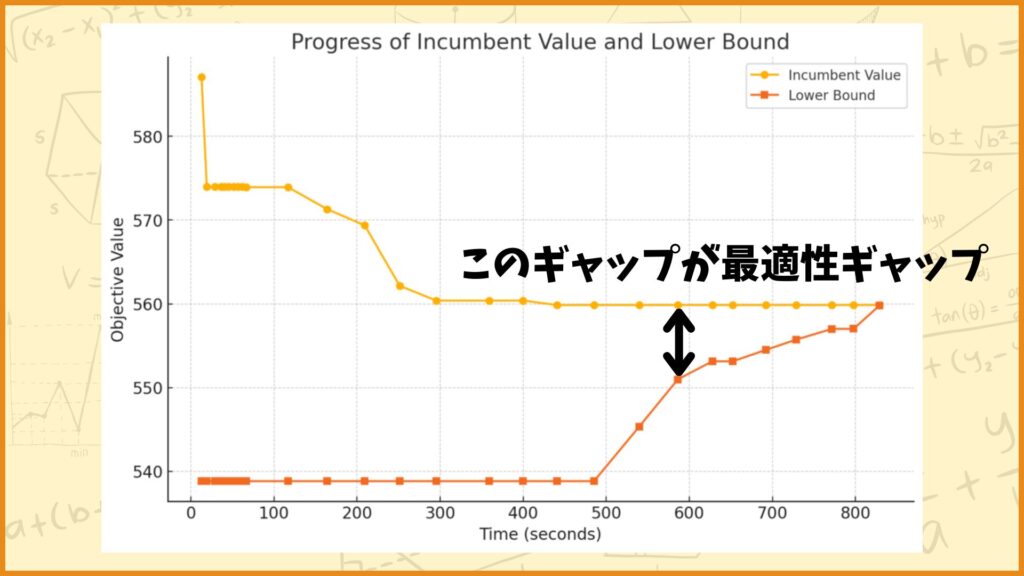
ソルバーのログを見ると約829秒（14分くらい）で最適解が得られていることが分かります。また時間ごとの暫定値と下界は下図のようになっていました。

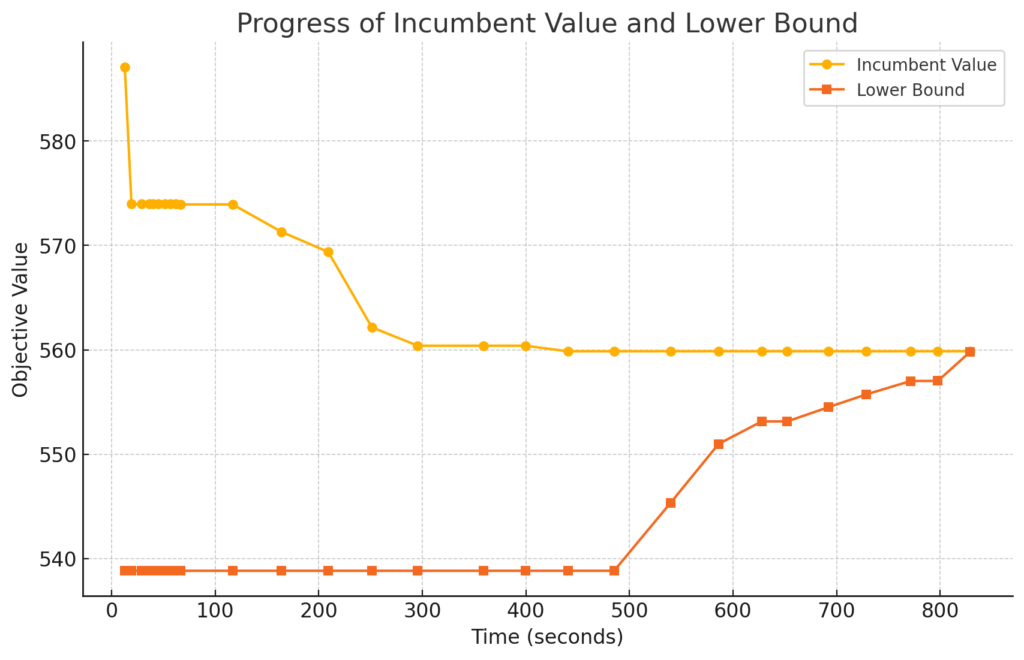
Incumbent Value：暫定解の目的関数値（これ以上最適値は大きくならない）
Lower Bound：下界（これ以上最適値は小さくならない）

これを見ると割と早い段階で最適解を見つけていて、最適性の証明に時間がかかっているようです。

ソルバーの最適性ギャップの設定をいじってみる

もっと早めに最適解が得られないかな～と思って考えついたのが、

最適性ギャップの終了条件をもっと緩めれば良いんじゃね？

ということでした。

CBCソルバーの引数で「gapRel」というものがあり、これは最適性ギャップがいくつになったら計算を終了するかを設定できるものです。下の設定では最適性ギャップが2%になる時点で計算が終了するようにしています。

import pulp

# 整数計画問題の定式化
prob = pulp.LpProblem(sense=pulp.LpMinimize)
x = pulp.LpVariable.dicts("x", [(i, j) for i in V for j in V if i != j], cat="Binary")
y = pulp.LpVariable.dicts("y", V_0, cat="Continuous")

# 目的関数
prob += pulp.lpSum(d[(i, j)] * x[i, j] for i in V for j in V if i != j)

# 各都市を1度だけ訪れる
for i in V:
    prob += pulp.lpSum(x[i, j] for j in V if i != j) == 1

for j in V:
    prob += pulp.lpSum(x[i, j] for i in V if i != j) == 1

# サブツアー制約（MTZ制約）
for i in V_0:
    for j in V_0:
        if i != j:
            prob += y[i] - y[j] + len(V) * x[i, j] <= len(V) - 1

# CBCソルバーの設定
solver = pulp.PULP_CBC_CMD(
    timeLimit=1800,
    gapRel=0.02, # 最適性ギャップが2%になったら計算を終了する。
    msg=True
)

# 最適化実行
result = prob.solve(solver)

ということで下記の結果が得られました。「Objective value」と「Lower bound」を見ると、少し差がありますが2%以内のギャップなので計算が終了しています。

Result - Optimal solution found (within gap tolerance)

Objective value:                559.86465601
Lower bound:                    549.021
Gap:                            0.02
Enumerated nodes:               11401
Total iterations:               870351
Time (CPU seconds):             542.22
Time (Wallclock seconds):       542.22

計算時間は約542秒（9分くらい）と先ほどよりも計算時間は短くなっています。ちなみにIncumbent Valueは400秒くらいで最適値に到達しているので、ここで計算を打ち切っても最適解が得られています。

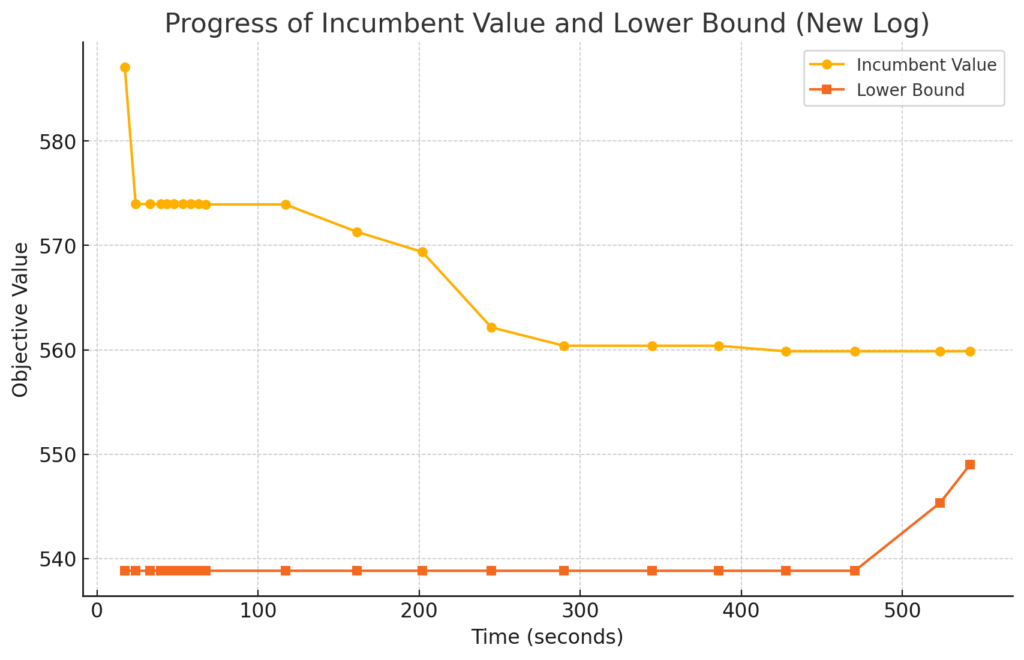
ということで今回の問題では計算時間を短縮することができました。しかしこの手法が実用的かと言えば微妙なのかなとも思いました。

最適化ギャップを緩めても意味なかった例

今度は地点数を80地点にしてみました。timelimitを1800秒（30分）に設定したのでそこで計算が終了しています。ログを見ると、ギャップが35%あります。

Result - Stopped on time limit

Objective value:                850.27322012
Lower bound:                    630.857
Gap:                            0.35
Enumerated nodes:               13783
Total iterations:               1113972
Time (CPU seconds):             1801.09
Time (Wallclock seconds):       1801.09

Incumbent ValueとLower Boundの推移は下図の通りです。こういう問題だと最適性ギャップを2%にしても意味がなかったです。

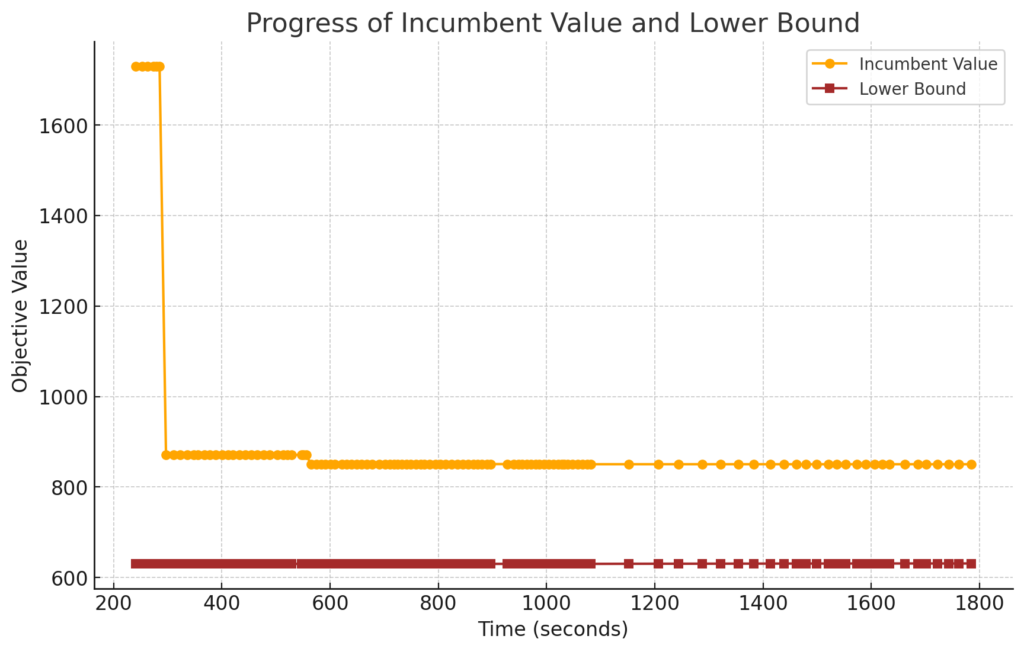
そもそも実用的なことを考えると、「最適値とのギャップが2%以内になるようにしたい」って要望はほとんどなく、むしろ「計算時間を30分以内に収めたい」という時間に対する要望がほとんどなんじゃないかなと思いました。

そうなったら最適性ギャップの設定をするんじゃなくてtimelimitの設定をした方が良いのかなと思いました。