- トポロジカルソートってなに?
- トポロジカルソートって何のためにやるの?
- トポロジカルソートをpythonで実装したい…
こんにちは!しゅんです!
トポロジカルソートはグラフ理論で登場する用語で、各要素の依存関係を分かりやすく表すことができます。
この記事ではトポロジカルソートというアルゴリズムについて、基本的な考え方やpythonでの実装方法を分かりやすく解説していきます。
それでは解説していきましょう!
普段は組合せ最適化の記事を書いてたりします。
ぜひ他の記事も読んでみてください!
このブログの簡単な紹介はこちらに書いてあります。
興味があったら見てみてください。
このブログでは経営工学を勉強している現役理系大学生が、経営工学に関することを色々話していきます!
ぼくが経営工学を勉強している中で感じたことや、興味深かったことを皆さんと共有出来たら良いなと思っています。
そもそも経営工学とは何なのでしょうか。Wikipediaによると
経営工学(けいえいこうがく、英: engineering management)は、人・材料・装置・情報・エネルギーを総合したシステムの設計・改善・確立に関する活動である。そのシステムから得られる結果を明示し、予測し、評価するために、工学的な分析・設計の原理・方法とともに、数学、物理および社会科学の専門知識と経験を利用する。
引用元 : 経営工学 – Wikipedia
長々と書いてありますが、要は経営、経済の課題を理系的な観点から解決する学問です。
トポロジカルソートの基本的な考え方
トポロジカルソート:
辺の向きが一方向になるように頂点を並べ替えること。
下にあるグラフを使って考えてみましょう。
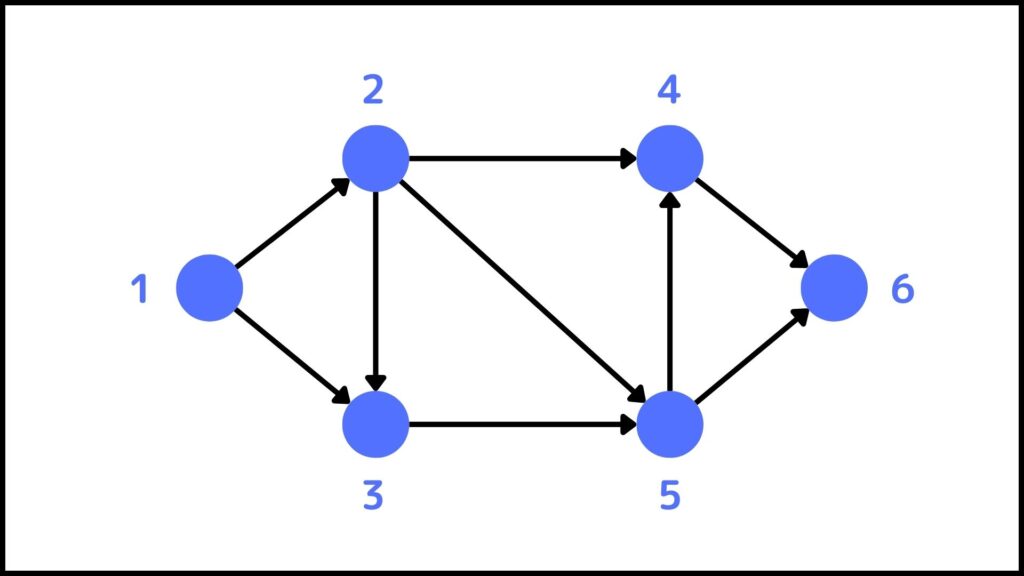
トポロジカルソートで気にするのは辺の向きです。この辺の向きが一方向になるように並べ替えることをトポロジカルソートと言います。
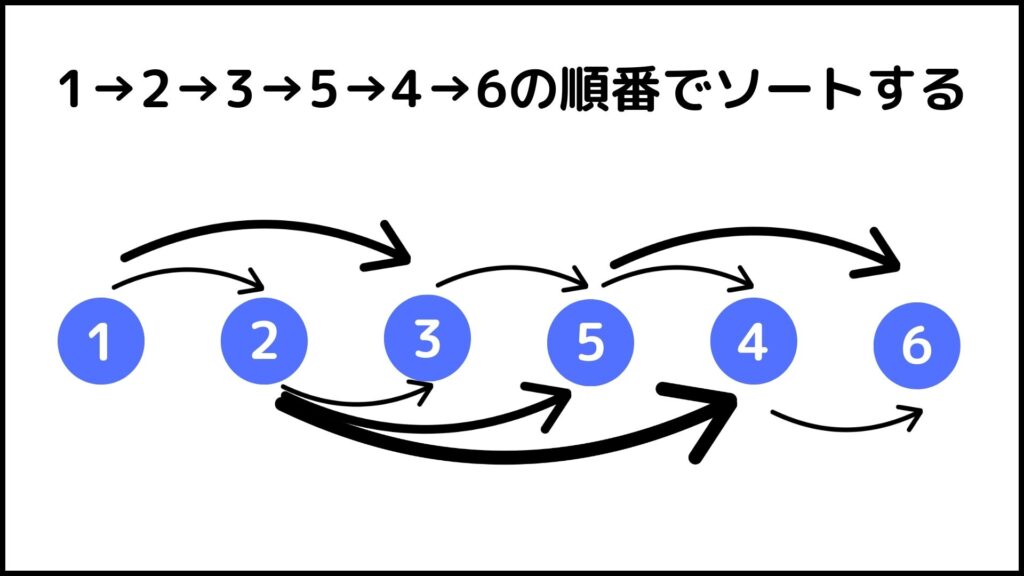
1→2→3→5→4→6の順番で並べ替えてみました。(矢印の太さは関係ないです。)
これを見ると
辺の向きが全部左から右に向かっている
ことが分かります。このように頂点を並び替えることをトポロジカルソートと言います。
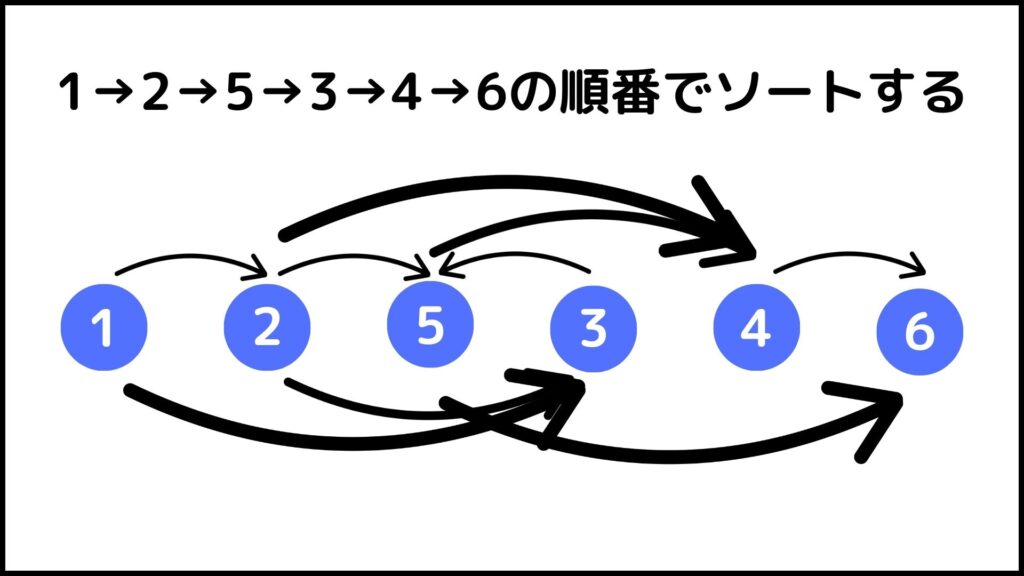
1→2→5→3→4→6の順番で並べ替えました。これを見ると
5と3の間だけ右方向に辺が向かっている
ことが分かります。向きが違う辺があるので上の並べ方はトポロジカルソートの並び方ではありません。
トポロジカルソートは有向非巡回グラフ(DAG)で使える
トポロジカルソートは特定の条件を満たすグラフに対して適用することができるソートです。その条件とは
トポロジカルソートが使えるグラフの条件:
有向非巡回グラフ(Directed Acyclic Graph)であること
です。この条件について詳しく見ていきましょう。
有向グラフであること
1つ目の条件は有向グラフであることです。これは直観的にも分かりやすいと思います。
要は頂点同士を結ぶ辺に方向がなきゃだめだということです。
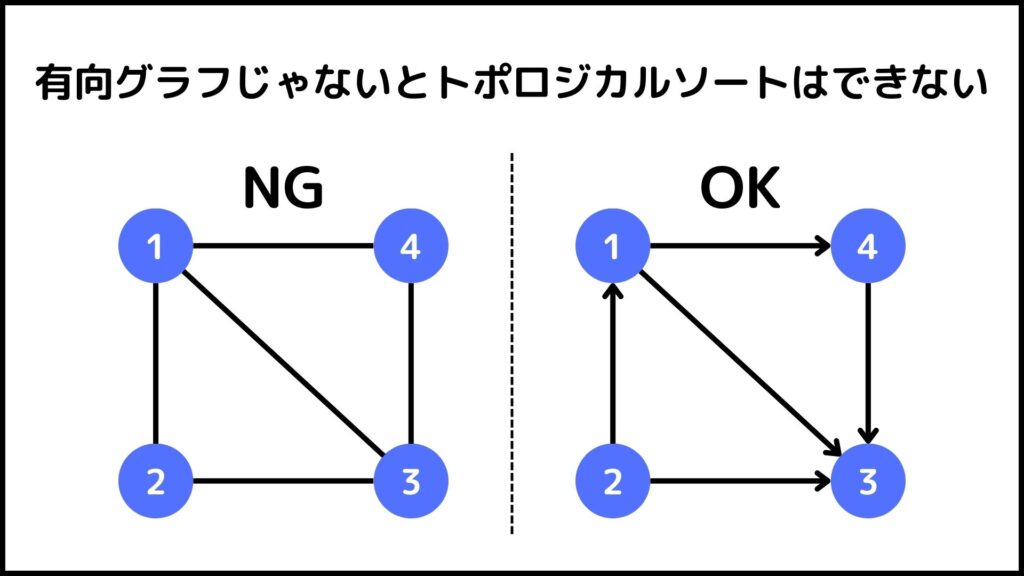
非巡回グラフであること
2つ目の条件は非巡回グラフであることです。非巡回グラフとは
閉路がないグラフ
のことです。

上のグラフのNG例を見ると
1→4→3→2→1
の閉路があることが分かります。このようにグラフ中に閉路がある巡回グラフではトポロジカルソートを使うことができません。
有向非巡回グラフのことをDAG(Directed Acyclic Graph)といいます。
トポロジカルソートって何のためにやるの?
トポロジカルソートの目的:
グラフ中の頂点間の依存関係を明らかにすること
トポロジカルソートの目的はグラフ中における頂点同士の依存関係を明らかにすることです。

例えば上図を見ると頂点1からは頂点2と頂点3に矢印が伸びていますね。これは
「頂点1が先に処理されてから頂点2、頂点3が処理される」
と言うことを表します。
他にも例えば「洗濯」をグラフ理論を用いて分析する場合を考えてみましょう。
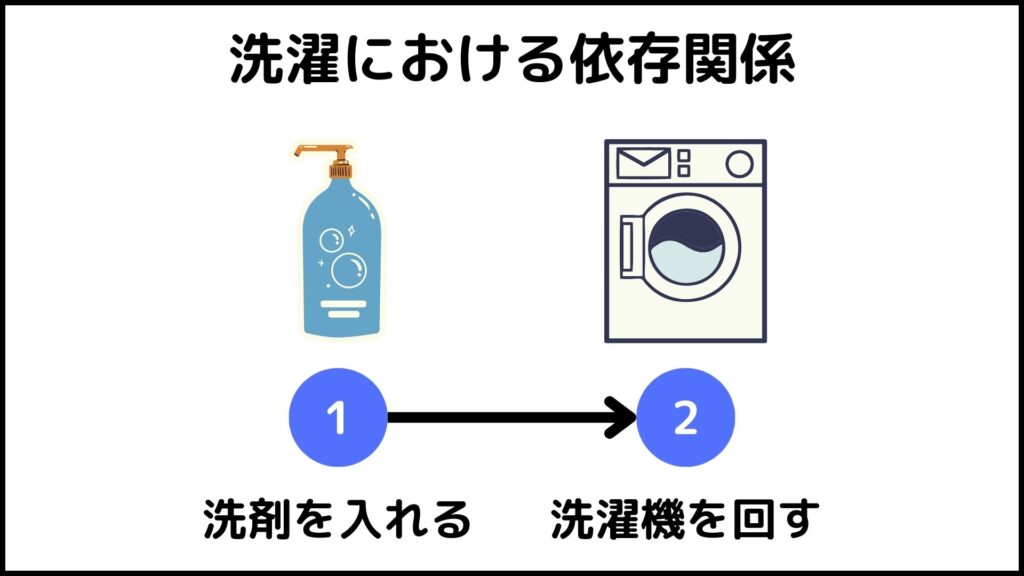
上図のように
頂点1:洗剤を入れる
頂点2:洗濯機を回す
という作業をそれぞれ表し、辺の向きが行動の依存関係を表すと考えると、頂点1から頂点2に矢印が伸びるはずです。なぜなら選択をするときは必ず「洗剤を入れる」という作業を行ってから「洗濯機を回す」という作業を行うためです。
このように複数の作業がある場合に、それらの依存関係を明らかにして分析しやすくするのがトポロジカルソートの目的です。
味噌汁を作る手順をトポロジカルソートしてみる
ここで一つ日常の例を使ってトポロジカルソートを解説していきます。今回は「味噌汁を作る」ことに対してグラフを作ってトポロジカルソートをやっていこうと思います。
まず初めに味噌汁を作る手順を以下のように決めたいと思います。
- 鍋に水を入れて火にかける
- 油揚げを切る
- 豆腐を切る
- キノコを切る
- 鍋に具材を入れる
- だし汁を入れる
- 味噌汁を溶く
※具材は豆腐を一番最初に切る
※だし汁の後に味噌汁を入れる
頂点の番号も上のようにしてグラフを作っていきます。グラフは以下のようになります。
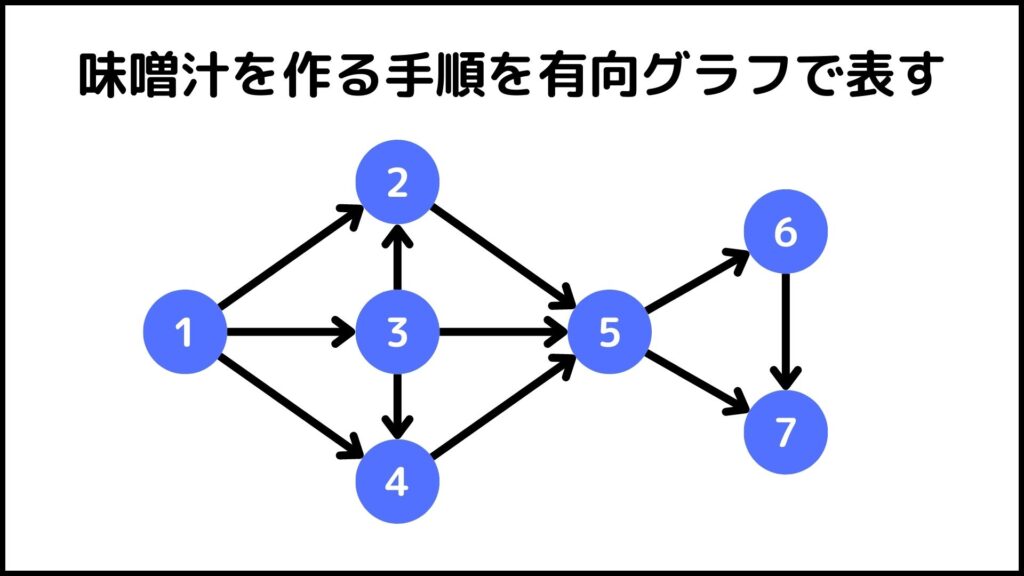
これをトポロジカルソートすると以下のようになります。

トポロジカルソートを適用すると1→3→2→4→5→6→7という順番になります。(2と4の位置を入れ替えてもOKです。)例えば3,2,4は5に矢印が伸びていますが、これは
3,2,4の処理が実行されないと5の処理を実行することができない
ということを表しています。
2,3,4は各具材を切る処理で5は鍋に具材を入れる処理なので、つまり具材を切ってからじゃないと鍋に入れることができないということを表しています。
ぶっちゃけ味噌汁を作るというような簡単な手順ではトポロジカルソートがどうすごいのかが伝わりにくいですが、例えば銀行のシステムや企業の大規模プロジェクトといった手順が非常に複雑なシステムを分析する場合には非常に有用です。

pythonでトポロジカルソートを実装する
最後にpythonでトポロジカルソートを実装してみたいと思います。以下がコードの例です。
def topological_sort(graph):
# 初期化
in_degree = {node: 0 for node in graph} # 各ノードの入次数を初期化
queue = [] # 入次数が0のノードを保持するキュー
for node in graph:
for neighbor in graph[node]:
in_degree[neighbor] += 1 # 各ノードの入次数を計算
for node in graph:
if in_degree[node] == 0:
queue.append(node) # 入次数が0のノードをキューに追加
# トポロジカルソートの実行
result = []
while queue:
node = queue.pop(0)
result.append(node) # ソートされた結果にノードを追加
for neighbor in graph[node]:
in_degree[neighbor] -= 1 # 入次数を減らす
if in_degree[neighbor] == 0:
queue.append(neighbor) # 入次数が0になったらキューに追加
# グラフにサイクルがある場合は例外を発生させる
if len(result) != len(graph):
raise ValueError("Graph contains at least one cycle")
return resultこのコードは隣接リストが入力されたときに非巡回グラフだったらトポロジカルソートされた頂点リストを返し、閉路(サイクル)がある場合はエラーを返す関数です。
隣接リストとは、ある頂点と隣接してる頂点を格納しているリストです。例えば頂点1から出ている矢印が頂点2,頂点3に繋がっているときは1:[2,3]と表します。
このプログラムを使って下の複雑なグラフをトポロジカルソートしてみましょう。
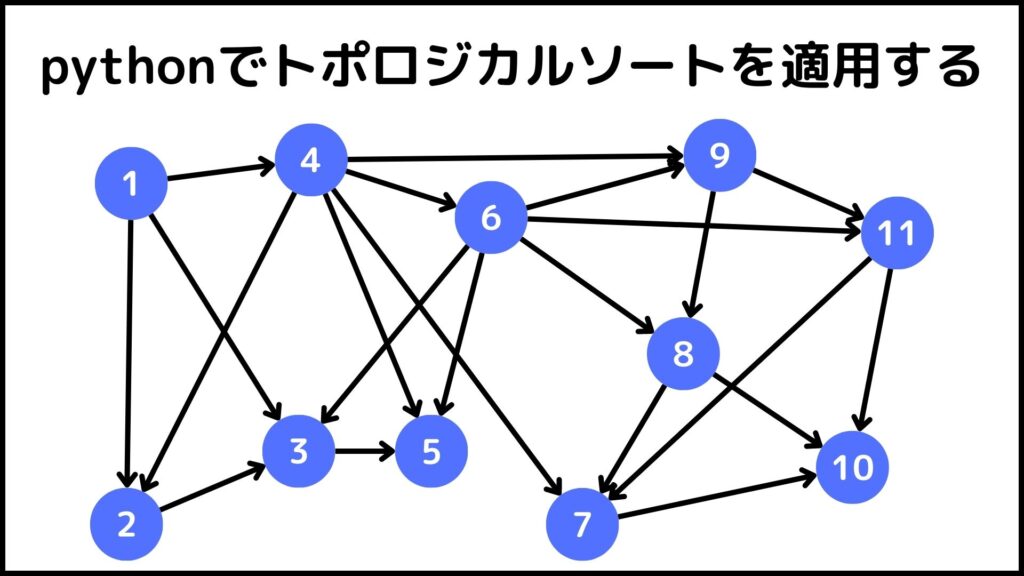
このグラフを隣接リストで表すと以下のようになります。
graph = {
1:[2,3,4],
2:[3],
3:[5],
4:[2,5,6,9],
5:[],
6:[3,5,8,9,11],
7:[10],
8:[7,10],
9:[8,11],
10:[],
11:[10]
}例えば1の所を見ると2,3,4が格納されていますが、これは頂点1からは頂点2,頂点3,頂点4に繋がっていると言うことを表しています。それではトポロジカルソートを実行してみましょう。
topological_sort(graph)
ということでトポロジカルソートを実行することができました。このように複雑なグラフになってもプログラミングをすればトポロジカルソートを実行することができます。
おわりに
いかがでしたか。
今回の記事ではトポロジカルソートについて解説していきました。
今後もこのような経営工学に関する記事を書いていきます!
最後までこの記事を読んでくれてありがとうございました。






