- 巡回セールスマン問題ってなに?
- 巡回セールスマン問題を整数計画問題として定式化したい…
- 巡回セールスマン問題をpythonで解きたい…
こんにちは!しゅんです!
この記事では具体例を使って巡回セールスマン問題を解説したいと思います!
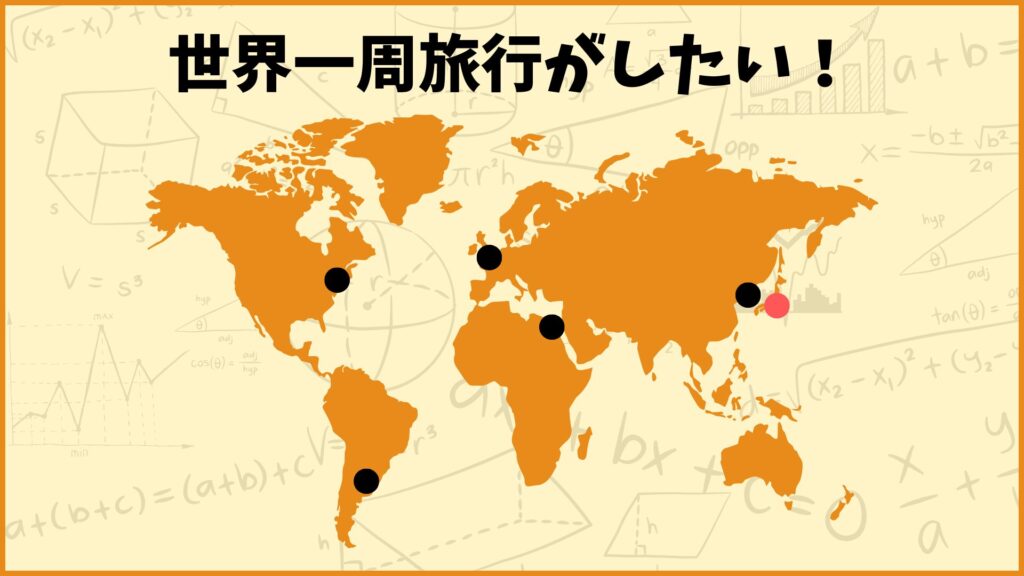
今回は世界一周旅行を例に挙げて巡回セールスマン問題について考えていきます。日本から出発して合計5つの国を旅行してまた日本に帰ってくるルートを求めたいと思います。
それではやっていきましょう!
組合せ最適化の記事を書いてたりします。
ぜひ他の記事も読んでみてください!
このブログの簡単な紹介はこちらに書いてあります。
興味があったら見てみてください。
このブログでは経営工学を勉強している現役理系大学生が、経営工学に関することを色々話していきます!
ぼくが経営工学を勉強している中で感じたことや、興味深かったことを皆さんと共有出来たら良いなと思っています。
そもそも経営工学とは何なのでしょうか。Wikipediaによると
経営工学(けいえいこうがく、英: engineering management)は、人・材料・装置・情報・エネルギーを総合したシステムの設計・改善・確立に関する活動である。そのシステムから得られる結果を明示し、予測し、評価するために、工学的な分析・設計の原理・方法とともに、数学、物理および社会科学の専門知識と経験を利用する。
引用元 : 経営工学 – Wikipedia
長々と書いてありますが、要は経営、経済の課題を理系的な観点から解決する学問です。
問題設定
それではまず最初に今回考えたい問題をちゃんと設定しましょう。
問題設定
・世界一周旅行を行う。
・東京から出発して合計5カ国を回ってまた日本に戻ってくる。
・旅行で行く都市は以下の通りである。
ニューヨーク(アメリカ)
ブエノスアイレス(アルゼンチン)
ソウル(韓国)
ロンドン(イギリス)
カイロ(エジプト)
目的
移動距離の合計が最小となるような旅行ルートを求めたい。
例えば以下のような旅行ルートがあります。
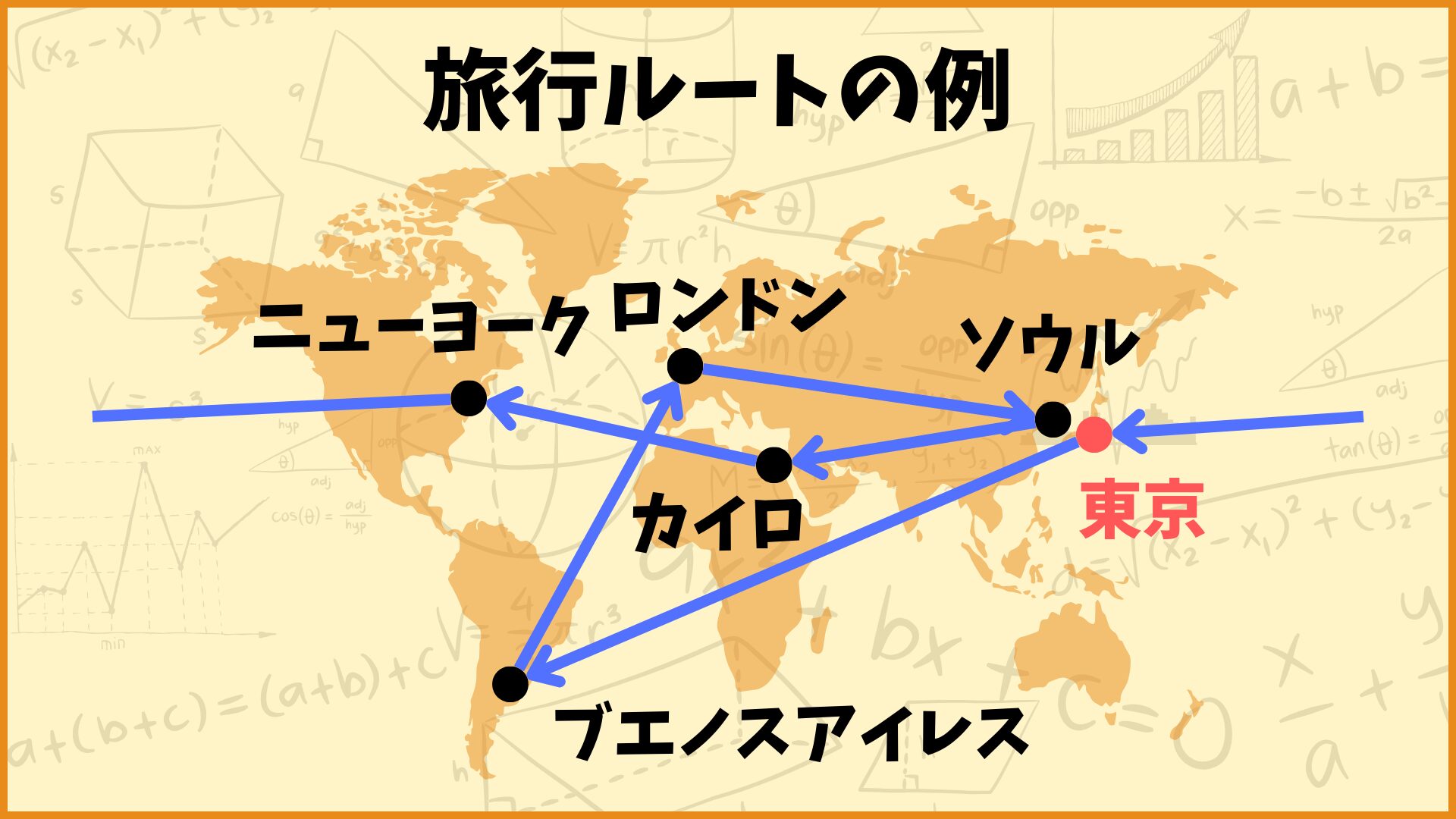
上図の例は
東京→ブエノスアイレス→ロンドン→ソウル→カイロ→ニューヨーク→東京
の旅行ルートです。目的関数は移動距離の合計とし、これが最小となるような旅行ルートを考えます。
現実の旅行ではおそらく他にも色々考えてルートを決めると思いますが、今回は単純に移動距離の合計の最小化を考えたいと思います。
整数計画問題として定式化
「記号の設定」、「目的関数の設定」、「制約条件の設定」の3つに分けて説明したいと思います。
記号の設定
パラメータとして都市の集合と各都市間の距離を設定します。変数は0-1変数\(x_{ij}\)を使いたいと思います。
パラメータ:
\(V = \{0,1,2,3,4,5\}\) : 都市の集合
\(d_{ij}\) : 都市\(i\)と都市\(j\)間の距離
変数:
\(x_{ij} \in \{0,1\}\) : 都市\(i\)から都市\(j\)に向かうなら1、そうでないなら0を取る0-1変数
各都市を数字で表しています。
0 : 東京
1 : ニューヨーク
2 : ブエノスアイレス
3 : ソウル
4 : ロンドン
5 : カイロ
各都市間の距離は以下のサイトを使って求めました。
2都市間の距離と方位角 – 高精度計算サイト (casio.jp)
目的関数の設定
この問題の目的は
「移動距離の合計が最小となるような旅行ルートを求めたい」
です。よって以下のように表すことができます。
目的関数:
\(\sum\limits_{i \in V}\sum\limits_{j \in V , i \ne j} d_{ij}x_{ij} \)
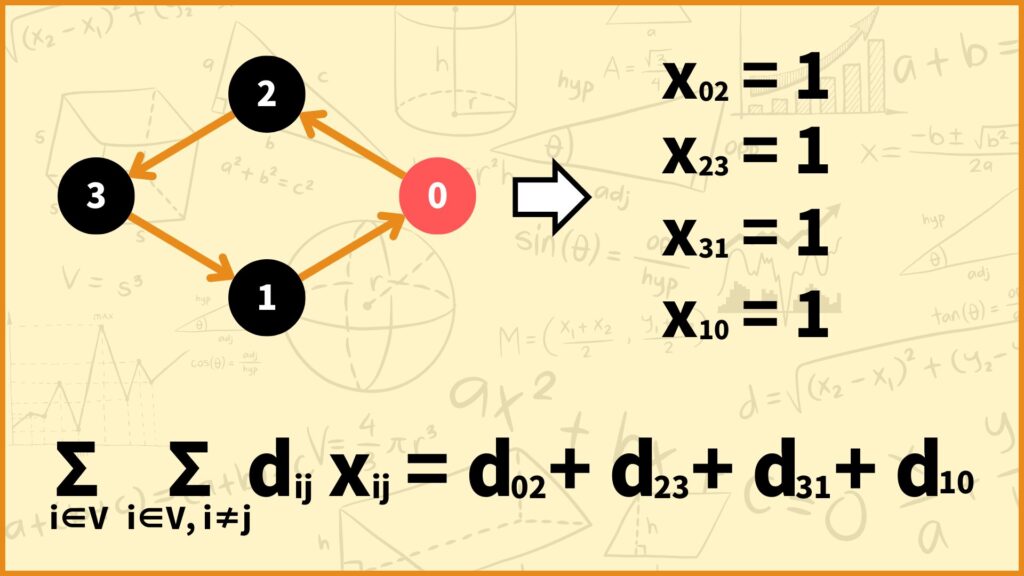
例えば\(V = \{0,1,2,3\}\)だとして0→2→3→1→0の順に回るとします。このとき変数の値は
\(x_{02} = x_{23} = x_{31} = x_{10} = 1\)
で他の変数の値は0となります。また目的関数値は
\(\sum\limits_{i \in V}\sum\limits_{j \in V , i \ne j} d_{ij}x_{ij}\)
\( = d_{02}x_{02} + d_{23}x_{23} + d_{31}x_{31} + d_{10}x_{10}\)
\( = d_{02}+d_{23}+d_{31}+d_{10}\)
となります。この値はこの旅行ルートの移動距離の合計と対応しています。回る都市の数\(|V|\)が変わっても同じように考えることができます。今回はこれを最小化します。
2つ目の\(\sum\)の所が\(i \ne j\)となっているのは自己ループを防ぐためです。仮に\(x_{22} = 1\)とすると都市2から都市2に向かうということになってしまいます。
この後の「pythonで解いてみる」の所でも説明しますが、そもそも変数を作る段階で\(x_{ii} \; (\forall i \in V)\)は作らないので\(i \ne j\)としないとエラーが出てしまいます。
今後登場する\(i \ne j\)はすべて同じ理由です。
\( \min \;\;\; \sum\limits_{i \in V}\sum\limits_{j \in V , i \ne j} d_{ij}x_{ij} \)
制約条件の設定
制約条件:
\(\sum\limits_{j \in V, i \ne j}x_{ij} = 1 \;\;\; (\forall i \in V)\) → ①
\(\sum\limits_{i \in V, i \ne j}x_{ij} = 1 \;\;\; (\forall j \in V)\) → ②
\(\sum\limits_{i \in S}\sum\limits_{j \in S, i \ne j}x_{ij} \leq |S| -1 \;\;\; (\forall S \subset V, |S| \geq 2)\) → ③
1つずつ解説していきます。
1つ目の制約
1つ目の制約:
\(\sum\limits_{j \in V, i \ne j}x_{ij} = 1 \;\;\; (\forall i \in V)\)
1つ目の制約は「全ての都市について、その都市から別の都市に向かう」ことを表しています。
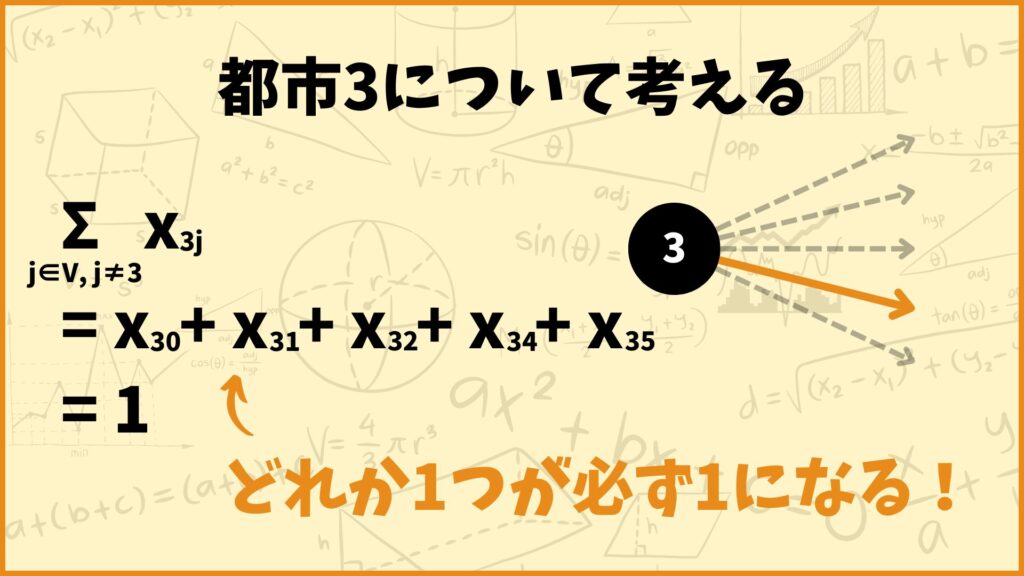
例えば都市3(ソウル)について考えてみましょう。制約式の左辺は
\(\sum\limits_{j \in V, j \ne 3}x_{3j}\)
\( = x_{30} + x_{31} + x_{32} + x_{34} + x_{35}\)
となります。変数\(x_{ij}\)は0か1しか取らないので、制約式が成り立つためには上記の5個の変数のうちどれか1つだけが1を取ることを表します。これは
「必ず都市3から他の都市に向かう」
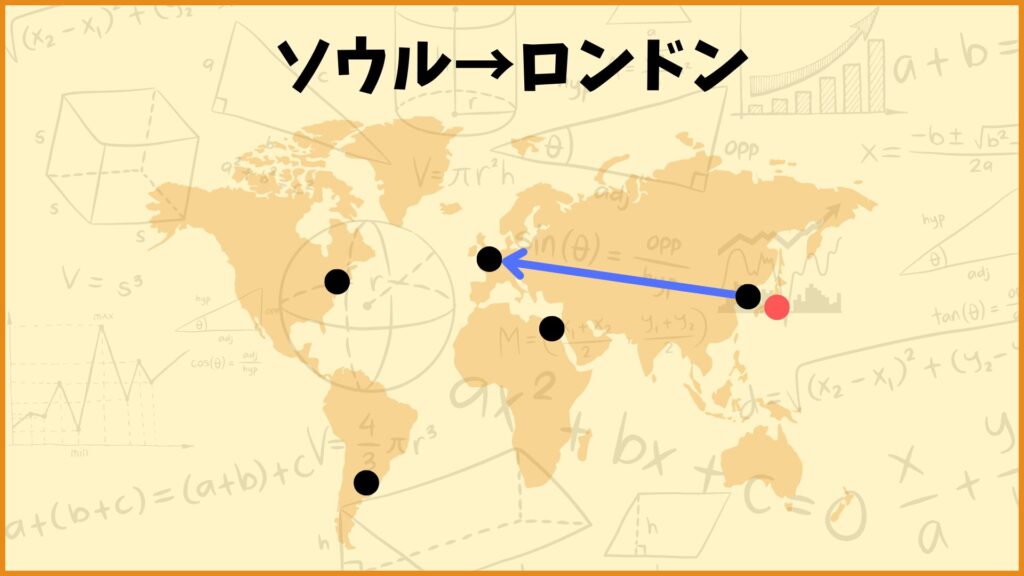
ということを表しています。例えば\(x_{34} = 1\)としましょう。これは
「都市3(ソウル)から都市4(ロンドン)に向かう」
ということを表しています。
2つ目の制約
2つ目の制約:
\(\sum\limits_{i \in V, i \ne j}x_{ij} = 1 \;\;\; (\forall j \in V)\)
2つ目の制約は「全ての都市について、別の都市からその都市に向かう」ことを表しています。
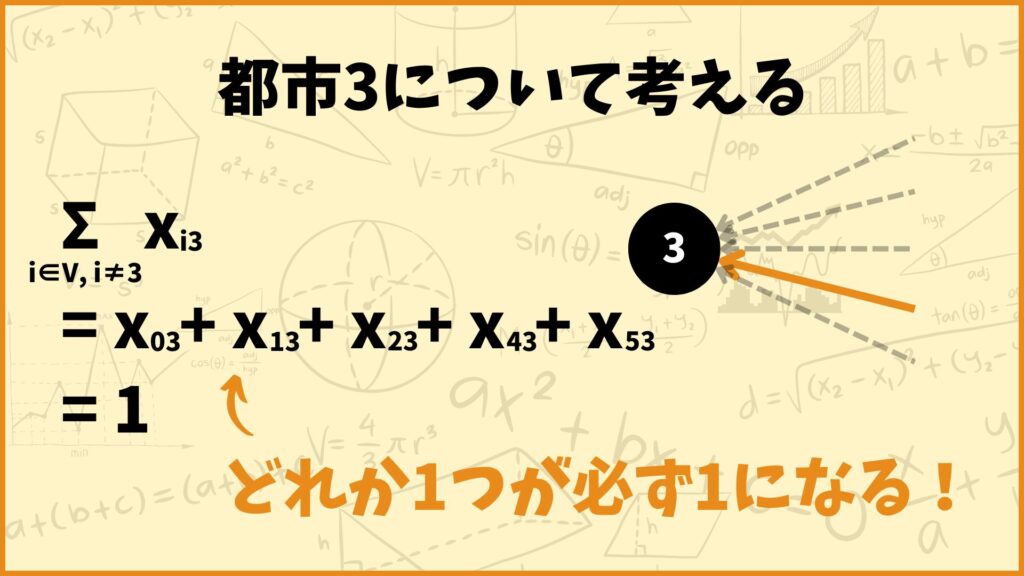
例えば都市3(ソウル)について考えてみましょう。制約式の左辺は
\(\sum\limits_{i \in V, i \ne 3}x_{i3}\)
\( = x_{03} + x_{13} + x_{23} + x_{43} + x_{53}\)
となります。変数\(x_{ij}\)は0か1しか取らないので、制約式が成り立つためには上記の5個の変数のうちどれか1つだけが1を取ることを表します。これは
「必ず他の都市から都市3に向かう」
ということを表しています。例えば\(x_{23} = 1\)としましょう。これは
「都市2(ブエノスアイレス)から都市3(ソウル)に向かう」
ということを表しています。
3つ目の制約
3つ目の制約:
\(\sum\limits_{i \in S}\sum\limits_{j \in S, i \ne j}x_{ij} \leq |S| -1 \;\;\; (\forall S \subset V, |S| \geq 2)\)
3つ目の制約は部分巡回路除去制約です。
この制約は第4節の所で詳しく説明しています。
整数計画問題としてまとめる
以上のことを踏まえて整数計画問題として定式化しましょう。
パラメータ:
\(V = \{0,1,2,3,4,5\}\) : 都市の集合
\(d_{ij}\) : 都市\(i\)と都市\(j\)間の距離
変数:
\(x_{ij} \in \{0,1\}\) : 都市\(i\)から都市\(j\)に向かうなら1、そうでないなら0を取る0-1変数
定式化:
\( \min \;\;\; \sum\limits_{i \in V}\sum\limits_{j \in V , i \ne j} d_{ij}x_{ij}\)
\(\;\text{s.t.}\;\;\;\sum\limits_{j \in V, i \ne j}x_{ij} = 1 \;\;\; (\forall i \in V)\)
\(\;\;\;\;\;\;\;\;\; \sum\limits_{i \in V, i \ne j}x_{ij} = 1 \;\;\; (\forall j \in V)\)
\(\;\;\;\;\;\;\;\;\; \sum\limits_{i \in S}\sum\limits_{j \in S, i \ne j}x_{ij} \leq |S| -1 \;\;\; (\forall S \subset V, |S| \geq 2)\)
\(\;\;\;\;\;\;\;\;\; x_{ij} \in \{0,1\} \;\;\; (\forall i \in V, \forall j \in V, i \ne j)\)
ということで整数計画問題として定式化することができました。
部分巡回路ってなに?
それでは先ほど説明を飛ばした部分巡回路除去制約について説明していきます。今回のようにルートの最適化を考える場合は、部分巡回路というものを考慮する必要があります。
部分巡回路ってなに?
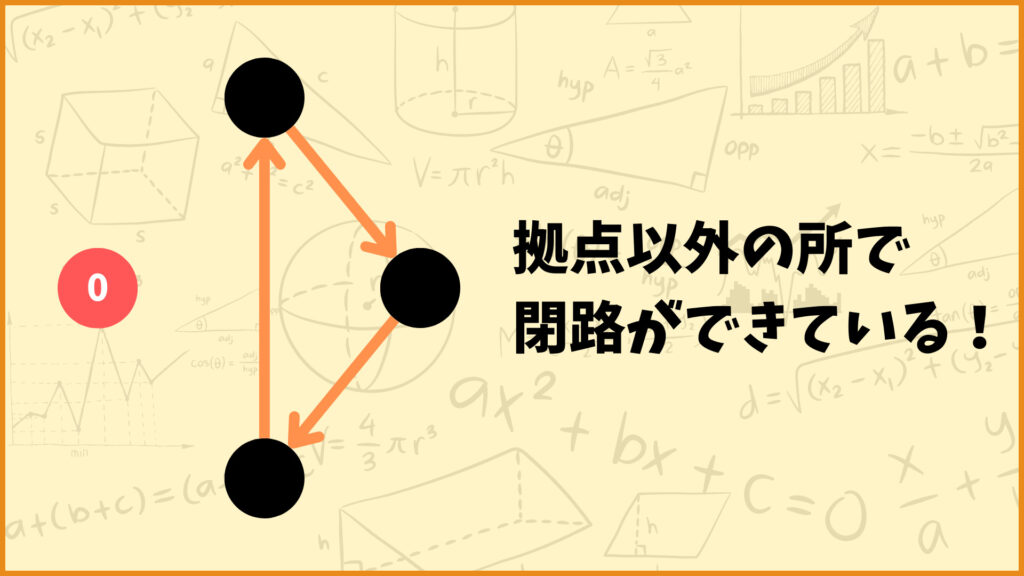
部分巡回路は上図のようなルートです。本来は拠点からスタートして拠点に戻ってくるルートを考えたいのですが、上図は拠点以外の所で閉路ができています。これが部分巡回路です。
旅行ルートの最適化では部分巡回路はできてほしくないので、除去する必要があります。
どうやって部分巡回路を除去する?
部分巡回路除去制約:
\(\sum\limits_{i \in S}\sum\limits_{j \in S, i \ne j}x_{ij} \leq |S| -1 \;\;\; (\forall S \subset V, |S| \geq 2)\)
結論上記の制約で部分巡回路を除去することができます。まず記号の説明をします。\(S\)は都市の集合\(V\)の真部分集合です。例えば\(S = \{1,2\}\)として、部分巡回路を持たないルートと持つルートについてそれぞれ考えてみましょう。
部分巡回路を持たない場合
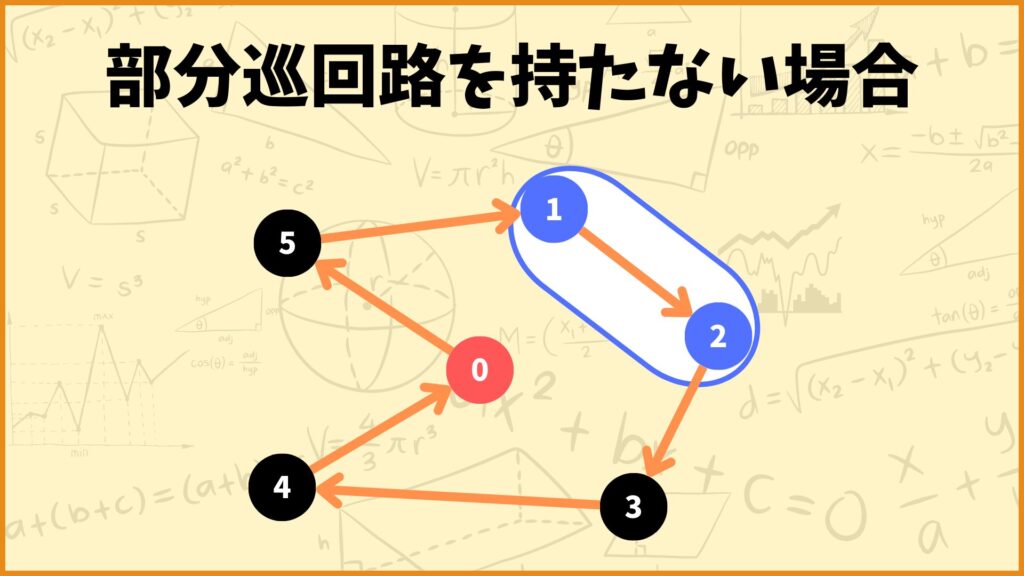
上記のようなルートを考えると、\(x_{12} = 1\)となるので、左辺は
\(\sum\limits_{i \in S}\sum\limits_{j \in S, i \ne j}x_{ij}\)
\( = x_{12} + x_{21}= 1+0 = 1\)
となり、右辺は
\(|S|-1 = 2 -1 =1\)
となるので制約式を満たします。
部分巡回路を持つ場合
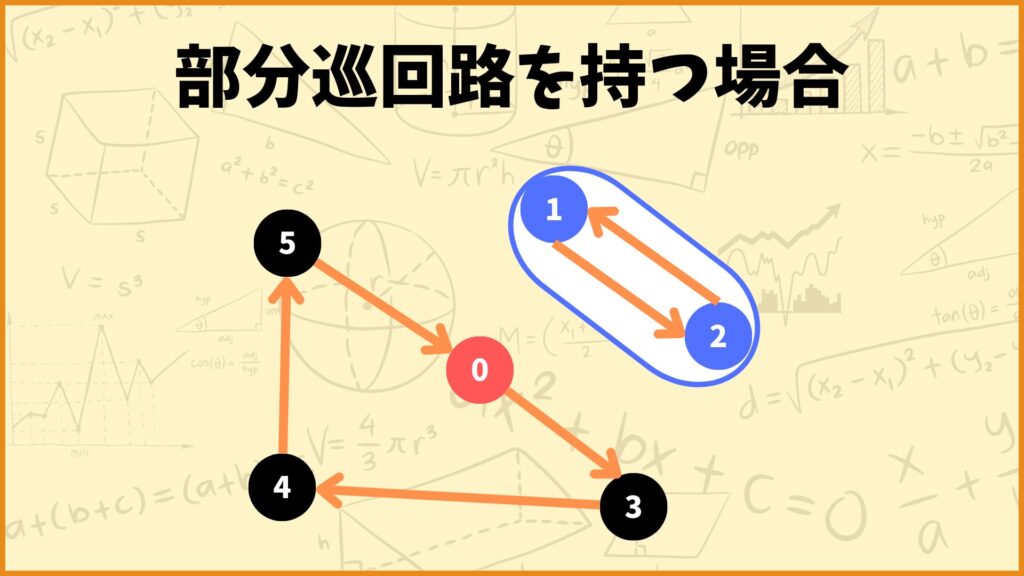
上の例は制約式①,②を満たすルートですが部分巡回路を持っています。(都市1と都市2の間が部分巡回路です)
このとき\(x_{12} = x_{21} = 1\)となり、制約式の左辺は
\(\sum\limits_{i \in S}\sum\limits_{j \in S, i \ne j}x_{ij}\)
\( = x_{12} + x_{21} = 1+1 = 2\)
となり、右辺は
\(|S|-1 = 2 -1 =1\)
となるので制約式を満たしません。
\(|S| \geq 2\)な理由を考えてみましょう。まず\(|S|=0\)は明らかに必要ないですね。次に\(|S|=1\)の場合を考えてみましょう。例えば\(S = \{1\}\)とすると左辺は
\(\sum\limits_{i \in \{1\}}\sum\limits_{j \in \{1\}, i \ne j}x_{iuv}\)
となります。しかしこれは
\(i = 1,j = 1, i \ne j\)
っていう矛盾した式になってしまいます。そのため\(|S| \geq 2\)となります。
部分巡回路除去制約(DFJ制約)の問題点
今回用いた部分巡回路除去制約はDFJ制約と呼ばれます。この制約の問題点は、
「制約の本数がめっちゃ多い」
ということです。もっとちゃんと言うと、旅行で行く都市の数が増えるにつれて制約の本数が指数的に増加してしまうのがDFJ制約の問題点です。制約の本数を数えてみましょう。
制約式の本数は以下の条件を満たす集合\(S\)の総数と同じになります。
\(S \subset V, \; |S| \geq 2.\)
\(V\)の部分集合の総数は\(2^{|V|}\)個あります。
要素数が1の\(V\)の部分集合の総数は\(|V|\)個あり、それらは上記の条件を満たしません。
\(\emptyset,V\)は\(V\)の部分集合で、これも上記の条件を満たしません。
以上より条件を満たす集合\(S\)の総数は
\(2^{|V|} – |V|-2\)
となり、これがDFS制約の本数となります。具体的な本数を求めてみると
\(|V| = 6 \Rightarrow 2^6 – 6 -2 = 56\)本
\(|V| = 10 \Rightarrow 2^{10} – 10-2 = 1012\)本
\(|V| = 15 \Rightarrow 2^{15} – 15-2 = 32751\)本
\(|V| = 20 \Rightarrow 2^{20} – 20-2 = 1048554\)本
制約式の本数が多い分計算時間も長くなってしまいます。今回は\(|V| =6\)なのでそんなに制約式の本数は多くないですが、旅行する都市の数が多くなるとこの定式化では現実的な時間で最適解を求めるのは難しくなります。
部分巡回路除去制約はこの記事で紹介したDFJ制約以外にもMTZ制約などがあります。別の記事でMTZ制約を使った定式化も解説しているのでもしよければそちらも見てみてください!
pythonで解いてみる
それでは実際にこの問題をpythonで解いてみましょう。結論以下のプログラムを実行することで問題を解くことができます。
## 事前準備
from pulp import *
from itertools import chain, combinations## 記号の設定
V = [0,1,2,3,4,5]
# # 各都市間の距離を設定
d = {}
d[0,1] = 10862
d[0,2] = 18388
d[0,3] = 1152
d[0,4] = 9570
d[0,5] = 9575
d[1,2] = 8536
d[1,3] = 11070
d[1,4] = 5577
d[1,5] = 9030
d[2,3] = 19454
d[2,4] = 11142
d[2,5] = 11829
d[3,4] = 8873
d[3,5] = 8498
d[4,5] = 3513
# 距離dを対称にする
for i in V:
for j in V:
if i > j:
d[i,j] = d[j,i]
# Vの真部分集合Sの集合を返す関数を定義
def powerset(iterable):
s = list(iterable)
return list(map(list, chain.from_iterable(combinations(s, r) for r in range(len(s)+1))))
subsets = powerset(V) # Vの真部分集合Sを2次元リスト形式で設定## 整数計画問題として定式化したものを解く
prob = pulp.LpProblem(sense = LpMinimize)
x = LpVariable.dicts("x", [(i, j) for i in V for j in V if i != j], cat="Binary")
prob += lpSum(d[(i,j)] * x[i,j] for i in V for j in V if i != j)
for i in V:
prob += lpSum(x[i,j] for j in V if i != j) == 1
for j in V:
prob += lpSum(x[i,j] for i in V if i != j) == 1
for S in subsets:
if 2 <= len(S) < len(V):
prob += lpSum(x[i,j] for i in S for j in S if i != j) <= len(S) - 1
result = prob.solve()
## 結果の表示
print(LpStatus[result]) # 解の状態を表示
# 最適解の表示(値が1の変数だけ表示)
for i in V:
for j in V:
if i != j:
if x[i,j].value() == 1:
print(f"x_{i}_{j} =", x[i,j].value())
print("最適値 :",prob.objective.value()) # 最適値の表示
これらのプログラムを実行したら上の結果が得られました。それでは1つずつ説明していきます。
プログラムの説明
事前準備
## 事前準備
from pulp import *
from itertools import chain, combinations
問題を解く前に事前準備をしましょう。pulpはpythonで数理計画問題を解くのに使います。itertoolsは部分集合\(S\)を作るときに使います。
記号の設定
## 記号の設定
V = [0,1,2,3,4,5]
# # 各都市間の距離を設定
d = {}
d[0,1] = 10862
d[0,2] = 18388
d[0,3] = 1152
d[0,4] = 9570
d[0,5] = 9575
d[1,2] = 8536
d[1,3] = 11070
d[1,4] = 5577
d[1,5] = 9030
d[2,3] = 19454
d[2,4] = 11142
d[2,5] = 11829
d[3,4] = 8873
d[3,5] = 8498
d[4,5] = 3513
# 距離dを対称にする
for i in V:
for j in V:
if i > j:
d[i,j] = d[j,i]
# Vの真部分集合Sの集合を返す関数を定義
def powerset(iterable):
s = list(iterable)
return list(map(list, chain.from_iterable(combinations(s, r) for r in range(len(s)+1))))
subsets = powerset(V) # Vの部分集合Sを2次元リスト形式で設定
次に記号の設定の所を説明します。
2行目では都市の集合を設定しています。各数字が表している年は以下の通りです。
0 : 東京
1 : ニューヨーク
2 : ブエノスアイレス
3 : ソウル
4 : ロンドン
5 : カイロ
5~20行目では各都市間の距離を設定しています。単位はkmで距離の計算は以下のサイトで行っています。
2都市間の距離と方位角 – 高精度計算サイト (casio.jp)
22~26行目では\(d_{ij} = d_{ji}\)と設定しています。
28~33行目ではVの冪集合を求めています。イメージとしてはVの部分集合を全部持ってきたみたいな感じです。
整数計画問題として定式化したものを解く
## 整数計画問題として定式化したものを解く
prob = pulp.LpProblem(sense = LpMinimize)
x = LpVariable.dicts("x", [(i, j) for i in V for j in V if i != j], cat="Binary")
prob += lpSum(d[(i,j)] * x[i,j] for i in V for j in V if i != j)
for i in V:
prob += lpSum(x[i,j] for j in V if i != j) == 1
for j in V:
prob += lpSum(x[i,j] for i in V if i != j) == 1
for S in subsets:
if 2 <= len(S) < len(V):
prob += lpSum(x[i,j] for i in S for j in S if i != j) <= len(S) - 1
# 問題を解く
result = prob.solve()
## 結果の表示
print(LpStatus[result]) # 解の状態を表示
# 最適解の表示(値が1の変数だけ表示)
for i in V:
for j in V:
if i != j:
if x[i,j].value() == 1:
print(f"x_{i}_{j} =", x[i,j].value())
print("最適値 :",prob.objective.value()) # 最適値の表示
2行目で問題を最小化に設定しています。
4行目で0-1変数\(x_{ij}\)の定義をしています。\(i \ne j\)にしたいのでif i != jとしています。これ以降に出てくるif i != jはすべて同じ意味です。
6行目で目的関数を設定しています。
8~16行目で制約条件を設定しています。
18~19行目で問題を解いています。
21~31行目で結果を表示しています。22行目で解の状態、25~29行目で最適解、31行目で最適値をそれぞれ表示しています。
結果の解釈

1行目が解の状態、2~7行目は最適解を表しています。8行目が最適値を表しています。Optimalと表示されているのでちゃんと最適解が得られていることが分かります。
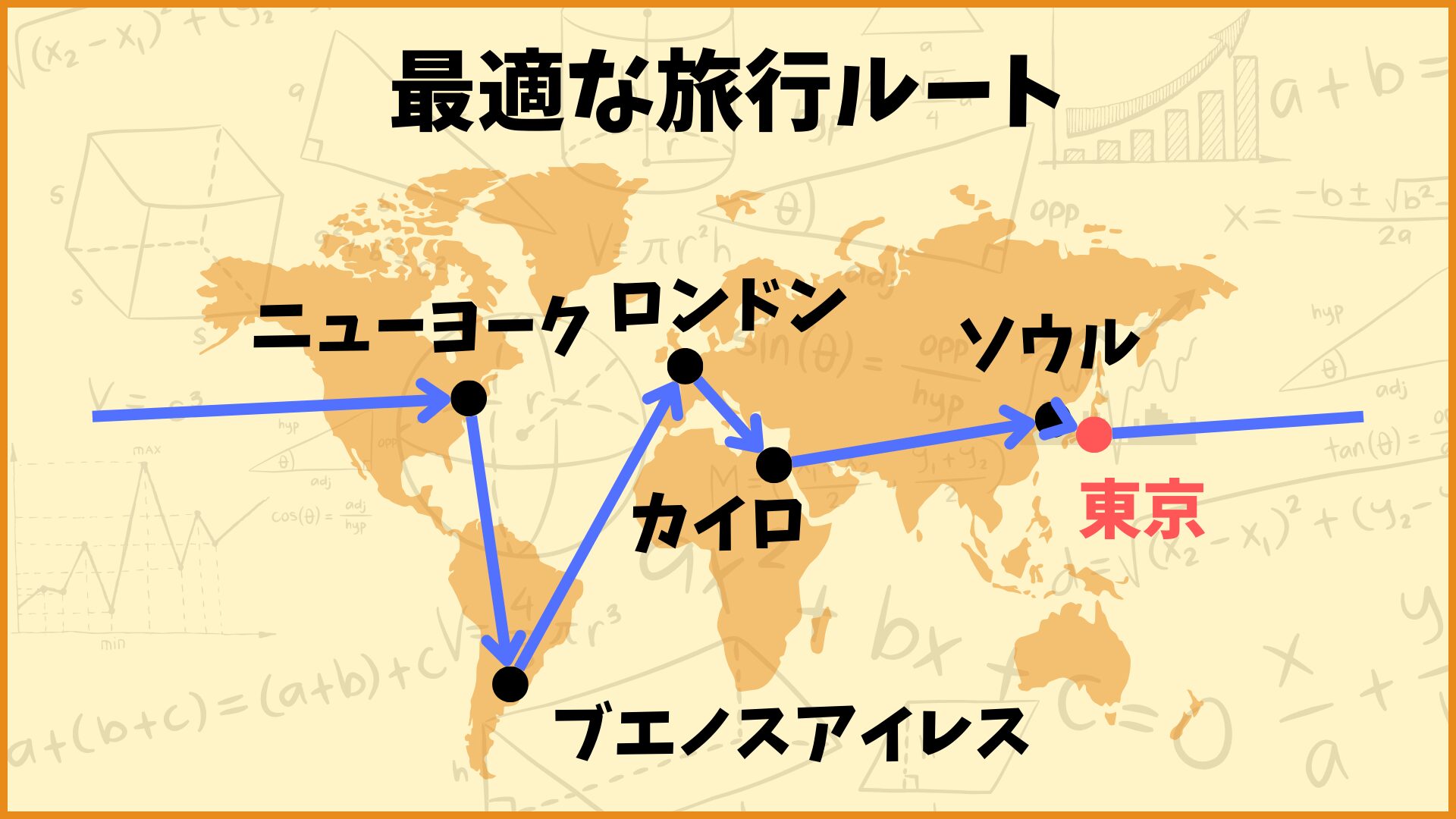
最適解を見ると、
0(東京)→1(ニューヨーク)→2(ブエノスアイレス)
→4(ロンドン)→5(カイロ)→3(ソウル)→0(東京)
というルートが最も移動距離の合計が短い旅行ルートということが分かりました。
おわりに
いかがでしたか。
今回の記事では巡回セールスマン問題について解説していきました。
今後もこのような数理最適化に関する記事を書いていきます!
最後までこの記事を読んでくれてありがとうございました。




