こんにちは!しゅんです!
この記事では頂点被覆問題について説明します。
この記事では頂点被覆問題がどんな問題なのか、そして頂点被覆問題を整数計画問題として定式化してpythonで解く方法を解説したいと思います。
それではやっていきましょう!
普段は組合せ最適化の記事を書いてたりします。
ぜひ他の記事も読んでみてください!
このブログの簡単な紹介はこちらに書いてあります。
興味があったら見てみてください。
このブログでは経営工学を勉強している現役理系大学生が、経営工学に関することを色々話していきます!
ぼくが経営工学を勉強している中で感じたことや、興味深かったことを皆さんと共有出来たら良いなと思っています。
そもそも経営工学とは何なのでしょうか。Wikipediaによると
経営工学(けいえいこうがく、英: engineering management)は、人・材料・装置・情報・エネルギーを総合したシステムの設計・改善・確立に関する活動である。そのシステムから得られる結果を明示し、予測し、評価するために、工学的な分析・設計の原理・方法とともに、数学、物理および社会科学の専門知識と経験を利用する。
引用元 : 経営工学 – Wikipedia
長々と書いてありますが、要は経営、経済の課題を理系的な観点から解決する学問です。
頂点被覆問題ってなに?
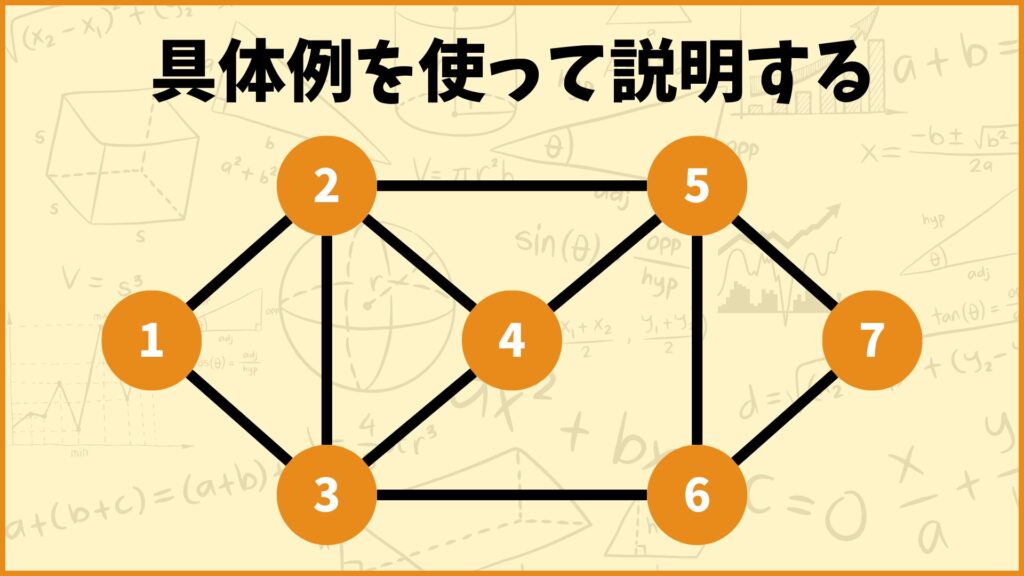
上のグラフを使って頂点被覆問題について説明していきます。
頂点被覆ってなに?
まず最初に頂点被覆って何なのかについて説明したいと思います。グラフから適当に1つ頂点を選んでみましょう。
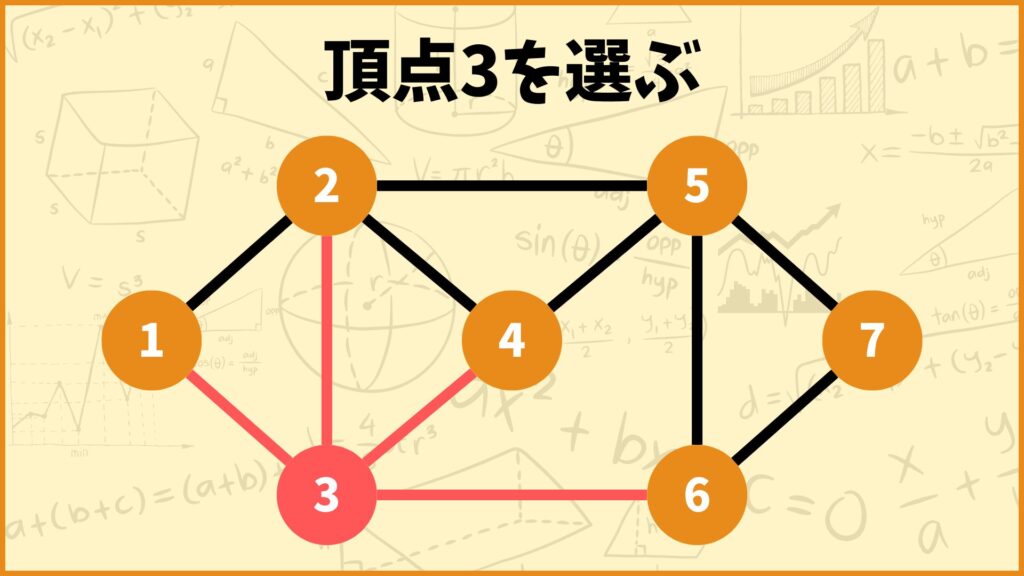
上の例では頂点3を選びました。頂点3に接続する辺は辺\((1,3),(2,3),(3,4),(3,6)\)の4つなので、これらの辺を赤色に塗っておきました。このように選んだ頂点に接続する辺を赤色に塗っていくという操作を続けていきます。
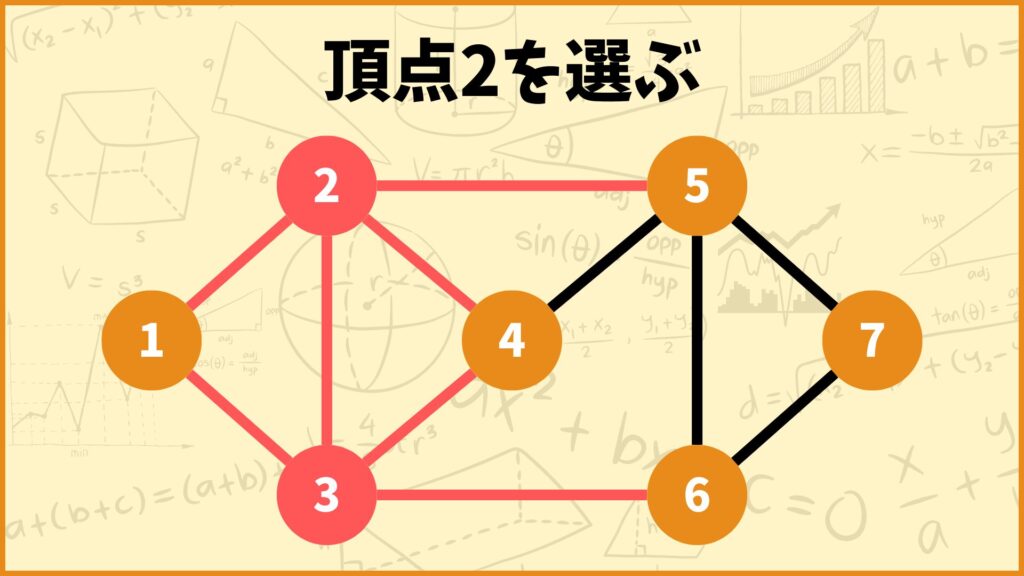
次に頂点2を選んでみました。頂点2に接続する辺は辺\((2,1),(2,3),(2,4),(2,5)\)の4つなのでこれらの辺を赤色に塗っておきます。
辺\((2,3)\)は既に赤色に塗られているので特に何も操作する必要はないです。
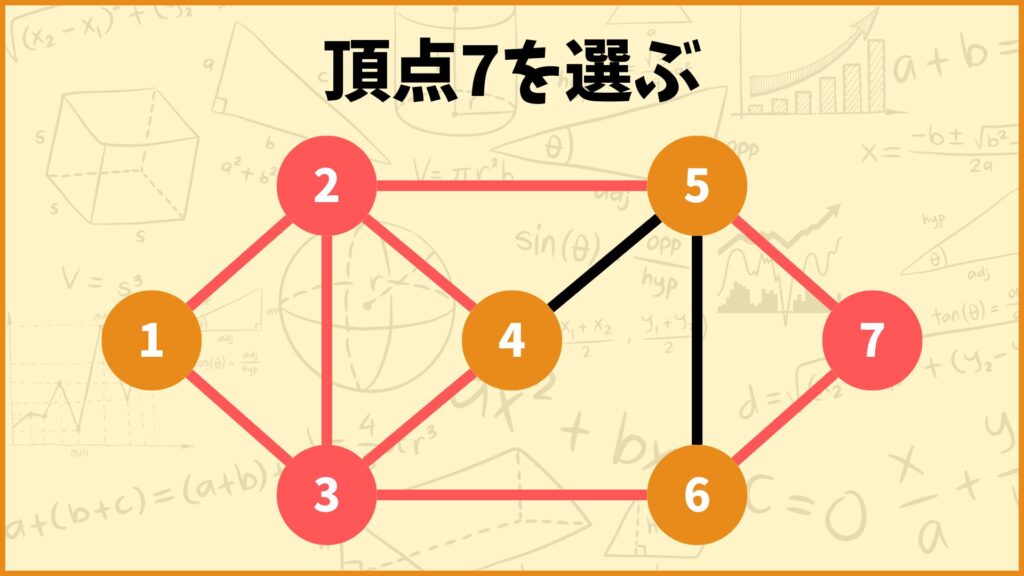
次に頂点7を選んでみました。頂点7に接続する辺は辺\((5,7),(6,7)\)の2つなのでこれらの辺を赤色に塗りました。
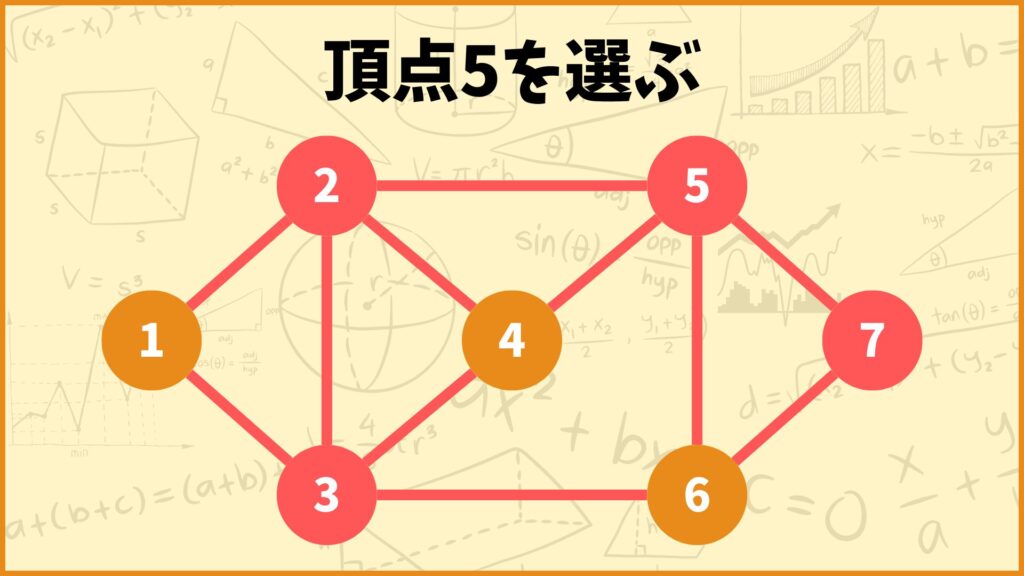
次に頂点5を選んでみました。頂点5に接続する辺は辺\((2,5),(4,5),(5,6)\)なのでこれらの辺を赤色に塗っておきます。
辺\((2,5)\)は既に赤色に塗られているので特に何も操作する必要はないです。
この時点で全ての辺が赤色に塗られましたね。このようにいくつかの頂点を選んだとき、グラフ中のすべての辺が選んだ頂点のいずれかと接続する場合、選んだ頂点集合のことを頂点被覆と言います。
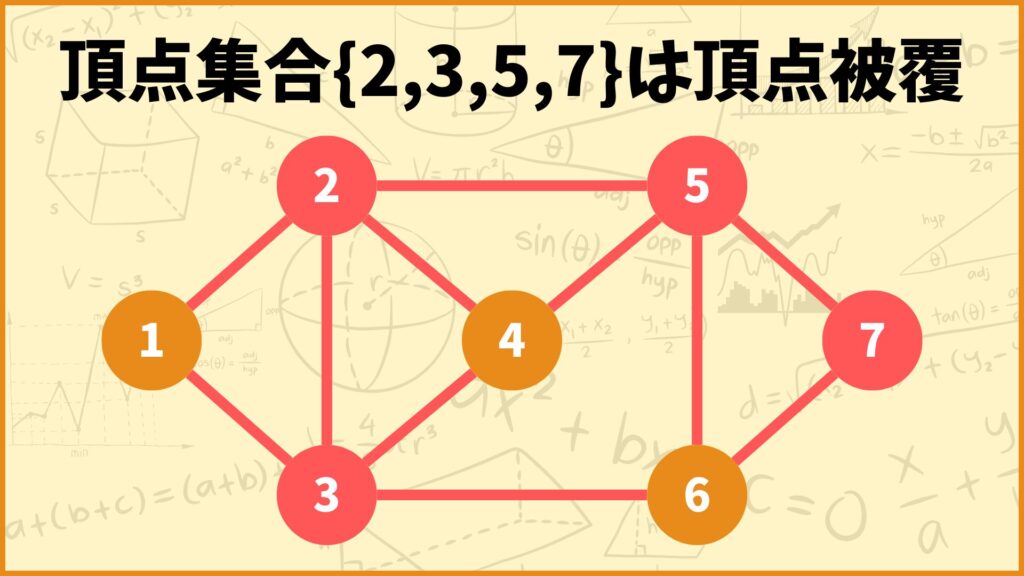
今回用いた例で言うと頂点集合\(\{2.3.5.7\}\)は頂点被覆となります。上のグラフの場合、頂点被覆は他にもたくさんあります。
頂点被覆をちゃんと説明すると以下のようになります。
無向グラフ\(G = (V,E)\)が与えられたとき、グラフ\(G\)の頂点被覆とは以下の条件を満たす頂点集合\(C \subseteq V\)である。
「グラフ中の任意の辺\(e \in E\)が\(C\)中の少なくとも1つの頂点と接続する。」
最小頂点被覆問題ってなに?
次に最小頂点被覆問題がどんな問題なのかを説明します。いま各頂点にコストが設定されているとします。今回は頂点番号がその頂点のコストとします。
頂点1のコストは1
頂点2のコストは2
…
頂点7のコストは7
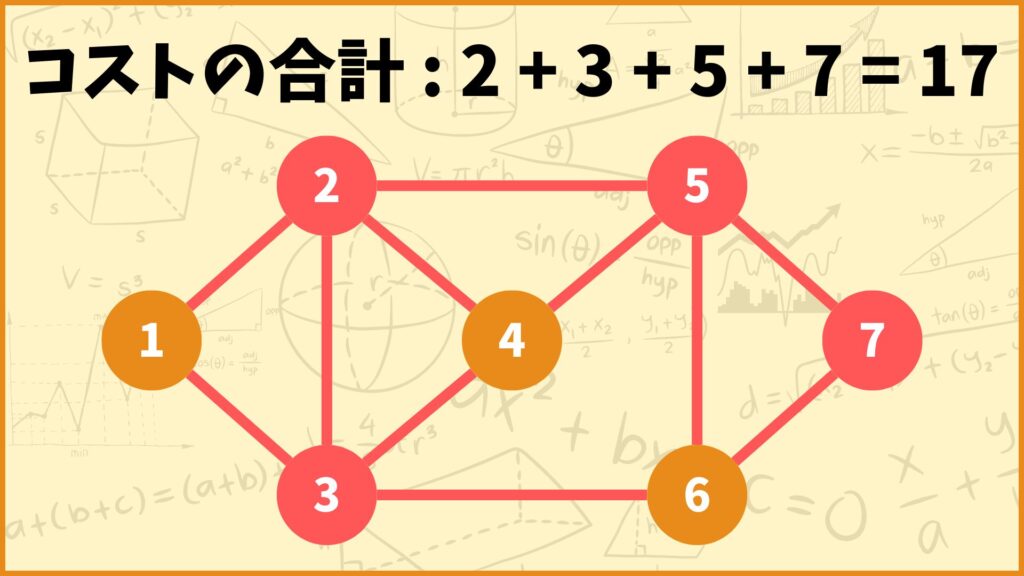
そうすると上の頂点被覆のコストの合計は
\(2+3+5+7 = 17\)
となります。では上の頂点被覆は全ての頂点被覆の中でコストの合計が最小となるものでしょうか。これを求める問題が最小頂点被覆問題です。
最小頂点被覆問題をちゃんと説明すると以下のようになります。
グラフ\(G\)中の各頂点\(i \in V\)に対してコスト\(c_{i}\)が与えられているとする。\(G\)における頂点被覆\(C\)のうち、\(\sum\limits_{i \in C}c_{i}\)が最小となるようなものを求める問題。
これ以降、最小頂点被覆問題を頂点被覆問題と呼びます。
頂点被覆問題を整数計画問題として定式化する
それでは次に頂点被覆問題を整数計画問題として定式化する方法を説明します。「記号の定義」、「目的関数の設定」、「制約条件の設定」の3つに分けてそれぞれ説明したいと思います。
記号の定義
パラメータ:
\(V\) : 頂点集合
\(E\) : 辺集合
\(c_{i}\) : 頂点\(i\)のコスト
変数:
\(x_{i} \in \{0,1\}\) : 頂点\(i\)を選ぶなら1、選ばないなら0を取る0-1変数
パラメータとして頂点集合\(V\)、辺集合\(E\)、頂点\(i\)のコスト\(c_{i}\)を設定します。

上の例で言うと
\(V = \{1,2,3,4,5,6,7\}\)
\(E = \{(1,2),(1,3),(2,3),(2,4),(2,5),(3,4),(3,6),(4,5),(5,6),(5,7),(6,7)\}\)
となります。各頂点のコストの値は頂点番号と同じにします。すなわち
\(c_{1} = 1, c_{2} = 2,c_{3} = 3\)
\(c_{4} = 4, c_{5} = 5, c_{6} = 6, c_{7} = 7\)
となります。変数は頂点\(i\)を選ぶなら1、そうでないなら0を取る0-1変数\(x_{i}\)を使います。上の例で言うと
\(x_{2} = x_{3} = x_{5} = x_{7}=1\)
となります。
目的関数の設定
目的関数:
\(\sum\limits_{i \in V}c_{i}x_{i}\)
頂点被覆問題の目的は
「頂点被覆の中でコストの合計が最小なものを求める」
というものです。

上の頂点被覆の例でいうと
\(x_{2} = x_{3} = x_{5} = x_{7}=1\)
となるので目的関数値は
\(\sum\limits_{i \in V}c_{i}x_{i} = c_{2} + c_{3} + c_{5} + c_{7} = 17\)
となり、これは上の頂点被覆のコストの合計となっていますね。今回はこれが最小となる場合を求めたいので問題を\(\text{minimize}\)に設定します。
目的関数を最小化:
\(\min \;\; \sum\limits_{i \in V}c_{i}x_{i}\)
制約条件の設定
制約条件:
\(x_{i} + x_{j} \geq 1 \;\;\; (\forall (i,j) \in E)\)
制約条件は
「選んだ頂点からなる集合が頂点被覆になっている」
ことです。
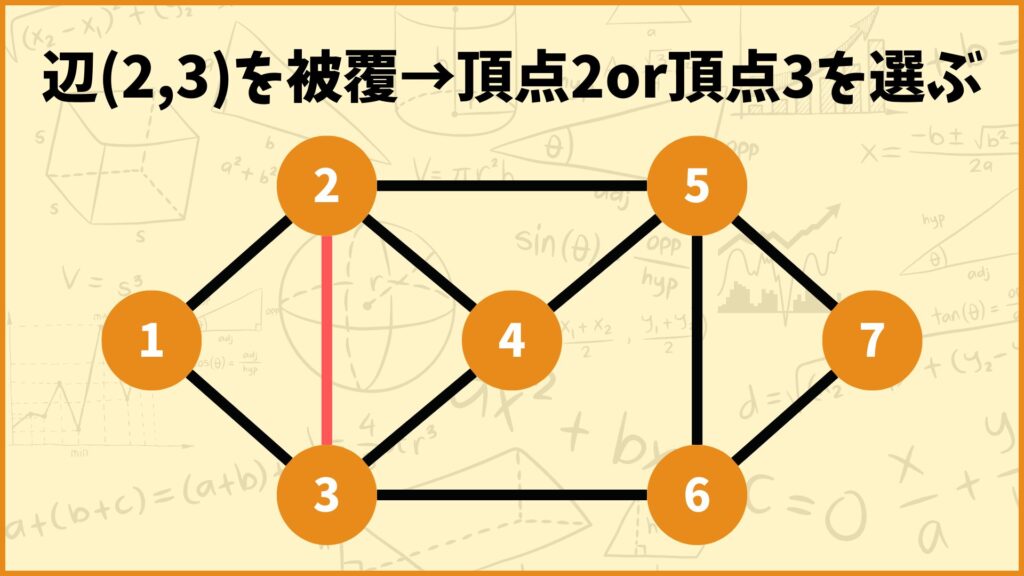
例えば上のグラフに対して辺\((2,3)\)を被覆したいとします。辺\((2,3)\)を被覆するためには頂点2か頂点3のどちらかを必ず選ぶ必要があります。つまり\(x_2\)と\(x_3\)のうち少なくともどっちかが1じゃないといけないです。
このことを式で表すと以下のようになります。
\(x_2 + x_3 \geq 1\)
上の式は\((x_2,x_3) = (0,1),(1,0),(1,1)\)のいずれかであることを表しています。もう少し一般的に考えてみましょう。グラフ中の辺\((i,j)\)を被覆するためには\(x_i\)と\(x_j\)のうち少なくともどっちかが1じゃないといけないです。
このことを式で表すと以下のようになります。
\(x_i + x_j \geq 1\)
この式が全ての辺\((i,j) \in E\)で成り立っている必要があります。
制約条件:
\(x_{i} + x_{j} \geq 1 \;\;\; (\forall (i,j) \in E)\)
整数計画問題としてまとめる
以上のことを踏まえて整数計画問題として定式化しましょう。
パラメータ:
\(V\) : 頂点集合
\(E\) : 辺集合
\(c_{i}\) : 頂点\(i\)のコスト
変数:
\(x_{i} \in \{0,1\}\) : 頂点\(i\)を選ぶなら1、選ばないなら0を取る0-1変数
定式化:
\( \min \;\;\; \sum\limits_{i \in V}c_{i}x_{i}\)
\(\;\text{s.t.}\;\;\;x_{i} + x_{j} \geq 1 \;\;\; (\forall (i,j) \in E)\)
\(\;\;\;\;\;\;\;\;\; x_{i} \in \{0,1\} \;\;\; (\forall i \in V)\)
ということで整数計画問題として定式化することができました。
pythonで解いてみた
それでは実際にこの問題をpythonで解いてみましょう。結論以下のプログラムを実行することで問題を解くことができます。
## 事前準備
from pulp import * # pulpのインポート
## 記号の設定
V = [1,2,3,4,5,6,7] # 頂点集合の設定
E = [(1,2),(1,3),(2,3),(2,4),(2,5),(3,4),(3,6),(4,5),(5,6),(5,7),(6,7)] # 辺集合の設定
c = {1:1,
2:2,
3:3,
4:4,
5:5,
6:6,
7:7} # 各頂点のコストの設定
## 整数計画問題として定式化して解く
prob = pulp.LpProblem(sense = LpMinimize) # 問題を最小化に設定
x = LpVariable.dicts("x",V, cat="Binary") # 変数の設定
prob += lpSum(c[i] * x[i] for i in V) # 目的関数の設定
for (i,j) in E:
prob += x[i] + x[j] >= 1 # 制約条件の設定
result = prob.solve() # 問題を解く
## 結果の表示
print("解の状態 :",LpStatus[result]) # 解の状態を表示(optimalなら最適解が得られてる)
print("最適値 :",prob.objective.value()) # 最適値の表示
for i in V:
if x[i].value() == 1:
print(f"x_{i} =", x[i].value()) # 最適解(値が1の変数)の表示
これらのプログラムを実行したら上の結果が得られました。それではコードが何を表しているのか1つずつ解説していきます。
コードの解説
「事前準備」、「記号の設定」、「整数計画問題として定式化して解く」、「結果の表示」の4つに分けてそれぞれ解説していきます。
事前準備
## 事前準備
from pulp import * # pulpのインポート
pulpはpythonで整数計画問題を扱うのに便利なライブラリです。インストールしていない場合はインストールする必要があります。
!pip install pulp # pulpのインストール 記号の設定
## 記号の設定
V = [1,2,3,4,5,6,7] # 頂点集合の設定
E = [(1,2),(1,3),(2,3),(2,4),(2,5),(3,4),(3,6),(4,5),(5,6),(5,7),(6,7)] # 辺集合の設定
c = {1:1,
2:2,
3:3,
4:4,
5:5,
6:6,
7:7} # 各頂点のコストの設定
2行目で頂点集合をリスト形式で設定しています。今回は頂点1から頂点7まであるので上のようなリストを作成しました。
3行目で辺集合をリスト形式で設定しています。
4行目で各頂点のコストを辞書形式で設定しています。
整数計画問題として定式化して解く
## 整数計画問題として定式化して解く
prob = pulp.LpProblem(sense = LpMinimize) # 問題を最小化に設定
x = LpVariable.dicts("x",V, cat="Binary") # 変数の設定
prob += lpSum(c[i] * x[i] for i in V) # 目的関数の設定
for (i,j) in E:
prob += x[i] + x[j] >= 1 # 制約条件の設定
result = prob.solve() # 問題を解く
2行目で問題を最小化に設定しています。「sense = LpMaximize」だと目的関数を最大化する問題に設定できます。
4行目で変数を設定しています。「LpVariable.dicts()」は変数をいっぺんに設定できるので変数が多いときに便利です。括弧の中身は左から順に(”変数名”, 添字の集合, 変数の種類)となっています。
変数\(x_i\)の添字\(i\)は頂点集合\(V\)中の要素なので添字の集合はVとします。
「cat = “Binary”」で変数を0-1変数に設定しています。連続変数にしたければ「cat = “Continuous”」とすれば良いです。
6行目で目的関数を設定しています。pulpで\(\sum\)は「lpSum」で表現できます。「c[i] * x[i]」と設定することで\(c_ix_i\)、「for i in V」と設定することで\(i \in V\)を表現できます。
8~9行目で制約条件を設定しています。「for (i,j) in E」で\(\forall (i,j) \in E\)を表しています。
「prob += x[i] + x[j] >= 1」で\(x_i + x_j \geq 1\)を表しています。
11行目で問題を解いています。問題を解くときは「.solve()」でできます。
結果の表示
## 結果の表示
print("解の状態 :",LpStatus[result]) # 解の状態を表示(Optimalと表示されたら最適解が得られてる)
print("最適値 :",prob.objective.value()) # 最適値の表示
for i in V:
if x[i].value() == 1:
print(f"x_{i} =", x[i].value()) # 最適解(値が1の変数)の表示
2行目で解の状態を表示しています。Optimalと表示されたら最適解が得られています。
3行目で最適値を表示しています。
4~6行目で最適解を表示しています。値が1の変数だけ表示するようにしています。
結果の解釈

上記のプログラムを実行したら上のような結果が得られました。1つずつ見ていきます。
1行目は解の状態を表しています。Optimalと表示されているので最適解が得られています。
2行目は最適値を表しています。今回の頂点被覆問題の最適値は16であることが分かりました。
3~6行目は最適解を表しています。これを見ると頂点2,3,5,6を選ぶのが最適であることが分かります。
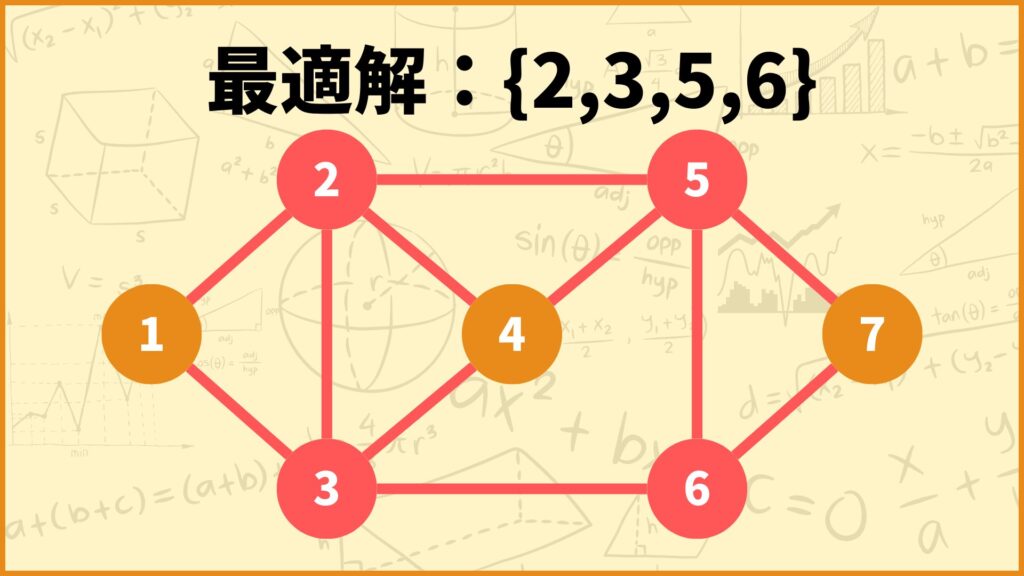
確かに頂点被覆になっていますね。例えば辺\((4,5)\)は頂点5と接続しているので被覆されています。
頂点数をもっと増やしてみた
それでは最後に頂点数をもっと増やして頂点被覆問題を解いてみたいと思います。
グラフを描画してみた
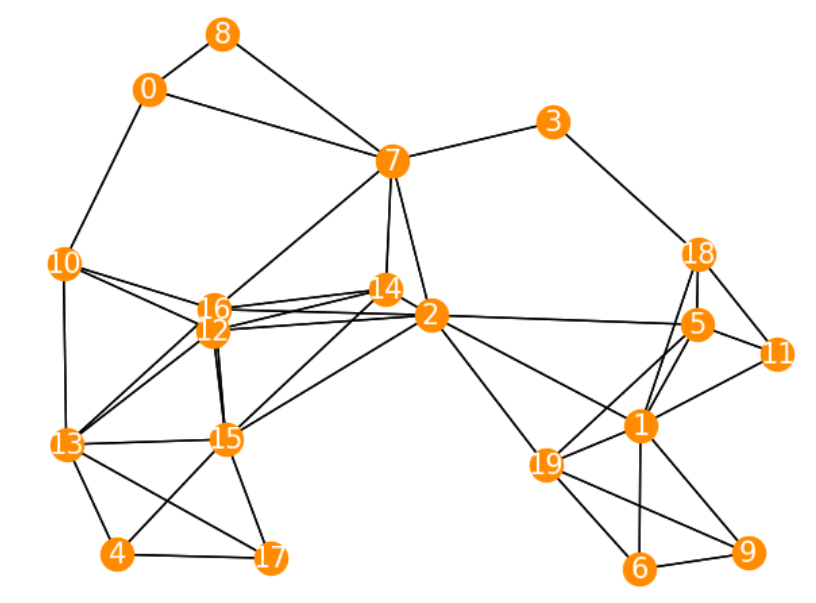
頂点数は20個、各頂点は\([0,10] \times [0,10]\)の2次元ユークリッド平面上にランダムに配置しました。また頂点\(i\)と頂点\(j\)間のユークリッド距離が3.5以下の場合に辺\((i,j)\)が存在するようにしました。
上のグラフを表示するコードは以下の通りです。本題ではないので説明は省略します。
import networkx as nx # networkxのインポート
import matplotlib.pyplot as plt # matplotlibのインポート
import random # randomのインポート
random.seed(1) # ランダム値の固定
V = [i for i in range(20)] # 頂点集合を設定(頂点数は20)
E = [] # 辺集合の初期設定
Pos = {} # 各頂点の座標の初期設定
for i in V:
Pos[i] = [random.uniform(0,10),random.uniform(0,10)] # 各頂点の座標を[0,10]×[0,10]上の2次元ユークリッド平面上にランダムに配置
# グラフの初期化
G = nx.DiGraph()
# 頂点を追加
for v, pos in Pos.items():
G.add_node(v, pos=pos)
# 辺を追加
for i in V:
for j in V:
if i != j:
if ((Pos[i][0] - Pos[j][0])**2 + (Pos[i][1] - Pos[j][1])**2)**(1/2) <= 3.5: # 距離が3.5以下の辺だけグラフに追加
G.add_edge(i, j)
E.append((i,j))
# グラフの描画
pos = nx.get_node_attributes(G, 'pos')
nx.draw(G, pos, with_labels=True, node_color='darkorange', node_size=300,font_size = 15, font_color="white", arrows = False, edge_color = "black")
plt.show()頂点被覆問題を解いてみた
簡単のため各頂点のコストは全て1としました。つまり頂点被覆として選ぶ頂点の数をできるだけ少なくしたいというのが目的関数になります。コードは目的関数のところ以外は先ほどと同じです。
## 整数計画問題として定式化
prob = pulp.LpProblem(sense = LpMinimize) # 問題を最小化に設定
x = LpVariable.dicts("x",V, cat="Binary") # 変数の設定
prob += lpSum(x[i] for i in V) # 目的関数の設定
for (i,j) in E:
prob += x[i] + x[j] >= 1 # 制約条件の設定
result = prob.solve() # 問題を解く
## 結果の表示
print("解の状態 :",LpStatus[result]) # 解の状態を表示(optimalなら最適解が得られてる)
print("最適値 :",prob.objective.value()) # 最適値の表示
for i in V:
if x[i].value() == 1:
print(f"x_{i} =", x[i].value()) # 最適解(値が1の変数)の表示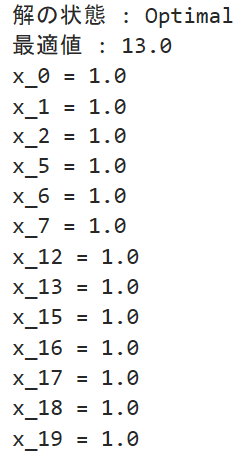
頂点被覆問題を解いたら上のような結果が得られました。最適値が13なので計13個の頂点を選んだらしいです。3行目からは選んだ頂点を表示していますが、多すぎてよく分からないので図示してみましょう。
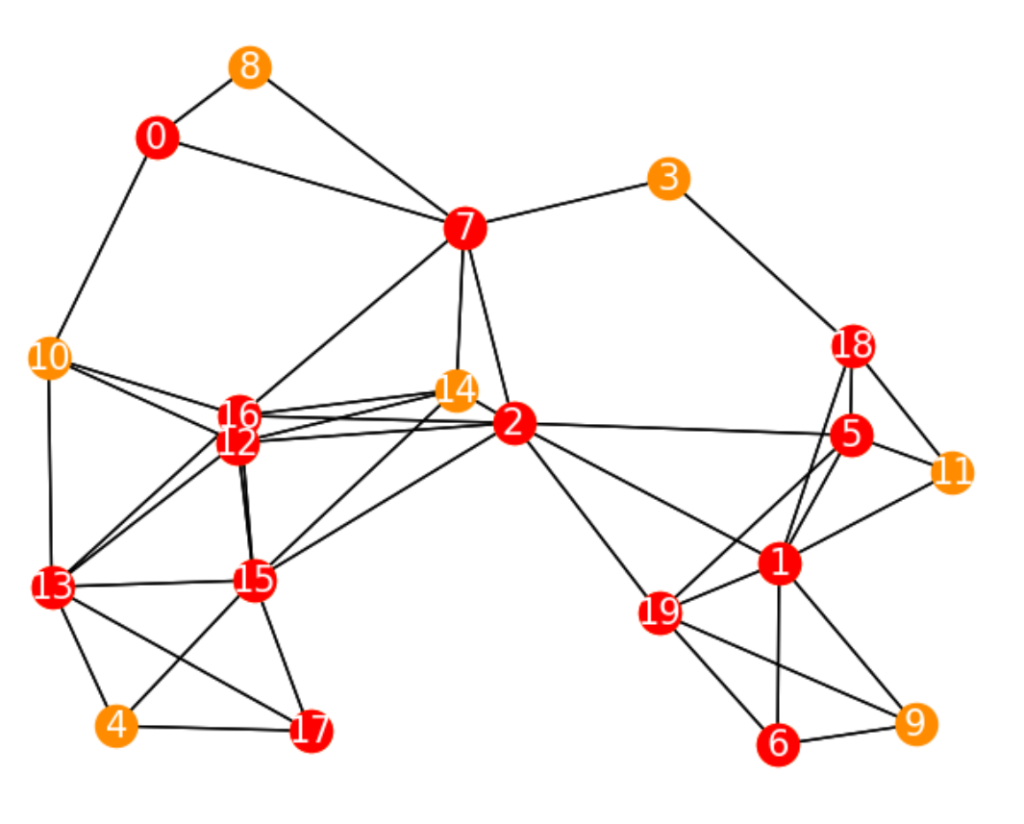
選ばれた頂点は赤色にしました。上記の頂点被覆が要素数最小の頂点被覆だと分かりました。
上のグラフを描画するコードは以下の通りです。
# グラフの初期化
G = nx.DiGraph()
# 頂点を追加
for v, pos in Pos.items():
G.add_node(v, pos=pos)
# 辺を追加
for i in V:
for j in V:
if i != j:
if ((Pos[i][0] - Pos[j][0])**2 + (Pos[i][1] - Pos[j][1])**2)**(1/2) <= 3.5:
G.add_edge(i, j)
E.append((i,j))
# グラフの描画
pos = nx.get_node_attributes(G, 'pos')
nx.draw(G, pos, with_labels=True, node_color='darkorange', node_size=300,font_size = 15, font_color="white", arrows = False, edge_color = "black")
for i in V:
if x[i].value() == 1:
nx.draw_networkx_nodes(G, pos, nodelist=[i], node_color='red', node_size=300)
plt.show()おわりに
いかがでしたか。
今回の記事では頂点被覆問題について解説していきました。
今後もこのような組合せ最適化に関する記事を書いていきます!
最後までこの記事を読んでくれてありがとうございました。




