- データ分析に興味がある人
- 時系列予測を勉強したい人
- SARIMAXを使ってみたい人
こんにちは!しゅんです!
この記事ではSARIMAXを使って時系列予測をしてみたいと思います!
時系列予測の勉強をしていて、SARIMAXを使ってみたいな~と思ってデータを探していたんですが、そういえば自分のブログのデータがあるじゃんと思ったので、今回は「ゆかしゅんぶろぐ」の記事クリック数を予測するSARIMAXモデルをpythonで作っていこうと思います。
普段は組合せ最適化の記事を書いてたりします。
ぜひ他の記事も読んでみてください!
このブログの簡単な紹介はこちらに書いてあります。
興味があったら見てみてください。
このブログでは経営工学を勉強している現役理系大学生が、経営工学に関することを色々話していきます!
ぼくが経営工学を勉強している中で感じたことや、興味深かったことを皆さんと共有出来たら良いなと思っています。
そもそも経営工学とは何なのでしょうか。Wikipediaによると
経営工学(けいえいこうがく、英: engineering management)は、人・材料・装置・情報・エネルギーを総合したシステムの設計・改善・確立に関する活動である。そのシステムから得られる結果を明示し、予測し、評価するために、工学的な分析・設計の原理・方法とともに、数学、物理および社会科学の専門知識と経験を利用する。
引用元 : 経営工学 – Wikipedia
長々と書いてありますが、要は経営、経済の課題を理系的な観点から解決する学問です。
分析に用いるデータ
- データの種類:ゆかしゅんぶろぐの記事クリック数
- 期間:2023年8月30日~2024年12月29日(16カ月)
- データの個数:488個
- データの提供元:google search console
- ブログのジャンル:大学生向けの技術ブログ
plt.figure(figsize = (12,6))
plt.plot(df["クリック数"])
plt.show()
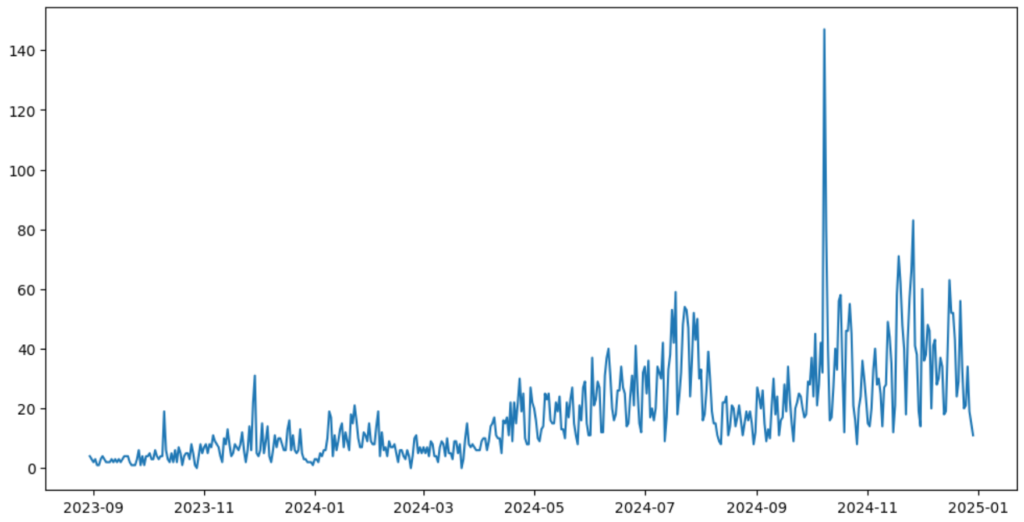
今回分析に用いるデータはgoogle search consoleから得られた「ゆかしゅんぶろぐ」の記事クリック数のデータです。
データの特徴を見る
それではまず最初にデータにどんな特徴があるのかを見てみます。
自己相関を見てみたい!
まず最初に自己相関と偏自己相関を見てこのデータの特徴を調べていきます。
from statsmodels.graphics.tsaplots import plot_acf, plot_pacf
# 自己相関と偏自己相関のプロット
plt.figure(figsize=(12, 6))
plot_acf(df["クリック数"], lags=30, ax=plt.subplot(121)) # 自己相関
plot_pacf(df["クリック数"], lags=30, ax=plt.subplot(122)) # 偏自己相関
plt.tight_layout()
plt.show()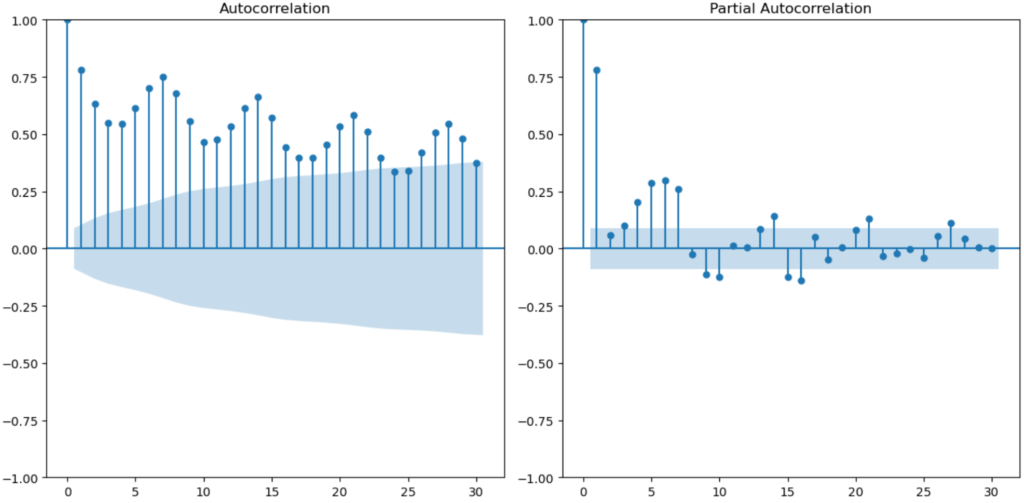
左図が自己相関のコレログラムです。これを見ると7日ごとに山ができていることが分かります。この情報はSARIMAXの季節性のパラメータを決定する際に参考にできます。
このデータは7日周期である
右図は偏自己相関のコレログラムですが、これを見るとラグが1日までは高い値となっており、ラグが2日になると一気に0に近い値を取っていますね。この情報は自己回帰のパラメータを決定する際に参考にできます。
このデータは1日前の値との相関が強い
この分析から分かること:
・データが7日周期である
・1日前のデータとの相関が高い
定常性があるか確認したい!
定常性とは…
時系列データの統計的な特性(平均、分散、自己相関など)が時間によらず一定であるという性質
それでは次にデータの定常性を調べてみます。と言っても原系列(もとの時系列データ)はグラフを見た感じ明らかに定常ではなさそうです。
グラフを見て定常性を調べる
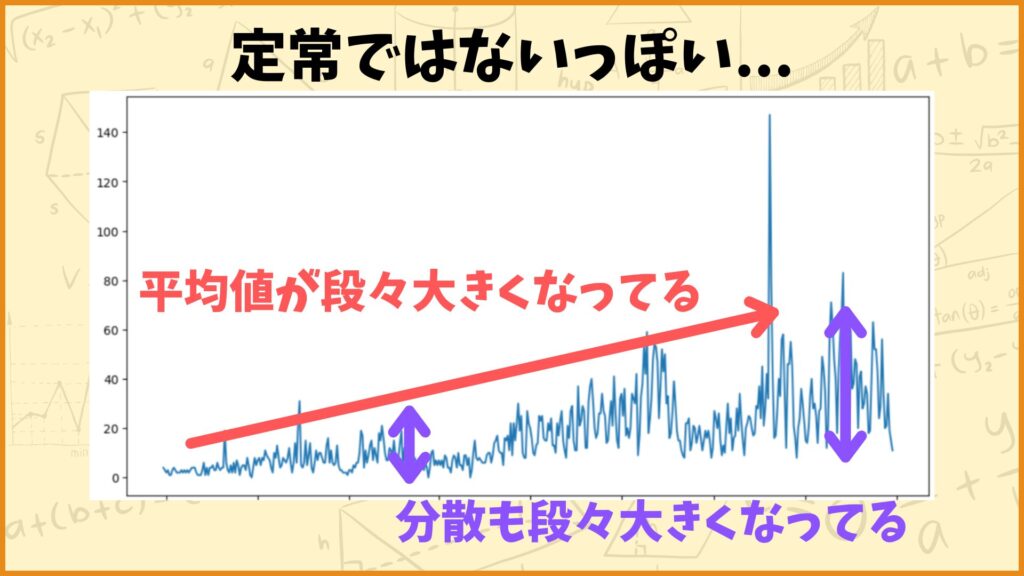
グラフを見ると、データに上昇トレンドがある(平均値が段々大きくなっている)ことが分かります。また昔のデータに比べてデータのぶれ幅も大きくなっている(分散も段々大きくなっている)ことも分かります。
こういうときは1次階差系列(前のデータ値との差を取ったもの)を見てみましょう。この方法は非定常なデータを定常化する処理方法の1つです。
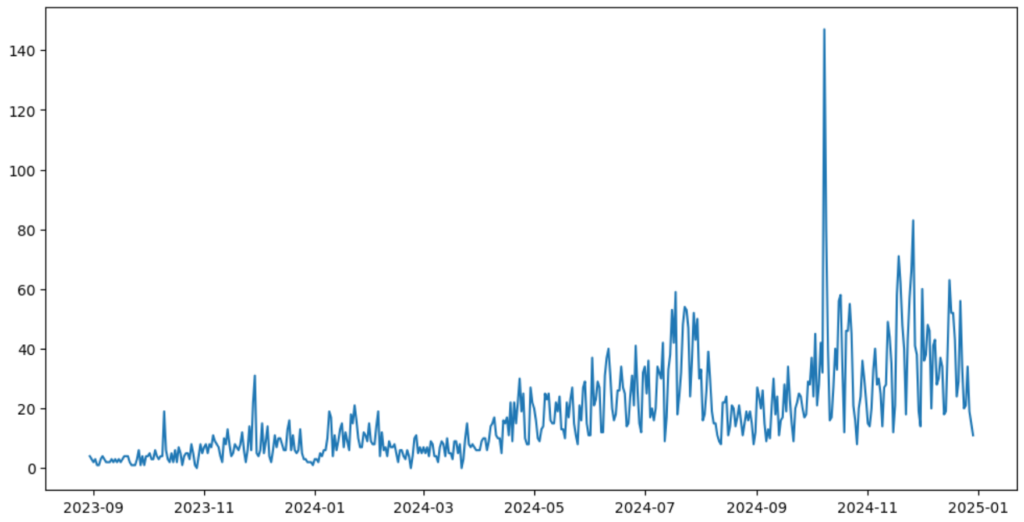
plt.figure(figsize = (12,6))
plt.plot(df["クリック数"])
plt.show()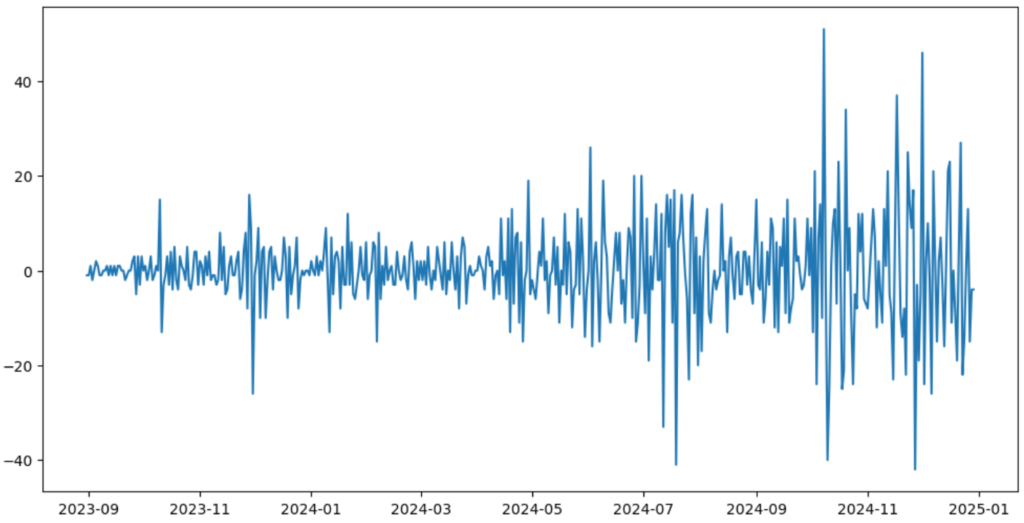
data_diff = df["クリック数"].diff().dropna()
plt.figure(figsize = (12,6))
plt.plot(data_diff)
plt.show()ADF検定を実施して定常性を調べる
グラフを見て定常か非定常か調べるだけでなく、検定も実施して定常性を確かめてみます。ということでADF検定を行ってみましょう。
ADF検定ってなに?
単位根検定の一種。
帰無仮説(H₀):時系列データは単位根を持つ(=非定常)
対立仮説(H₁):時系列データは単位根を持たない(=定常)
p値が有意水準(例えば0.05)を下回るとき帰無仮説を棄却し、データは定常であると判断する。
pythonではstatsmodelsのadfullerを使ってADF検定を実施することができます。今回は有意水準5%で検定します。
原系列に対してADF検定を実施
## 原系列に対してADF検定を実施する
# 事前準備
from statsmodels.tsa.stattools import adfuller
# データの選択
data = df["クリック数"] # 検定したいカラム
# ADF検定
adf_result = adfuller(data)
print("ADF Test:")
print(f"Test Statistic: {adf_result[0]}")
print(f"P-value: {adf_result[1]}")
1次階差系列に対してADF検定を実施
## 1次階差系列に対してADF検定を実施する
# 事前準備
from statsmodels.tsa.stattools import adfuller
# データの選択
data_diff = data.diff().dropna() # 1階階差系列
# ADF検定
adf_result = adfuller(data_diff)
print("ADF Test:")
print(f"Test Statistic: {adf_result[0]}")
print(f"P-value: {adf_result[1]}")
結果を見ると原系列の方はp値が0.14なので帰無仮説を棄却できませんでした。一方1次階差系列の方はp値が\(1.16\times 10^{-6}\)なので帰無仮説を棄却します。
ということで、今回のデータは
原系列が非定常だが、1次階差系列は定常である
と判断したいと思います。
この分析から分かること:
原系列が非定常だが、1次階差系列は定常である
金土はあまりクリックされない…?
自己相関の話をした際に、このデータは7日周期ということが分かりました。ということで各曜日でクリック数に違いがあるのかを調べてみたいと思います。
# 必要なライブラリをインポート
import matplotlib.pyplot as plt
# 曜日の情報を追加する
df["曜日"] = df.index.dayofweek
# 曜日ごとのデータを集計
weekly_data = df.groupby("曜日")["クリック数"].apply(list)
# 箱ひげ図をプロット
plt.figure(figsize=(10, 6))
plt.boxplot(weekly_data, labels=["Mon", "Tue", "Wed", "Thu", "Fri", "Sat", "Sun"])
plt.title("Distribution of data by day of the week")
plt.xlabel("Week")
plt.ylabel("the number of clicks")
plt.grid(axis="y")
plt.show()
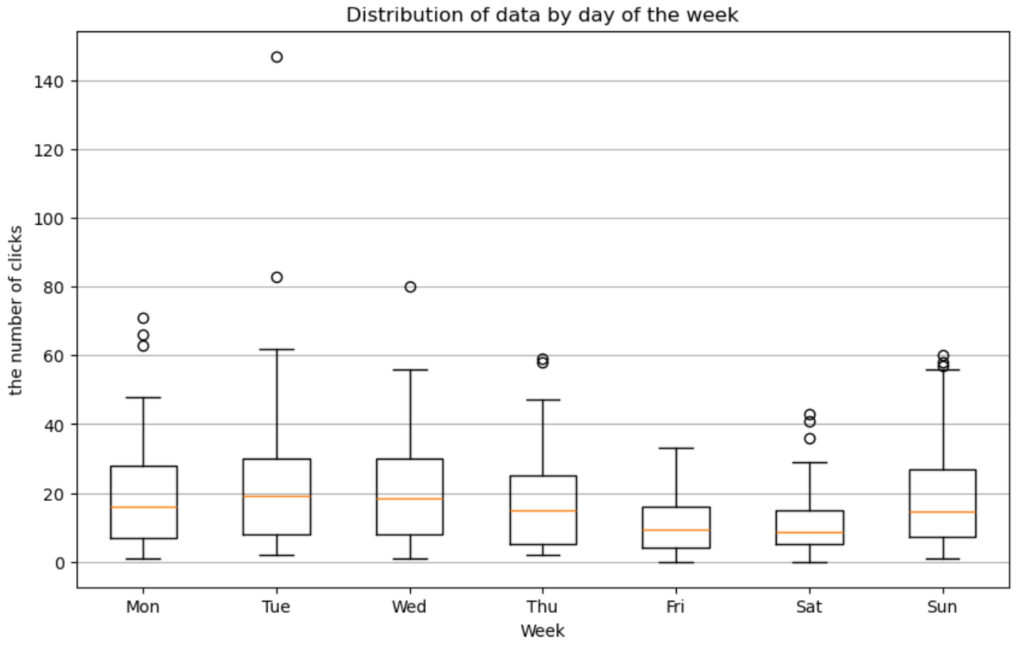
これを見ると、金曜日と土曜日のクリック数が少ない傾向にあるということが分かります。この情報は外生変数としてSARIMAXに組み込めそうです。
この分析から分かること:
金曜日と土曜日はクリック数が少ない傾向がある
なぜ金曜と土曜はクリック数が少ないのかを考えてみました。ぼくが書いている記事は理系大学生向けの勉強、技術記事がメインなので、大学生がよく見ているんだと思います。
とすると金曜と土曜はみんな勉強のやる気がないからあまりクリックされないんじゃないかな~と推測しています。
大学が休みだとあまりクリックされない…?
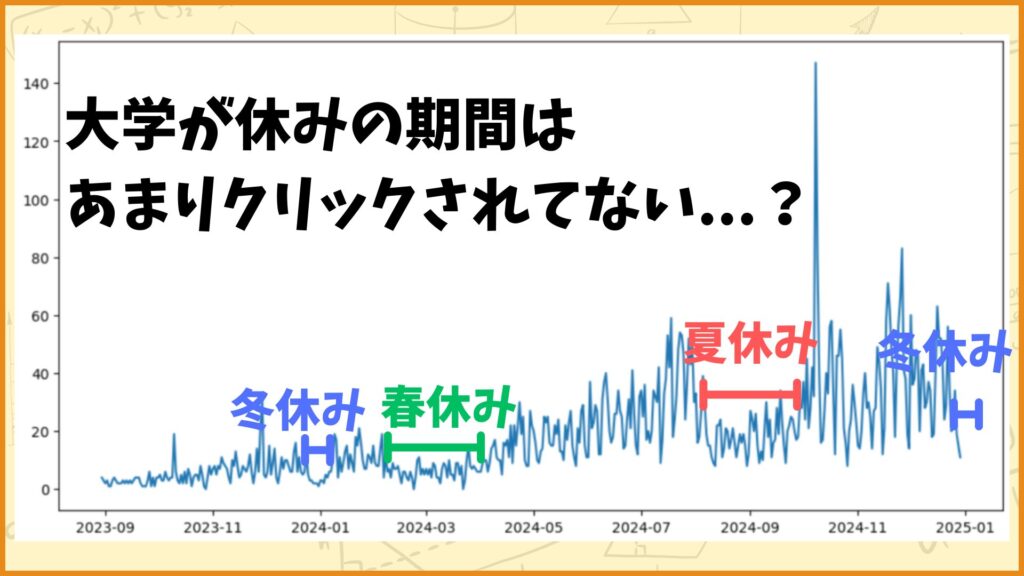
グラフを見ると、大学が休みの期間はあまりクリックされていないように思えます。ということでこれも箱ひげ図を使って調べてみようと思います。休みの期間とその前後の期間を比べて差があるか見てみます。
import pandas as pd
import matplotlib.pyplot as plt
# 大学休み期間の設定
df["大学休み"] = 0
df.loc["2024-02-01":"2024-03-31", "大学休み"] = 1 # 春休み
df.loc["2024-08-01":"2024-09-30", "大学休み"] = 1 # 夏休み
df.loc["2023-12-25":"2024-01-05", "大学休み"] = 1 # 冬休み
df.loc["2024-12-25":"2024-12-29", "大学休み"] = 1 # 冬休み
# 比較用に月別データを抽出
df["month"] = df.index.month
comparison_data = df[(df.index >= "2023-12-20") & (df.index <= "2024-01-10")] # 冬休みの期間とその前後を比べる
comparison_data["period"] = "Non Vacation"
comparison_data.loc["2023-12-25":"2024-01-05", "period"] = "Vacation"
# 箱ひげ図の作成
plt.figure(figsize=(8, 6))
comparison_data.boxplot(column="クリック数", by="period", grid=False)
plt.title("Comparison of Clicks: Vacation vs Non-Vacation (Winter Vacation)")
plt.suptitle("") # 不要なタイトルを削除
plt.xlabel("Period")
plt.ylabel("Clicks")
plt.show()
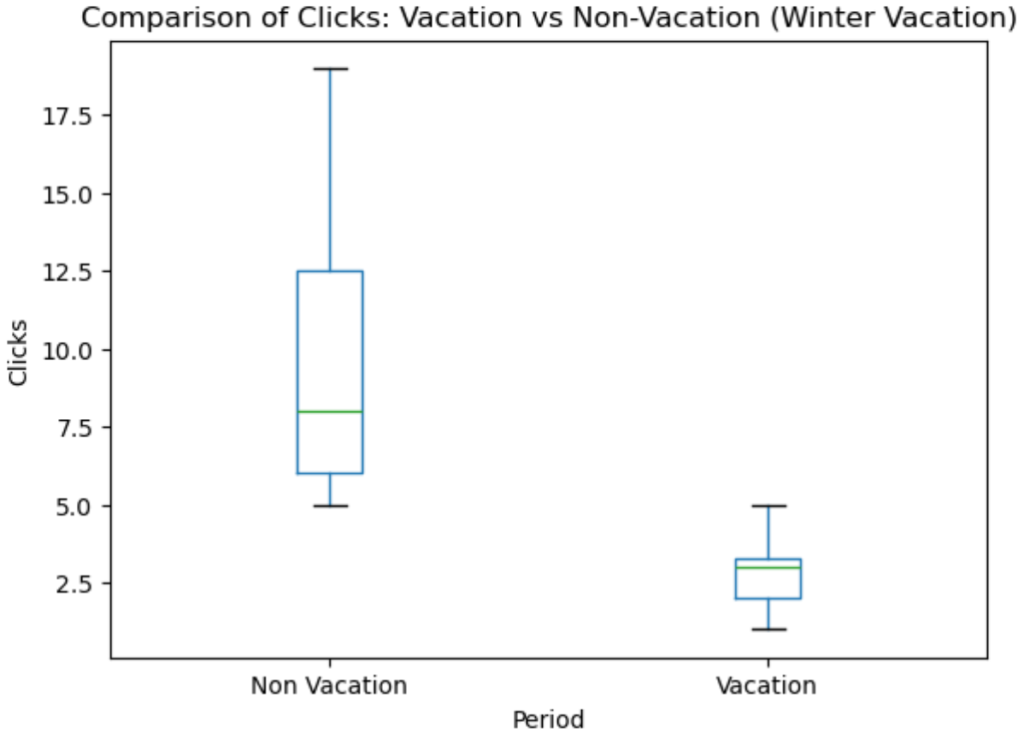
上のグラフは
Vacation : 2023年12月25日~2024年1月5日(冬休みの期間)
Non Vacation :2023年12月20日~2023年12月24日&2024年1月6日~2024年1月10日
でクリック数の分布を比較した箱ひげ図です。これを見ると明らかな差がありますね。冬休み期間中はクリック数が少ないことが分かります。同じように他の休み期間も調べてみましょう。
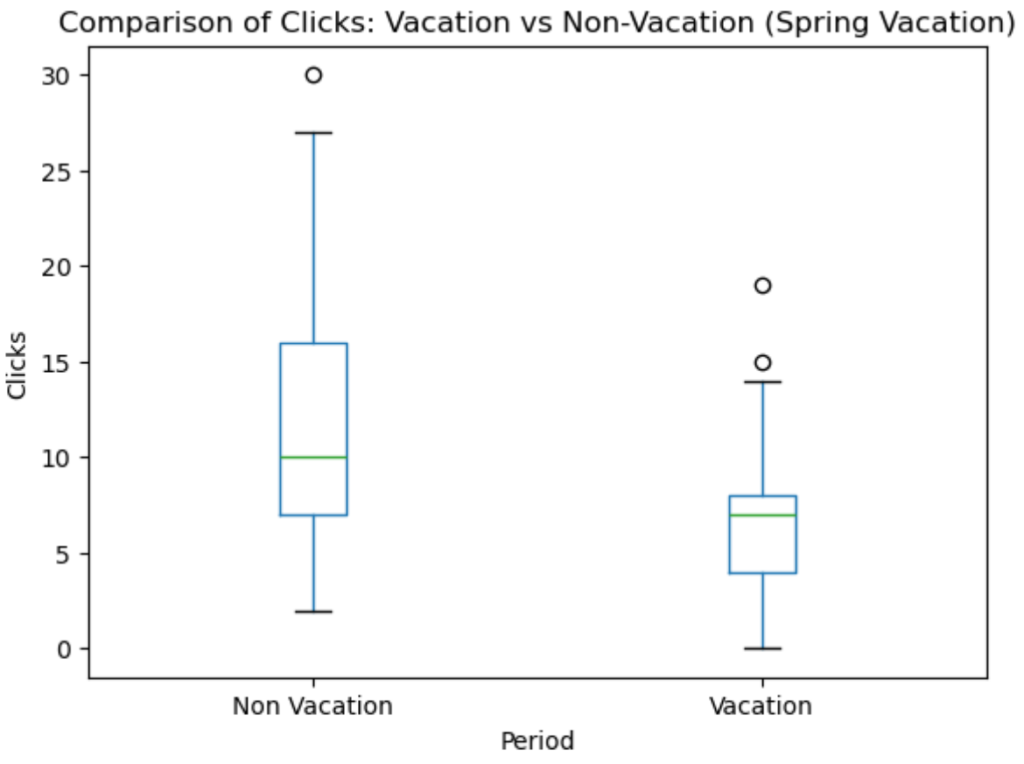
# 比較用に月別データを抽出
df["month"] = df.index.month
comparison_data = df[(df.index >= "2024-01-01") & (df.index <= "2024-04-30")]
comparison_data["period"] = "Non Vacation"
comparison_data.loc["2024-02-01":"2024-03-31", "period"] = "Vacation"
# 箱ひげ図の作成
plt.figure(figsize=(8, 6))
comparison_data.boxplot(column="クリック数", by="period", grid=False)
plt.title("Comparison of Clicks: Vacation vs Non-Vacation (Spring Vacation)")
plt.suptitle("") # 不要なタイトルを削除
plt.xlabel("Period")
plt.ylabel("Clicks")
plt.show()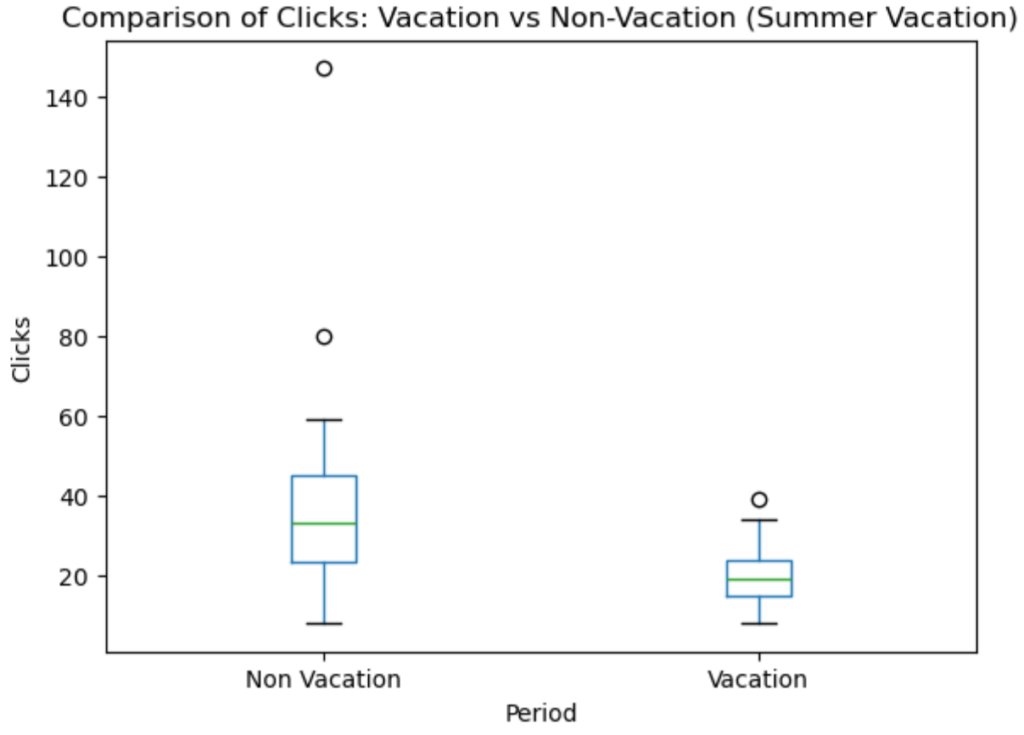
# 比較用に月別データを抽出
df["month"] = df.index.month
comparison_data = df[(df.index >= "2023-12-20") & (df.index <= "2024-01-10")]
comparison_data["period"] = "Non Vacation"
comparison_data.loc["2023-12-25":"2024-01-05", "period"] = "Vacation"
# 箱ひげ図の作成
plt.figure(figsize=(8, 6))
comparison_data.boxplot(column="クリック数", by="period", grid=False)
plt.title("Comparison of Clicks: Vacation vs Non-Vacation (Winter Vacation)")
plt.suptitle("") # 不要なタイトルを削除
plt.xlabel("Period")
plt.ylabel("Clicks")
plt.show()
上の2つのグラフを見ると、春休みも夏休みの期間もクリック数が少ないことが分かりますね。ということで大学が休みの期間はあまりクリックされないと判断しても良さそうです。これもSARIMAXの外生変数として組み込めそうです。
この分析から分かること:
大学が休みの期間はクリック数が少ない傾向がある
このようになる理由も1つ前の話と同じで、大学が休みの期間は皆勉強しないからだと思います。
本当は検定を行って差があることを確かめるべきなんだと思いますが、自分の勉強不足で、今回のような時系列データに対してそのまま検定(t検定とかマンホイットニーのU検定とか)を実施して良いのか分かんなかったので、箱ひげ図での比較にしました。詳しい方がいたら教えていただけるとありがたいです😢
外生変数って何が考えられる?
これまでの議論から以下の2つの特徴が分かりました。
金土はクリック数が少ない
大学が休みの期間はクリック数が少ない
これらを外生変数としてSARIMAXに追加したいと思います。
金曜日or土曜日なら1、それ以外なら0を取る変数
大学が休みの期間なら1、そうでないなら0を取る変数
# 曜日の情報を追加する
df["曜日"] = df.index.dayofweek
# 金曜日または土曜日を判定するダミー変数を作成
df["金土"] = df["曜日"].isin([4, 5]).astype(int)# 大学の休み期間の設定
df["大学休み"] = 0
df.loc["2024-02-01":"2024-03-31", "大学休み"] = 1
df.loc["2024-08-01":"2024-09-30", "大学休み"] = 1
df.loc["2023-12-25":"2024-01-05", "大学休み"] = 1
df.loc["2024-12-25":"2024-12-29", "大学休み"] = 1
外生変数が用意できたので、この「曜日」列と「大学休み」列をSARIMAXに突っ込んでみます。
SARIMAXで予測する
それでは実際にSARIMAXで予測をしていきましょう。
訓練データとテストデータに分ける
それではまずデータを訓練データとテストデータに分けましょう。今回は
訓練データ:2023年8月30日~2024年10月31日
テストデータその1:2024年11月1日~2024年11月30日
テストデータその2:2024年12月1日~2024年12月29日
としたいと思います。
# Train, Test の分割
train_data = df.loc[:"2024-10-31"].copy()
test_data_11 = df.loc["2024-11-01":"2024-11-30"].copy()
test_data_12 = df.loc["2024-12-01":"2024-12-29"].copy()パラメータチューニングをする!
パラメータチューニングはこちらの記事を参考にして行いました。
考えられるパラメータの組合せを全列挙し、グリッドサーチによって最適なパラメータを求めます。なおこれまでの議論から周期は7日間として、残りの6つのパラメータをチューニングしていきます。
# 考えられるパラメータの組み合わせを全て作成
max_p = 2
max_q = 2
max_d = 2
max_sp = 1
max_sd = 1
max_sq = 1
params = []
for p in range(0, max_p + 1):
for q in range(0, max_q + 1):
for d in range(0, max_d + 1):
for sp in range(0, max_sp + 1):
for sd in range(0, max_sd + 1):
for sq in range(0, max_sq + 1):
params.append([p,d,q,sp,sd,sq])評価指標はAIC(赤池情報量規準)で、これが最小となるパラメータを選びます。なお最適化プロセスにおいて収束しないなどのwarningが出たパラメータの組合せはスキップして、warningが出なかったものだけを対象にしています。
import warnings
from statsmodels.tsa.statespace.sarimax import SARIMAX
# ベストパラメータの初期化
best_param = None
best_param_seasonal = None
best_aic = float("inf")
# 警告をキャッチするためのリスト
excluded_params = []
# パラメータループ
for param in params:
try:
with warnings.catch_warnings(record=True) as w:
# 警告を一時的にキャッチ
warnings.simplefilter("always")
# SARIMAモデルを構築
model = SARIMAX(
train_data["クリック数"],
order=(param[0], param[1], param[2]),
seasonal_order=(param[3], param[4], param[5], 7),
exog=train_data[["大学休み", "金土"]]
)
results = model.fit(disp=False)
# 警告が発生したか確認
if any("Non-stationary" in str(warn.message) or "Non-invertible" in str(warn.message) or "failed to converge" in str(warn.message) for warn in w):
print(f"Excluded ARIMA{(param[0], param[1], param[2])}x{(param[3], param[4], param[5], 7)} due to warnings.")
excluded_params.append(param)
continue # このパラメータをスキップ
# AICを比較してベストパラメータを更新
print("SARIMAX{}x{}7 - AIC:{}".format((param[0], param[1], param[2]), (param[3], param[4], param[5], 7), results.aic))
if best_aic > results.aic:
best_param = (param[0], param[1], param[2])
best_param_seasonal = (param[3], param[4], param[5], 7)
best_aic = results.aic
except Exception as e:
print(f"Failed for SARIMAX{(param[0], param[1], param[2])}x{(param[3], param[4], param[5], 7)}: {e}")
continue # エラーが発生した場合も次のパラメータに進む
# ベストパラメータの結果を表示
print(f"BEST SARIMAX{best_param}x{best_param_seasonal}7 - AIC:{best_aic}")
if excluded_params:
print(f"Excluded parameters: {excluded_params}")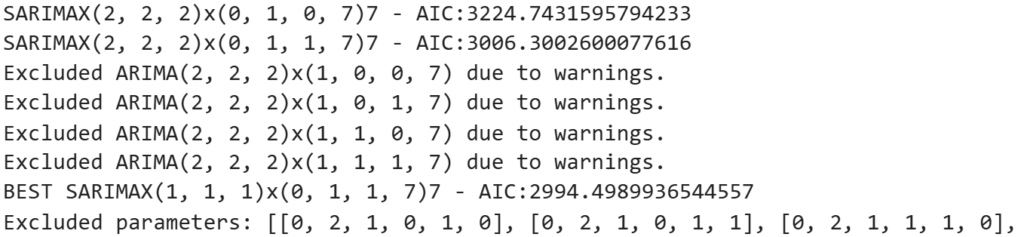
ということで最適なパラメータが
SARIMAX(1, 1, 1)x(0, 1, 1, 7)
と決まりました。
予測結果を見てみる!
それでは先ほど求めたパラメータを代入してSARIMAXを動かしてみます。まずは11月のデータを予測してみようと思います。予測方法はロールフォワード法というものを使おうと思います。
ロールフォワード法:
1期先を予測し、その観測値を訓練データに含めて再度モデルを学習・予測するというプロセスを繰り返す。
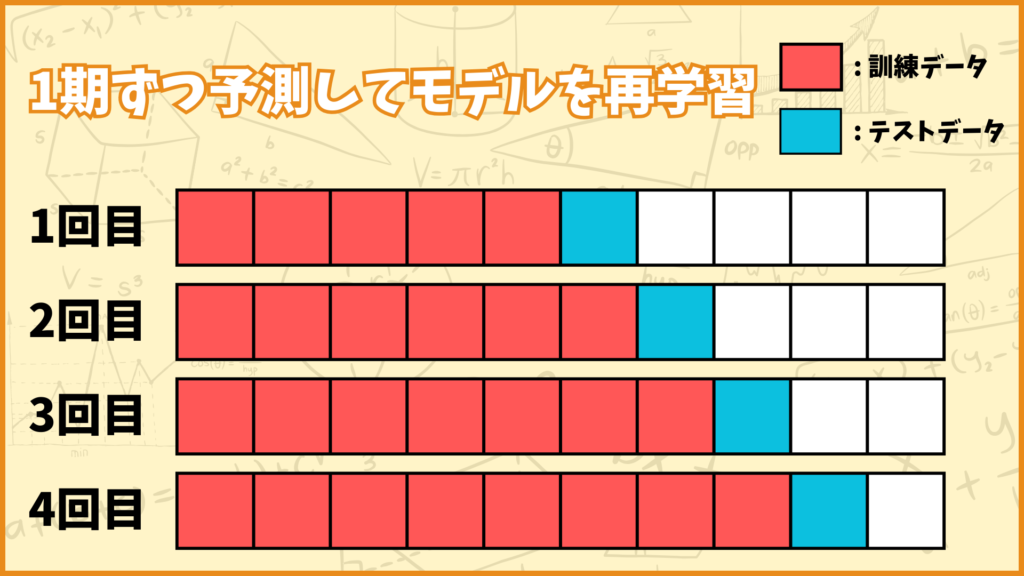
今回は11月1日~11月30日の30期間の予測をするので30回予測をします。
import pandas as pd
import numpy as np
import matplotlib.pyplot as plt
from statsmodels.tsa.statespace.sarimax import SARIMAX
from sklearn.metrics import mean_absolute_percentage_error
# 11月
test_data = test_data_11
# 予測結果と実際の値を格納するリスト
predictions = []
actuals = []
# 学習データをコピーしてローリングに使用
history = train_data.copy()
# テストデータを1日ずつ予測
for date in test_data.index:
# SARIMAモデルの再構築・再学習
model = SARIMAX(
history["クリック数"],
order=(1, 1, 1),
seasonal_order=(0, 1, 1, 7),
exog=history[["大学休み", "金土"]]
)
model_fit = model.fit(disp=False)
# テストデータの1日分を予測
exog_test = test_data.loc[[date], ["大学休み", "金土"]]
forecast = model_fit.get_forecast(steps=1, exog=exog_test)
prediction = forecast.predicted_mean.iloc[0]
# 予測値と実際値を記録
predictions.append(prediction)
actuals.append(test_data.loc[date, "クリック数"])
# 実測値を履歴(学習データ)に追加
new_row = test_data.loc[[date], ["クリック数", "大学休み", "金土"]]
history = pd.concat([history, new_row])
# 結果をデータフレームにまとめる
results = pd.DataFrame({
"Actual": actuals,
"Prediction": predictions
}, index=test_data.index)# 結果のプロット
plt.figure(figsize=(20, 6))
plt.plot(results.index, results["Actual"], label="Actual", color="blue")
plt.plot(results.index, results["Prediction"], label="Prediction", color="red")
plt.title("Rolling Forecast with SARIMAX")
plt.legend()
plt.xlabel("Date")
plt.ylabel("Click Counts")
plt.grid()
plt.show()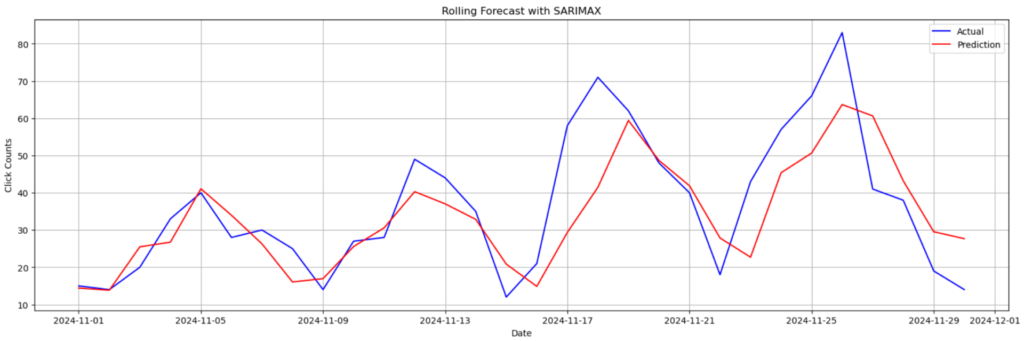
これを見ると、周期性は再現できており、11月前半はかなり良い精度で予測できていますが、11月後半は結構予測にずれがありますね。
# MAPEの計算
mape_first = mean_absolute_percentage_error(results["2024-11-01":"2024-11-15"]["Actual"], results["2024-11-01":"2024-11-15"]["Prediction"])
mape_last = mean_absolute_percentage_error(results["2024-11-16":"2024-11-30"]["Actual"], results["2024-11-16":"2024-11-30"]["Prediction"])
mape_all = mean_absolute_percentage_error(results["Actual"], results["Prediction"])
print(f"MAPE(11月1日~11月15日): {mape_first:.2%}")
print(f"MAPE(11月16日~11月30日): {mape_last:.2%}")
print(f"MAPE(11月全体): {mape_all:.2%}")
MAPEを見ても、やっぱり11月後半はあまり予測精度が高くないですね。11月後半の実データを見ると上下の変動が激しく、モデルはそれを上手く反映できていないですね。
ただ11月前半は割と上手に予測できているようで良かったです(⌒∇⌒)
12月のデータも予測したらダメダメだった…
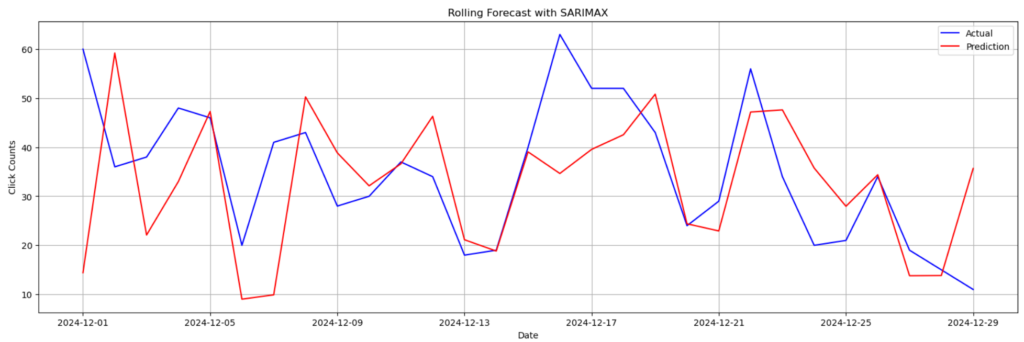

12月のデータを使って予測をしてみましたが、上図の通り結果はダメダメでした😢
対数変換をして同じように予測してみましたが、それもあまりうまくいきませんでした。うまくいかなかった理由の1つとして、周期性が12月はあまり見られないというのがあるのかなと思いました。
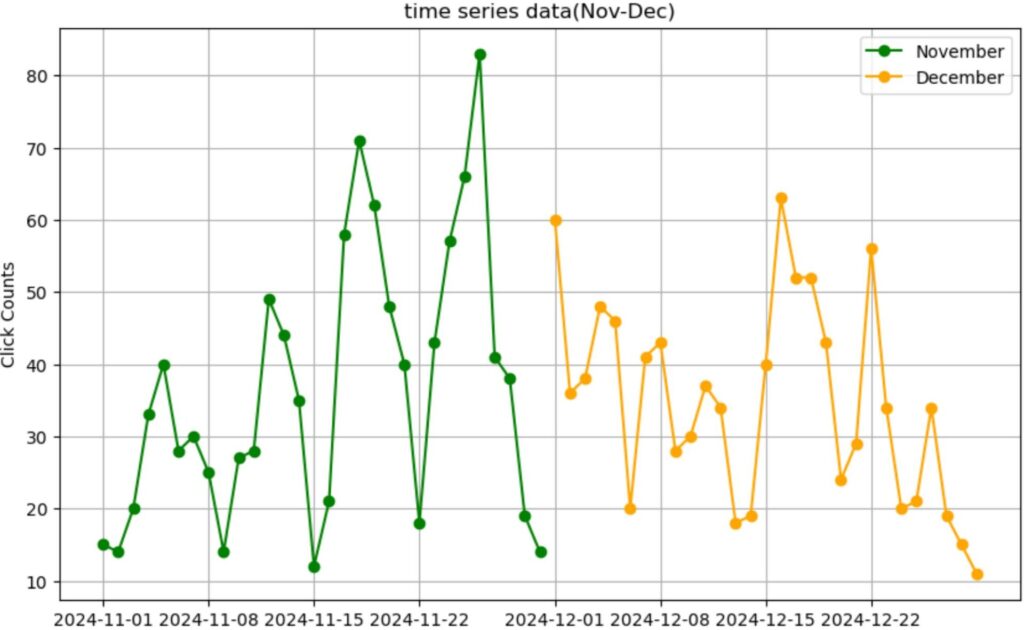
11月はだいたい7日周期で山がありますが、12月はその傾向が無くなっているっぽいです。なぜ12月は周期性が無くなったのかは分かりませんが、外生変数として新たに追加すべき要素があるのかもしれません。
また他にも1次階差系列はADF検定により定常であると判断しましたが、分散が段々大きくなっているような気がします。11月の予測も後半は分散が大きくなっているのを上手く反映できていないように感じます。これも対処した方が良いのかなと思いました。
それ以外にもきっとたくさん改善点があると思うので、引き続き時系列データについて勉強していきたいと思います。
おわりに
いかがでしたか。
今回の記事ではSARIMAXを使ってみました。
今後もこのようなデータ分析に関する記事を書いていきます!
最後までこの記事を読んでくれてありがとうございました。



