- 短時間で質の良い解がほしい…
- 焼きなまし法を使って良い解を求めたい…
- 制約が多い最適化問題を解きたい…
こんにちは!しゅんです!
今回の記事では制約が多い最適化問題に対して焼きなまし法を適用したらどうなるかを実験してみたいと思います!
それではやっていきましょう!
普段は組合せ最適化の記事を書いてたりします。
ぜひ他の記事も読んでみてください!
このブログの簡単な紹介はこちらに書いてあります。
興味があったら見てみてください。
このブログでは経営工学を勉強している現役理系大学生が、経営工学に関することを色々話していきます!
ぼくが経営工学を勉強している中で感じたことや、興味深かったことを皆さんと共有出来たら良いなと思っています。
そもそも経営工学とは何なのでしょうか。Wikipediaによると
経営工学(けいえいこうがく、英: engineering management)は、人・材料・装置・情報・エネルギーを総合したシステムの設計・改善・確立に関する活動である。そのシステムから得られる結果を明示し、予測し、評価するために、工学的な分析・設計の原理・方法とともに、数学、物理および社会科学の専門知識と経験を利用する。
引用元 : 経営工学 – Wikipedia
長々と書いてありますが、要は経営、経済の課題を理系的な観点から解決する学問です。
今回扱う問題(シフトスケジューリング問題)
詳しい話は過去の記事で解説しているので、ここではザックリと紹介したいと思います。
シフトスケジューリング問題ってなに?
今回はシフトスケジューリング問題を焼きなまし法を使って解きたいと思います。シフトスケジューリング問題は、多くの企業や組織で直面する代表的な組合せ最適化問題です。
しかしシフトスケジューリング問題を解こうとすると、結構制約が多かったりします。例えば下記のような制約が挙げられます。
- 複数の従業員がいて、それぞれ働ける曜日・時間帯が違う
- 労働時間に上限がある
- 勤務日数や連続勤務に制限がある
- 勤務回数の公平性を考慮したい
- 休憩時間の確保、法定休日の確保…
こうした多岐にわたる制約を考慮しつつ、人員配置(シフト表)を決めなければなりません。
本記事で扱うシフトスケジューリング問題
シフトスケジューリング問題には本当に様々なバリエーションがありますが、ここでは以下のように設定してみます。
期間:
1カ月(28日間)のシフトを決める。
スタッフ:
10人いる。
シフト枠:
各日「早番」「日勤」「遅番」の3シフト、計84シフト(28日×3)。
要件:
各シフトには必ず1人配置しなければならない。
1人のスタッフが1日に2シフト入ることはない(早番、日勤、遅番の掛け持ち不可)。
各スタッフの総勤務回数は最大10回まで。
スタッフによっては「出勤不可日」がある(たとえば従業員1は土日NGなど)。
なるべく全員の勤務回数が偏らないようにしたい(公平性)。
上記を満たしつつ、なるべくバランスよく配置を決めることが目標です。
シフト候補は組合せが膨大になるうえ、「必須制約 + 希望制約(優先度)」が入り乱れるため、すべてを厳密に解こうとすると計算量が爆発しがちです。
ということで焼きなまし法を使ってこの問題を解こうと思います。
焼きなまし法ってなに?
焼きなまし法の大まかな流れ
焼きなまし法 (Simulated Annealing) の大まかな流れは以下の通りです。
1.初期解を用意:
シフト表を何らかの方法で1つ作る(例:完全ランダム)
2.近傍解を生成:
既存のシフト表を少しだけ変更して別のシフト表を作る
3.評価関数(コスト)の計算:
コストが小さい方が良い
シフト表が満たしている or 破っている制約を評価し、数値に落とし込む
4.受理判定:
既存の解よりも良い解(コストが低い→良い)なら必ず受け入れる
悪い解も確率的に受け入れる(温度パラメータに依存)
5.温度を下げる:
探索を続けながら徐々に温度を下げ、悪い解を受け入れにくくする
6.繰り返し:
一定回数あるいは収束するまで続ける
焼きなまし法は過去の記事でも解説しています。詳細な解説はそちらでしているのでぜひそちらの記事も見てみてください!
\\ 過去の記事はこちらから! //
この記事のメインは
「制約条件がたくさんある問題だとどうすれば良いか」
ということです。制約が多い問題では「評価関数をどう作るか」「無効なシフト表をどう扱うか」が大きな課題となります。
制約条件が多いときの焼きなまし法の実装方法
今回は下記の3つの方法を試してみます。どれもよく使われる手法ですが、それぞれメリット・デメリットがあります。
手法1:評価関数にペナルティを追加する方法
概要:
評価関数(コスト)に「制約違反の度合い」をペナルティとして加算し、違反が多いほどコストを大きくする。
メリット:
実装がシンプル。制約を一元的に「ペナルティ」として扱える。
デメリット:
ペナルティの重み付けが難しい。大きすぎると制約違反解がほぼ受け入れられず行き詰まる、小さすぎると制約を無視しがちになる、など。
手法2:制約違反がある近傍解は最初から生成しない
概要:
近傍を生成した際に制約違反となるようなシフト表は「なかったこと」にして、もう一度近傍を作り直す。
(例:Aさんが土日は出勤不可なのに、土曜遅番にAを割り当てたら、その割り当てを無効にしてもう一度近傍解を生成する。)
メリット:
コスト関数を「有効解のみを評価する」シンプルな形にできる。
デメリット:
制約が多い場合、近傍自体を生成しにくくなる可能性があり、探索効率が下がる。
手法3:制約違反がある近傍解を修復する
概要:
一旦制約を気にせず近傍を作り、違反があれば修復ルーチンで直す。
(例:週4回を超えて勤務が割り当てられた人がいたら、まだ週2回の別の人にシフトを回す。)
メリット:
多様な解を探索しつつ、最終的には制約を満たすシフト表に変換できる。
デメリット:
修復ロジックを設計するのが大変。修復で別の制約を破ってしまう場合もあり、複雑になりがち。
pythonで実装する
それではpythonで実装してみましょう。それぞれの方法を個別に試すため、評価関数と近傍生成まわりの実装を3パターン用意します。
共通の設定
import random
import math
# ---- シフトスケジューリングの共通情報 ----
# 4週間(28日)
days = [f"Day{i+1}" for i in range(28)]
# 1日3シフト(例:早番・日勤・遅番)
shifts_per_day = 3
# 全シフト数 = 28日 × 3シフト = 84
NUM_SHIFTS = len(days) * shifts_per_day
# スタッフ10人 (名前を文字列で管理)
staff = [f"Staff{i}" for i in range(10)]
# 出勤不可日の例(辞書で管理)
unavailable = {
"Staff0": ["Day2", "Day4", "Day9", "Day21"],
"Staff1": ["Day6", "Day7", "Day12", "Day22", "Day28"],
"Staff2": ["Day5", "Day8", "Day15", "Day16"],
"Staff3": ["Day1", "Day3", "Day9", "Day20", "Day25"],
"Staff4": ["Day7", "Day19", "Day23", "Day26"],
"Staff5": ["Day1", "Day13", "Day18"],
"Staff6": ["Day11", "Day14", "Day17", "Day21"],
"Staff7": ["Day4", "Day16", "Day18", "Day19", "Day25", "Day27"],
"Staff8": ["Day2", "Day6", "Day10", "Day15", "Day20", "Day28"],
"Staff9": ["Day4", "Day12", "Day15", "Day21", "Day28"]
}
# 週の最大勤務回数 → 今回は1ヶ月スパンなので、単純に "全期間で10回まで" など
# (28日×3シフト=84枠を10人で回すと1人あたり平均8〜9回のイメージ)
max_shifts_per_person = 10
def create_initial_solution():
"""
ランダムにシフト表を作成。
解の表現としては、シフト枠の長さ84に対して、staffのインデックスを割り当てたリストを想定。
例) [0, 1, 2, 0, ...]
"""
solution = []
for i in range(NUM_SHIFTS):
solution.append(random.randint(0, len(staff) - 1))
return solution
ここまでは、どの手法でも共通です。「解」は「長さ84のリスト」で、各要素にスタッフのインデックスが入る形とします。
手法1の実装
評価関数
def cost_function_penalty(solution):
"""
ペナルティ法: シンプルに
- '勤務回数の偏り' をベースコストに
- そこに '制約違反のペナルティ' を加算
"""
# ベースコスト: (スタッフごとの勤務回数の標準偏差) を小さくしたいと仮定
# 例: 均等に分担できるほど良い → 分散が小さいほど良い
count_per_staff = [0] * len(staff)
for shift_idx, s_idx in enumerate(solution):
count_per_staff[s_idx] += 1
base_cost = calc_std_dev(count_per_staff) # 標準偏差を計算
# 制約違反ペナルティ
penalty = 0
# (1) max_shifts_per_person = 10 を超える人がいたらペナルティ
for c in count_per_staff:
if c > max_shifts_per_person:
penalty += (c - max_shifts_per_person) * 10
# (2) 出勤不可日を破っていないか
for shift_idx, s_idx in enumerate(solution):
staff_name = staff[s_idx]
day_idx = shift_idx // shifts_per_day
day_name = days[day_idx]
if staff_name in unavailable:
if day_name in unavailable[staff_name]:
penalty += 20
# (3) 1日に同じスタッフが2シフト入ってるか?
# 今回は penalty function でなくすごくシンプルに
day_assignments = {}
for i in range(len(days)):
day_assignments[i] = []
for shift_idx, s_idx in enumerate(solution):
day_idx = shift_idx // shifts_per_day
day_assignments[day_idx].append(s_idx)
for d in day_assignments:
if len(set(day_assignments[d])) < len(day_assignments[d]):
# もし同じスタッフが同日の2シフトに入っていたら
penalty += 50 # 重めに設定
return base_cost + penalty
def calc_std_dev(values):
"""
標準偏差を計算する簡易関数(勤務回数の偏りを評価する関数)
"""
import statistics
if len(values) <= 1:
return 0
return statistics.pstdev(values) # population stdev
従業員間の勤務回数の偏りは標準偏差で測りたいと思います。MIPソルバーで解くわけじゃないので、非線形な関数を扱うこともできますね。
近傍解生成
def generate_neighbor(solution):
"""
近傍生成:ランダムに1つのシフト枠を選び、担当をランダムに変更
"""
new_solution = solution[:]
idx = random.randint(0, NUM_SHIFTS - 1)
new_solution[idx] = random.randint(0, len(staff) - 1)
return new_solution
近傍解をランダムに生成しています。
焼きなまし法の実装
def simulated_annealing_penalty(max_iter=1000, initial_temp=100.0, cooling_rate=0.99):
current_sol = create_initial_solution()
current_cost = cost_function_penalty(current_sol)
best_sol = current_sol[:]
best_cost = current_cost
temp = initial_temp
for i in range(max_iter):
neighbor = generate_neighbor(current_sol)
neighbor_cost = cost_function_penalty(neighbor)
delta = neighbor_cost - current_cost
if delta < 0:
# 良い解なら受け入れ
current_sol = neighbor
current_cost = neighbor_cost
else:
# 悪い解も一定確率で受け入れ
if random.random() < math.exp(-delta / temp):
current_sol = neighbor
current_cost = neighbor_cost
# ベスト更新
if current_cost < best_cost:
best_sol = current_sol[:]
best_cost = current_cost
# 温度を下げる
temp *= cooling_rate
return best_sol, best_cost手法2の実装
「制約を破る解」を作ってしまったら捨てる、という方針です。この場合、評価関数は「有効解の評価」だけでOKとなります。
評価関数
ペナルティを考えなくていいので、「均等度」だけを評価します。
def cost_function_valid_only(solution):
"""
有効解(制約を満たす)の場合のみ評価する。
無効解だったら「+∞」を返す(実質的に使われない想定)。
"""
if not is_valid_solution(solution):
return float("inf") # 無効解には極大のコストを与える
# 有効解の場合:スタッフごとの勤務回数の標準偏差
count_per_staff = [0] * len(staff)
for s_idx in solution:
count_per_staff[s_idx] += 1
return calc_std_dev(count_per_staff)
def is_valid_solution(solution):
"""
解がすべての制約を満たしているかを判定
"""
count_per_staff = [0] * len(staff)
day_assignments = [[] for _ in range(len(days))]
for shift_idx, s_idx in enumerate(solution):
# (1) 週4回を超えていないか
count_per_staff[s_idx] += 1
if count_per_staff[s_idx] > max_shifts_per_person:
return False
# (2) 出勤不可日の確認
staff_name = staff[s_idx]
day_idx = shift_idx // shifts_per_day
day_name = days[day_idx]
if staff_name in unavailable and day_name in unavailable[staff_name]:
return False
# (3) 同日に同じスタッフが2シフト入っていないか
day_assignments[day_idx].append(s_idx)
for d in range(len(days)):
if len(set(day_assignments[d])) < len(day_assignments[d]):
return False
return True
近傍生成
ここでの肝は、「無効解が出たら再生成する」仕組みを入れること。以下のようにして「制限回数リトライ」してみる、などの方法があります。
def generate_neighbor_valid(solution, max_attempts=100):
"""
近傍解を生成するが、もし無効解なら再生成する。
max_attempts 回まで試してダメなら仕方なくそのまま返す(ペナルティ扱いに近い)
"""
for _ in range(max_attempts):
new_solution = solution[:]
idx = random.randint(0, NUM_SHIFTS - 1)
new_solution[idx] = random.randint(0, len(staff) - 1)
if is_valid_solution(new_solution):
return new_solution
# もしmax_attempts回再生成してもダメなら諦めて返す
return new_solution # たとえ無効でもとりあえず返す焼きなまし法の実装
def simulated_annealing_valid_only(max_iter=1000, initial_temp=100.0, cooling_rate=0.99):
current_sol = create_initial_solution()
# 初期解が無効の可能性もあるので、有効解になるまで一応再生成してもいい
for _ in range(100):
if is_valid_solution(current_sol):
break
else:
current_sol = create_initial_solution()
current_cost = cost_function_valid_only(current_sol)
best_sol = current_sol[:]
best_cost = current_cost
temp = initial_temp
for i in range(max_iter):
neighbor = generate_neighbor_valid(current_sol)
neighbor_cost = cost_function_valid_only(neighbor)
delta = neighbor_cost - current_cost
if delta < 0:
current_sol = neighbor
current_cost = neighbor_cost
else:
if random.random() < math.exp(-delta / temp):
current_sol = neighbor
current_cost = neighbor_cost
if current_cost < best_cost:
best_sol = current_sol[:]
best_cost = current_cost
temp *= cooling_rate
return best_sol, best_cost
手法3の実装
制約違反の解を生成してしまっても、何とか修正(修復)してから評価する手法です。
評価関数
ペナルティ法同様、修復後の解を評価する形にします。今回は「解を修復してからスタッフの勤務回数の標準偏差を計算」という流れで考えます。
def cost_function_repair(solution):
"""
1) solutionを修復して有効解にする(極力制約違反を取り除く)
2) 修復後の解を評価して返す
"""
repaired = repair_solution(solution)
# 修復した解でスタッフごとの勤務回数の標準偏差をコストとして返す
count_per_staff = [0] * len(staff)
for s_idx in repaired:
count_per_staff[s_idx] += 1
return calc_std_dev(count_per_staff), repaired修復関数
簡易的に以下のようなロジックで違反部分を直すとします。
1. 週4回を超えたスタッフがいれば、週4回以下のスタッフに割り当て直す
2. 出勤不可日を割り当てていたら、他のスタッフに変更
3. 同日の2シフトを同じ人に入れていたら、別のスタッフに割り当て直す
def repair_solution(solution):
new_solution = solution[:]
# スタッフごとの勤務回数をチェック
count_per_staff = [0] * len(staff)
for s_idx in new_solution:
count_per_staff[s_idx] += 1
for shift_idx, s_idx in enumerate(new_solution):
day_idx = shift_idx // shifts_per_day
day_name = days[day_idx]
staff_name = staff[s_idx]
# (1) 勤務回数上限チェック
if count_per_staff[s_idx] > max_shifts_per_person:
# 超過していたら、誰か他のスタッフに割り当て直す
new_s_idx = find_alternative_staff(day_name, count_per_staff)
if new_s_idx is not None:
# カウントの付け替え
count_per_staff[s_idx] -= 1
count_per_staff[new_s_idx] += 1
new_solution[shift_idx] = new_s_idx
s_idx = new_s_idx # 上書き
# (2) 出勤不可日のチェック
if staff_name in unavailable and day_name in unavailable[staff_name]:
# NGなので誰か他のスタッフに振り替え
new_s_idx = find_alternative_staff(day_name, count_per_staff)
if new_s_idx is not None:
count_per_staff[s_idx] -= 1
count_per_staff[new_s_idx] += 1
new_solution[shift_idx] = new_s_idx
s_idx = new_s_idx
# (3) 同日の2シフト割り当てのチェック
day_assignments = [[] for _ in range(len(days))]
for shift_idx, s_idx in enumerate(new_solution):
day_idx = shift_idx // shifts_per_day
day_assignments[day_idx].append((shift_idx, s_idx))
for d_idx, shifts in enumerate(day_assignments):
used_staff = set()
for shift_info in shifts:
s_idx = shift_info[1]
if s_idx in used_staff:
# 同じスタッフがもう使われている!
# 誰か他のスタッフに変更
shift_idx = shift_info[0]
new_s_idx = find_alternative_staff(days[d_idx], count_per_staff)
if new_s_idx is not None:
# カウントの付け替え
count_per_staff[s_idx] -= 1
count_per_staff[new_s_idx] += 1
new_solution[shift_idx] = new_s_idx
used_staff.add(new_s_idx)
else:
# 見つからなかったら仕方ないが、ここでは何もしない(実際はどうにかしたい)
pass
else:
used_staff.add(s_idx)
return new_solution
def find_alternative_staff(day_name, count_per_staff):
"""
day_nameに出勤可能で、まだmax_shifts_per_personに余裕があるスタッフを見つける
"""
candidates = []
for i, st in enumerate(staff):
if st in unavailable and day_name in unavailable[st]:
continue # 出勤不可
if count_per_staff[i] < max_shifts_per_person:
candidates.append(i)
if candidates:
return random.choice(candidates)
return None # いなければNone
焼きなまし方法の実装
評価関数内で修復しているので、近傍生成自体はシンプルなままでOKです。
def simulated_annealing_repair(max_iter=1000, initial_temp=100.0, cooling_rate=0.99):
current_sol = create_initial_solution()
current_cost, current_sol = cost_function_repair(current_sol)
best_sol = current_sol[:]
best_cost = current_cost
temp = initial_temp
for i in range(max_iter):
neighbor = generate_neighbor(current_sol)
neighbor_cost, neighbor = cost_function_repair(neighbor)
delta = neighbor_cost - current_cost
if delta < 0:
current_sol = neighbor
current_cost = neighbor_cost
else:
if random.random() < math.exp(-delta / temp):
current_sol = neighbor
current_cost = neighbor_cost
if current_cost < best_cost:
best_sol = current_sol[:]
best_cost = current_cost
temp *= cooling_rate
return best_sol, best_cost実験結果・比較
手法1の出力解:
・制約違反:なし
・最大出勤日数:9日
・最小出勤日数:8日
手法2の出力解:
・制約違反:あり
手法3の出力解:
・制約違反:なし
・最大出勤日数:9日
・最小出勤日数:8日
赤×が出勤不可日を表しています。
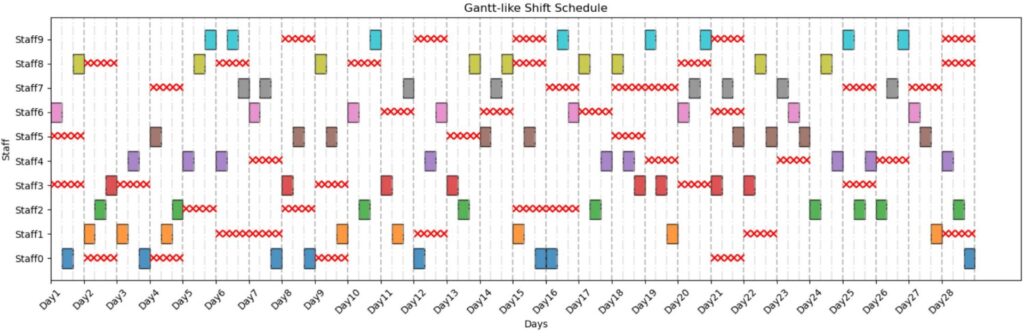
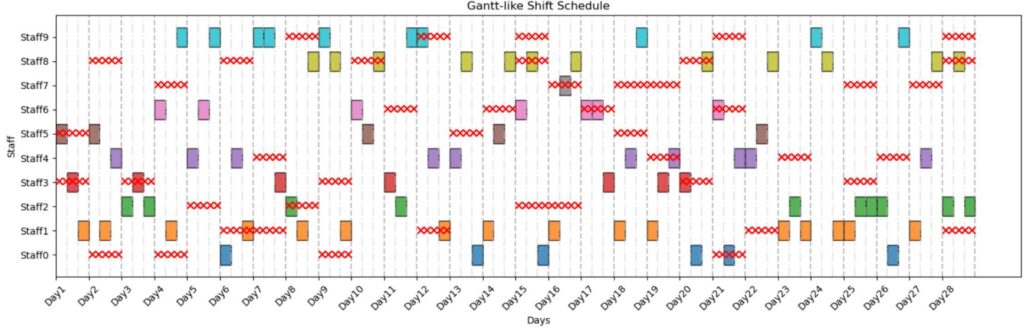
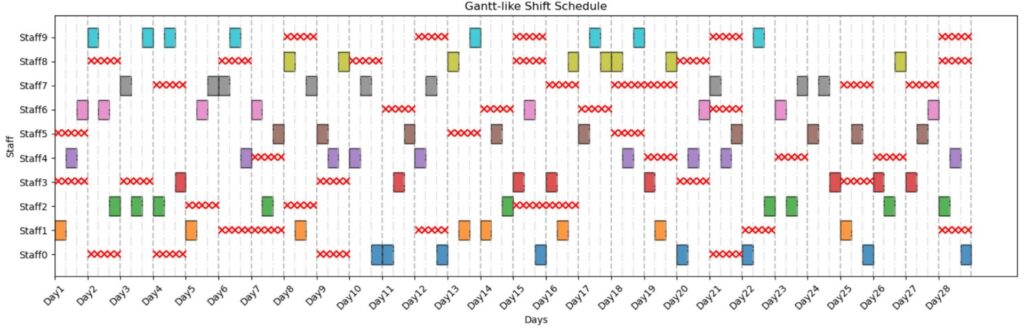
今回の実験では手法1と手法3は制約違反なしの解が得られ、手法2だけ制約違反ありの解が得られました。手法2は制約違反有の解をそもそも生成しないはずなのでおかしいなと思って調べてみると、
「手法2はそもそも実行可能な近傍解を生成できてなかった」
ということが判明しました。というのも近傍解生成を完全ランダムで行っていて、「max_attempt」回生成して実行可能解が得られなかったら諦めるというコードを書いたので、実行可能な近傍解の生成を諦めてしまったようです。
実行可能解しか生成しない手法2だけが実行可能解を出力できなかったのは想定していなかったので、非常に良い勉強になりました。
おわりに
今回は、シフトスケジューリング問題に対して焼きなまし法を適用し、特に制約が多い場合にどう実装を工夫するかを3つの手法で試してみました。
- 手法1:実装しやすいけれど重み付けが大事
- 手法2:評価関数をシンプルに保てる反面、近傍生成が難しくなりがち
- 手法3:実装はやや複雑だが、柔軟かつ効果的に制約を満たす方向へ誘導できる
それぞれを実際に試すことで、最終的に得られる解の質やアルゴリズムの収束特性などを比較することができます。みなさんの環境でもぜひコードを動かしてみて、どんなシフト表が得られるか確かめてみてください。
シフト以外のスケジューリングや割り当て問題にも応用できるので、焼きなまし法の制約管理テクニックとして、ぜひご活用ください!