- シャープレイ値ってなに?
- シャープレイ値ってなにを表しているの?
- シャープレイ値の計算方法は?
- シャープレイ値はどんなところで使われている?
こんにちは!しゅんです!
この記事ではシャープレイ値について解説したいと思います!
シャープレイ値はゲーム理論で登場する用語で、また機械学習の分野でもシャープレイ値が応用されているのを聞いたことがある方もいると思います。ただ計算式を見ても何を計算しているのかよく分からないんですよね。
シャープレイ値\(\phi_i\)の計算式:
\(\phi_i = \sum\limits_{S\subseteq N\setminus\{i\}}\frac{|S|!(n-|S|-1)!}{n!}(v(S\cup\{i\})-v(S))\)
ということでこの記事ではシャープレイ値が何を表しているのか、計算式、そしてシャープレイ値の応用などを解説していきたいと思います!
それではやっていきましょう!
【Udemy講座公開のお知らせ】
このたびUdemyで数理最適化の講座を公開しました!この講座は「数理最適化を勉強してみたいけど数式が多くて難しい…」という方向けに、どうやって最適化問題を定式化すれば良いかを優しく丁寧に解説しています!
シャープレイ値は利益の配分方法の1つ!
まず最初にシャープレイ値って何なの?って話を簡単にしたいと思います。シャープレイ値は協力ゲーム理論で登場する言葉です。
ゲーム理論は大きく分けて協力ゲーム理論と非協力ゲーム理論の2つがあります。違いは名前の通りプレイヤーが協力するかしないかです。協力ゲームではプレイヤーが協力して得られた利益をどう配分するかをよく考えます。
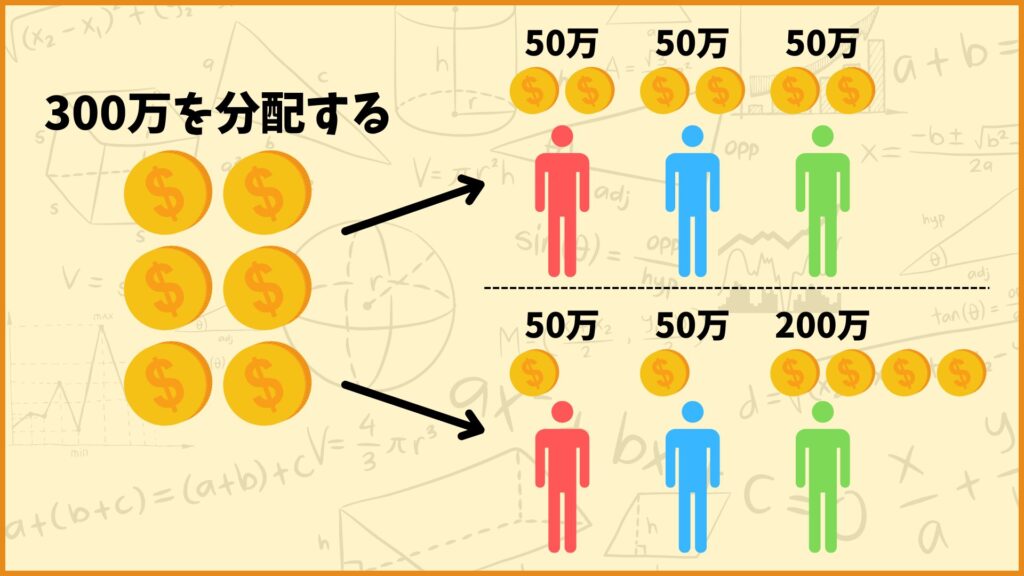
例えば3人のプレイヤーがいて、全員で協力すると300万円の利益が得られるとします。そしたらこの300万円を3人で山分けしないといけないですね。例えば100万、100万、100万に分けたり、200万、50万、50万に分けたり、色々な方法があります。(極端な話300万、0、0も配分方法の1つです。)
このように無数にある配分方法の中でどのような配分を採用すれば良いのかという問題のは非常に重要です。(例えばプレイヤー1とプレイヤー2がたくさん頑張って、プレイヤー3はほとんど何もしていないのに3人に100万ずつ分ける方法はプレイヤー1,2にとっては不公平ですよね。)
その答えの一つとなるのがシャープレイ値(Shapley value)です。シャープレイ値は各プレイヤーがどれだけ貢献したかを基に計算される値で、協力ゲームにおける代表的な配分方法の1つです。
協力ゲームでよく議論される配分方法はシャープレイ値以外にもあります。いくつか例を挙げるとコア(Core)や仁(Nucleolus)は代表的な配分方法です。(もっとちゃんと言うと、コアはいくつかの配分を含む集合です。)気になる人はぜひ調べてみてください!
また300万を(100万, 100万, 100万)に分けたり、(200万,50万,50万)に分けるなど、合計したらちゃんと300万になるような分配方法を表すベクトルはゲーム理論の用語で準配分(preimputation)と呼ばれます。
それでは次にシャープレイ値をどうやって計算するのかを紹介します。
シャープレイ値の計算方法は?
まず最初に具体例を使って説明して、次に文字を使ってより一般的な計算方法の定義を紹介します。
具体例を使って説明する
例えば3人のプレイヤーがいるシチュエーションを考えましょう。それぞれのプレイヤーをプレイヤー1、プレイヤー2、プレイヤー3と呼ぶことにします。

全員が協力した場合、5の利益が得られるとします。3人の内2人が協力した場合、3の利益が得られるとします。プレイヤー1だけだと1、プレイヤー2だけだと1、プレイヤー3だけだと2の利益が得られるとします。また誰も協力しないと利益は0とします。これをまとめると下の表ように書くことができます。なお、これ以降協力するプレイヤーの集合を提携(coalition)と呼びます。
| 協力するプレイヤー(提携) | 利益(特性関数値) |
|---|---|
| 1,2,3 | 5 |
| 1,2 | 3 |
| 1,3 | 3 |
| 2,3 | 3 |
| 1 | 1 |
| 2 | 1 |
| 3 | 2 |
| だれもいない(空集合) | 0 |
なお上の表で示されているように、どんなプレイヤーが協力したら、どれくらいの利益を得ることができるかの対応を表す関数を協力ゲーム理論では特性関数(characteristic function)と呼びます。
シャープレイ値の基本的な考え方は
順番に従って1人ずつプレイヤーが協力する(提携に加わる)
ということです。例えばプレイヤー2→プレイヤー3→プレイヤー1という順番で協力する場合、
誰もいない(利益0)
↓ プレイヤー2が提携に加わる
プレイヤー2だけ(利益1)
↓プレイヤー3が提携に加わる
プレイヤー2,3で協力(利益3)
↓プレイヤー1が提携に加わる
プレイヤー1,2,3で協力(利益5)
上のように利益は変わっていきます。さらにシャープレイ値を計算するときには
(提携にプレイヤーが加わったときに増えた利益)=(そのプレイヤーの貢献度合い)
と考えます。上の例の場合だと、例えば誰もいない状態(空集合)にプレイヤー2が加わったことで利益が1増加していますが、これはプレイヤー2の貢献度が1だと考えることができます。他にも例えばプレイヤー2,3が協力している状態にプレイヤー1が加わったことで利益が2増加していまが、これはプレイヤー1の貢献度が2だと考えることができます。
このように考えると上の例の場合における各プレイヤーの貢献度は
プレイヤー2の貢献度 \((\text{空集合}\emptyset \to \{2\})\) : \(1-0=1\)
プレイヤー3の貢献度 \((\{2\} \to \{2,3\})\) : \(3-1=2\)
プレイヤー1の貢献度 \((\{2,3\}\to\{1,2,3\})\) : \(5-3=2\)
と計算することができます。
ここまでずっと「そのプレイヤーが提携に加わることでどれだけ利益が増えたか」を「貢献度」と呼んでいましたが、正しくはゲーム理論の用語で限界貢献度(marginal contribution)と呼ばれます。
今の話はプレイヤー2→プレイヤー3→プレイヤー1という順番のみを考えていましたが、シャープレイ値を計算するときは全ての順番に対して各プレイヤーの限界貢献度を計算します。3人のプレイヤーがいるので全部で\(3!=6\)通りの順番を考える必要があります。
ということで上の例と同じように全ての順列に対して各プレイヤーの限界貢献度を計算すると下記の表のようにまとめることができます。
| 順列 | プレイヤー1 | プレイヤー2 | プレイヤー3 |
|---|---|---|---|
| (1,2,3) | 1 | 2 | 2 |
| (1,3,2) | 1 | 2 | 2 |
| (2,1,3) | 2 | 1 | 2 |
| (2,3,1) | 2 | 1 | 2 |
| (3,1,2) | 1 | 2 | 2 |
| (3,2,1) | 2 | 1 | 2 |
| 合計 | 9 | 9 | 12 |
| 平均 (シャープレイ値) | 9/6 = 3/2 | 9/6 = 3/2 | 12/6 = 2 |
なお「合計」の行は限界貢献度の総和を表しており、「平均」の行は限界貢献度の平均値を表しています。そして実はこの平均値がシャープレイ値になっているんです。つまり
(シャープレイ値)=(そのプレイヤーが参加したことによって増えた利益(限界貢献度)の平均値)
を表しているんです。各プレイヤーのシャープレイ値を見てみると、プレイヤー1,2は3/2、プレイヤー3は2となっており、3人のシャープレイ値の和は
\((\text{シャープレイ値の総和})=\frac{3}{2}+\frac{3}{2}+2=5\)
となっており、全員で協力したときの利益と一致しています。これは偶然ではなく、シャープレイ値の総和はは必ず全員で協力したときの利益と一致します。

各プレイヤーのシャープレイ値を比較してみると、プレイヤー1,2は3/2で同じ、プレイヤー3だけ2と少し大きい値となっています。これは1人だけの時の利益がプレイヤー1,2は1だけどプレイヤー3だけ2でちょっと多いことが影響しています。
さらにプレイヤー1と2はまったく同じように利益を生み出すプレイヤーなのでシャープレイ値も同じ値になっています。このようにシャープレイ値はどのプレイヤーがどれだけ貢献したかを反映することができる配分となっています。
今回は3人のプレイヤーだったので\(3!=6\)通りの順列を考えましたが、4人のプレイヤーであれば\(4!=24\)通り、10人のプレイヤーであれば\(10!=3628800\)通りの順列を考える必要があります。
文字を使って説明する
それでは次に文字を使ってちゃんとシャープレイ値の定義を理解していきます。まず最初にもう1回シャープレイ値の定義を見てみます。恐らく一度ゲーム理論を勉強したことがある人は下のような定義を見たことがあると思います。
シャープレイ値\(\phi_i\)の定義1:
\(\phi_i = \sum\limits_{S\subseteq N\setminus\{i\}}\frac{|S|!(n-|S|-1)!}{n!}(v(S\cup\{i\})-v(S))\)
シャープレイ値\(\phi_i\)の定義2:
\(\phi_i = \frac{1}{n!}\sum\limits_{\pi\in \Pi_N}\delta(\pi,i)\)
(但し \(\delta(\pi,i)\) は順列 \(\pi\) におけるプレイヤー \(i\) の限界貢献度を表す。)
どちらもシャープレイ値の定義ですが、1つ目の定義の方がよく見るんじゃないでしょうか。ぼくも初めて勉強したときは定義1の方でシャープレイ値を知りました。でも個人的には定義2の方が理解しやすいと思うので、まず定義2の説明をしてから、定義1の方を説明したいと思います。
定義2の方の説明
シャープレイ値\(\phi_i\)の定義2:
\(\phi_i = \frac{1}{n!}\sum\limits_{\pi\in \Pi_N}\delta(\pi,i)\)
(但し \(\delta(\pi,i)\) は順列 \(\pi\) におけるプレイヤー \(i\) の限界貢献度を表す。)
それではまず定義2の方が何を表しているのかを説明します。と言いつつ定義2は「具体例を使って説明する」の考え方を文字で表しただけなんです。
まず最初に上の式に登場する文字が何を表しているのか定義しましょう。
文字の定義:
\(N\) : プレイヤーの集合
\(v\) : 特性関数(提携を入力すると利益を返す)
\(\pi\) : 順列
\(\Pi_N\) : 全ての順列の集合
\(\delta(\pi,i)\):順列 \(\pi\) におけるプレイヤー \(i\) の限界貢献度
\(\phi_i\) : プレイヤー \(i\) のシャープレイ値
いきなり文字が出てもよく分からないので先ほどの「具体例を使って説明する」と照らし合わせて説明します。
まず \(N\) はプレイヤーの集合です。例えば3人のプレイヤーであれば\(N=\{1,2,3\}\)です。
次に \(v\) は特性関数を表します。これは各提携に対してどれだけの利益が得られるのかを表す関数です。例えばプレイヤー2とプレイヤー3が協力したときの利益は3なので\(v(\{2,3\})=3\)となります。全て書くと下記のようになります。
\(v(\{1,2,3\})=5\)
\(v(\{1,2\})=3\)
\(v(\{1,3\})=3\)
\(v(\{2,3\})=3\)
\(v(\{1\})=1\)
\(v(\{2\})=1\)
\(v(\{3\})=2\)
\(v(\emptyset)=0\)
上のように提携と利益の対応関係を表す関数のことをゲーム理論の用語で特性関数(characteristic function)と呼びます。
次に \(\pi\) は順列(提携に加わる順番)を表します。例えばプレイヤー2、プレイヤー3、プレイヤー1の順で提携に加わるときは\(\pi=(2,3,1)\)となります。
次に \(\Pi_N\) は全ての順列の集合です。例えば3人のプレイヤーがいる場合 \(\Pi_N\) は
\(\Pi_N=\{(1,2,3), (1,3,2), (2,1,3), (2,3,1), (3,1,2), (3,2,1)\}\)
となります。
\(\{1,2,3\}\) と \((1,2,3)\) は違う記号です。前者は順番が関係なく、後者は順番が関係あります。
次に \(\delta(\pi,i)\) は順列 \(\pi\) におけるプレイヤー \(i\) の限界貢献度を表しています。例えば「具体例を使って説明する」の所で \(\pi=(2,3,1)\) のときプレイヤー1の限界貢献度は2だったので
\(\delta(\pi,i)=v(\{1,2,3\}) -v(\{2,3\})=5-3=2\)
となります。
最後に \(\phi_i\) はプレイヤー \(i\) のシャープレイ値を表します。例えばプレイヤー1のシャープレイ値が1.5のときは\(\phi_1=1.5\)となります。
それでは計算式の方に入っていきましょう。まず \(\sum_{\pi \in \Pi_N}\delta(\pi,i)\) の部分は全ての順列 \(\pi\) に対してプレイヤー \(i\) の限界貢献度を足し算することを表しています。これは「具体例を使って説明する」の表でいう「合計」の行を表しています。
さらにそれを \(n!\) で割っていますが、これは限界貢献度の平均値を計算しており、「具体例を使って説明する」の表でいうと「平均」の行を表しています。
ということで定義2の計算式が表していることの説明が終わりました。「具体例を使って説明する」の計算が理解できた方にはこの定義もすっと理解できたんじゃないでしょうか。
定義1の方の説明
シャープレイ値\(\phi_i\)の定義1:
\(\phi_i = \sum\limits_{S\subseteq N\setminus\{i\}}\frac{|S|!(n-|S|-1)!}{n!}(v(S\cup\{i\})-v(S))\)
それでは次に定義1の計算式について説明します。定義2の方で説明したように、シャープレイ値は全ての順列に対して各プレイヤーの限界貢献度を計算するんでした。ここで重要なのは、
特性関数に入力するのは集合だからプレイヤーの順番は関係ない
ということです。例えば5人のプレイヤーがいて、プレイヤー1の限界貢献度を計算するとき、順列\(\pi_1 = (3,2,1,4,5)\)と順列\(\pi_2 = (2,3,1,5,4)\)の限界貢献度はどちらも
\(\delta(\pi_1,1)=\delta(\pi_2,1)=v(\{1,2,3\})-v(\{2,3\})\)
と計算することができますね。実は
\((2,3,1,4,5)\)
\((2,3,1,5,4)\)
\((3,2,1,4,5)\)
\((3,2,1,5,4)\)
の4個の順列におけるプレイヤー1の限界貢献度は全て\(v(\{1,2,3\})-v(\{2,3\})\)で計算できます。なぜなら
プレイヤー1よりも前にいるのがプレイヤー2とプレイヤー3なのは一緒
だからです。このようにプレイヤー \(i\) の限界貢献度はプレイヤー \(i\) の前にいるプレイヤーの集合が同じであれば全部同じ値になることが分かります。このことを踏まえて計算式を変形します。
上のように考えれば \(4 \times (v(\{1,2,3\})-v(\{2,3\}))\) とまとめて計算することができ、計算量を削減することができます。
プレイヤー \(i\) よりも前にいるプレイヤーの集合を \(S\) とします。このときのプレイヤー \(i\) の限界貢献度は
\(v(S\cup\{i\})-v(S)\)
と計算されます。例えば\(N=\{1,2,3,4,5\}, S = \{2,3\}, i=1\)であれば上の式は\(v(\{1,2,3\})-v(\{2,3\})\)となります。
続いて限界貢献度が \(v(S\cup\{i\})-v(S)\) と表されるような \(S\) の個数を考えます。上の例では4個でしたが、これは
- プレイヤー \(i\) よりも前にいるプレイヤーたちの並べ替え
- プレイヤー \(i\) よりも後にいるプレイヤーたちの並べ替え
を考えれば良いですね。
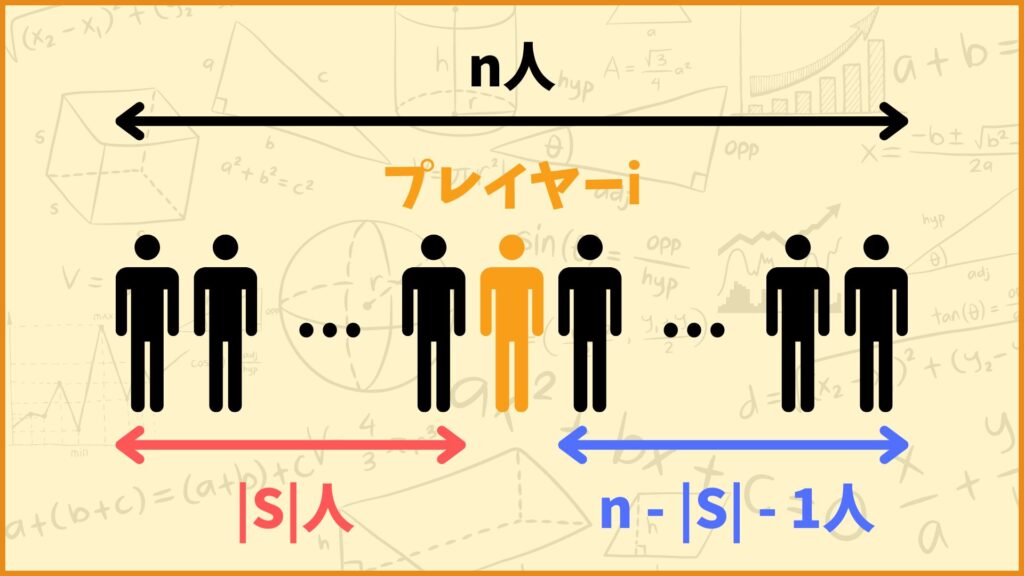
まずプレイヤー \(i\) よりも前にいるプレイヤー数は \(|S|\) 人なので並べ替えの総数は \(|S|!\) 通りあります。一方プレイヤー \(i\) よりも後にいるプレイヤーの数は \(n-|S|-1\) 人なので、並べ替えの総数は \((n-|S|-1)!\) 通りあります。
以上より全ての通りは
\(|S|!(n-|S|-1)!\) 通り
と計算ができます。例えば\(N=\{1,2,3,4,5\}, S = \{2,3\}, i=1\)であれば\(2!\times 2!=4\)通り、\(N=\{1,2,3,4,5\}, S = \{2,3,4\}, i=1\)であれば\(3! \times 1!=6\)と計算できます。すなわち
限界貢献度が\(v(S\cup\{i\})-v(S)\)と計算される場合の数が\(|S|!(n-|S|-1)!\)通りある
ということです。後はこれを全ての場合について足し算して \(n!\) で割ればシャープレイ値を計算することができます。
じゃあ全ての場合ってどんな場合があるのかについて最後に考えてみます。今 \(S\) はプレイヤー \(i\) よりも前にいる人たちの集合を表していますね。すなわちこれは
\(S\subseteq N\setminus\{i\}\)を満たす任意の集合\(S\)
と言い換えることができます。ここで \(A \subseteq B\) は集合 \(A\) が集合 \(B\) の部分集合であることを、\(N\setminus\{i\}\) は集合 \(N\) から要素 \(i\) を除いた集合をそれぞれ表しています。
例:\(N=\{1,2,3,4,5\}, i=1\)
\(S = \{2,3\} \to\) OK
\(S = \{2,4,5\} \to\) OK
\(S = \{2,3,4,5\} \to\) OK
\(S = \emptyset \to\) OK (プレイヤー1が最初に提携に参加するような場合)
\(S= \{1,3,5\} \to\) NG (プレイヤー1がいたらダメ!)
ということでここまでの話をまとめるとプレイヤー \(i\) の限界貢献度の総和は
\((\text{限界貢献度の総和}) = \sum\limits_{S\subseteq N\setminus\{i\}}|S!|(n-|S|-1)!(v(S\cup \{i\})-v(S))\)
と計算されます。これは「具体例を使って説明する」の表の「合計」の行に対応します。そして限界貢献度の平均を計算するためにこれを \(n!\)で割ります。すなわち
\((\text{シャープレイ値}) = \sum\limits_{S\subseteq N\setminus\{i\}}\frac{|S!|(n-|S|-1)!}{n!}(v(S\cup \{i\})-v(S))\)
を計算します。これが「具体例を使って説明する」の表の「平均」の行に対応します。すなわちシャープレイ値を表します。
ということで定義1が言っていることも理解することができました!
定義1の方が一見ややこしくて使いづらそうに見えますが、実は定義1の方が速くシャープレイ値を計算できるんです。というのも、定義2の方では全ての順列を考える必要があるので \(n!\) 回計算する必要がありますが、定義1の方は \(2^{n-1}\) 回の計算で済みます( \(N\setminus \{i\}\) の部分集合は \(2^{n-1}\) 個あるため)。
定義1:\(2^{n-1}\) 回の計算
定義2:\(n!\) 回の計算
これがどれくらい違うのかと言うと
\(n=3\) の場合
定義1:\(2^{3-1}=4\) 回
定義2:\(3!=6\) 回
\(n=5\) の場合
定義1:\(2^{5-1}=16\) 回
定義2:\(5!=120\) 回
\(n=10\) の場合
定義1:\(2^{10-1}=512\) 回
定義2:\(10!=3628800\) 回
と \(n\) が大きくなるにつれて違いが顕著に現れます。従って実際に計算するときは定義1の方で計算する方が速く計算できるはずです(それでも指数的に計算量は大きくなりますが…)。
シャープレイ値って何に応用されているの?
ここまでシャープレイ値の定義の話をたくさんしていきましたが、ここからは応用の話をしたいと思います。実はシャープレイ値は色んな所で応用されています。google scholarとかで「shapley value」と調べると色んなapplicationの論文が引っかかると思います。
本記事ではその中でも特に有名な「投票力指数」と「SHAP」について紹介したいと思います。
投票力指数
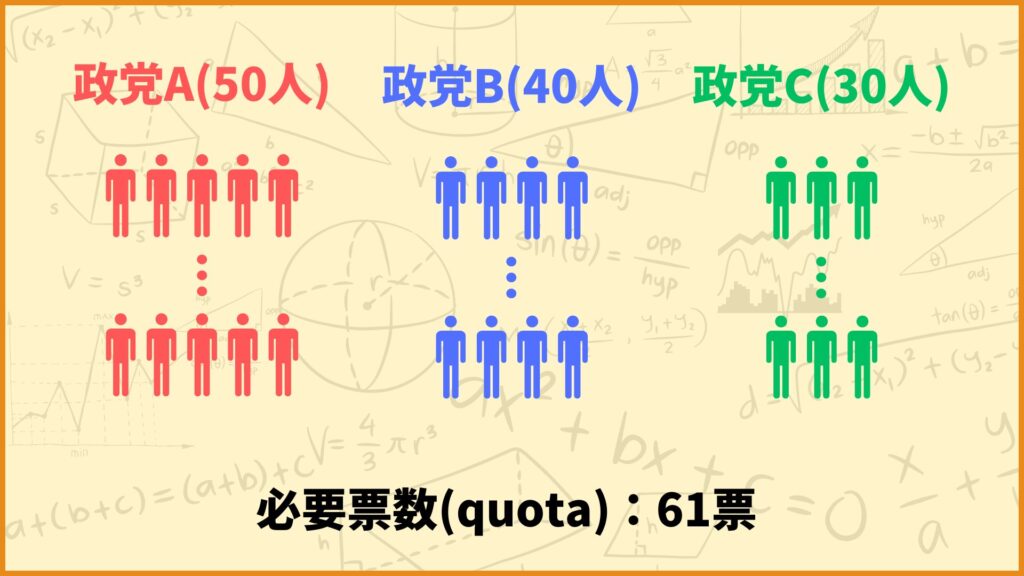
投票力指数(voting power)とは、国会での投票といったシチュエーションにおいてどの政党がどれくらいのパワーを持っているのかを表すために計算される値です。普通に考えるとそれぞれの政党が持つ議席数がそのままパワーを表していそうですが、実はそうでもないんです。
投票力指数を計算するためにはまず上のシチュエーションを協力ゲームとしてモデル化する必要があります。プレイヤーの集合を \(N\)、特性関数を
と定義する協力ゲームを重み付き投票ゲーム(weghted voting game)と呼びます。
重み付き投票ゲームの特性関数をもう少し詳しく説明します。まず各文字を下記のように定義します。
\(w_i\) : 政党 \(i\) が持つ票数
\(q\):議案が可決されるのに必要な票数(quotaと言います)
例えば3つの政党1,2,3があり、それぞれが持つ票数が50票、40票、30票、quotaが61票だとします。このとき各文字が表す値は
\(w_1=50,w_2=40,w_3=30,q=61\)
となります。このとき特性関数は
票数の総和がquota以上であれば1、そうでなければ0
を返します。例えば政党1だけでは50票とquotaに届かないので \(v(\{1\})=0\) となります。一方で政党1,2が協力すれば合計90票でquota以上になるので \(v(\{1,2\})=1\) となります。なお入力が空集合の場合は0を取ります。
それではいくつか具体例を使ってシャープレイ・シュービック指数を計算してみましょう。簡単のために3政党で投票するシチュエーションを考えます。
具体例1
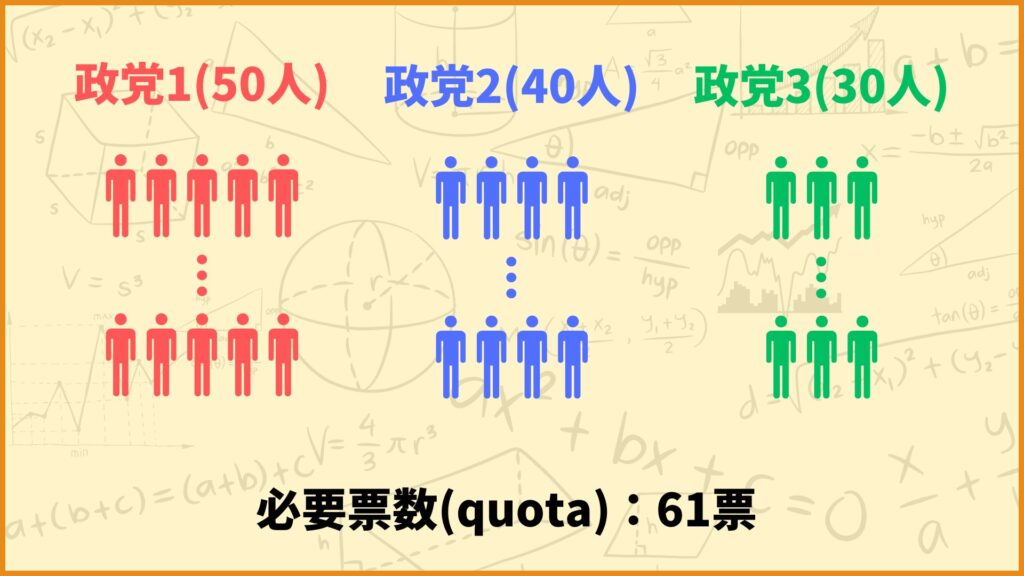
「具体例を使って説明する」の所と同じように表を使ってシャープレイ・シュービック指数を計算してみましょう。
| 順列 | 政党1 | 政党2 | 政党3 |
|---|---|---|---|
| (1,2,3) | 0 | 1 | 0 |
| (1,3,2) | 0 | 0 | 1 |
| (2,1,3) | 1 | 0 | 0 |
| (2,3,1) | 0 | 0 | 1 |
| (3,1,2) | 1 | 0 | 0 |
| (3,2,1) | 0 | 1 | 0 |
| 合計 | 2 | 2 | 2 |
| 平均 (S-S指数) | 2/6 = 1/3 | 2/6 = 1/3 | 2/6 = 1/3 |
ということで上の表を見ると、どの政党もシャープレイ・シュービック指数の値が1/3と計算されています。これは全政党が同じだけのパワーを持っていることを表しています。議席数で言えば政党1と政党3は20票も差があるのに、シャープレイ・シュービック指数だと全く同じパワーを持っていると分析することができます。
具体例2
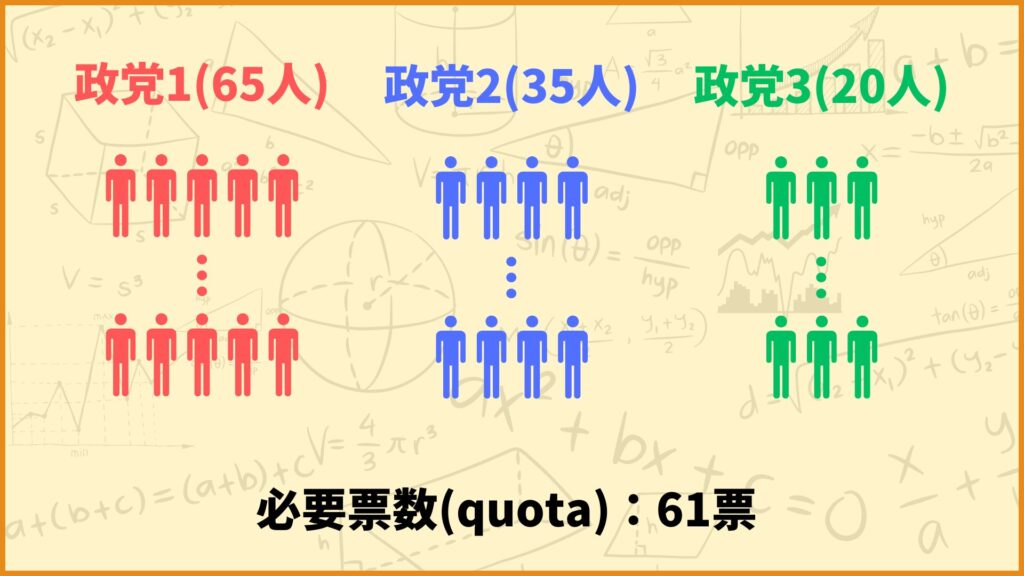
こちらの例についても「具体例を使って説明する」の所と同じように表を使ってシャープレイ・シュービック指数を計算してみましょう。
| 順列 | 政党1 | 政党2 | 政党3 |
|---|---|---|---|
| (1,2,3) | 1 | 0 | 0 |
| (1,3,2) | 1 | 0 | 0 |
| (2,1,3) | 1 | 0 | 0 |
| (2,3,1) | 1 | 0 | 0 |
| (3,1,2) | 1 | 0 | 0 |
| (3,2,1) | 1 | 0 | 0 |
| 合計 | 6 | 0 | 0 |
| 平均 (S-S指数) | 6/6 = 1 | 0/6 = 0 | 0/6 = 0 |
ということで上の表を見ると、政党1のシャープレイ・シュービック指数が1、政党2,3は0と計算されました。なんと政党2,3はそれぞれ35人、20人という議席数を持っているにもかかわらず、投票においては何のパワーも持たないということを表しています。
このシチュエーションを分析してみると、政党1だけでquotaを超えていて、政党2,3が協力してもquotaを下回っていますね。すなわち
政党1がYesと言えば可決、Noと言えば否決
という状況です。従って政党2,3のパワーが0であることは非常に理にかなっていると考えられます。
シャープレイ・シュービック指数は総和が必ず1になります。
ちなみに投票力指数はシャープレイ・シュービック指数以外にもバンザフ指数(Banzhaf index)、ディーガン・パックル指数(Deegan-Packle index)など色々あります。
SHAP

実はシャープレイ値は、ゲーム理論だけでなく機械学習の分野でも広く応用されています。その代表例が SHAP(SHapley Additive exPlanations) です。
近年の機械学習モデルは高い予測性能を持つ一方で「なぜその予測になったのかが分からない」というブラックボックス性が問題になることが多くあります。特に実務ではクライアントに予測結果を説明する際に、単に当たるだけでなく予測の根拠を説明できることが強く求められます。
SHAPは、こうした要求に応えるための手法で、機械学習モデルによる予測に対して、各説明変数がどれだけ予測に貢献したのかを数値として可視化します。その結果、「どの特徴が予測を押し上げ、どの特徴が抑えたのか」を直感的に理解できるようになります。
名前から分かるように、SHAPはシャープレイ値を基に構築されています。ある説明変数を含めた場合と含めなかった場合でどれだけ予測値が変化したかをその説明変数の限界貢献度として扱うことでシャープレイ値を計算します。
すなわち、説明変数の数はプレイヤーの数に対応します。機械学習を勉強したことがある人なら分かると思いますが、説明変数の数が40個、50個になることは珍しくありません。しかし、プレイヤー数が40や50のシャープレイ値を厳密に計算しようとするとめっちゃ時間がかかってしまいます。そこで SHAPでは、シャープレイ値を厳密に計算するのではなく近似的に計算することで、実用的な時間内に各説明変数の貢献度を求められるようにしています。
おわりに
今回はシャープレイ値を紹介しました!
今後もこのようなゲーム理論に関する記事を書いていきます!
最後までこの記事を読んでくれてありがとうございました。
普段は組合せ最適化の記事を書いてたりします。
ぜひ他の記事も読んでみてください!
このブログの簡単な紹介はこちらに書いてあります。
興味があったら見てみてください。
このブログでは経営工学を勉強している現役理系大学生が、経営工学に関することを色々話していきます!
ぼくが経営工学を勉強している中で感じたことや、興味深かったことを皆さんと共有出来たら良いなと思っています。
そもそも経営工学とは何なのでしょうか。Wikipediaによると
経営工学(けいえいこうがく、英: engineering management)は、人・材料・装置・情報・エネルギーを総合したシステムの設計・改善・確立に関する活動である。そのシステムから得られる結果を明示し、予測し、評価するために、工学的な分析・設計の原理・方法とともに、数学、物理および社会科学の専門知識と経験を利用する。
引用元 : 経営工学 – Wikipedia
長々と書いてありますが、要は経営、経済の課題を理系的な観点から解決する学問です。



