こんにちは!しゅんです!
今回は大数の法則について解説していきます!
大数の法則は確率・統計で登場する数学用語です。この記事では大数の法則について図を使って分かりやすく解説していきます。
また今回はpythonを使って大数の法則を確かめていきたいと思います!
それでは解説していきましょう!
統計検定2級に関する他の記事はこちらから見れます!
ぜひ他の記事も読んでみてください!
このブログの簡単な紹介はこちらに書いてあります。
興味があったら見てみてください。
このブログでは経営工学を勉強している現役理系大学生が、経営工学に関することを色々話していきます!
ぼくが経営工学を勉強している中で感じたことや、興味深かったことを皆さんと共有出来たら良いなと思っています。
そもそも経営工学とは何なのでしょうか。Wikipediaによると
経営工学(けいえいこうがく、英: engineering management)は、人・材料・装置・情報・エネルギーを総合したシステムの設計・改善・確立に関する活動である。そのシステムから得られる結果を明示し、予測し、評価するために、工学的な分析・設計の原理・方法とともに、数学、物理および社会科学の専門知識と経験を利用する。
引用元 : 経営工学 – Wikipedia
長々と書いてありますが、要は経営、経済の課題を理系的な観点から解決する学問です。
大数の法則ってなに?
大数の法則を簡単に言うと、コイントスをやったら最初の方はおもての方が出やすいとかうらの方が出やすいとかになるけど、何回もやっていったら両方とも同じくらい出るということを言っています。
例えばコイントスを10回行ってみましょう。もしおもてとうらの出やすさが同じ場合、10回中5回おもて、5回うらが出るはずです。
ところが現実世界ではそうならないですよね。例えば6回もおもてが出たり3回しかおもてが出ないことも全然あります。このように試行回数が少ないときは誤差が非常に大きくなってしまいます。
しかしコイントスの試行回数を100回に増やしてみたらどうでしょう。直観的に考えると10回しか投げないときよりもおもてとうらが同じくらい出そうじゃないですかね。
じゃあ1000回、10000回、100000回という風にどんどん増やしていったらどうなるでしょう。直観的に考えると誤差がどんどん小さくなって、おもてが出る確率もうらが出る確率も0.5に近づいていきそうですよね。

これが大数の法則です。コイントスに関しては、試行回数が少ないうちはおもてが出る確率が0.3や0.6など理論値(0.5)から結構離れているけど、試行回数を増やしていくにつれ誤差は少なくなりおもてが出る確率が0.5に近づいていくということを言っているのが大数の法則です。
大数の法則の具体例
サイコロ
サイコロを投げて1が出る確率を考えてみましょう。理論的には\(\frac{1}{6}\)の確率で1が出るはずですしかし例えばサイコロを12回投げたときに毎回1が2回出るかと言えばそうじゃないですね。

3回出るかもしれないし1回も出ないかもしれません。このように試行回数が少ないときは誤差が大きくなります。
しかしサイコロを投げる回数を120回、1200回、12000回、…と増やしていくとどうなるでしょうか。大数の法則を適用すれば、1が出る確率はだんだん\(\frac{1}{6}\)に近づいていくはずです。
ウェブサイトのクリック数
例えば1カ月のクリック数が平均1000回のウェブサイトがあるとします。このウェブサイトへの1日のクリック数は理論上33.33…回になるはずです。

しかしこのウェブサイトのクリック数を毎日確認してみたときに毎回33クリックくらいになるかと言えば、そうはなりません。
たまたま50回クリックされることもあるし、日によっては10回しかクリックされないかもしれません。このように短い期間で考えてしまうと誤差が大きくなります。
しかしもう少し長いスパンで考えてみると、どんどん誤差は小さくなっていくはずです。大数の法則が成立していますね。
大数の法則をpythonで確かめてみる
最後にpythonを使って大数の法則を確かめてみましょう。今回はコイントスのシミュレーションを行いたいと思います。コイントスは確率0.5のベルヌーイ分布に従うのでベルヌーイ分布をpythonで使いたいと思います。
ベルヌーイ分布はこちらの記事で詳しく解説しています!
プログラムの地域が必要になるので興味がなければプログラムは飛ばして結果だけ見てみてください!
事前準備
pythonで確率・統計を扱うときはscipyというライブラリをよく使います。また数値計算でよく使うnumpy、グラフ作成でよく使うmatplotlibというライブラリもインポートしておきます。
import scipy.stats as stats
import matplotlib.pyplot as plt
import numpy as npベルヌーイ分布を作成する
それでは確率0.5のベルヌーイ分布を作成してみましょう。
# p = 0.5のベルヌーイ分布を作成する
p = 0.5
B = stats.bernoulli(p)ベルヌーイ分布にはBという名前を付けておきました。これ以降はBを使っていきます。
ランダムに10回試行する
それでは実際に試行してみましょう。イメージ的にはコイントスを投げておもてが出れば1、うらが出れば0とする試行を10回行ったときにどういう結果になるのかを見ていきます。
# 10回試行して結果を取得する
samples = B.rvs(size=10)
# 結果を表示する
print(samples)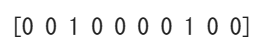
ということで10回試行してみました。おもて(1)が2回しか出ていないですね。この結果を基にするとおもてが出る確率が0.2になってしまいます。
このプログラムはランダムに実行されるので結果は毎回異なります。ということでもう何回か実行してみましょう。
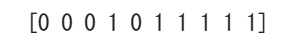


ということで3回実行してみました。2回目はちょうどおもてが5回出ていますが、1回目は6回、3回目に至っては8回もおもてが登場していますね。
このように試行回数が少ないと誤差が非常に出やすいです。
試行回数を増やす
それでは試行回数を10回から100回、10000回、100000回、1000000回と増やしてみましょう。毎回結果を表示するのは大変なので、今回はおもてが出た割合を表示するようなプログラムにします。
# 試行回数のリストを作成
trial = [10,100,1000,10000,100000,1000000]
# 10回、100回、...、1000000回と試行回数を増やす
for num in trial:
# 結果をsampleに格納
samples = B.rvs(size=num)
# 試行回数を割合に変換
prob = samples.sum()/num
# 割合を表示する
print(f"{num}回 :", prob)
ということで各回数でおもてが出る割合がどれくらいかが計算できました。これを見ると試行回数が増えるにつれておもてが出る割合がどんどん0.5に近づいていっているのが分かりますね。これが大数の法則です。
グラフで視覚的に理解する
最後にこのことをグラフを使って理解していきましょう。横軸を試行回数、縦軸をおもてが出る割合として折れ線グラフを作成してみます。
# 結果を格納する空リストを作成
result = []
# 試行回数のリストを作成
trial = [10,100,1000,10000,100000,1000000]
# 10回、100回、...、1000000回と試行回数を増やす
for num in trial:
# 結果をsampleに格納
samples = B.rvs(size=num)
# 試行回数を割合に変換
prob = samples.sum()/num
# 割合をresultに格納
result.append(prob)
# 折れ線グラフを作成
plt.plot(trial, result, label='Simulated',color = "blue",marker = "o",alpha=0.5)
plt.hlines(0.5,10,1000000, label='Theoretical', color = "orange", alpha = 1)
plt.xscale("log")
plt.xlabel("Number of trials")
plt.ylabel("Probability")
plt.title("Coin Tosses And The Law Of Large Numbers")
plt.legend()
plt.show()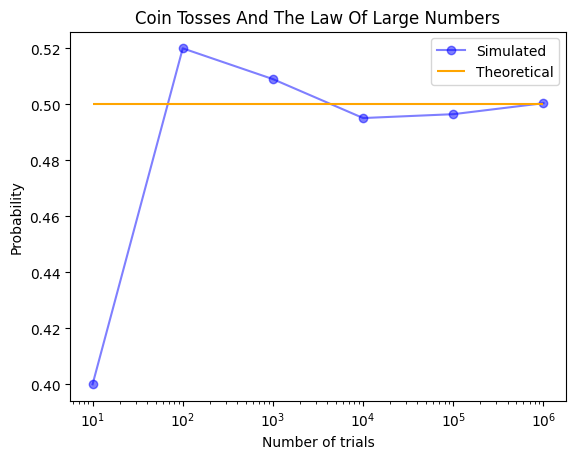
ということでグラフを作成することができました。青線が試行回数を増やしていったときにおもてが出る割合がどのように推移しているかを表しており、橙線が理論値0.5を表しています。
やはり試行回数を増やしていくと青線はどんどん橙線に近づいていっているのが分かりますね。
0.5からどれくらい離れているかを絶対誤差で計算してみましょう。絶対誤差は実測値から理論値を引いたものの絶対値です。
# 誤差を格納するための空リストを作成
AE=[]
# 誤差を計算
for i in range(len(result)):
AE.append(abs(result[i] - 0.5))
# 折れ線グラフを作成
plt.plot(trial, AE,color = "green",marker = "o",alpha=0.5)
plt.xscale("log")
plt.xlabel("Number of trials")
plt.ylabel("Absolute Error")
plt.title("Coin Tosses And The Law Of Large Numbers")
plt.show()
ということで試行回数を増やすと誤差がだんだん0に近づいていることが分かりますね。ちゃんと大数の法則が成り立っています。
おわりに
いかがでしたか。
今回の記事では大数の法則について解説していきました。
今後もこのような経営工学に関する記事を書いていきます!
最後までこの記事を読んでくれてありがとうございました。




