こんにちは!しゅんです!
今回は標本平均について解説していきます!
標本平均は確率・統計で登場する数学用語です。この記事では標本平均について図を使って分かりやすく解説していきます。
また今回はpythonを使って標本平均を扱っていきたいと思います!
それでは解説していきましょう!
統計検定2級に関する他の記事はこちらから見れます!
ぜひ他の記事も読んでみてください!
このブログの簡単な紹介はこちらに書いてあります。
興味があったら見てみてください。
このブログでは経営工学を勉強している現役理系大学生が、経営工学に関することを色々話していきます!
ぼくが経営工学を勉強している中で感じたことや、興味深かったことを皆さんと共有出来たら良いなと思っています。
そもそも経営工学とは何なのでしょうか。Wikipediaによると
経営工学(けいえいこうがく、英: engineering management)は、人・材料・装置・情報・エネルギーを総合したシステムの設計・改善・確立に関する活動である。そのシステムから得られる結果を明示し、予測し、評価するために、工学的な分析・設計の原理・方法とともに、数学、物理および社会科学の専門知識と経験を利用する。
引用元 : 経営工学 – Wikipedia
長々と書いてありますが、要は経営、経済の課題を理系的な観点から解決する学問です。
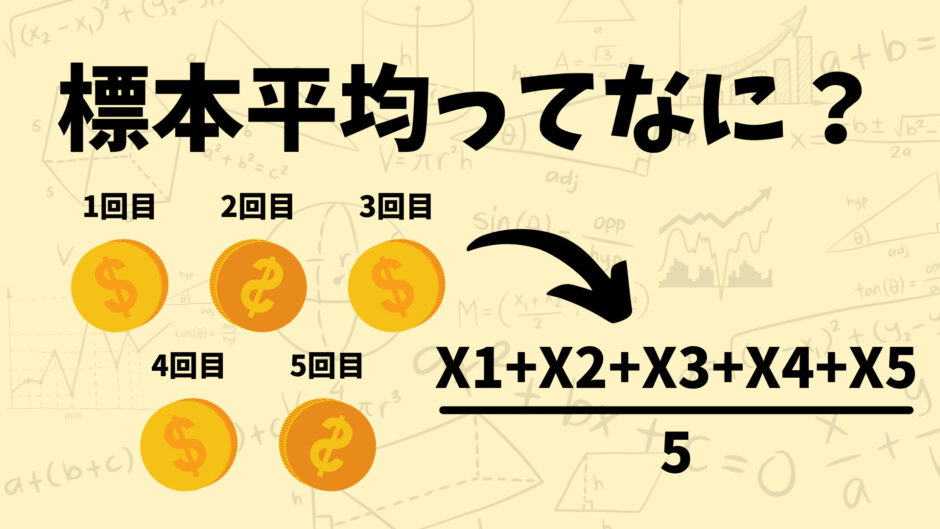
標本平均ってなに?
標本平均をザックリ説明するとデータの平均です。(名前のまんまです笑)
標本平均を考えるためにコイントスの例を使って説明します。おもてが出る確率が0.5のコインを使ってコイントスをします。このコイントスは\(p=0.5\)のベルヌーイ分布に従います。
ベルヌーイ分布はこちらの記事で詳しく解説しています!
このコイントスを5回やった結果おもてが3回出たとします。ちなみにベルヌーイ試行を複数回行ったときその成功回数は二項分布に従いますね。

おもてを1、うらを0として考えていきます。このとき平均どれくらいの割合でおもてが出たかを計算していきます。計算方法は1回目から5回目までの結果を足し算して試行回数で割ります。

ということで計算して出てきた0.6という数字が今回の標本平均となります。やってることはただ単に結果の平均を計算しているだけなのでそこまで難しくはないと思います。
このことを踏まえてより一般的な表現をしてみましょう。今\(i\)回目での結果を\(X_i\)として考えます。(この\(X_i\)のことを確率変数って呼びます。)
この試行を\(n\)回やったときの標本平均を計算したいと思います。つまり\(X_1, \; X_2, …, \; X_n\)を足して\(n\)で割ります。
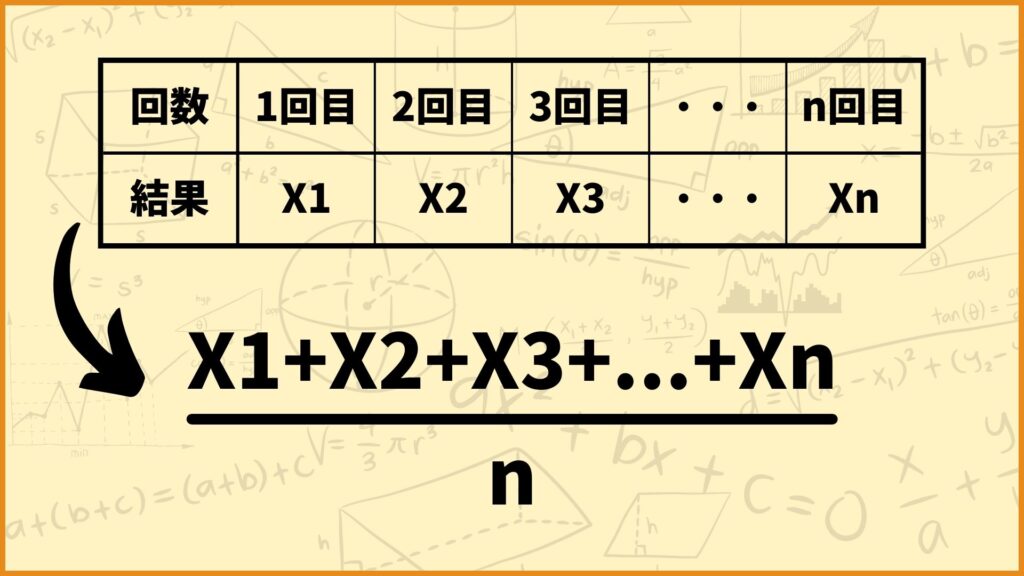
\(\frac{X_1+X_2+X_3+…+X_n}{n}\)
\(=\frac{1}{n}\sum\limits_{i=1}^n X_i\)
というわけで標本平均の計算式を表すことができました。
標本とは実験や調査によって実際に得られるデータのことで、今回で言うとコイントスを実際にやっておもてとうらのどっちが出たかというデータです。これら標本の平均値を計算しているから標本平均と言うんですね。
標本平均の期待値と分散
確率変数の平均を計算することで標本平均が求められるので、標本平均も確率変数となります。(要は標本平均がどの値を取るかも確率的に決まるってことです。)
少し難しいですが最初に標本平均の期待値、分散の計算式を出してから具体例を用いて解説したいと思います。

確率変数\(X_1, \; X_2, …, \; X_n\)が独立に平均\(\mu\)、分散\(\sigma^2\)の確率分布に従うと仮定します。独立とは簡単に言うとある事象が他の事象の結果に影響を及ぼさないことです。
このとき標本平均の期待値と分散は下のようになります。
期待値:\(\mu\)
分散:\(\frac{\sigma^2}{n}\)
標本平均の期待値は元の確率分布の期待値と同じですが、分散は元の確率分布の分散を\(n\)で割った値になります。
イメージ的には標本の数が大きくなるにつれてデータのばらつきがどんどん小さくなっていく感じです。
例えばコイントスを考えてみましょう。コイントスを5回行う試行は、確率変数\(X_1, \; X_2, …, \; X_5\)が独立に平均\(\frac{1}{2}\)、分散\(\frac{1}{4}\)のベルヌーイ分布に従うと仮定できます。
このとき標本平均の期待値と分散は下のようになります。
期待値:\(\frac{1}{2}\)
分散:\(\frac{1}{20}\)
期待値と分散の式の導出
標本平均の期待値と分散の式を導出します。数学の知識が必要なので難しい場合は飛ばしてください。
まず確率変数\(X_1, \; X_2,…,_;X_n\)が独立に平均\(\mu\)、分散\(\sigma\)の確率分布に従うことを式にすると下のようになります。
\(E[X_1]=E[X_2]=…=E[X_n]=\mu\)
\(V[X_1]=V[X_2]=…=V[X_n]=\sigma^2\)
\(E[X]\)は確率変数\(X\)の期待値(平均)を表し、\(V[X]\)は確率変数\(X\)の分散を表します。標本平均を\(\bar{X}\)とすると\(\bar{X}\)は下のように表せます。
\(\bar{X}=\frac{X_1+X_2+…+X_n}{n}\)
ここで期待値の性質として、定数\(a,b\)と確率変数\(X,Y\)に対して以下のことが成り立ちます。
\(E[aX+bY]=aE[X]+bE[Y]\)
また分散の性質として、定数\(a,b\)と独立な確率変数\(X,Y\)に対して以下のことが成り立ちます。
\(V[aX+bY]=a^2V[X]+b^2V[Y]\)
これらの性質を使って\(E[\bar{X}]\)と\(V[\bar{X}]\)を求めます。
\(\;\;\;\;E[\bar{X}]\)
\(=E[\frac{X_1+X_2+…+X_n}{n}]\)
\(=\frac{1}{n}E[X_1]+\frac{1}{n}E[X_2]+…+\frac{1}{n}E[X_n]\)
\(=\frac{\mu}{n}+\frac{\mu}{n}+…+\frac{\mu}{n}\)
\(=\mu\)
\(\;\;\;\;V[\bar{X}]\)
\(=V[\frac{X_1+X_2+…+X_n}{n}]\)
\(=\frac{1}{n^2}V[X_1]+\frac{1}{n^2}V[X_2]+…+\frac{1}{n^2}V[X_n]\)
\(=\frac{\sigma}{n^2}+\frac{\sigma}{n^2}+…+\frac{\sigma}{n^2}\)
\(=\frac{n\sigma}{n^2}\)
\(=\frac{\sigma^2}{n}\)
pythonで標本平均を扱う
最後にpythonを使って標本平均を扱いたいと思います。プログラミングの知識が必要なので、分からなければプログラムの所は飛ばして結果だけ確認してみてください。
事前準備
pythonで確率・統計を扱うときはscipyというライブラリをよく使います。その中でも今回は二項分布を扱いたいのでbinomをインポートします。また数値計算でよく使うnumpy、グラフ作成でよく使うmatplotlibというライブラリもインポートしておきます。
import scipy.stats as stats
from scipy.stats import binom
import matplotlib.pyplot as plt
import numpy as np二項分布を使って標本平均を求める
まずは独立にベルヌーイ分布に従う確率変数の標本平均を求めます。ベルヌーイ試行を複数回行うことは二項分布を使って表すことができるので、pythonでは二項分布を使いたいと思います。
\(n=5, \; p=0.5\)の二項分布を使いたいと思います。つまりおもてが出る確率が0.5のコイントスを5回行う試行の標本平均を求めたいと思います。

ベルヌーイ分布に従う確率変数の標本平均を求めるとき、分子の値は二項分布に従います。すなわちこの二項分布の試行結果を試行回数で割った値が標本平均の分布に従うと言うわけです。
試しにこの標本平均の分布に従う確率変数を10回生成してみましょう。
# 試行回数と成功確率を指定
n = 5
p = 0.5
# 10回ループさせる
for i in range(10):
print(stats.binom.rvs(n=n, p=p)/n) # 確率変数を生成する
こんな感じになりました。このプログラムでは確率変数がランダムに生成されるので実行するごとに違う結果が得られます。これを見ると0.4が出る割合が一番多いですね。理論的には平均0.5になるはずなのでまあまあ近いですね。
標本平均をグラフにする
次にこの標本平均の分布をグラフにしてみましょう。\(n=5, \; p= 0.5\)として、この標本平均をランダムに10000個生成したときの様子を棒グラフで表します。
横軸に標本平均の値、縦軸に出現割合を取って棒グラフを作成していきます。
# 試行回数と成功確率を指定
n = 5
p = 0.5
# 結果を格納する空リストを作成
result = []
# 10000回ループさせる
for i in range(10000):
result.append(stats.binom.rvs(n=n, p=p)/n) # 確率変数を生成してresultに格納
# 出現割合を計算
hist, bins = np.histogram(result, bins=(np.arange(n+2)-0.5)/n)
hist = hist / sum(hist) # 出現割合に変換
# resultのヒストグラムを描画
plt.bar(bins[:-1]+0.5/n, hist, width=1/n, color = "blue", alpha = 0.5, edgecolor="black", linewidth=1)
plt.xlabel("Percentage of Successes")
plt.ylabel("Appearance Ratio")
plt.title("Sample Mean")
plt.show()
ということでグラフにできました。10000回試行しているのでほぼ理論的な標本平均の分布と一致しているはずです。0.4と0.6の割合が最も大きく、そこから離れるにしたがってどんどん小さくなっています。
確率変数の数nを増やす
それでは標本平均に用いる確率変数の数を増やしていきましょう。これまでは\(n=5\)でやっていましたが、ここでは\(n=50\)に増やしてみたいと思います。イメージ的にはコイントスを行う回数を5回から50回に増やす感じです。
そのため成功回数も0回から50回まで幅広い値を取るので標本平均の値はより細かい数字になります。試しに標本平均をランダムに10個生成してみましょう。
# 試行回数と成功確率を指定
n = 50
p = 0.5
# 10回ループさせる
for i in range(10):
print(stats.binom.rvs(n=n, p=p)/n) # 確率変数を生成する
たまに0.38みたいに少し離れている値もありますが、だいたい0.5あたりに集中していますね。\(n\)が大きくなると0.5に近づいているように見えますね。この性質は大数の法則と呼ばれます。
大数の法則はこちらの記事で詳しく解説しています!
次にこの標本平均の分布をグラフにしてみましょう。\(n=50, \; p= 0.5\)として、この標本平均をランダムに10000個生成したときの様子を棒グラフで表します。
横軸に標本平均の値、縦軸に出現割合を取って棒グラフを作成していきます。
# 試行回数と成功確率を指定
n = 50
p = 0.5
# 結果を格納する空リストを作成
result = []
# 10000回ループさせる
for i in range(10000):
result.append(stats.binom.rvs(n=n, p=p)/n) # 確率変数を生成してresultに格納
# 出現割合を計算
hist, bins = np.histogram(result, bins=(np.arange(n+2)-0.5)/n)
hist = hist / sum(hist) # 出現割合に変換
# resultのヒストグラムを描画
plt.bar(bins[:-1]+0.5/n, hist, width=1/n, color = "blue", alpha = 0.5, edgecolor="black", linewidth=1)
plt.xlabel("Percentage of Successes")
plt.ylabel("Appearance Ratio")
plt.title("Sample Mean")
plt.show()
試行回数が増えたので標本平均が取りうる値のバリエーションが先ほどよりも多くなりました。
おわりに
いかがでしたか。
今回の記事では標本平均について解説していきました。
今後もこのような経営工学に関する記事を書いていきます!
最後までこの記事を読んでくれてありがとうございました。