- ベルマンフォード法ってなに?
- ベルマンフォード法の手順は?
- ベルマンフォード法って負閉路を検知できるの?
こんにちは!しゅんです!
今回の記事はベルマンフォード法について解説していきます!
ベルマンフォード法(Bellman–Ford Algorithm)はグラフ理論で登場する用語で、重み付き有向グラフにおいて最短経路を求める方法の1つです。
このアルゴリズムの良い所は辺の重みが負の場合でも適用できるということです。
この記事ではベルマンフォード法ってどうやってやるのかを1つずつ丁寧に解説していこうと思います!
それではやっていきましょう!
普段は組合せ最適化の記事を書いてたりします。
ぜひ他の記事も読んでみてください!
このブログの簡単な紹介はこちらに書いてあります。
興味があったら見てみてください。
このブログでは経営工学を勉強している現役理系大学生が、経営工学に関することを色々話していきます!
ぼくが経営工学を勉強している中で感じたことや、興味深かったことを皆さんと共有出来たら良いなと思っています。
そもそも経営工学とは何なのでしょうか。Wikipediaによると
経営工学(けいえいこうがく、英: engineering management)は、人・材料・装置・情報・エネルギーを総合したシステムの設計・改善・確立に関する活動である。そのシステムから得られる結果を明示し、予測し、評価するために、工学的な分析・設計の原理・方法とともに、数学、物理および社会科学の専門知識と経験を利用する。
引用元 : 経営工学 – Wikipedia
長々と書いてありますが、要は経営、経済の課題を理系的な観点から解決する学問です。
ベルマンフォード法のアルゴリズム
STEP.1 最短距離の初期値を始点は0、それ以外の頂点は∞に設定する。
STEP.2 始点から各頂点に対して高々1本の辺を使って到達できる最短経路を探す。
最短距離を更新する。
STEP.3 始点から各頂点に対して高々2本の辺を使って到達できる最短経路を探す。
最短距離を更新する。
STEP.4 始点から各頂点に対して高々3本の辺を使って到達できる最短経路を探す。
最短距離を更新する。
.
. 高々\(n-1\)本になるまで繰り返す。(\(n\)は頂点数)
.
文字だけで説明してもあまりよく分からないので下のグラフを使ってベルマンフォード法のアルゴリズムを説明したいと思います。
それでは1つずつ解説していきます!
始点からある頂点への最短経路を探すときのポイントは、
「その辺がどの頂点に向かうかで辺をグループ分けする」
ということです。このことを踏まえて説明を読むと理解しやすいと思います。
STEP.1 初期値の設定
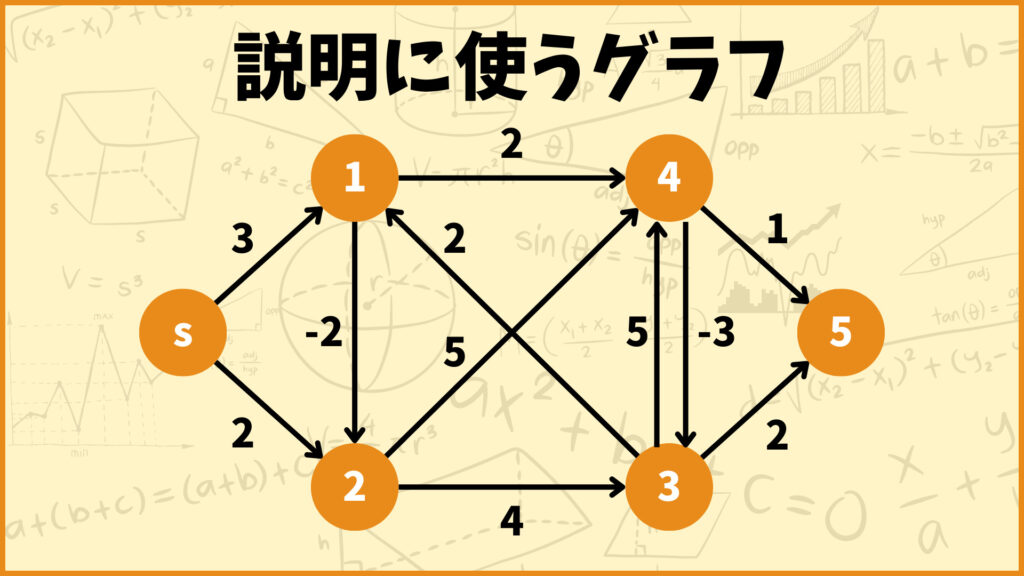
まずは最短距離の初期値を設定します。始点を頂点\(s\)とすると、頂点\(s\)は\(0\)、それ以外の頂点は\(\infty\)と設定します。

これ以降は上図のグラフと表を使って説明したいと思います。この表は各行が各頂点、各列が使って良い辺数の最大値を表しています。
例えば2の列、3の行のマスには「辺を高々2本使うときの始点\(s\)から頂点3の最短距離」を記入します。
そしてこの初期値は「高々0本の辺を使うときの始点\(s\)から各頂点への最短距離」だと思ってください。高々0本ってこと辺を一本も使っちゃいけないので当然始点の初期値は\(0\)、それ以外の頂点の初期値は\(\infty\)となります。
STEP.2 高々1本の辺を使う
それでは高々1本の辺を使うときの、始点\(s\)から各頂点までの最短距離を求めて表に記入していきましょう。
最短距離を求めるときはグラフ中の辺を、「どの頂点に向かうか」でグループ分けすると理解しやすいと思います。

ということでどの頂点に向かうかで辺を色分けした結果が上図のようになります。まずは頂点1について最短距離を考えてみましょう。頂点1に向かう辺は辺\((s,1),(3,1)\)の2つです。
辺\((u,v)\)を使うときの、始点\(s\)から頂点\(v\)への最短距離は以下の式で計算できます。
「頂点\(u\)の上の白黒の数字」+「辺\((u,v)\)の重み」
そのため例えば辺\((s,1)\)を使った場合の最短距離は始点\(s\)の初期値に辺\((s,1)\)の重みを足すことで計算できます。また辺\((3,1)\)を使った場合の最短距離は頂点3の初期値に辺\((3,1)\)の重みを足すことで計算できます。
辺\((s,1)\)を使うときの最短距離:0+3 = 3
辺\((3,1)\)を使うときの最短距離:∞+2 = ∞
この2つを比べると辺\((s,1)\)を使った方が距離が短いことが分かるので、高々1本の辺を使ったときの始点\(s\)から頂点1までの最短距離は3であることが分かりました。
なぜ各頂点の上に書いてある白黒の数字に辺の重みを足すことで計算できるの?

高々\(n\)本の辺を使った最短距離を考えます。このとき各頂点の上に書いてある白黒の数字は「高々\(n-1\)本の辺を使うときの最短距離」を表しています。
その白黒の数字に辺の重みを足すという計算で出た値は
「高々\(n\)本の辺を使って到達できる経路の距離」
であることが保証されます。
同じように頂点2についても考えると辺\((s,2)\)と辺\((1,2)\)のうち辺\((s,2)\)を使った方が距離が短いことが分かりますね。
辺\((s,2)\)を使うときの最短距離:0+2 = 2
辺\((1,2)\)を使うときの最短距離:∞-2 = ∞
頂点3,4,5に関してはどの辺を通っても最短距離が∞となります。ということで全ての頂点に対して高々1本の辺を使うときの最短距離が計算できたので、あの表を更新しましょう。
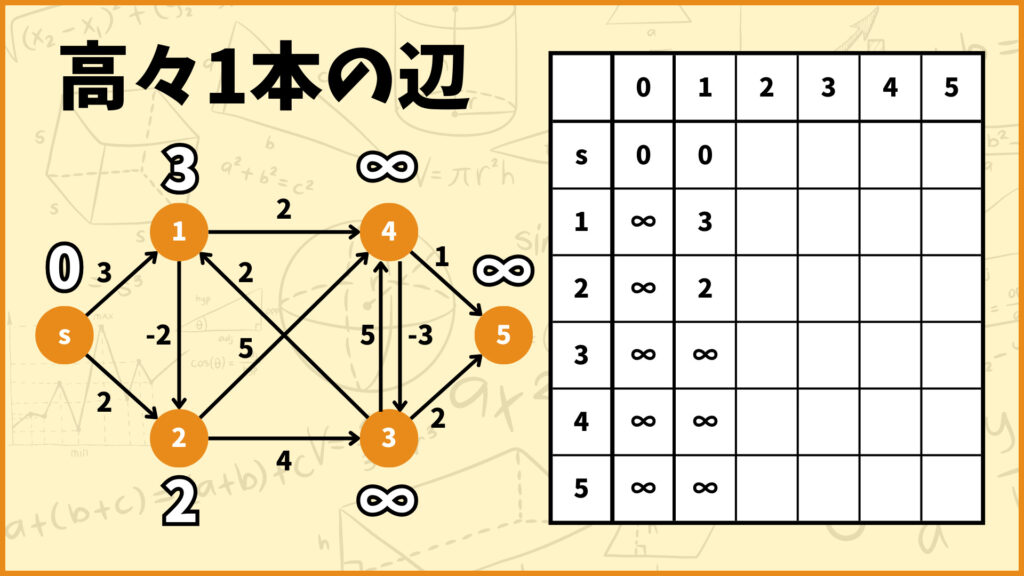
表の更新に伴って各頂点の上に書いてある白黒の数字も更新します。この時点でこれら白黒の数字は
「高々1本の辺を使うときの、始点\(s\)から各頂点への最短距離」
を表していることに注意してください。
STEP.3 高々2本の辺を使う
次に高々2本の辺を使うときの各頂点への最短距離を考えていきましょう。やり方はSTEP.2の時と同じです。
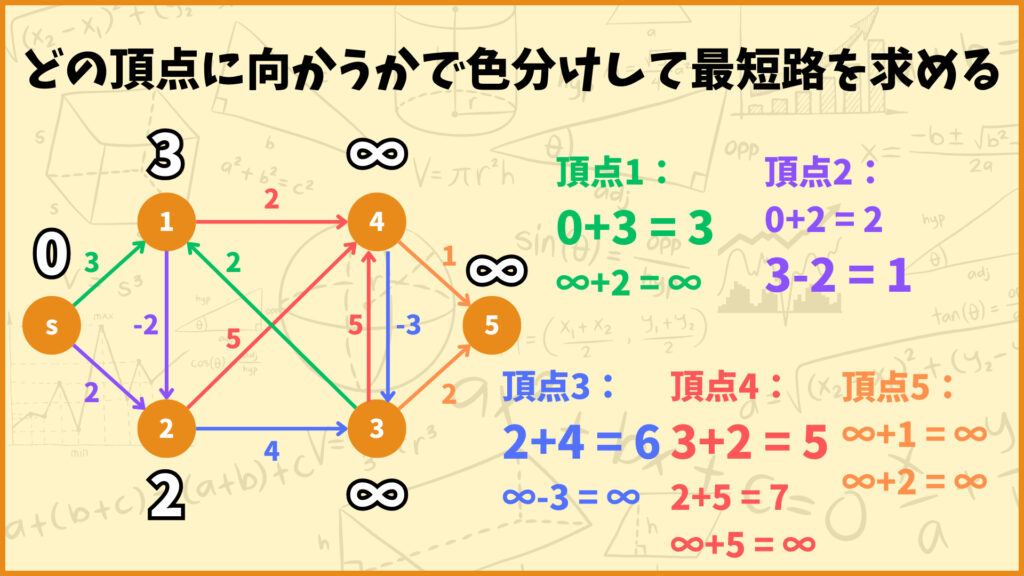
頂点1
頂点1に向かう辺は辺\((s,1),(3,1)\)の2つあります。それぞれの辺を使った場合の最短距離を計算すると以下のようになります。
辺\((s,1)\)を使うときの最短距離:0+3 = 3
辺\((3,1)\)を使うときの最短距離:∞+2 = ∞
ということで辺\((s,1)\)を使う経路の方が距離が短いことが分かりました。
頂点2
頂点3に向かう辺は辺\((s,2),(1,2)\)の2つあります。それぞれの辺を使った場合の最短距離を計算すると以下のようになります。
辺\((s,2)\)を使うときの最短距離:0+2 = 2
辺\((1,2)\)を使うときの最短距離:3-2 = 1
ということで辺\((1,2)\)を使う経路の方が距離が短いことが分かりました。
高々1本の辺を使うときは辺\((s,2)\)を使うのが最短でしたが、初期値が更新されたので高々2本の辺を使うときは辺\((1,2)\)を使う方が距離が短くなっています。
頂点3
頂点3に向かう辺は辺\((2,3),(4,3)\)の2つあります。それぞれの辺を使った場合の最短距離を計算すると以下のようになります。
辺\((2,3)\)を使うときの最短距離:2+4 = 6
辺\((4,3)\)を使うときの最短距離:∞-3 = ∞
ということで辺\((2,3)\)を使う経路の方が距離が短いことが分かりました。
頂点4
頂点4に向かう辺は辺\((1,4),(2,4),(3,4)\)の2つあります。それぞれの辺を使った場合の最短距離を計算すると以下のようになります。
辺\((1,4)\)を使うときの最短距離:3+2 = 5
辺\((2,4)\)を使うときの最短距離:2+5 = 7
辺\((3,4)\)を使うときの最短距離:∞+5 = ∞
ということで辺\((1,4)\)を使う経路が最短距離だと分かりました。
頂点5
頂点4に向かう辺は辺\((1,4),(2,4),(3,4)\)の2つあります。それぞれの辺を使った場合の最短距離を計算すると以下のようになります。
辺\((4,5)\)を使うときの最短距離:∞+1 = ∞
辺\((3,5)\)を使うときの最短距離:∞+2 = ∞
ということでどちらの辺を使っても最短距離は∞のままでした。
全ての頂点に対して高々2本の辺を使うときの最短距離が求まったのであの表を更新しましょう。

表の更新に伴って各頂点の上に書いてある白黒の数字も更新します。この時点でこれら白黒の数字は
「高々2本の辺を使うときの、始点\(s\)から各頂点への最短距離」
を表していることに注意してください。
STEP.4 高々3本の辺を使う
次に高々3本の辺を使うときの各頂点への最短距離を考えていきましょう。

頂点1
頂点1に向かう辺は辺\((s,1),(3,1)\)の2つあります。それぞれの辺を使った場合の最短距離を計算すると以下のようになります。
辺\((s,1)\)を使うときの最短距離:0+3 = 3
辺\((3,1)\)を使うときの最短距離:6+2 = 8
ということで辺\((s,1)\)を使う経路の方が距離が短いことが分かりました。
頂点2
頂点3に向かう辺は辺\((s,2),(1,2)\)の2つあります。それぞれの辺を使った場合の最短距離を計算すると以下のようになります。
辺\((s,2)\)を使うときの最短距離:0+2 = 2
辺\((1,2)\)を使うときの最短距離:3-2 = 1
ということで辺\((1,2)\)を使う経路の方が距離が短いことが分かりました。
頂点3
頂点3に向かう辺は辺\((2,3),(4,3)\)の2つあります。それぞれの辺を使った場合の最短距離を計算すると以下のようになります。
辺\((2,3)\)を使うときの最短距離:1+4 = 5
辺\((4,3)\)を使うときの最短距離:5-3 = 2
ということで辺\((4,3)\)を使う経路の方が距離が短いことが分かりました。
高々2本の辺を使うときは辺\((2,3)\)を使うのが最短でしたが、最短距離が更新されたので高々3本の辺を使うときは辺\((4,3)\)を使う方が距離が短くなっています。
頂点4
頂点4に向かう辺は辺\((1,4),(2,4),(3,4)\)の2つあります。それぞれの辺を使った場合の最短距離を計算すると以下のようになります。
辺\((1,4)\)を使うときの最短距離:3+2 = 5
辺\((2,4)\)を使うときの最短距離:1+5 = 6
辺\((3,4)\)を使うときの最短距離:6+5 = 11
ということで辺\((1,4)\)を使う経路が最短距離だと分かりました。
頂点5
頂点4に向かう辺は辺\((1,4),(2,4),(3,4)\)の2つあります。それぞれの辺を使った場合の最短距離を計算すると以下のようになります。
辺\((4,5)\)を使うときの最短距離:5+1 = 6
辺\((3,5)\)を使うときの最短距離:6+2 = 8
ということで辺\((4,5)\)を使う経路が最短距離だと分かりました。
全ての頂点に対して高々3本の辺を使うときの最短距離が求まったのであの表を更新しましょう。
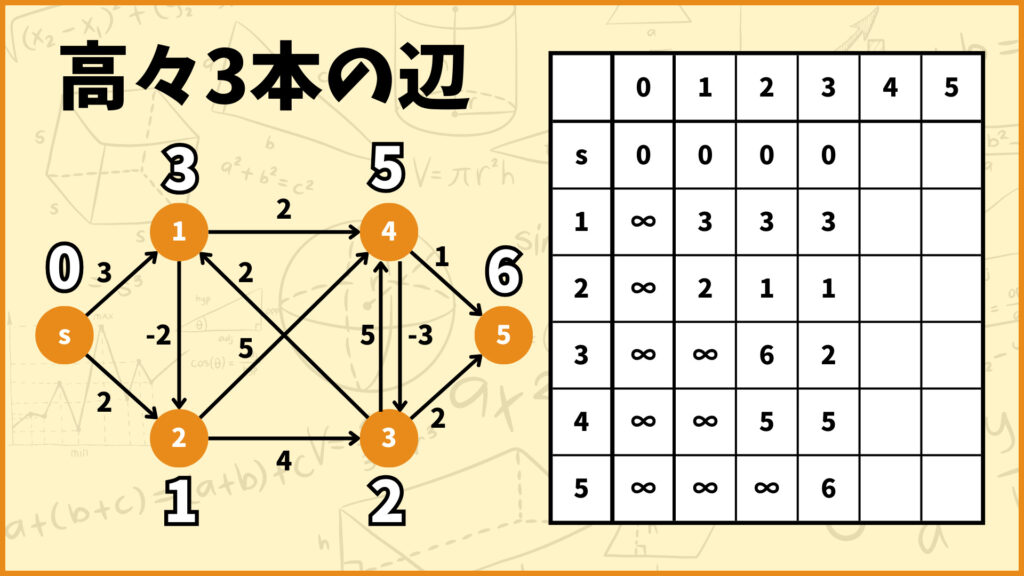
表の更新に伴って各頂点の上に書いてある白黒の数字も更新します。この時点でこれら白黒の数字は
「高々3本の辺を使うときの、始点\(s\)から各頂点への最短距離」
を表していることに注意してください。
STEP.5 高々4本の辺を使う
次に高々4本の辺を使うときの各頂点への最短距離を考えていきましょう。
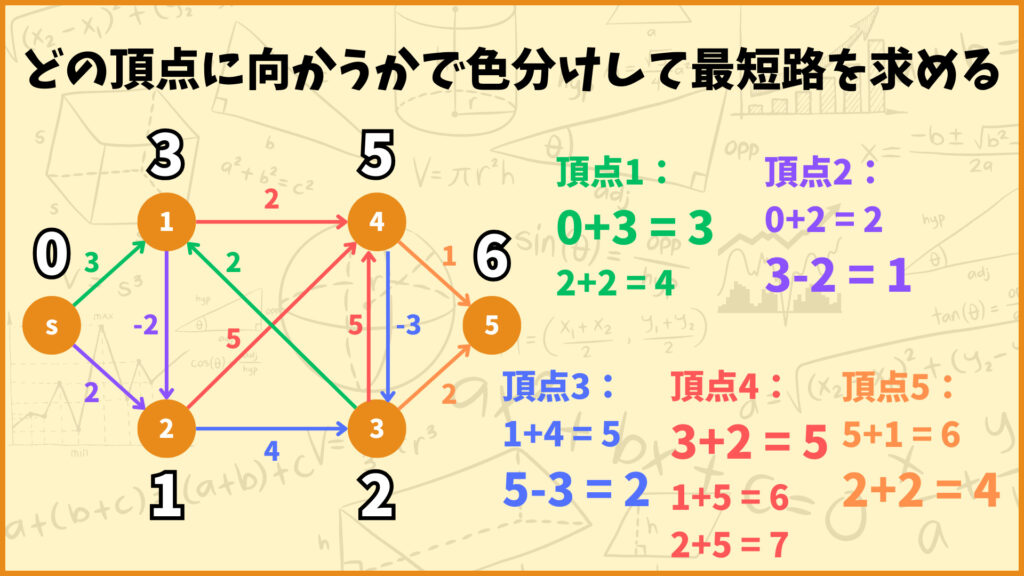
頂点1
頂点1に向かう辺は辺\((s,1),(3,1)\)の2つあります。それぞれの辺を使った場合の最短距離を計算すると以下のようになります。
辺\((s,1)\)を使うときの最短距離:0+3 = 3
辺\((3,1)\)を使うときの最短距離:2+2 = 4
ということで辺\((s,1)\)を使う経路の方が距離が短いことが分かりました。
頂点2
頂点3に向かう辺は辺\((s,2),(1,2)\)の2つあります。それぞれの辺を使った場合の最短距離を計算すると以下のようになります。
辺\((s,2)\)を使うときの最短距離:0+2 = 2
辺\((1,2)\)を使うときの最短距離:3-2 = 1
ということで辺\((1,2)\)を使う経路の方が距離が短いことが分かりました。
頂点3
頂点3に向かう辺は辺\((2,3),(4,3)\)の2つあります。それぞれの辺を使った場合の最短距離を計算すると以下のようになります。
辺\((2,3)\)を使うときの最短距離:1+4 = 5
辺\((4,3)\)を使うときの最短距離:5-3 = 2
ということで辺\((4,3)\)を使う経路の方が距離が短いことが分かりました。
頂点4
頂点4に向かう辺は辺\((1,4),(2,4),(3,4)\)の2つあります。それぞれの辺を使った場合の最短距離を計算すると以下のようになります。
辺\((1,4)\)を使うときの最短距離:3+2 = 5
辺\((2,4)\)を使うときの最短距離:1+5 = 6
辺\((3,4)\)を使うときの最短距離:2+5 = 7
ということで辺\((1,4)\)を使う経路が最短距離だと分かりました。
頂点5
頂点4に向かう辺は辺\((1,4),(2,4),(3,4)\)の2つあります。それぞれの辺を使った場合の最短距離を計算すると以下のようになります。
辺\((4,5)\)を使うときの最短距離:5+1 = 6
辺\((3,5)\)を使うときの最短距離:2+2 = 4
ということで辺\((3,5)\)を使う経路が最短距離だと分かりました。
高々3本の辺を使うときは辺\((4,5)\)を使う方が最短でしたが、最短距離が更新されたので高々4本の辺を使うときは辺\((3,5)\)を使う方が距離が短くなっています。
全ての頂点に対して高々4本の辺を使うときの最短距離が求まったのであの表を更新しましょう。
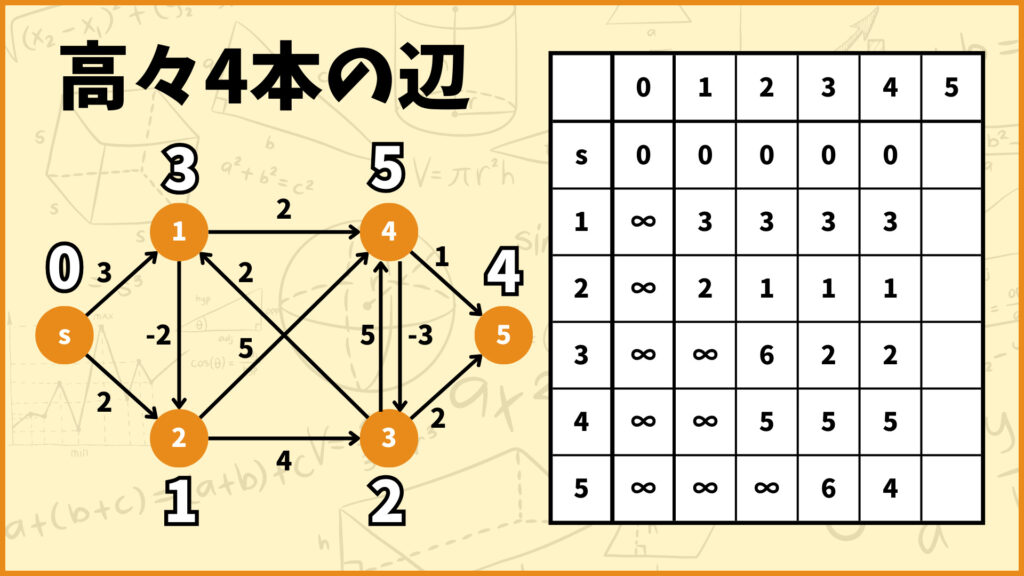
表の更新に伴って各頂点の上に書いてある白黒の数字も更新します。この時点でこれら白黒の数字は
「高々4本の辺を使うときの、始点\(s\)から各頂点への最短距離」
を表していることに注意してください。
STEP.6 高々5本の辺を使う
最後に高々5本の辺を使うときの各頂点への最短距離を考えていきましょう。

頂点1
頂点1に向かう辺は辺\((s,1),(3,1)\)の2つあります。それぞれの辺を使った場合の最短距離を計算すると以下のようになります。
辺\((s,1)\)を使うときの最短距離:0+3 = 3
辺\((3,1)\)を使うときの最短距離:2+2 = 4
ということで辺\((s,1)\)を使う経路の方が距離が短いことが分かりました。
頂点2
頂点3に向かう辺は辺\((s,2),(1,2)\)の2つあります。それぞれの辺を使った場合の最短距離を計算すると以下のようになります。
辺\((s,2)\)を使うときの最短距離:0+2 = 2
辺\((1,2)\)を使うときの最短距離:3-2 = 1
ということで辺\((1,2)\)を使う経路の方が距離が短いことが分かりました。
頂点3
頂点3に向かう辺は辺\((2,3),(4,3)\)の2つあります。それぞれの辺を使った場合の最短距離を計算すると以下のようになります。
辺\((2,3)\)を使うときの最短距離:1+4 = 5
辺\((4,3)\)を使うときの最短距離:5-3 = 2
ということで辺\((4,3)\)を使う経路の方が距離が短いことが分かりました。
頂点4
頂点4に向かう辺は辺\((1,4),(2,4),(3,4)\)の2つあります。それぞれの辺を使った場合の最短距離を計算すると以下のようになります。
辺\((1,4)\)を使うときの最短距離:3+2 = 5
辺\((2,4)\)を使うときの最短距離:1+5 = 6
辺\((3,4)\)を使うときの最短距離:2+5 = 7
ということで辺\((1,4)\)を使う経路が最短距離だと分かりました。
頂点5
頂点4に向かう辺は辺\((1,4),(2,4),(3,4)\)の2つあります。それぞれの辺を使った場合の最短距離を計算すると以下のようになります。
辺\((4,5)\)を使うときの最短距離:5+1 = 6
辺\((3,5)\)を使うときの最短距離:2+2 = 4
ということで辺\((3,5)\)を使う経路が最短距離だと分かりました。
全ての頂点に対して高々5本の辺を使うときの最短距離が求まったのであの表を更新しましょう。
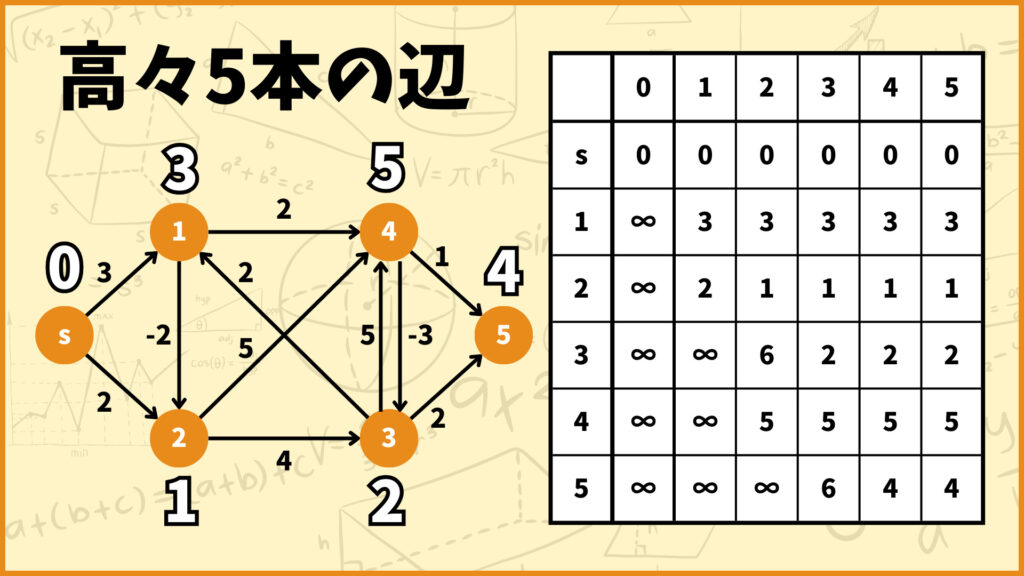
表の更新に伴って各頂点の上に書いてある白黒の数字も更新します。この時点でこれら白黒の数字は
「高々5本の辺を使うときの、始点\(s\)から各頂点への最短距離」
を表していることに注意してください。
高々4本の辺を使うときと高々5本の辺を使うときで最短距離は変わりませんでした。これはどの頂点に関しても、始点\(s\)からの最短距離は高々4本の辺を使うだけで構成できることを表しています。
各頂点への最短距離が求まった
ということでSTEP.1~STEP.6の操作で最短距離を求めることができました。下図に各頂点への最短経路をまとめています。
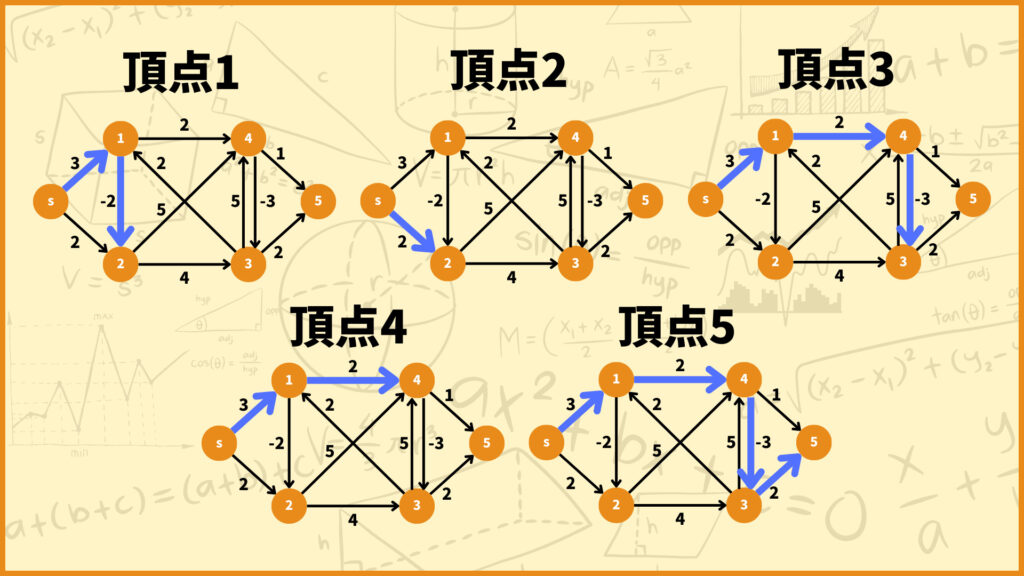
ベルマンフォード法はある条件を満たすグラフに対して、\(n-1\)回の反復で各頂点への最短距離を求めることができます。上のグラフはある条件を満たすので\(6-1=5\)回の反復で最短距離を求めることができました。
その条件とは
負閉路を持たないグラフ
です。
ベルマンフォード法と負閉路
この章では負閉路の説明と、ベルマンフォード法と負閉路の関係を説明したいと思います。
負閉路ってなに?
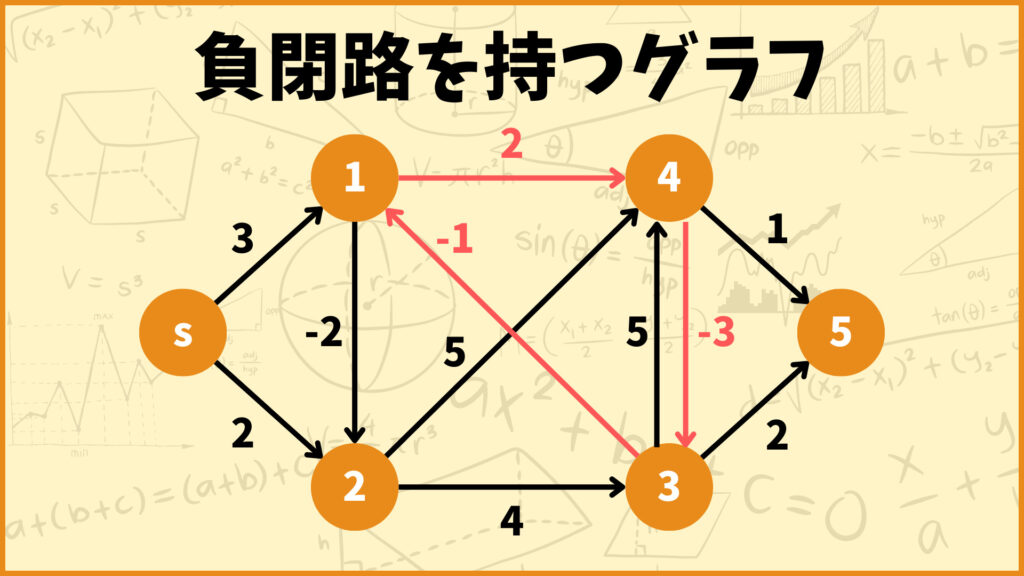
負閉路とは
「重みの合計が負になる閉路」
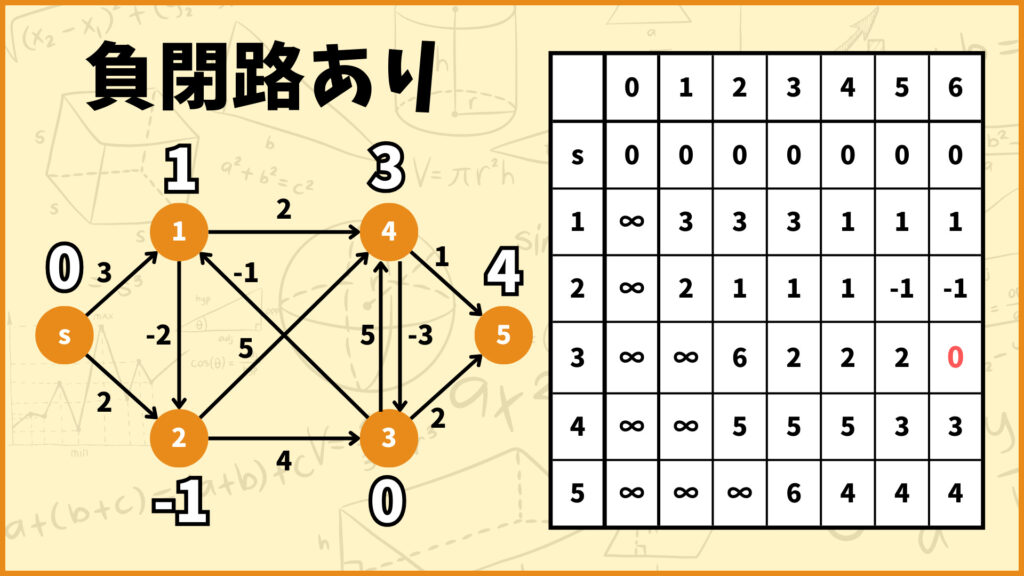
のことです。例えば上のグラフは辺\((1,4),(4,3),(3,1)\)の閉路を持ちますが、これらの辺の重みの合計は
\(2-3-2=-3<0\)
となり負閉路であることが分かります。
実はグラフが負閉路を持ってしまうと最短距離を上手く求めることができないんです。というのも負閉路を何周もすることでどんどん重みの合計は少なくなっていくからです。
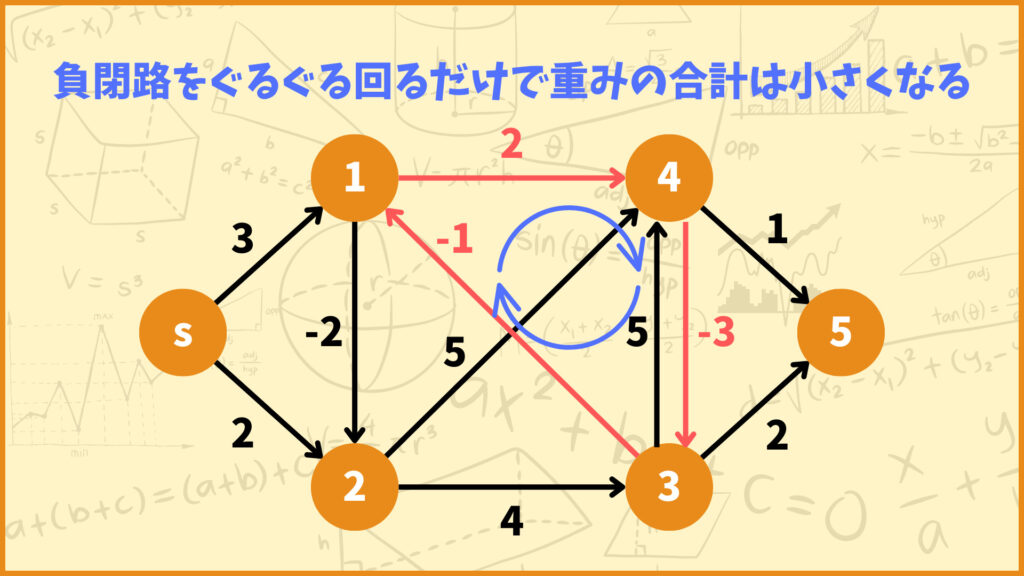
最短経路を求める問題において負閉路は厄介な存在なんですね。
ベルマンフォード法は負閉路を検知できる
ベルマンフォード法を使えば負閉路を検知することができます。
通常ベルマンフォード法では\(n-1\)回の反復で最短距離を求めることができますが、グラフに負閉路が含まれている場合\(n\)回目以降の反復で最短距離がさらに更新されます。(\(n\)はグラフの頂点数)
すなわち\(n\)回目以降の反復で最短距離が更新されるかどうかで負閉路があるかないかを検知することができます。

ここら辺の詳しい話は下の記事で詳しく話しています!
どうして(頂点数-1)回の反復なの?
ベルマンフォード法は負閉路がない場合(頂点数-1)回の反復で始点\(s\)から各頂点までの最短距離を計算できます。なぜ(頂点数-1)回かと言うと、最短経路が最大でも(頂点数-1)本の辺しか持たないからです。

ベルマンフォード法では\(i\)回目の反復で高々\(i\)本の辺を使うときの始点\(s\)から各頂点までの最短距離を求めるので、(頂点数-1)回の反復で計算できるという訳です。
ここら辺の詳しい話は下の記事で説明しています!
おわりに
いかがでしたか。
今回の記事ではベルマンフォード法について解説していきました。
今後もこのようなグラフ理論に関する記事を書いていきます!
最後までこの記事を読んでくれてありがとうございました。