こんにちは!しゅんです!
今回の記事は左右の頂点数が異なる完全2部グラフに対して頂点数が少ない方の頂点集合をすべてカバーする最小重みマッチングついて解説していきます!
マッチングとはグラフ理論という数学の分野で登場する用語で、現実世界の様々な分野で応用できます。
マッチングには色々な種類がありますが、その中でも今回は下図のような左右で頂点数が異なる完全2部グラフの最小重みマッチングを求める問題を整数計画問題として定式化してみたいと思います!
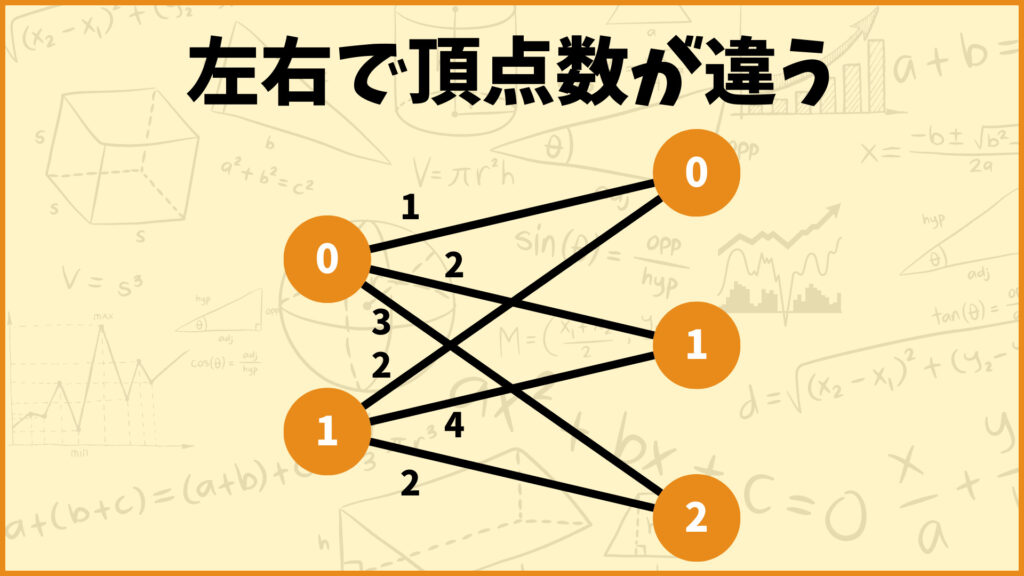
左右で頂点数が違うのでこのグラフには完全マッチングが存在しません。ということで今回は
「頂点数が少ない方の頂点集合を全てカバーするようなマッチングのうち重みの合計が最小となるもの」
を求める方法を考えていきたいと思います。
2部グラフの最小重み完全マッチングについてはこちらの記事で解説しています!
左右で頂点数が同じ完全2部グラフの最小重み完全マッチングの定式化はこちらの記事で解説しています!
それではやっていきましょう!
普段は統計検定2級の記事を書いてたりします。
ぜひ他の記事も読んでみてください!
このブログの簡単な紹介はこちらに書いてあります。
興味があったら見てみてください。
このブログでは経営工学を勉強している現役理系大学生が、経営工学に関することを色々話していきます!
ぼくが経営工学を勉強している中で感じたことや、興味深かったことを皆さんと共有出来たら良いなと思っています。
そもそも経営工学とは何なのでしょうか。Wikipediaによると
経営工学(けいえいこうがく、英: engineering management)は、人・材料・装置・情報・エネルギーを総合したシステムの設計・改善・確立に関する活動である。そのシステムから得られる結果を明示し、予測し、評価するために、工学的な分析・設計の原理・方法とともに、数学、物理および社会科学の専門知識と経験を利用する。
引用元 : 経営工学 – Wikipedia
長々と書いてありますが、要は経営、経済の課題を理系的な観点から解決する学問です。
具体例を使って考える
それではまず以下の完全2部グラフについて最小重みマッチングを考えてみましょう。
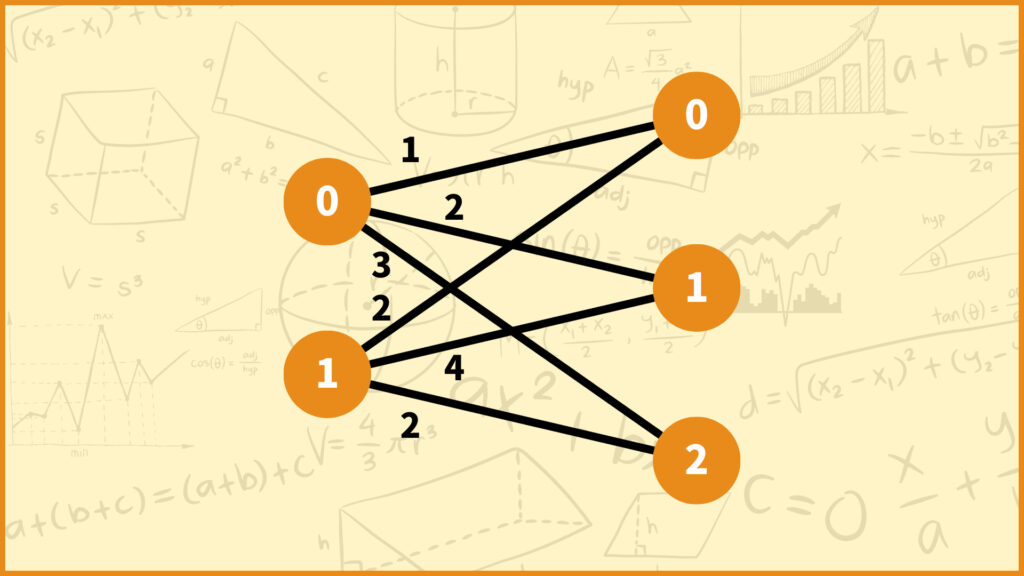
このグラフは頂点数がそれぞれ左側が2つ、右側が3つある完全2部グラフです。各辺には重みが与えられており、例えば辺(0,1)の重みは2です。
整数計画問題として定式化するために「変数」、「目的関数」、「制約条件」の3つを考えていきましょう。
変数の設定
まず最初に変数の設定をしていきましょう。頂点\(i\)を左側の頂点、頂点\(j\)を右側の頂点とするとき、今回は以下の変数\(x_{ij}\)を使います。
\(x_{ij}= \left\{\begin{array}{lr} 1 \;\;\; \text{辺}(i,j)\text{を採用する} \\ 0 \;\;\; \text{辺}(i,j)\text{を採用しない} \end{array} \right.\)
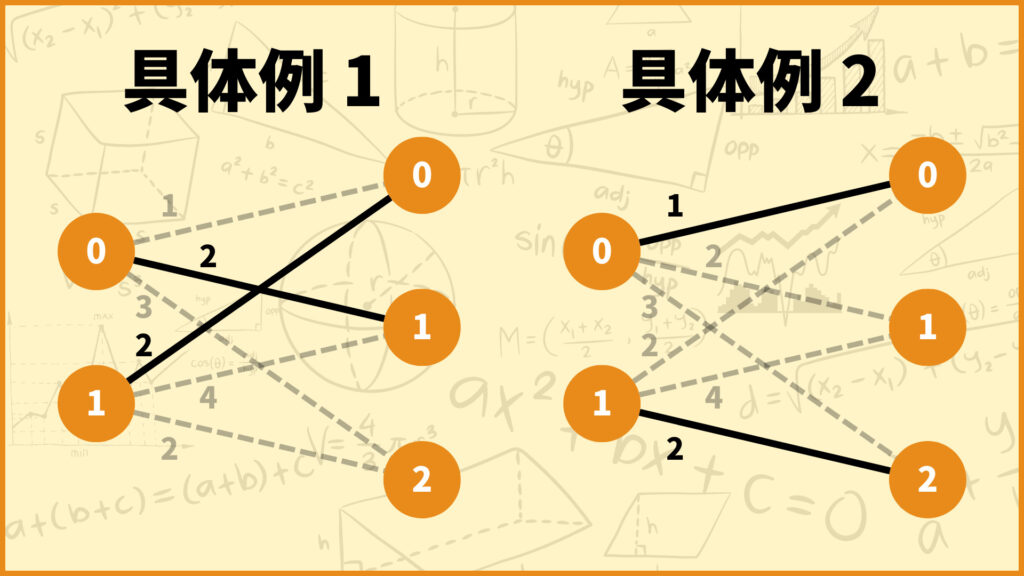
例えば上の具体例だと各変数\(x_{ij}\)は以下のようになります。
\(x_{01}=x_{10}=1\)
\(x_{00}=0\)
\(x_{02}=0\)
\(x_{11}=0\)
\(x_{12}=0\)
\(x_{00}=x_{12}=1\)
\(x_{01}=0\)
\(x_{02}=0\)
\(x_{10}=0\)
\(x_{11}=0\)
目的関数の設定
次に目的関数を設定します。今回は最小重みマッチングを求めたいので、採用した辺の重みの合計を目的関数とします。これを変数\(x_{ij}\)を使って表すと以下のようになります。
\(x_{00}+2x_{01}+3x_{02}+2x_{10}+4x_{11}+2x_{12}\)
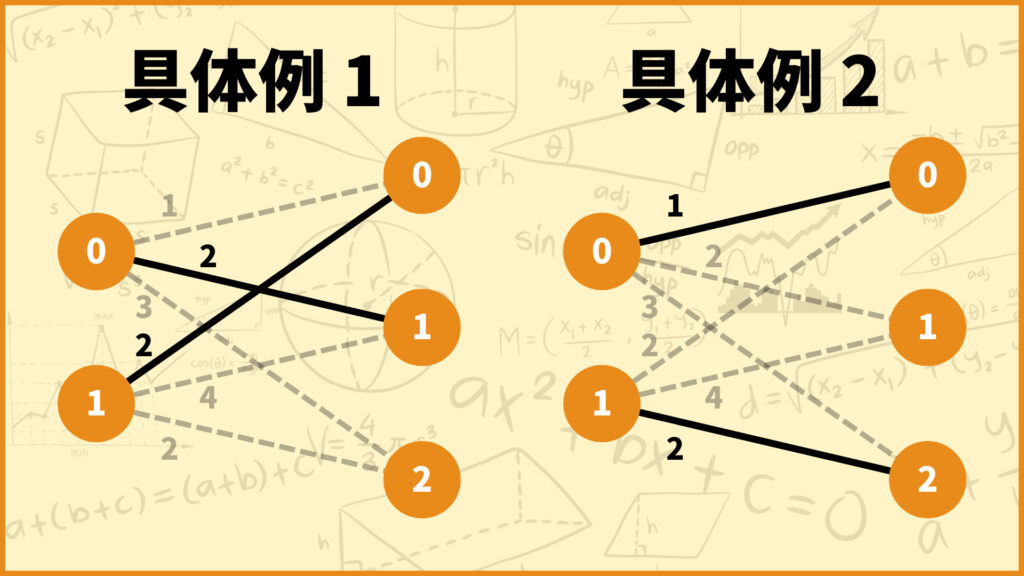
例えば上の具体例だと目的関数はそれぞれ以下のようになります。
\((1\times 0)+(2\times 1) + (3\times 0)+(2\times 1)+(4\times 0)+(2\times 0)\)
\(=2+2=4\)
\((1\times 1)+(2\times 0) + (3\times 0)+(2\times 0)+(4\times 0)+(2\times 1)\)
\(=1+2=3\)
マッチングとして採用されない辺\((i,j)\)の変数\(x_{ij}\)は0になるので、目的関数のその部分は0となります。そのため最終的に足される値はマッチングとして採用された辺の重みとなる訳です。
制約条件の設定1 : 左側の頂点
それでは最後に制約条件を設定しましょう。まず最初に左側の頂点0について考えてみましょう。
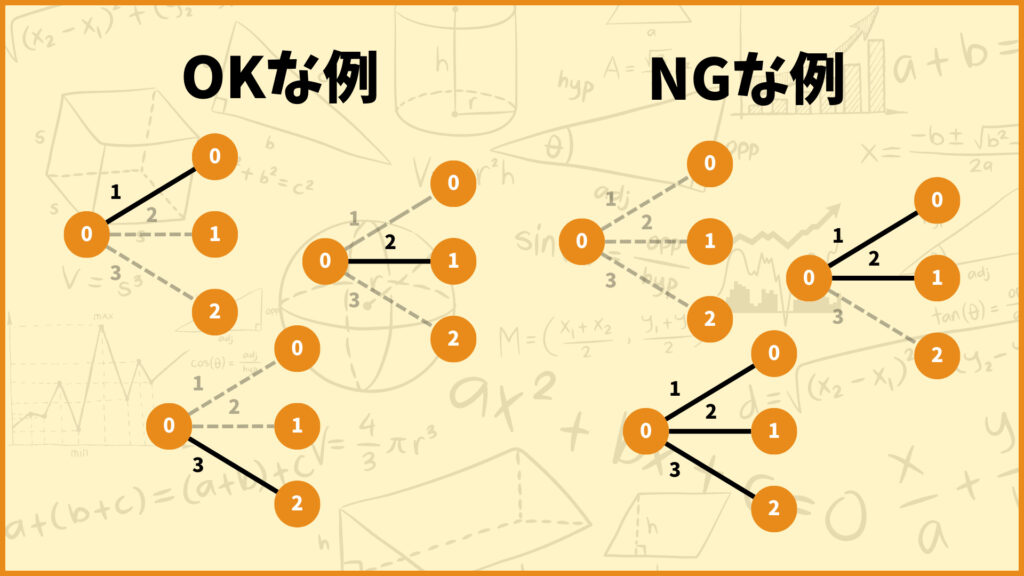
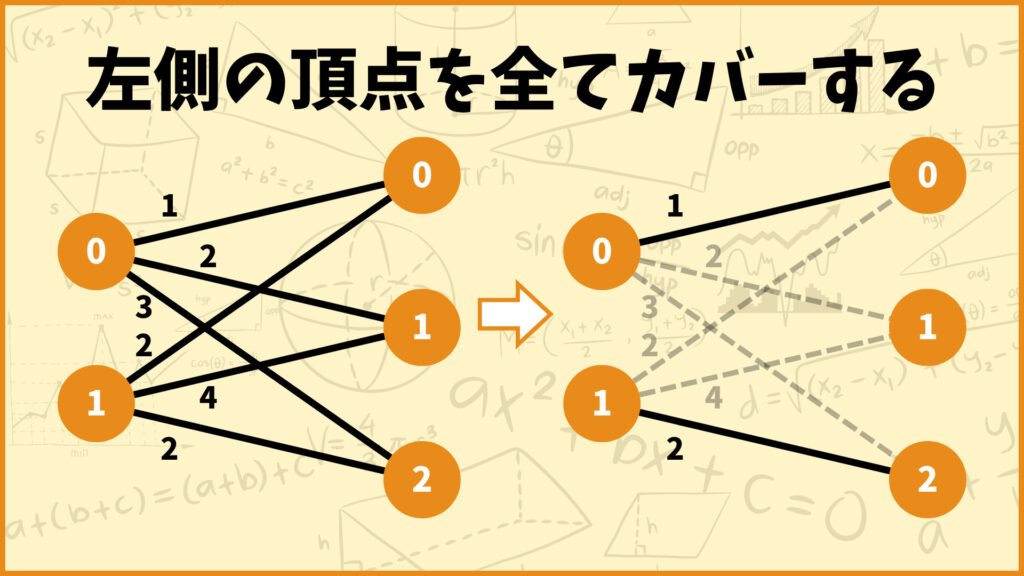
左側の頂点はすべてカバーする必要があるので、左側の頂点0は右側のいずれか1つの頂点と結ばれる必要があります。上の図の左側の例がOKな例です。
一方で例えばどの右側の頂点とも結ばれない、頂点0が2つの頂点と結ばれている場合はマッチングにはなりません。このNGな例を作らないように制約条件を設定する必要があります。
左側の頂点0に関する変数は\(x_{00},x_{01},x_{02}\)の3つですが、これらのうちいずれか1つが1になって残り2つが0になればOKです。ということで左側の頂点0に関する制約条件は以下のようになります。
左側の頂点0に関する制約:
\(x_{00}+x_{01}+x_{02}=1\)
またこの条件は左側の頂点1に対しても成立する必要があります。
左側の頂点1に関する制約:
\(x_{10}+x_{11}+x_{12}=1\)
制約条件の設定2 : 右側の頂点
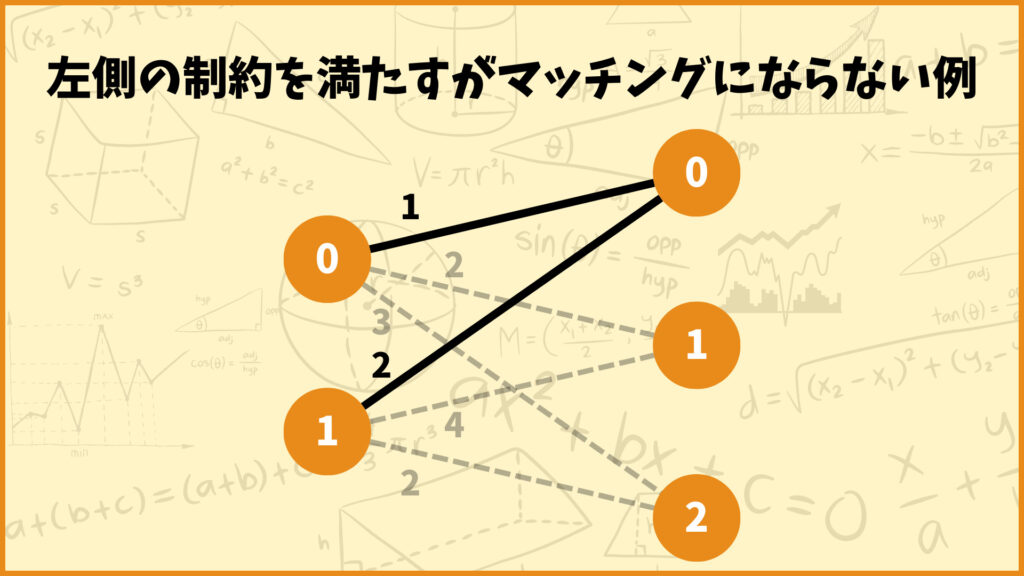
次に右側の頂点について考えましょう。実は左側の頂点に関する制約を考えただけでは条件が足りないんです。上の図は左側の頂点に関する制約条件を全て満たすあるグラフです。
確かにこのグラフの左側の頂点を見るとちゃんと1つの辺と接続していますね。しかし右側の頂点を見てみると、頂点0は2つの辺と接続しているので、これではマッチングにはなりません。
そういった理由で右側の頂点に関しても制約条件を付け足す必要があります。しかしここで重要なのは、
右側の頂点の中には左側の頂点と結ばれないものが必ず存在する
ということです。まあ左右で頂点数が違うので当たり前ですね。そのため左側の頂点に関する制約条件と同じようにすることはできません。
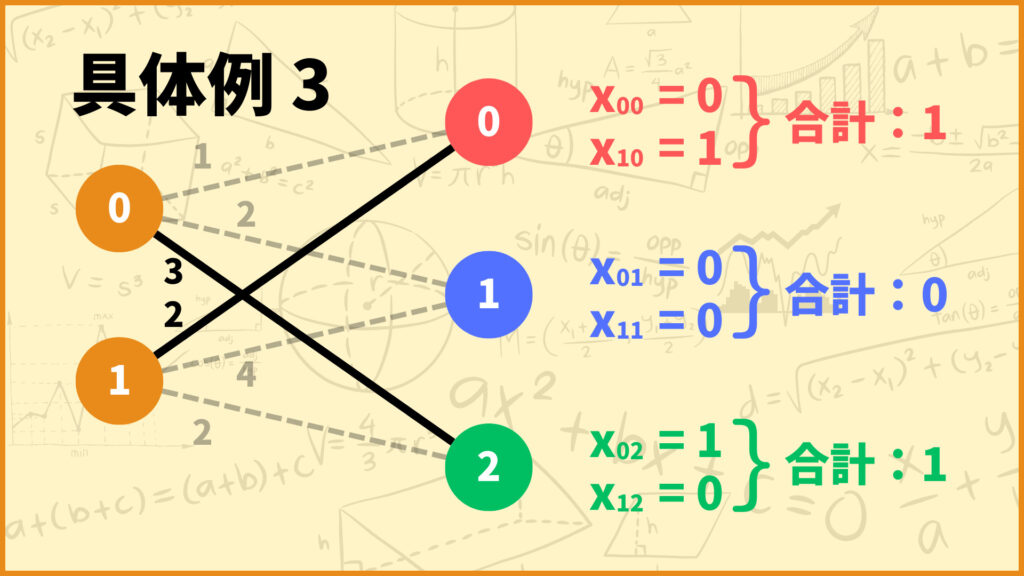
上の具体例3を見てみましょう。上の例は左側の頂点を全てカバーするマッチングとなっています。注目すべきは右側の各頂点に対してその頂点に関する変数の値の合計がどうなっているかです。
頂点0及び頂点2はそれぞれ1本の辺と接続しているので変数の値の合計が1となっていますが、頂点1は1本も辺と接続していないので変数の値の合計は0となります。このように右側の頂点に関しては\(x_{0i}+x_{1i}\)が0になるものと1になるものが両方存在します。
ということで制約条件は\(=1\)ではなく\(\leq 1\)にします。
右側の頂点0に関する制約:
\(x_{00}+x_{10} \leq 1\)
右側の頂点1に関する制約:
\(x_{01}+x_{11} \leq 1\)
右側の頂点2に関する制約:
\(x_{02}+x_{12} \leq 1\)
整数計画問題としてまとめる
それでは最後にここまで話してきたことをまとめて整数計画問題として定式化しましょう。
定式化1:
\( \min \;\;\; x_{00}+2x_{01}+3x_{02}+2x_{10}+4x_{11}+2x_{12}\)
\(\; \text{s.t.} \;\;\;\;x_{00}+x_{01}+x_{02}=1\)
\(\;\;\;\;\;\;\;\;\;\;x_{10}+x_{11}+x_{12}=1\)
\(\;\;\;\;\;\;\;\;\;\;x_{00}+x_{10} \leq 1\)
\(\;\;\;\;\;\;\;\;\;\;x_{01}+x_{11} \leq 1\)
\(\;\;\;\;\;\;\;\;\;\;x_{02}+x_{12} \leq 1\)
\(\;\;\;\;\;\;\;\;\;\;x_{ij}\in \{0,1\}\;\;\;\;(i = 0,1\;j = 0,1,2)\)
これで一応定式化はできたんですけど結構見づらいですよね。ということでいくつか文字を導入してもう少し簡潔に表記したいと思います。
もう少し簡潔に表す

まず辺\((i,j)\)の重みを\(w_{ij}\)と表します。例えば辺\((0,0)\)の重みは1なので\(w_{00}=1\)となります。これを使って目的関数を書き換えると以下のように表すことができます。
\(\sum\limits_{i=0}^1 \sum\limits_{j=0}^2 w_{ij}x_{ij}\)
さらに制約条件も\(\sum\)を使うと以下のように表せます。
左側の頂点:
\(\sum\limits_{j=0}^2 x_{ij}=1 \;\;\;\; (i = 0,1)\)
右側の頂点:
\(\sum\limits_{i=0}^1 x_{ij} \leq 1 \;\;\;\; (j = 0,1,2)\)
ということでこれらをまとめると最小重み完全マッチングを以下のように整数計画問題として定式化できます。
定式化2:
\(\min \;\;\; \sum\limits_{i=0}^1 \sum\limits_{j=0}^2 w_{ij}x_{ij}\)
\(\;\text{s.t.}\;\;\;\sum\limits_{j=0}^2 x_{ij}=1 \;\;\;\; (i = 0,1)\)
\(\;\;\;\;\;\;\;\;\;\sum\limits_{i=0}^1 x_{ij} \leq 1 \;\;\;\; (j = 0,1,2)\)
\(\;\;\;\;\;\;\;\;\; x_{ij} \in \{0,1\} \;\;(i=0,1 \; j=0,1,2)\)
より一般的に考える
それではこれまでの具体例を踏まえてより一般的な完全2部グラフの最小重み完全マッチングを定式化してみましょう。
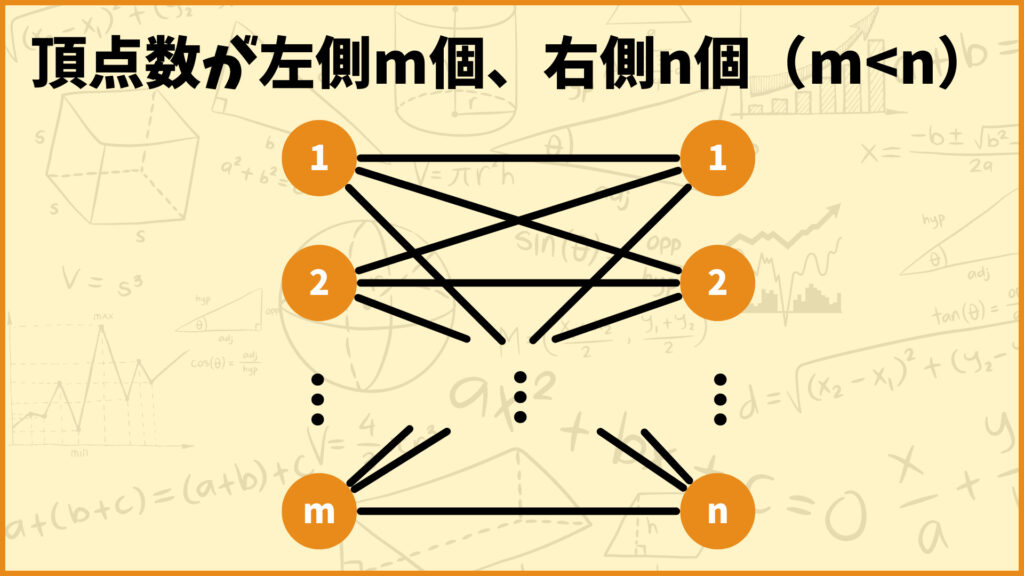
上のグラフは左側の頂点が\(m\)個、右側の頂点が\(n\)個、合計\(m+n\)個の頂点を持つ完全2部グラフです。(\(m>n\))
このグラフに対して、左側の\(m\)個の頂点を全てカバーするマッチングの中で重みの合計が最小となるものを求める問題を整数計画問題として定式化してみましょう。
変数の設定
まず最初に定式化するために必要なパラメータや変数を設定しましょう。まず辺\((i,j)\)の重みを\(w_{ij}\)とします。(頂点\(i\)は左側の頂点、頂点\(j\)は右側の頂点)また辺\((i,j)\)をマッチングとして採用するなら1、そうでないなら0を取るような変数を\(x_{ij}\)とします。
\(w_{ij}\) : 辺\((i,j)\)の重み
\(x_{ij}\in\{0,1\}\) : 辺\((i,j)\)を採用するなら1、そうでないなら0
目的関数の設定
次に目的関数の設定をしましょう。具体例の時は頂点がそれぞれ左側が2個、右側が3個でしたが、一般的なグラフでは頂点が左側に\(m\)個、右側に\(n\)個あるのでそこだけ変えれば大丈夫です。
\( \sum\limits_{i=1}^m \sum\limits_{j=1}^n w_{ij}x_{ij}\)
制約条件の設定
最後に制約条件を設定します。具体例の時は\(i=0,1,2 \; j=0,1,2\)のときを話していましたが、頂点数が左側\(m\)個、右側\(n\)個なので\(i=1,2,…,m \; j=1,2,…,n\)とすれば良いです。
左側の頂点:
\(\sum\limits_{j=1}^n x_{ij}=1 \;\;\;\; (i = 1,2,…,m)\)
右側の頂点:
\(\sum\limits_{i=1}^m x_{ij} \leq 1 \;\;\;\; (j = 1,2,…,n)\)
整数計画問題としてまとめる
最後にこれらをまとめて整数計画問題として定式化しましょう。
定式化:
\(\min \;\;\; \sum\limits_{i=1}^m \sum\limits_{j=1}^n w_{ij}x_{ij}\)
\(\;\text{s.t.}\;\;\;\sum\limits_{j=1}^n x_{ij}=1 \;\;\;\; (i = 1,2,…,m)\)
\(\;\;\;\;\;\;\;\;\;\sum\limits_{i=1}^m x_{ij} \leq 1 \;\;\;\; (j = 1,2,…,n)\)
\(\;\;\;\;\;\;\;\;\; x_{ij} \in \{0,1\} \;\;(i=1,2,…,m \; j=1,2,…,n)\)
次回の記事では定式化した整数計画問題をpythonで表現して実際に問題を解いてみたいと思います!
次回の記事はこちらから!
おわりに
いかがでしたか。
今回の記事では2部グラフの最小重み完全マッチングについて解説していきました。
今後もこのようなグラフ理論に関する記事を書いていきます!
最後までこの記事を読んでくれてありがとうございました。