こんにちは!しゅんです!
今回の記事は2部グラフの最小重み完全マッチングついて解説していきます!
マッチングとはグラフ理論という数学の分野で登場する用語で、現実世界の様々な分野で応用できます。
マッチングには色々な種類がありますが、その中でも今回は完全グラフじゃない2部グラフの最小重み完全マッチングを求める問題を整数計画問題として定式化してみたいと思います!
2部グラフの最小重み完全マッチングについてはこちらの記事で解説しています!
完全2部グラフの最小重み完全マッチングの定式化はこちらの記事で解説しています!
それではやっていきましょう!
普段は統計検定2級の記事を書いてたりします。
ぜひ他の記事も読んでみてください!
このブログの簡単な紹介はこちらに書いてあります。
興味があったら見てみてください。
このブログでは経営工学を勉強している現役理系大学生が、経営工学に関することを色々話していきます!
ぼくが経営工学を勉強している中で感じたことや、興味深かったことを皆さんと共有出来たら良いなと思っています。
そもそも経営工学とは何なのでしょうか。Wikipediaによると
経営工学(けいえいこうがく、英: engineering management)は、人・材料・装置・情報・エネルギーを総合したシステムの設計・改善・確立に関する活動である。そのシステムから得られる結果を明示し、予測し、評価するために、工学的な分析・設計の原理・方法とともに、数学、物理および社会科学の専門知識と経験を利用する。
引用元 : 経営工学 – Wikipedia
長々と書いてありますが、要は経営、経済の課題を理系的な観点から解決する学問です。
2パターンの定式化を考える
今回は2パターンの定式化を考えたいと思います。1つ目は「辺集合を中心に考える方法」で、2つ目は「辺の重みをめっちゃ大きくする方法」です。
この記事では「辺の重みをめっちゃ大きくする方法」について解説したいと思います!
「辺集合を中心に考える方法」についてはこちらの記事で解説しています!
定式化のイメージ
それではまず最初に解き方のイメージを説明したいと思います。ポイントは
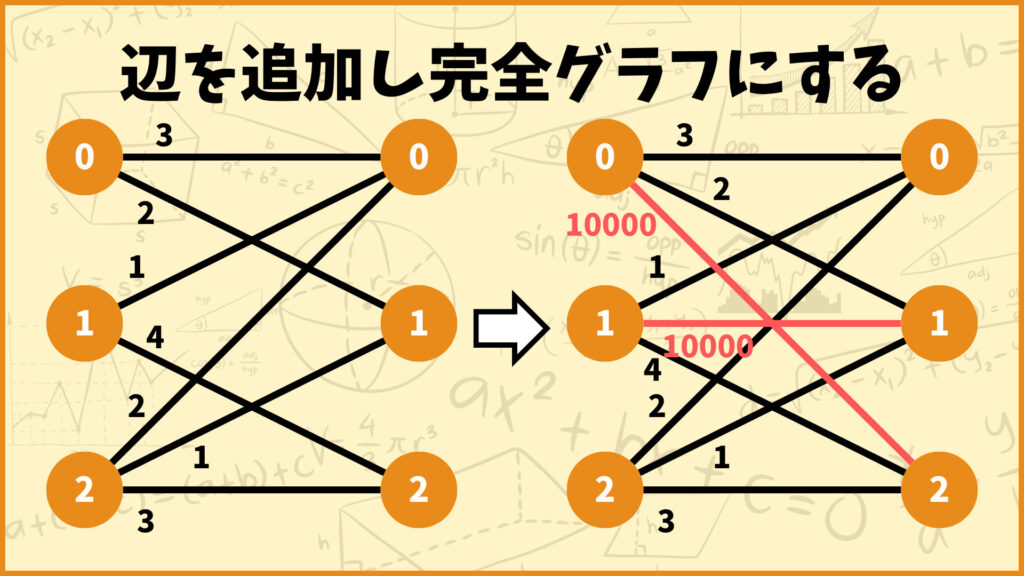
「辺を追加して完全グラフにする」
ということです。例えば上図の左側の2部グラフを見てください。この2部グラフは辺\((0,2)\)と辺\((1,1)\)がないので完全2部グラフではありません。
そこで右側のグラフのように無理やり辺を追加して完全2部グラフにすることを考えます。なぜ完全2部グラフにするかというと、前回の記事で説明したように、完全2部グラフの最小重み完全マッチングは簡単に整数計画問題として定式化できるからです。
完全2部グラフの最小重み完全マッチングについてはこちらの記事で解説しています!
そしてもう1つのポイントは
「追加した辺の重みをめっちゃ大きくする」
ということです。辺を追加したは良いものの、結局この追加した辺は使ってほしくないんです。
もし追加した辺が最小重み完全マッチングの辺として採用されてしまったら、元のグラフの最小重み完全マッチングではなくなってしまいますよね。
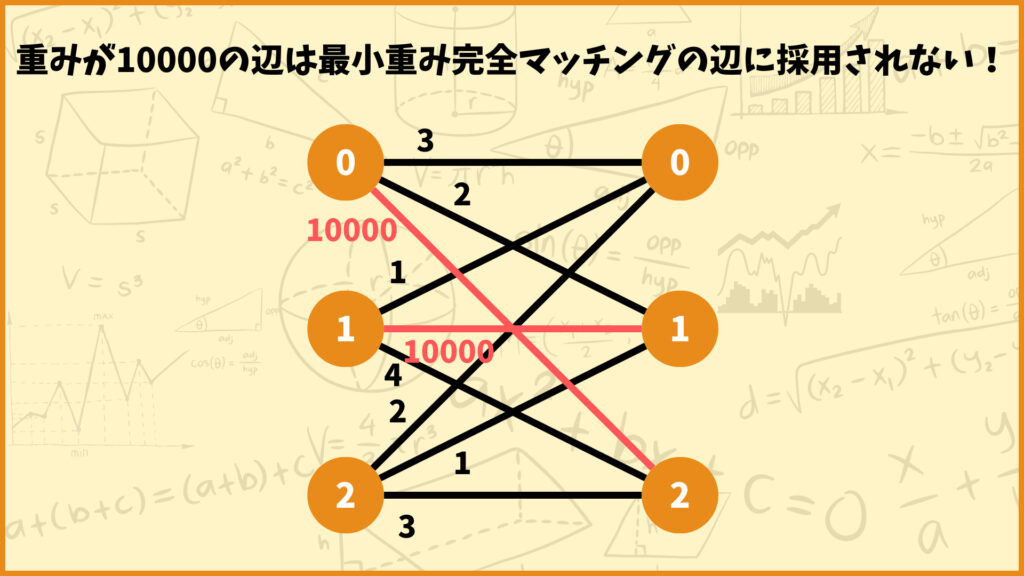
これを解決するために追加した辺の重みをめっちゃ大きくします。例えば上の例では辺の重みを10000にしています。こうすることで最小重み完全マッチングを求める際に追加した辺が選ばれなくなるという訳です。
もう少し詳しく説明すると、追加した重み10000の辺が採用されないのは、元のグラフで完全マッチングが存在する場合です。
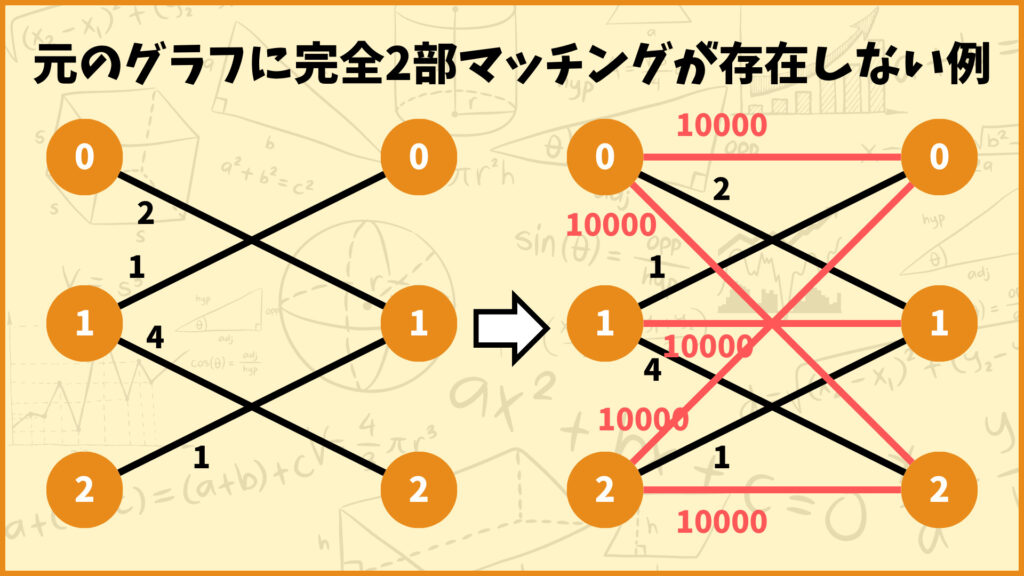
もし元のグラフに完全2部マッチングが存在しないのに、辺を追加して完全2部グラフにしてまったら、辺の重みをどれだけ重くしても追加した辺を採用しちゃいます。
※ちなみに2部グラフに完全マッチングが存在するかどうかはHallの結婚定理というものを使って判断できます。
ということでここまでの議論から、今求めたい問題を完全2部グラフの最小重み完全マッチングを求める問題に変えることができました。あとは完全2部グラフの最小重み完全マッチングを求める問題を整数計画問題として定式化すればOKです。
これは前回の記事で説明しているので、この記事では簡単に説明したいと思います。
完全2部グラフの最小重み完全マッチングについてはこちらの記事で解説しています!
整数計画問題として定式化する
それでは完全2部グラフの最小重み完全マッチング問題を整数計画問題として定式化してみましょう。
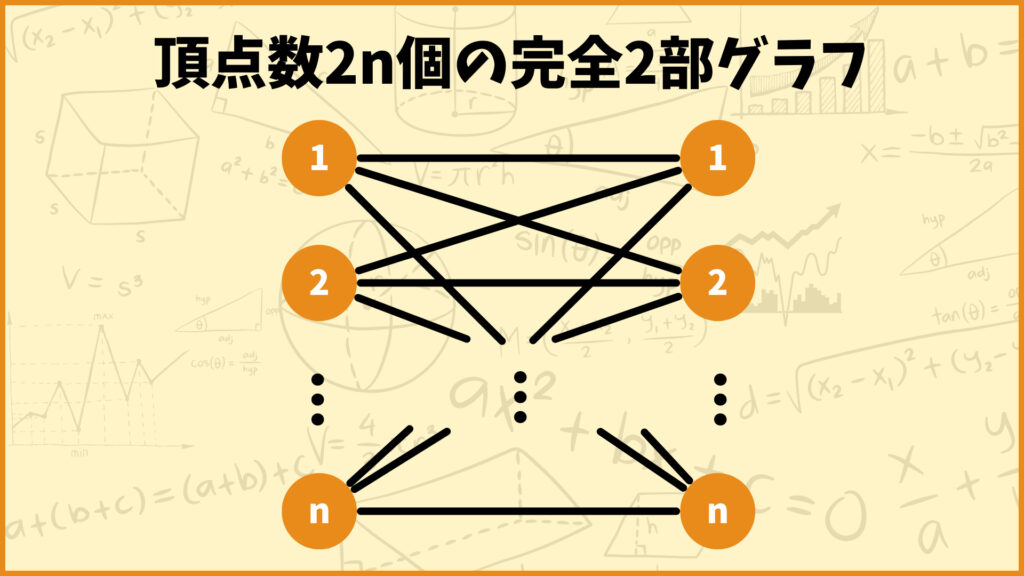
上のグラフは左側の頂点が\(n\)個、右側の頂点が\(n\)個、合計2\(n\)個の頂点を持つ完全2部グラフです。この完全2部グラフの最小重み完全マッチングを求める整数計画問題を定式化します。
変数の設定
まず最初に定式化するために必要なパラメータや変数を設定しましょう。まず辺\((i,j)\)の重みを\(w_{ij}\)とします。また辺\((i,j)\)をマッチングとして採用するなら1、そうでないなら0を取るような変数を\(x_{ij}\)とします。
\(w_{ij}\) : 辺\((i,j)\)の重み
\(x_{ij}\in\{0,1\}\) : 辺\((i,j)\)を採用するなら1、そうでないなら0
目的関数の設定
次に目的関数の設定をしましょう。
\( \sum\limits_{i=1}^n\sum\limits_{j=1}^n w_{ij}x_{ij}\)
制約条件の設定
最後に制約条件を設定します。頂点数が\(n\)個なので\(i=1,2,…,n \; j=1,2,…,n\)とすれば良いです。
左側の頂点:
\(\sum\limits_{j=1}^n x_{ij}=1 \;\;\;\; (i = 1,2,…,n)\)
右側の頂点:
\(\sum\limits_{i=1}^n x_{ij}=1 \;\;\;\; (j = 1,2,…,n)\)
整数計画問題としてまとめる
最後にこれらをまとめて整数計画問題として定式化しましょう。
定式化:
\(\min \;\;\; \sum\limits_{i=1}^n \sum\limits_{j=1}^n w_{ij}x_{ij}\)
\(\;\text{s.t.}\;\;\;\sum\limits_{j=1}^n x_{ij}=1 \;\;\;\; (i = 1,2,…,n)\)
\(\;\;\;\;\;\;\;\;\;\sum\limits_{i=1}^n x_{ij}=1 \;\;\;\; (j = 1,2,…,n)\)
\(\;\;\;\;\;\;\;\;\; x_{ij} \in \{0,1\} \;\;(i=1,2,…,n \; j=1,2,…,n)\)
次回の記事では今回定式化した整数計画問題をpythonで表現して実際に問題を解いてみたいと思います!
次回の記事はこちらから!
おわりに
いかがでしたか。
今回の記事では完全グラフじゃない2部グラフの最小重み完全マッチングについて解説していきました。
今後もこのような数理最適化に関する記事を書いていきます!
最後までこの記事を読んでくれてありがとうございました。