こんにちは!しゅんです!
この記事では最短経路問題について説明します。
最短経路問題はある地点からある地点までの最短距離を求める問題です。
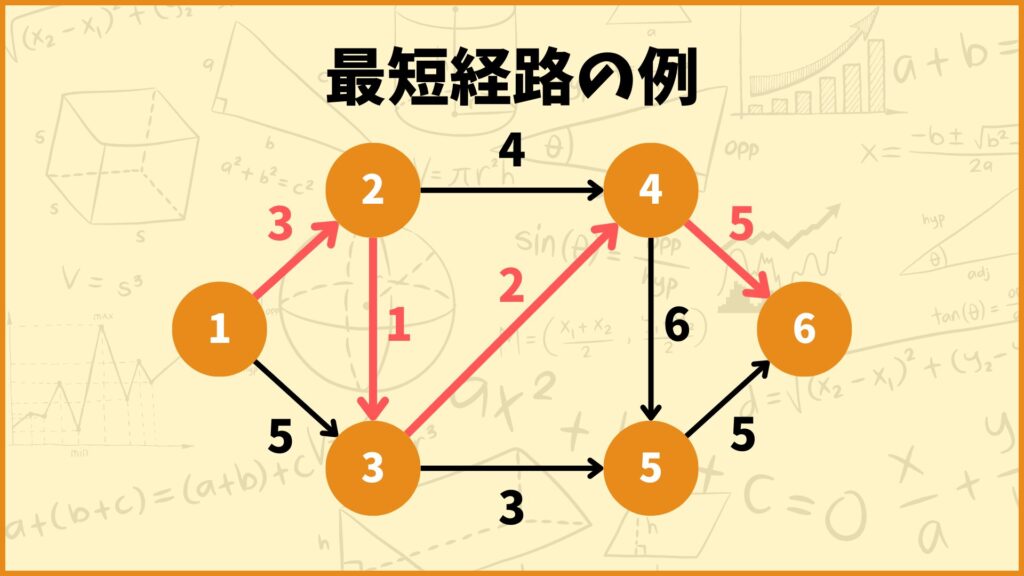
この記事では最短経路問題を整数計画問題として定式化してpythonで解く方法を解説したいと思います。
それではやっていきましょう!
普段は組合せ最適化の記事を書いてたりします。
ぜひ他の記事も読んでみてください!
このブログの簡単な紹介はこちらに書いてあります。
興味があったら見てみてください。
このブログでは経営工学を勉強している現役理系大学生が、経営工学に関することを色々話していきます!
ぼくが経営工学を勉強している中で感じたことや、興味深かったことを皆さんと共有出来たら良いなと思っています。
そもそも経営工学とは何なのでしょうか。Wikipediaによると
経営工学(けいえいこうがく、英: engineering management)は、人・材料・装置・情報・エネルギーを総合したシステムの設計・改善・確立に関する活動である。そのシステムから得られる結果を明示し、予測し、評価するために、工学的な分析・設計の原理・方法とともに、数学、物理および社会科学の専門知識と経験を利用する。
引用元 : 経営工学 – Wikipedia
長々と書いてありますが、要は経営、経済の課題を理系的な観点から解決する学問です。
問題設定
まず最初に今回解きたい問題を設定しましょう。
問題設定:
有向グラフ\(G = (V,E)\)と各辺\((i,j) \in E\)の重み\(w_{ij}(>0)\)がと始点\(s \in V\)、終点\(t \in V\)が与えられる。このとき始点\(s\)から終点\(t\)までの経路の中で経路中の辺の重みの合計が最小となるものを見つけたい。
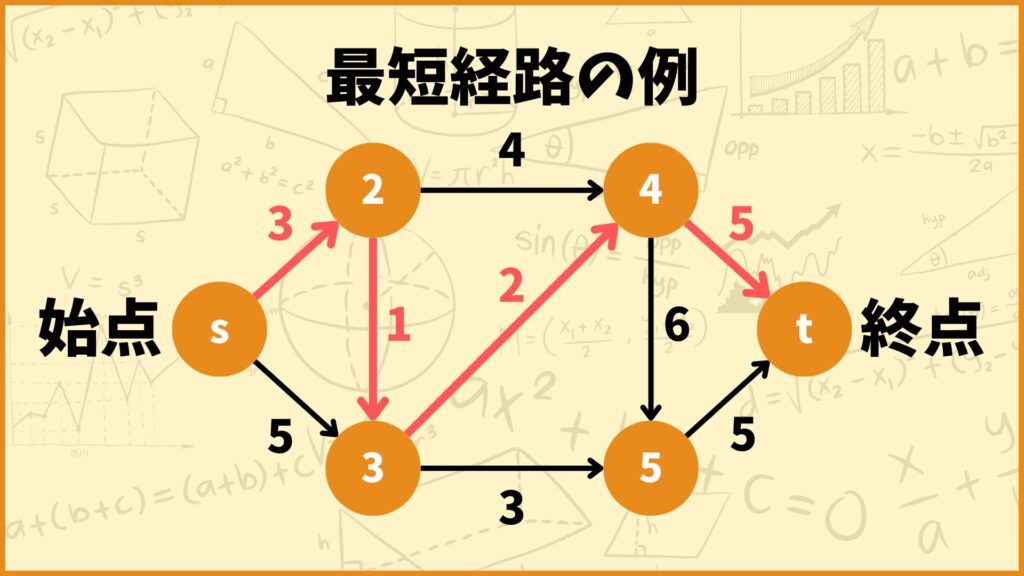
問題を簡単にするために始点に向かう辺、終点から出る辺は無いとします。
例えば上の図の例で言うと始点\(s\)から終点\(t\)までの最短経路は
\(s \to 2 \to 3 \to 4 \to t\)
となります。このとき辺の重みの合計は
\(w_{s2} + w_{23} + w_{34} + w_{4t} = 3+1+2+5 = 11\)
となります。このような問題を解く方法を考えてみます。
整数計画問題として定式化
それではまず最初に整数計画問題として定式化する方法を説明します。「記号の定義」、「目的関数の設定」、「制約条件の設定」の3つに分けてそれぞれ説明したいと思います。
記号の定義
パラメータ:
\(V\) : 頂点集合
\(E\) : 辺集合
\(w_{ij}\) : 辺\((i,j)\)の重み
変数:
\(x_{ij} \in \{0,1\}\) : 辺\((i,j)\)を採用するなら1、そうでないなら0を取る0-1変数
パラメータとして頂点集合\(V\)、辺集合\(E\)、辺\((i,j)\)の重みを設定します。

上の例で言うと
\(V = \{1,2,3,4,5,6\}\)
\(E = \{(1,2),(1,3),(2,3),(2,4),(3,4),(3,5),(4,5),(4,6),(5,6)\}\)
となります。めんどくさいので\(w_{ij}\)は全部書きませんが、例えば
\(w_{12} = 3\)
\(w_{34} = 2\)
\(w_{45} = 6\)
となります。変数は辺\((i,j)\)を採用するなら1、そうでないなら0を取る0-1変数\(x_{ij}\)を使います。上の例で言うと
\(x_{12} = x_{23} = x_{34} = x_{46}=1\)
となります。
始点が頂点1、終点が頂点6だと考えてください。
目的関数の設定
目的関数:
\(\sum\limits_{(i,j) \in E}w_{ij}x_{ij}\)
今回の問題の目的は
「経路中の辺の重みの合計を最小にする」
というものです。

上の赤矢印の経路でいうと
\(x_{12} = x_{23} = x_{34} = x_{46}=1\)
となるので目的関数値は
\(\sum\limits_{(i,j) \in E}w_{ij}x_{ij} = w_{12} + w_{23} + w_{34} + w_{46} = 11\)
となり、これは上の経路中の辺の重みの合計となっていますね。今回はこれが最小となる場合を求めたいので問題を\(\text{minimize}\)に設定します。
目的関数を最小化:
\(\min \;\; \sum\limits_{(i,j) \in E}w_{ij}x_{ij}\)
制約条件の設定
制約条件:
\(\sum\limits_{j \in V,(s,j) \in E}x_{sj} = 1\) → ①
\(\sum\limits_{i \in V,(i,t) \in E}x_{it} = 1\) → ②
\(\sum\limits_{i \in V,(i,j) \in E}x_{ij}-\sum\limits_{k \in V, (j,k) \in E}x_{jk} = 0 \;\;\; (\forall j \in V/\{s,t\})\) → ③
1つずつ解説していきます。
1つ目の制約
\(\sum\limits_{j \in V,(s,j) \in E}x_{sj} = 1\)
1つ目の制約は
「始点から出る辺を必ず1つだけ選ぶ」
ということを表しています。\(s\)が始点だと思ってください。\(\sum\limits_{j \in V, (s,j) \in E}\)は\(V\)中の頂点\(j\)で\((s,j)\)が\(E\)中の辺であるものを全て足し算するということを表しています。
つまり始点\(s\)から出る辺に対応する変数を全部足すということを表しています。
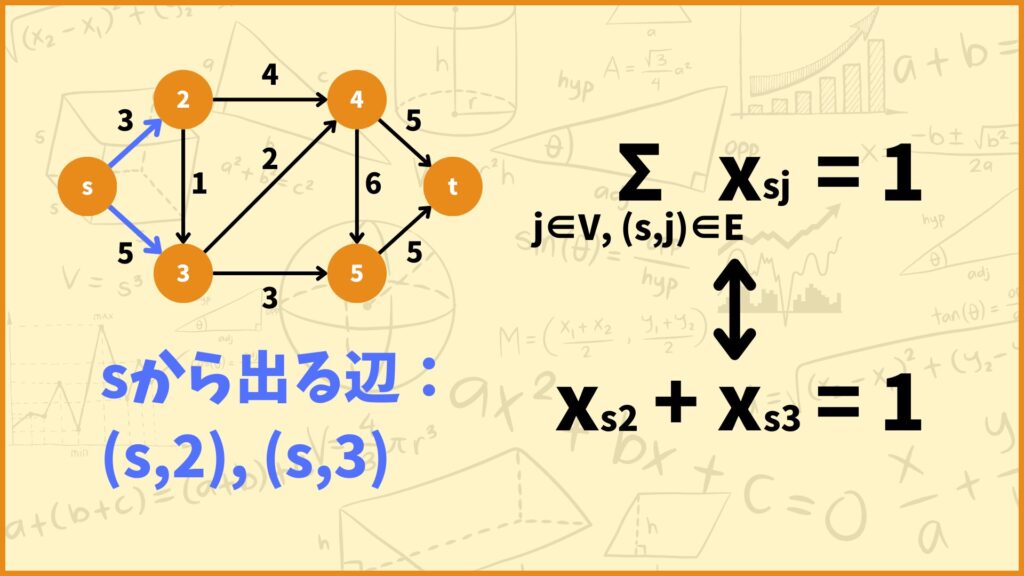
例えば上の例を見てみましょう。始点\(s\)から出る辺は\((s,2),(s,3)\)の2つがあります。よって\(j\in V,(s,j)\in E\)に当てはまる頂点は2と3の2つです。
従って1つ目の制約式は
\(x_{s2} + x_{s3} = 1\)
となります。変数は0か1しか取らないのでこれは\(x_{s2},x_{s3}\)のどちらが1を取ることを表しています。つまり
「辺\((s,2)\)と辺\((s,3)\)のどちらか1つだけを必ず選ぶ」
ということを表しています。
2つ目の制約
\(\sum\limits_{i \in V,(i,t) \in E}x_{it} = 1\)
2つ目の制約は
「終点に向かう辺を必ず1つだけ選ぶ」
ということを表しています。\(t\)が始点だと思ってください。\(\sum\limits_{i \in V, (i,t) \in E}\)は\(V\)中の頂点\(i\)で\((i,t)\)が\(E\)中の辺であるものを全て足し算するということを表しています。
つまり終点\(t\)に向かう辺に対応する変数を全部足すということを表しています。
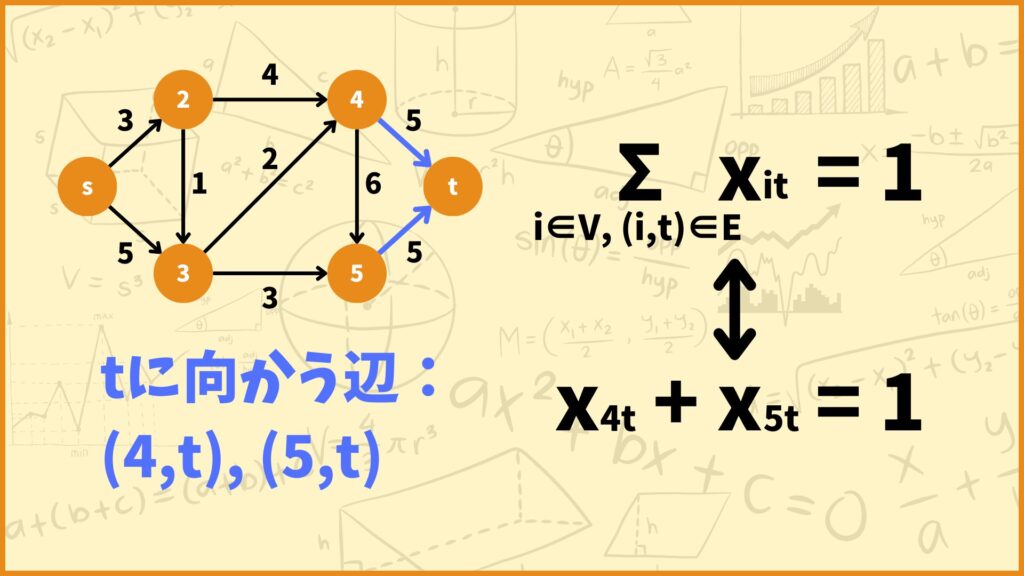
例えば上の例を見てみましょう。終点\(t\)に向かう辺は\((4,t),(5,t)\)の2つがあります。よって\(i\in V,(i,t)\in E\)に当てはまる頂点は4と5の2つです。
従って1つ目の制約式は
\(x_{4t} + x_{5t} = 1\)
となります。変数は0か1しか取らないのでこれは\(x_{4t},x_{5t}\)のどちらが1を取ることを表しています。つまり
「辺\((4,t)\)と辺\((5,t)\)のどちらか1つだけを必ず選ぶ」
ということを表しています。
3つ目の制約
\(\sum\limits_{i \in V,(i,j) \in E}x_{ij}-\sum\limits_{k \in V, (j,k) \in E}x_{jk} = 0 \;\;\; (\forall j \in V/\{s,t\})\)
3つ目の制約は
「ある頂点に向かう辺の数とその頂点から出る辺の数が一致する」
ということを表しています。
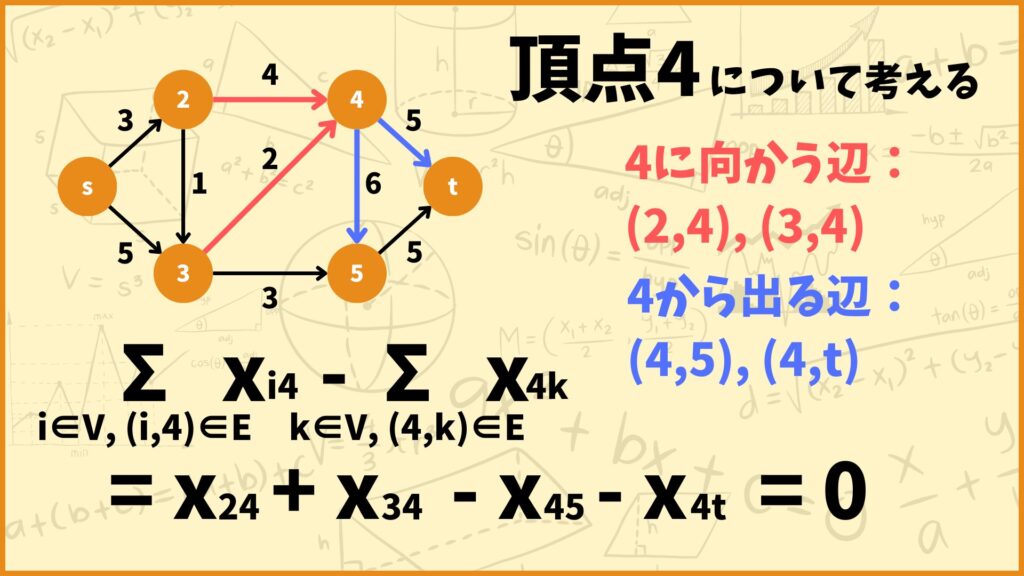
例えば上のグラフの頂点4について考えてみましょう。頂点4に向かう辺は\((2,4),(3,4)\)で頂点4から出る辺は\((4,5),(4,t)\)です。そのため制約式は
\(\sum\limits_{i \in V,(i,4) \in E}x_{i4} – \sum\limits_{k \in V, (4,k) \in E}x_{4k} = x_{24} + x_{34} – x_{45} – x_{4t} = 0\)
となります。例えば\(x_{34} = 1\)、つまり頂点3から頂点4に向かうとします。このとき上の制約式を満たすためには\(x_{45},x_{4t}\)のどちらか一つだけを1にしないといけません。
仮に\(x_{45} = 1\)とします。これはつまり頂点4から頂点5に向かうことを表します。
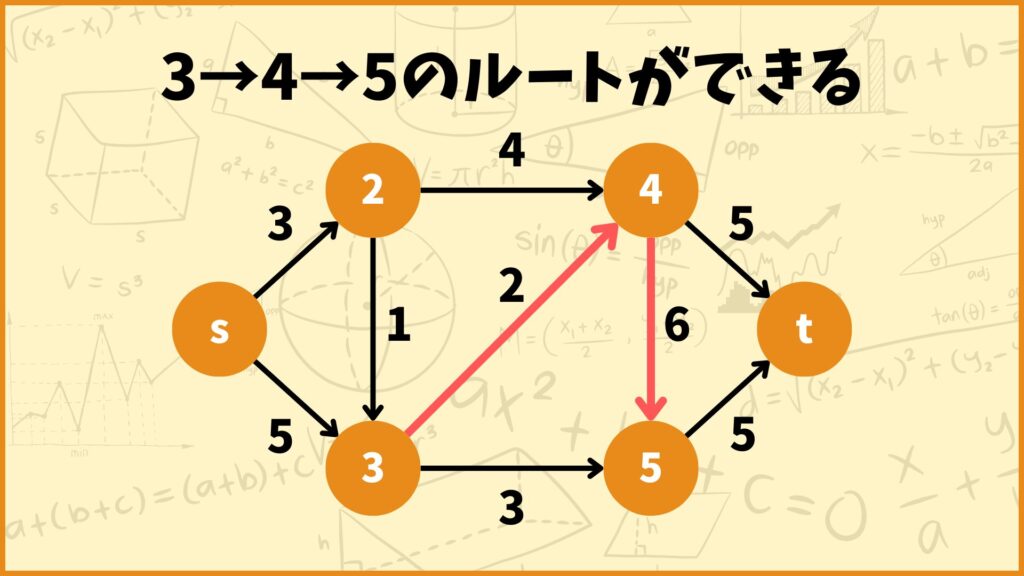
次に頂点4を含まない経路を考えてみます。このとき\(x_{24} = x_{34} = 0\)となるので上の制約式を満たすためには\(x_{45} = x_{4t} = 0\)となる必要があります。
このように3つ目の制約式は「もしその頂点に訪れるならその頂点から他の頂点に移動し、その頂点に訪れないならその頂点から他の頂点には移動しない」というのを表す制約です。
整数計画問題としてまとめる
以上のことを踏まえて整数計画問題として定式化しましょう。
パラメータ:
\(V\) : 頂点集合
\(E\) : 辺集合
\(w_{ij}\) : 辺\((i,j)\)の重み
変数:
\(x_{ij} \in \{0,1\}\) : 辺\((i,j)\)を採用するなら1、そうでないなら0を取る0-1変数
定式化:
\( \min \;\;\; \sum\limits_{(i,j) \in E}w_{ij}x_{ij}\)
\(\;\text{s.t.}\;\;\;\sum\limits_{j \in V,(s,j) \in E}x_{sj} = 1\)
\(\;\;\;\;\;\;\;\;\; \sum\limits_{j \in V,(j,t) \in E}x_{jt} = 1\)
\(\;\;\;\;\;\;\;\;\; \sum\limits_{i \in V,(i,j) \in E}x_{ij}-\sum\limits_{k \in V, (j,k) \in E}x_{jk} = 0 \;\;\; (\forall j \in V/\{s,t\})\)
\(\;\;\;\;\;\;\;\;\; x_{ij} \in \{0,1\} \;\;\; (\forall (i,j) \in E)\)
ということで整数計画問題として定式化することができました。
pythonで解いてみた
それでは実際にこの問題をpythonで解いてみましょう。結論以下のプログラムを実行することで問題を解くことができます。
## 事前準備
from pulp import *
## 記号の設定
V = [1,2,3,4,5,6] # 地点の設定
V_st = [2,3,4,5] # 始点と終点以外の地点の設定
E = [(1,2),(1,3),(2,3),(2,4),(3,4),(3,5),(4,5),(4,6),(5,6)] # 辺の設定
# 辺の重みの設定
w = {(1,2) : 3,
(1,3) : 5,
(2,3) : 1,
(2,4) : 4,
(3,4) : 2,
(3,5) : 3,
(4,5) : 6,
(4,6) : 5,
(5,6) : 5}
## 整数計画問題として定式化したものを解く
# 問題を最小化に設定
prob = pulp.LpProblem(sense = LpMinimize)
# 変数を設定
x = LpVariable.dicts("x", [(i,j) for (i,j) in E], cat="Binary")
# 目的関数を設定
prob += lpSum(w[(i,j)] * x[(i,j)] for (i,j) in E)
# 制約条件を設定
prob += lpSum(x[(1,j)] for j in V if (1,j) in E) == 1
prob += lpSum(x[(i,6)] for i in V if (i,6) in E) == 1
for j in V_st:
prob += lpSum(x[(i,j)] for i in V if (i,j) in E) - lpSum(x[(j,k)] for k in V if (j,k) in E) == 0
# 問題を解く
result = prob.solve()
## 結果の表示
# 解の状態を表示
print(LpStatus[result])
# 最適解の表示(値が1の変数だけ表示)
for (i,j) in E:
if x[i,j].value() == 1:
print(f"x_({i},{j}) =", x[i,j].value())
# 最適値の表示
print("最適値 :",prob.objective.value())
これらのプログラムを実行したら上の結果が得られました。それでは1つずつ説明していきます。
プログラムの説明
事前準備
## 事前準備
from pulp import *
問題を解くための事前準備としてpulpをインポートしましょう。pulpはpythonで数理計画問題を解くのに使います。
記号の設定
## 記号の設定
V = [1,2,3,4,5,6] # 地点の設定
V_st = [2,3,4,5] # 始点と終点以外の地点の設定
E = [(1,2),(1,3),(2,3),(2,4),(3,4),(3,5),(4,5),(4,6),(5,6)] # 辺の設定
# 辺の重みの設定
w = {(1,2) : 3,
(1,3) : 5,
(2,3) : 1,
(2,4) : 4,
(3,4) : 2,
(3,5) : 3,
(4,5) : 6,
(4,6) : 5,
(5,6) : 5}
次に記号の設定の所を説明します。
2行目では地点の集合を設定しています。今回は\(s=1,t = 6\)とします。
3行目では\(V/\{s,t\}\)を設定しています。
4行目で辺の設定をしています。
6~14行目では辺の重みを設定しています。
整数計画問題として定式化したものを解く
## 整数計画問題として定式化したものを解く
# 問題を最小化に設定
prob = pulp.LpProblem(sense = LpMinimize)
# 変数を設定
x = LpVariable.dicts("x", [(i,j) for (i,j) in E], cat="Binary")
# 目的関数を設定
prob += lpSum(w[(i,j)] * x[(i,j)] for (i,j) in E)
# 制約条件を設定
prob += lpSum(x[(1,j)] for j in V if (1,j) in E) == 1
prob += lpSum(x[(i,6)] for i in V if (i,6) in E) == 1
for j in V_st:
prob += lpSum(x[(i,j)] for i in V if (i,j) in E) - lpSum(x[(j,k)] for k in V if (j,k) in E) == 0
# 問題を解く
result = prob.solve()
3行目で問題を最小化に設定しています。
5行目で0-1変数\(x_{ij}\)の定義をしています。添字の\(i,j\)は辺\((i,j)\)を表しているので[(i,j) for (i,j) in E]としています。0-1変数なので cat = “Binary”としています。
7行目で目的関数を設定しています。
9~12行目で制約条件を設定しています。
14行目で問題を解いています。
結果を表示する
## 結果の表示
# 解の状態を表示
print(LpStatus[result])
# 最適解の表示(値が1の変数だけ表示)
for (i,j) in E:
if x[i,j].value() == 1:
print(f"x_({i},{j}) =", x[i,j].value())
# 最適値の表示
print("最適値 :",prob.objective.value())
3行目で解の状態を表示します。Optimalと表示されたら最適解が得られています。
5~7行目で最適解を表示しています。
9行目で最適値を表示しています。
結果の解釈

1行目でOptimalと表示されているので最適解が得られていることが分かります。
2~5行目では最適解を表示しています。これを見ると\(x_{12} = x_{23} = x_{34} = x_{46} = 1\)であることが分かります。つまり 1→2→3→4→6のルートが最短経路だと分かりました。

6行目では最適値を表示しています。これを見ると最短経路の長さが11であることが分かります。
地点数をもっと増やしてみた
最後に地点数をもっと増やして計算してみます。
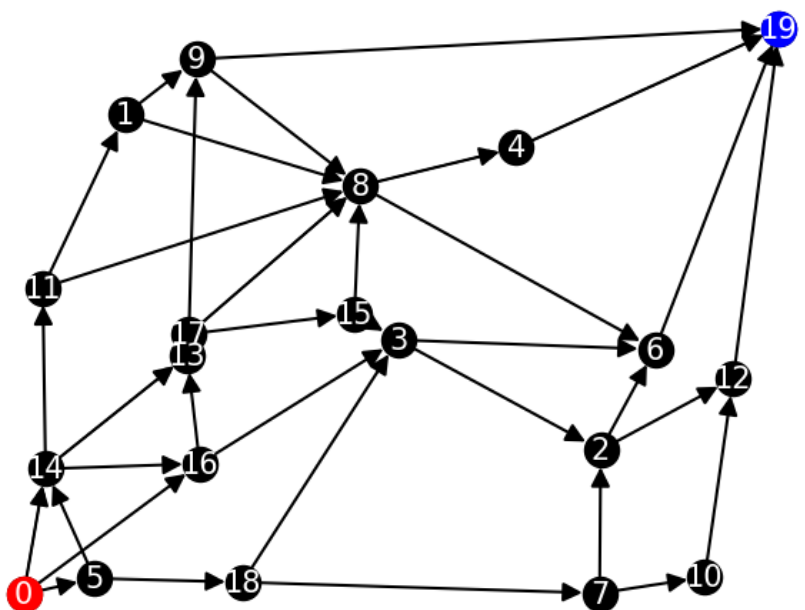
上図のような有向グラフに対して、地点0から地点19までの最短路を求めてみます。
なお各地点は\([0,10] \times[0,10]\)のユークリッド平面上にランダムに配置しており、2地点間の距離はユークリッド距離とします。

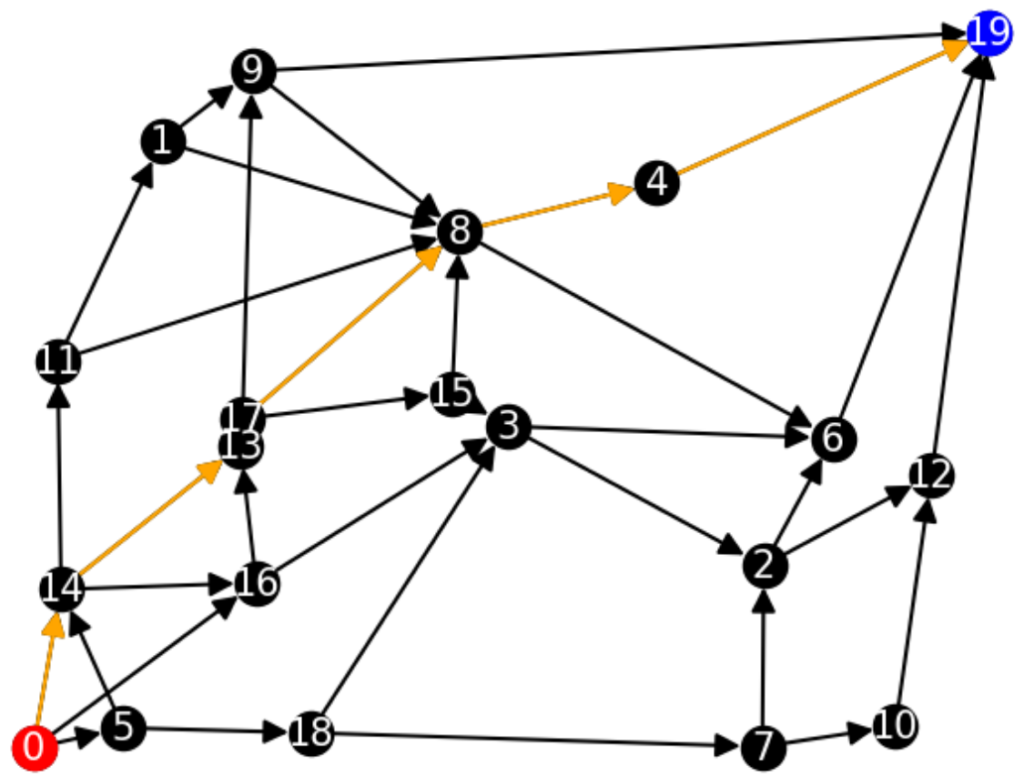
計算結果は上記のようになりました。このことから最短経路は0→14→13→17→8→4→19となります。
おわりに
いかがでしたか。
今回の記事では最短経路問題について解説していきました。
今後もこのような数理最適化に関する記事を書いていきます!
最後までこの記事を読んでくれてありがとうございました。



