こんにちは!しゅんです!
今回の記事は出勤希望を考慮したシフト作成問題を整数計画問題として定式化してpythonで解く方法を解説していきます!
シフト作成問題とは、例えばコンビニのアルバイトのシフトを作成する問題です。どの時間帯に誰がシフトに入るのかを数学を使って決めていきます。
それではやっていきましょう!
普段は組合せ最適化の記事を書いてたりします。
ぜひ他の記事も読んでみてください!
このブログの簡単な紹介はこちらに書いてあります。
興味があったら見てみてください。
このブログでは経営工学を勉強している現役理系大学生が、経営工学に関することを色々話していきます!
ぼくが経営工学を勉強している中で感じたことや、興味深かったことを皆さんと共有出来たら良いなと思っています。
そもそも経営工学とは何なのでしょうか。Wikipediaによると
経営工学(けいえいこうがく、英: engineering management)は、人・材料・装置・情報・エネルギーを総合したシステムの設計・改善・確立に関する活動である。そのシステムから得られる結果を明示し、予測し、評価するために、工学的な分析・設計の原理・方法とともに、数学、物理および社会科学の専門知識と経験を利用する。
引用元 : 経営工学 – Wikipedia
長々と書いてありますが、要は経営、経済の課題を理系的な観点から解決する学問です。
問題設定
24時間営業のコンビニの1週間のシフトを作成することを考える。コンビニでは計10人の従業員がいる。1日の勤務は夜勤(24:00~8:00)、日勤(8:00~16:00)、準夜勤(16:00~24:00)の3種類に分けられる。
シフト作成の際に考慮する条件:
・各従業員は1日のうち最大でも1つの勤務にしか出勤できない。
・各勤務に必要な人数は「日勤:3人、準夜勤:2人、夜勤:1人」である。
・各従業員は全ての曜日の全ての勤務に対して「2:出勤したい、1:どっちでも良い、0:出勤したくない」の評価を付ける。
理想的なシフト:
・従業員が一番満足するようなシフトを作りたい
今回は上記のような問題設定を考えていきます。条件と理想的なシフトについてもう少し丁寧に説明していきます。
各従業員は1日のうち最大でも1つの勤務にしか出勤できない

例えば従業員1が月曜日に日勤をするとします。このとき従業員1は月曜日の夜勤と準夜勤には出勤することができません。
各勤務に必要な人数は「日勤:3人、準夜勤:2人、夜勤:1人」である
これは文字通り各勤務に必要な人数の条件を表しています。
各従業員は全ての曜日の全ての勤務に対して評価を付ける
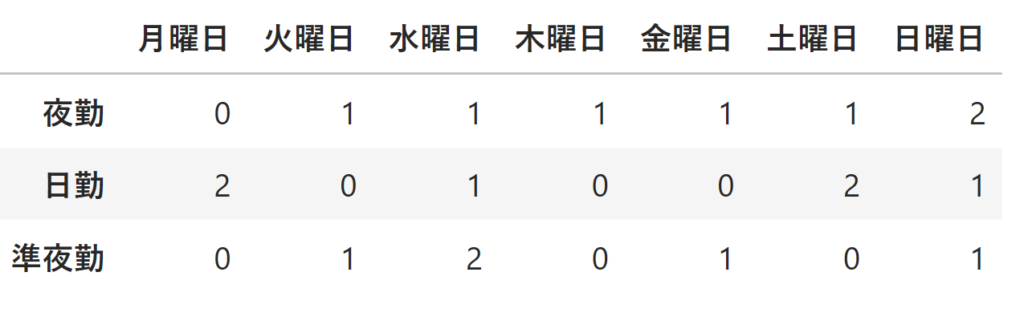
各従業員は全ての勤務に対して上記のような評価を付けます。例えば月曜日の日勤に対する評価は2ですが、これは
「月曜日の日勤に出勤したい」
ということを表しています。他にも例えば木曜日の準夜勤に対する評価は0ですが、これは
「木曜日の準夜勤には出勤したくない」
ということを表しています。
これ以降、評価の数字を評価値と呼びます。
従業員が一番満足するようなシフトを作りたい
上記の評価を考慮して、従業員が一番満足するようなシフトを作成することを目標とします。
例えばさっきの従業員の評価値の表において、その従業員が月曜日の日勤、木曜日の準夜勤、土曜日の日勤に出勤した場合、評価値の合計は\(2+0+2=4\)となります。
直観的に考えると評価値の合計が大きいほど従業員が満足するようなシフトであるとみなせるはずです。
ということで今回は
「全従業員の評価値の合計が最大となるようなシフトを作成する」
ことを目的としたいと思います。
整数計画問題として定式化する
それでは次にシフト作成問題を整数計画問題として定式化する方法を説明します。「記号の定義」、「目的関数の設定」、「制約条件の設定」の3つに分けてそれぞれ説明したいと思います。
記号の定義
パラメータ:
\(P\) : 従業員の集合
\(W\) : 曜日の集合
\(S\) : 勤務の集合
\(n_s\) : 勤務\(s\)に必要な従業員の人数
\(v_{ws}^{p}\) : 従業員\(p\)の曜日\(w\)の勤務\(s\)に対する評価
変数:
\(x_{ws}^{p} \in \{0,1\}\) : 従業員\(p\)が曜日\(w\)の勤務\(s\)に出勤するなら1、そうでないなら0を取る0-1変数
パラメータとして\(P,S,W,n_s,v_{we}^{p}\)を設定します。\(P\)は従業員の集合です。今回の例だと従業員は10人なので
\(P = \{1,2,3,4,5,6,7,8,9,10\}\)
となります。
\(S\)は勤務の集合です。今回の例だと勤務は夜勤、日勤、準夜勤の3種類あるので例えば夜勤を1、日勤を2、準夜勤を3と数字で表すと
\(S = \{1,2,3\}\)
となります。
\(W\)は曜日の集合です。月曜を1、火曜を2、水曜を3、木曜を4、金曜を5、土曜を6、日曜を7とすると
\(W = \{1,2,3,4,5,6,7\}\)
となります。
\(n_s\)は勤務\(s\)に必要な従業員の人数です。今回の例だと
\(n_1=1,n_2=3,n_3=2\)
となります。(夜勤:\(s=1\)、日勤:\(s=2\)、準夜勤:\(s=3\))
\(v_{ws}^{p}\)は従業員\(p\)による曜日\(w\)の勤務\(s\)に対する評価です。

上の表が従業員1による評価値の表だとすると、例えば月曜日\((w=1)\)の日勤\((s=2)\)の評価は2なので
\(v_{12}^{1} = 2\)
となります。
また0-1変数として\(x_{ws}^{p}\)を用います。例えば従業員1が月曜日\((w=1)\)の日勤\((s=2)\)に出勤する場合
\(x_{12}^{1}=1\)
となります。
目的関数の設定
目的関数:
\(\sum\limits_{p \in P}\sum\limits_{w \in W}\sum\limits_{s \in S}v_{ws}^{p}x_{ws}^{p}\)
今回のシフト作成問題の目的は
「評価値の合計が最大となるシフトを作成する」
というものです。

例えば上の評価値を持つ従業員\(p\)が月曜日\((w=1)\)の日勤\((s=2)\)と木曜日\((w=4)\)の夜勤\((s=1)\)に出勤する場合
\(x_{12}^{p} = x_{41}^{p} = 1\)
となり、上記以外の変数の値は0となります。よって\(\sum\limits_{w \in W}\sum\limits_{s \in S}v_{ws}^{p}x_{ws}^{p}\)の値は
\(\sum\limits_{w \in W}\sum\limits_{s \in S}v_{ws}^{p}x_{ws}^{p} = v_{12}^{p}+v_{41}^{p}=2+1=3\)
となり、これは従業員\(p\)が出勤する勤務の評価値の合計と一致していますね。全ての従業員に関してこれを足せば良いので目的関数は
\(\sum\limits_{p \in P}\sum\limits_{w \in W}\sum\limits_{s \in S}v_{ws}^{p}x_{ws}^{p}\)
となります。今回はこの目的関数が最大となる場合を求めたいので問題を\(\text{maximize}\)に設定します。
目的関数を最大化:
\(\max \;\; \sum\limits_{p \in P}\sum\limits_{w \in W}\sum\limits_{s \in S}v_{ws}^{p}x_{ws}^{p}\)
制約条件の設定
制約条件:
\(\sum\limits_{s \in S}x_{ws}^{p} \leq 1 \;\;\; (\forall p \in P, \; \forall w \in W)\)
\(\sum\limits_{p \in P}x_{ws}^{p} = n_s \;\;\; (\forall w \in W, \; \forall s \in S)\)
1つずつ説明していきます。
1つ目の制約条件
1つ目の制約条件:
\(\sum\limits_{s \in S}x_{ws}^{p} \leq 1 \;\;\; (\forall p \in P, \; \forall w \in W)\)
1つ目の制約は
「1日に出勤できる勤務は1つまで」
ということを表しています。例えば従業員1\((p=1)\)の月曜日\((w=1)\)についてこの制約式を考えてみましょう。制約式は以下の通りです。
\(\sum\limits_{s \in S}x_{1s}^{1} = x_{11}^{1}+x_{12}^{1}+x_{13}^{1}\leq 1\)
これは\(x_{11}^{1},x_{12}^{1},x_{13}^{1}\)の中で最大でも1つしか1になれないという式です。
\(x_{11}^{1}\)は従業員1が月曜日の夜勤に出勤するかどうか、\(x_{12}^{1}\)は従業員1が月曜日の日勤に出勤するかどうか、\(x_{13}^{1}\)は従業員1が月曜日の準夜勤に出勤するかどうかをそれぞれ表しています。
つまりこの式は、「従業員1は月曜日の夜勤、日勤、準夜勤のうち、最大でもいずれか1つまでしか出勤できない」ということを表しています。この制約式が全ての従業員の全ての曜日に対して存在するので、「1日に出勤できる勤務は1つまで」という制約式を表しています。
1つ目の制約条件:
\(\sum\limits_{s \in S}x_{ws}^{p} \leq 1 \;\;\; (\forall p \in P, \; \forall w \in W)\)
2つ目の制約条件
2つ目の制約条件:
\(\sum\limits_{p \in P}x_{ws}^{p} = n_s \;\;\; (\forall w \in W, \; \forall s \in S)\)
2つ目の制約条件は
「各勤務に出勤する人数は必要人数と一致する」
ということを表しています。例えば月曜日\((w=1)\)の日勤\((s=2)\)についてこの制約式を考えてみましょう。\(n_2=3\)(日勤に必要な人数は3人)なので制約式は以下のようになります。
\(\sum\limits_{p \in P}x_{12}^{p} =x_{12}^{1}+x_{12}^{2}+x_{12}^{3}+…+x_{12}^{10}=3\)
これは\(x_{12}^{1},x_{12}^{2},x_{12}^{3},…,x_{12}^{10}\)のいずれか3つが1になるということを表しています。
例えば\(x_{12}^{1}=x_{12}^{3}=x_{12}^{8}=1\)になるとしましょう。これは「月曜日の日勤に従業員1,3,8の3人が出勤する」ということを表していて、日勤に必要な従業員数を満たしていますね。
この制約式が全ての曜日の全ての勤務に対して存在するので、「各勤務に出勤する人数は必要人数と一致する」という制約式になっています。
2つ目の制約条件:
\(\sum\limits_{p \in P}x_{ws}^{p} = n_s \;\;\; (\forall w \in W, \; \forall s \in S)\)
整数計画問題としてまとめる
以上のことを踏まえて整数計画問題として定式化しましょう。
パラメータ:
\(P\) : 従業員の集合
\(W\) : 曜日の集合
\(S\) : 勤務の集合
\(n_s\) : 勤務\(s\)に必要な従業員の人数
\(v_{ws}^{p}\) : 従業員\(p\)の曜日\(w\)の勤務\(s\)に対する評価
変数:
\(x_{ws}^{p} \in \{0,1\}\) : 従業員\(p\)が曜日\(w\)の勤務\(s\)に出勤するなら1、そうでないなら0を取る0-1変数
目的関数:
\(\max \;\; \sum\limits_{p \in P}\sum\limits_{w \in W}\sum\limits_{s \in S}v_{ws}^{p}x_{ws}^{p}\)
制約条件:
\(\sum\limits_{s \in S}x_{ws}^{p} \leq 1 \;\;\; (\forall p \in P, \; \forall w \in W)\)
\(\sum\limits_{p \in P}x_{ws}^{p} = n_s \;\;\; (\forall w \in W, \; \forall s \in S)\)
\(x_{ws}^{p} \in \{0,1\} \;\;\; (\forall p \in P, \; \forall w \in W, \; \forall s \in S)\)
ということで整数計画問題として定式化することができました。
pythonで解いてみた
それでは実際にこの問題をpythonで解いてみましょう。結論以下のプログラムを実行することで問題を解くことができます。
## 事前準備
from pulp import * #pulpをインポート
import pandas as pd # pandasをインポート
import random # randomをインポート
random.seed(1) # 毎回同じ乱数が生成されるようにする
## 記号の設定
P = [p for p in range(10)] # 従業員の集合
W = [w for w in range(7)] # 曜日の集合(0:月、1:火、2:水、3:木、4:金、5:土、6:日)
S = [s for s in range(3)] #勤務の集合(0:夜勤、1:日勤、2:準夜勤)
n = [1,3,2] # 各勤務に必要な人数の設定
v = [[[0 for _ in S] for _ in W] for _ in P] # 各従業員の評価リストの初期設定
for p in P:
for w in W:
for s in S:
v[p][w][s] = random.randint(0,2) # 各従業員の各曜日の各勤務に対する評価をランダムに設定
W_NAME = {0:"月",
1:"火",
2:"水",
3:"木",
4:"金",
5:"土",
6:"日",} # 曜日の名前をまとめた辞書(結果の出力用)
S_NAME = {0:"夜勤",
1:"日勤",
2:"準夜勤"} # 勤務の名前をまとめた辞書(結果の出力用)
## 整数計画問題として定式化したものを解く
# 問題を最小化に設定
prob = pulp.LpProblem(sense = LpMaximize)
# 目的関数を設定
x = LpVariable.dicts("x", (P,W,S), cat="Binary")
# 目的関数を設定
prob += lpSum(v[p][w][s]*x[p][w][s] for p in P for w in W for s in S)
# 制約条件を設定
for p in P:
for w in W:
prob += lpSum(x[p][w][s] for s in S) <= 1 # 1日に出勤できる勤務は1つまでとする制約
for w in W:
for s in S:
prob += lpSum(x[p][w][s] for p in P) == n[s] # 各勤務に出勤する人数を必要人数と一致させる制約
# 問題を解く
result = prob.solve()
## 結果の表示
print("解の状態 :",LpStatus[result]) # 解の状態を表示
print("最適値 :",prob.objective.value()) # 最適値の表示
# 最適解の表示(値が1の変数だけ表示)
for p in P:
for s in S:
for w in W:
if x[p][w][s].value() == 1:
print(f"x_従業員{p+1}_"+"_"+W_NAME[w]+"_"+S_NAME[s])
これらのプログラムを実行したら上の結果が得られました。それではコードが何を表しているのか、そして得られた結果の見方について1つずつ解説していきます。
コードの解説
「事前準備」、「記号の設定」、「整数計画問題として定式化して解く」、「結果の表示」の4つに分けてそれぞれ解説していきます。
事前準備
## 事前準備
from pulp import * #pulpをインポート
import pandas as pd # pandasをインポート
import random # randomをインポート
random.seed(1) # 毎回同じ乱数が生成されるようにする
ここではpulp,pandas.randomをインポートし、毎回同じ乱数が生成されるようにしています。
pulpはpythonで整数計画問題を扱うために使います。
pandasは問題を解くこと自体には使いませんが、結果を見やすく表示するために使います。
randomはpythonで乱数を扱うために使います。
random.seed()でプログラムの実行時に毎回同じ乱数が生成されるようにします。(これ書かないと毎回結果が変わってしまいます。)
記号の設定
## 記号の設定
P = [p for p in range(10)] # 従業員の集合
W = [w for w in range(7)] # 曜日の集合(0:月、1:火、2:水、3:木、4:金、5:土、6:日)
S = [s for s in range(3)] #勤務の集合(0:夜勤、1:日勤、2:準夜勤)
n = [1,3,2] # 各勤務に必要な人数の設定
v = [[[0 for _ in S] for _ in W] for _ in P] # 各従業員の評価リストの初期設定
for p in P:
for w in W:
for s in S:
v[p][w][s] = random.randint(0,2) # 各従業員の各曜日の各勤務に対する評価をランダムに設定
W_NAME = {0:"月",
1:"火",
2:"水",
3:"木",
4:"金",
5:"土",
6:"日",} # 曜日の名前をまとめた辞書(結果の出力用)
S_NAME = {0:"夜勤",
1:"日勤",
2:"準夜勤"} # 勤務の名前をまとめた辞書(結果の出力用)
2行目で従業員の集合を設定しています。
3行目で曜日の集合を設定しています。0が月曜、1が火曜、…と言う風に数字で曜日を設定しています。
4行目で勤務の集合を設定しています。0が夜勤、1が日勤、2が準夜勤という風に数字で勤務の種類を設定しています。
5行目で各勤務に必要な人数の設定をしています。0番目が夜勤、1番目が日勤、2が準夜勤の必要人数をそれぞれ表しています。
6~10行目で各従業員の各曜日の各勤務に対する評価を設定しています。6行目で評価リストの初期設定をし、7~10行目で0,1,2のいずれかの数字をランダムに設定しています。random.randint(0,2)は0以上2以下の整数をランダムに生成してくれます。

例えば上記の評価リストは従業員1のものです。
11~17行目で数字と曜日を結びつける辞書を作っています。問題を解くだけなら必要ないですが、計算結果を見やすくするために用います。
18~20行目で数字と勤務を結びつける辞書を作っています。これも問題を解くだけなら必要ないですが、計算結果を見やすくするために用います。
pythonでは数字が0から始まっていることに注意してください。のちに説明しますがこれにより解を表示するときはp+1を表示するようにしています。
整数計画問題として定式化して解く
## 整数計画問題として定式化したものを解く
# 問題を最小化に設定
prob = pulp.LpProblem(sense = LpMaximize)
# 目的関数を設定
x = LpVariable.dicts("x", (P,W,S), cat="Binary")
# 目的関数を設定
prob += lpSum(v[p][w][s]*x[p][w][s] for p in P for w in W for s in S)
# 制約条件を設定
for p in P:
for w in W:
prob += lpSum(x[p][w][s] for s in S) <= 1 # 1日に出勤できる勤務は1つまでとする制約
for w in W:
for s in S:
prob += lpSum(x[p][w][s] for p in P) == n[s] # 各勤務に出勤する人数を必要人数と一致させる制約
# 問題を解く
result = prob.solve()
3行目で問題を最大化に設定しています。「sense = LpMinimize」だと目的関数を最小化する問題に設定できます。
5行目で変数を設定しています。「LpVariable.dicts()」は変数をいっぺんに設定できるので変数が多いときに便利です。括弧の中身は左から順に(”変数名”, 添字の集合, 変数の種類)となっています。
変数\(x_{ws}^{p}\)の添字はそれぞれ\(p\)が集合\(P\)、\(w\)が集合\(W\)、\(s\)が集合\(S\)中の要素なので添字の集合は(P,W,S)とします。
「cat = “Binary”」で変数を0-1変数に設定しています。連続変数にしたければ「cat = “Continuous”」とします。
7行目で目的関数を設定しています。pulpで\(\sum\)は「lpSum」で表現できます。「x[p][w][s]」と設定することで\(x_{ws}^{p}\)、「for p in P for w in W for s in S」と設定することで\(p \in P,w \in W,s \in S\)を表現できます。
9~14行目で制約条件を設定しています。9~11行目で1つ目の制約条件、12~14行目で2つ目の制約条件をそれぞれ設定しています。
16行目で問題を解いています。問題を解くときは「.solve()」でできます。
結果の表示
## 結果の表示
print("解の状態 :",LpStatus[result]) # 解の状態を表示
print("最適値 :",prob.objective.value()) # 最適値の表示
# 最適解の表示(値が1の変数だけ表示)
for p in P:
for s in S:
for w in W:
if x[p][w][s].value() == 1:
print(f"x_従業員{p+1}_"+"_"+W_NAME[w]+"_"+S_NAME[s])
2行目で解の状態を表示しています。Optimalと表示されたら最適解が得られています。
3行目で最適値を表示しています。
5~9行目で最適解を表示しています。値が1の変数だけ表示するようにしています。「f”x_従業員{p+1}_”」としているのはリストPが0から始まるからです。数字がずれても特に問題はないですが、これまでの説明と合わせるために「p」ではなく「p+1」としています。
結果の解釈

上記のプログラムを実行したら上のような結果が得られました。1つずつ見ていきます。
1行目は解の状態を表しています。Optimalと表示されているので最適解が得られています。
2行目は最適値を表しています。今回のシフト作成問題の最適値は76であることが分かりました。
3行目以降は最適解を表しています。例えば従業員1は水曜の夜勤、月曜の日勤、土曜の日勤で勤務するようです。
もう少し詳しく結果を見てみましょう。
金曜日と土曜日のシフトを見てみる
全部見るのは大変なので代表して金曜日と土曜日のシフトを見てみましょう。
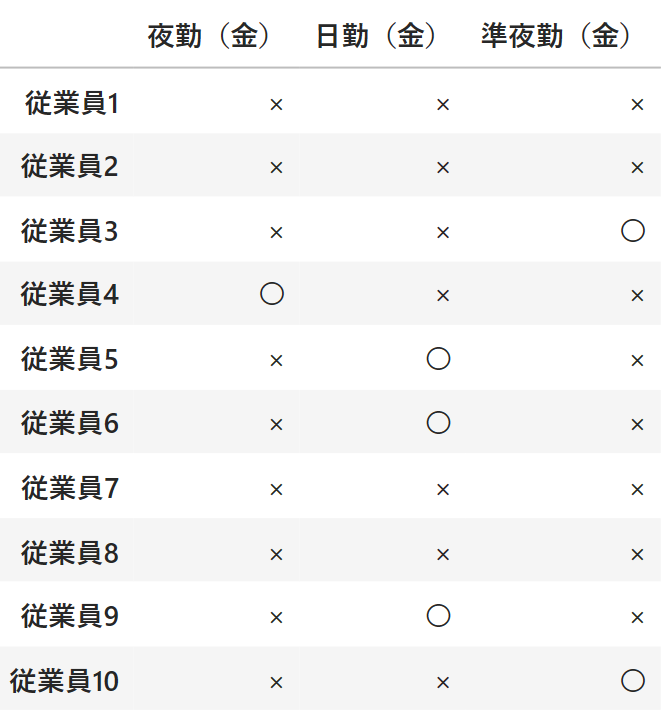

上記の左の表が金曜のシフト、右の表が土曜のシフトをそれぞれ表しています。〇が付いている人が出勤することを表しています。
これを見るとちゃんと夜勤は1人、日勤は3人、準夜勤は2人になっていて、どの従業員も1日最大1勤務までになっていますね。
上の表を表示するコードは以下の通りです。本題ではないので説明は省略します。
## 金曜日のシフトを表示するコード
LIST_FRI = [[0 for _ in S] for _ in P]
for p in P:
for s in S:
if x[p][4][s].value() == 1:
LIST_FRI[p][s] = "〇"
else:
LIST_FRI[p][s] = "×"
df_FRI = pd.DataFrame(LIST_FRI, columns = [S_NAME[s]+"(金)" for s in S], index= [f"従業員{i+1}" for i in P])
df_FRI## 土曜日のシフトを表示するコード
LIST_SAT = [[0 for _ in S] for _ in P]
for p in P:
for s in S:
if x[p][5][s].value() == 1:
LIST_SAT[p][s] = "〇"
else:
LIST_SAT[p][s] = "×"
df_SAT = pd.DataFrame(LIST_SAT, columns = [S_NAME[s]+"(土)" for s in S], index= [f"従業員{i+1}" for i in P])
df_SAT各従業員が希望の勤務に出勤できているかを見てみる
次に従業員が希望の勤務に出勤できているかを確かめてみましょう。
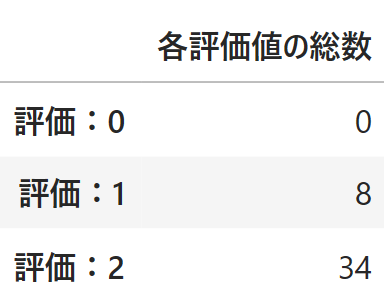
上の表の1行目から順に、全従業員がそのように評価した勤務に出勤した回数を表しています。つまり全42回の勤務の中で、34回は評価2、つまり「出勤したい」と評価した勤務に出勤しており、8回は評価1、つまり「どっちでも良い」と評価した勤務に出勤しているということです。
これを見ると評価0、つまり「出勤したくない」と評価した勤務に出勤する人が1人もいないということが分かります。ということでちゃんと出勤希望を考慮できていることが分かりますね。
上記の表を表示するコードは以下の通りです。本題ではないので説明は省略します。
COUNT_1 = [0,0,0]
for p in P:
for w in W:
for s in S:
if x[p][w][s].value() == 1:
COUNT_1[v[p][w][s]] += 1
df_COUNT_1 = pd.DataFrame(COUNT_1, index = [f"評価:{i}" for i in [0,1,2]], columns = ["各評価値の総数"])
df_COUNT_1各従業員の出勤回数を見てみる
最後に各従業員の出勤回数を見てみましょう。
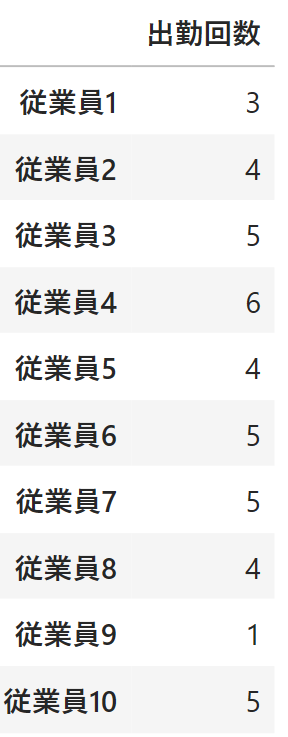
上の表は各従業員の出勤回数を表しています。例えば従業員1は3回出勤していますね。最も出勤しているのは6回出勤している従業員4で、最も出勤していないのは1回しか出勤していない従業員9であることが分かります。
上記の表を表示するコードは以下の通りです。本題ではないので説明は省略します。
COUNT_2 = [0 for _ in P]
for p in P:
for w in W:
for s in S:
if x[p][w][s].value() == 1:
COUNT_2[p] += 1
df_COUNT_2 = pd.DataFrame(COUNT_2, index = [f"従業員{i+1}" for i in P], columns = ["出勤回数"])
df_COUNT_2数理モデルの問題点とその改善策
ここまでは出勤希望を考慮したシフト作成問題を整数計画問題として定式化してpythonで解く方法を紹介してきました。ところがこの数理モデルによって得られたシフトにはいくつか問題点があるように思えます。
ということで最後に今回定式化した整数計画問題の問題点の中から2点選び、その改善策について考えてみたいと思います。
従業員の出勤回数に偏りがある
1つ目の問題点は従業員の出勤回数に偏りがあるという点です。

先ほどの出勤回数の表を見ると分かるように、従業員4は1回しか出勤していないにもかかわらず従業員6は6回も出勤していることが分かります。このようなシフトだと従業員から不公平だという声が上がるかもしれません。
この問題の改善策として「出勤回数の下限を設ける」というものが挙げられます。例えば最低でも週に2回は出勤するといった制約を追加することによって出勤回数の偏りを抑えることができます。
「最低でも週に2回は出勤する」という制約式は以下のように表すことができます。
\(\sum\limits_{w \in W}\sum\limits_{s \in S}x_{ws}^{p} \geq 2 \;\;\; (\forall p \in P)\)
問題点その1:
出勤回数に偏りがある
改善策の例:
出勤回数の下限を設ける
準夜勤→次の日の夜勤に出勤する人が出てしまう

2つ目の問題点はある日の準夜勤とその次の日の夜勤両方に出勤する人がでてしまうという点です。これの何が問題かと言うと、準夜勤→日勤を連続で働くことになるので16時間連続で働くことになってしまいます。


今回作成したシフトでも、従業員3が「金曜の準夜勤→土曜の夜勤」に割り当てられています。このようなシフトは使えないので修正する必要がありそうです。
この問題の改善策として、「準夜勤→次の日の夜勤を禁止する」というものが挙げられます。
「準夜勤→次の日の夜勤を禁止する」という制約式は以下のように表すことができます。
\(x_{w_{mod7}3}^{p}+x_{(w+1)_{mod7}1}^{p} \leq 1 \;\;\; (\forall p \in P, \; \forall w \in W)\)
なお\(w_{mod7}\)は\(w\)を7で割った時の余りを表しています。これは日曜→月曜の話をするときに\(mod7\)を付けないとうまくいかないためです。
問題点その2:
準夜勤→次の日の夜勤に割り当てられる
改善策の例:
準夜勤→次の日の夜勤を禁止する
おわりに
いかがでしたか。
今回の記事ではシフト作成問題について解説していきました。
今後もこのような組合せ最適化に関する記事を書いていきます!
最後までこの記事を読んでくれてありがとうございました。




