【これでわかる！】pythonを使ってパーセプトロンを実装する方法をなるべくわかりやすく解説してみた

こんにちは！しゅんです！

今回はパーセプトロンをpythonで実装する方法について解説していきます！

それではやっていきましょう！

入力が2個の場合

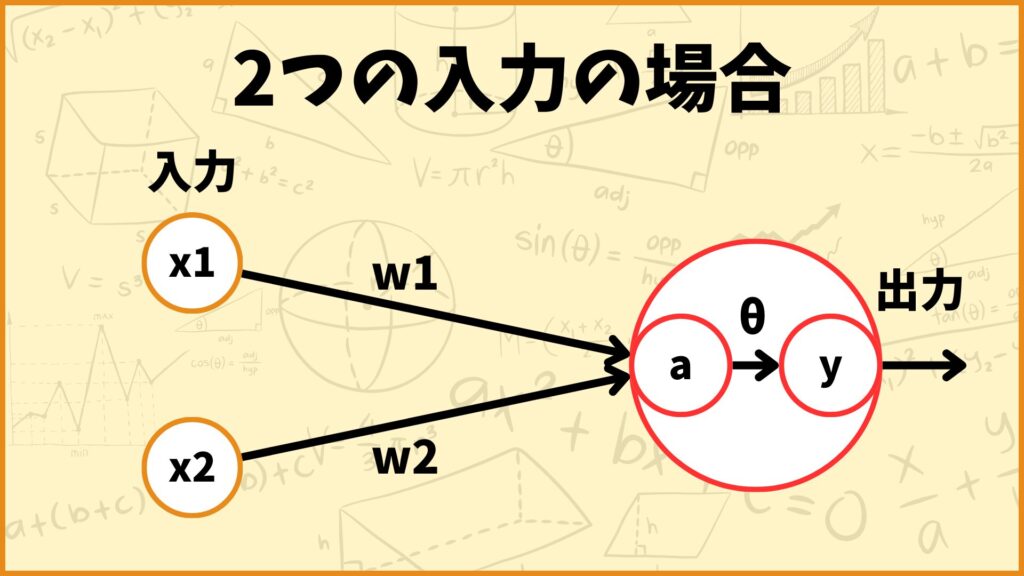
上図は2個の入力の場合のパーセプトロンを表しています。この図を使ってパーセプトロンで何が起こっているのかを解説します。

今\(x_1,x_2\)を入力します。このとき入力された値は重み付けされて足し算されます。（重み付けされて足し算されたものを重み付き和と言ったりします。）

例えば\(x_1\)の重みを\(w_1\)、\(x_2\)の重みを\(w_2\)、重み付き和を\(a\)とすると

\(a = w_1x_1 + w_2x_2\)

となります。例えば\((x_1,x_2) = (1,2), \; (w_1,w_2) = (2,3)\)のとき重み付き和\(a\)は

\(a = 2 \times 1+3 \times 2 = 8\)

と計算できます。

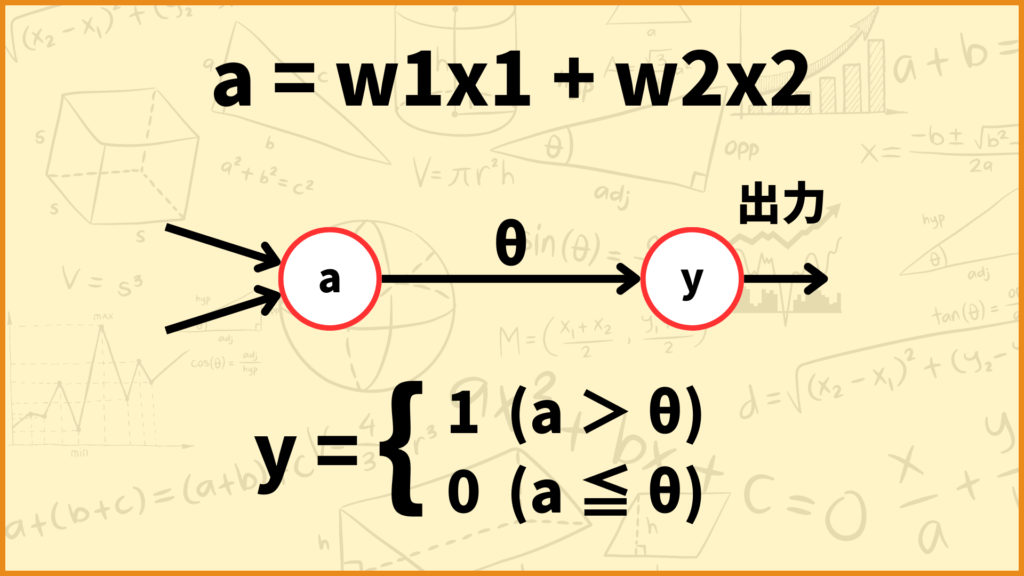
重み付き和\(a\)が計算出来たら次にこの\(a\)と\(\theta\)を比べます。\(a > \theta\)だったら\(y=1\)とし、\(a \leq \theta\)だったら\(y = 0\)とします。

例えば\(a = 8, \; \theta = 6\)のとき\(a > \theta\)なので\(y = 1\)となります。

これがパーセプトロンの中で起こっている一連の流れです。

入力が3個の場合

今までは入力が2個の場合を説明しましたが、入力が3個の場合でも同じように計算することができます。

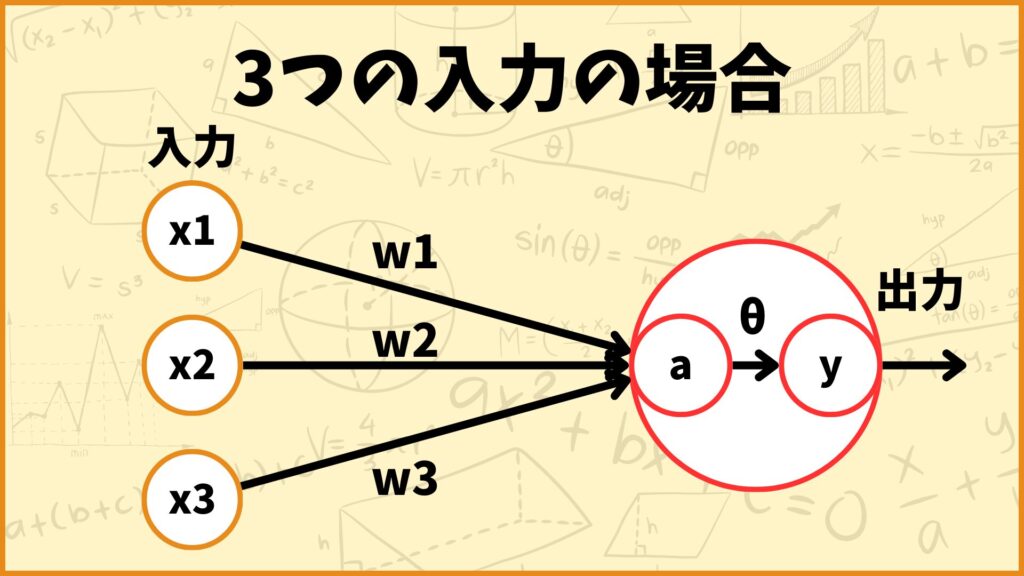
今\(x_1,x_2,x_3\)の3つの値が入力されたとします。このとき\(a\)は

\(a = w_1x_1+w_2x_2+w_3x_3\)

と計算でき、\(a>\theta\)なら\(y=1\)、\(a\leq\theta\)なら\(y=0\)となります。

入力がn個の場合

一般に入力が\(n\)個の場合でも同じように計算することができます。

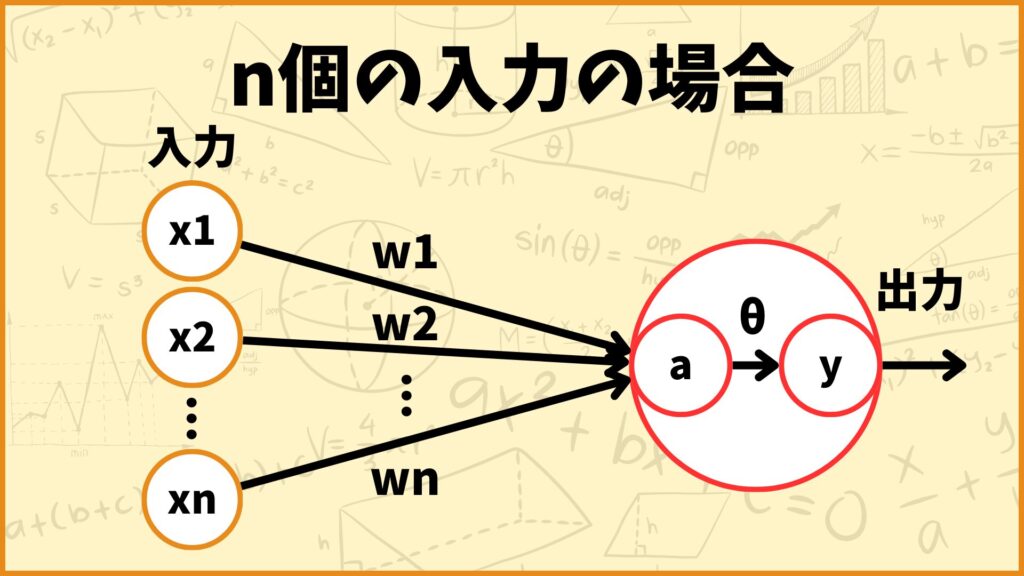
今\(x_1,x_2,…,x_n\)が入力されたとします。このとき\(a\)は

\(a = w_1x_1+w_2x_2+…+w_nx_n=\sum\limits_{i = 1}^n w_ix_i\)

と計算でき、\(a>\theta\)なら\(y=1\)、\(a\leq\theta\)なら\(y=0\)となります。

今回の記事では3パターンのコードの書き方でパーセプトロンをpythonで実装していきたいと思います。なお3パターンは全て関数として定義しています。

1つ目の書き方

1つ目のコードの説明

# 入力が2個の場合のパーセプトロン
def perceptron1(x,w,b):
    weighted_sum = w[0]*x[0] + w[1]*x[1] + b
    if weighted_sum > 0:
        return 1
    else:
        return 0  # パーセプトロンの関数定義はここまで

#入力例
x = [1, 2]
w = [2, 3]
b = -5
print(perceptron1(x,w,b))

1つ目のコードではリスト中の要素を1つずつ指定する方法でパーセプトロンを実装しました。

2行目で関数の定義をしています。関数の名前はperceptron1、引数は「x」、「w」、「b」です。なお「x」は入力値、「w」は重み、「b」はバイアスを表し、「x」、「w」の型はリストを想定していてます。

3行目で重み付き和を計算しています。重み付き和は\(w_1x_1+w_2x_2+b\)なのでこれを「weighted_sum」としています。（重み付き和は英語で weighted sumと言ったりします。）

4～5行目では重み付き和「weighted_sum」が0より大きかったら1を返すようにしています。

6～7行目では重み付き和「weighted_sum」が0以下だったら0を返すようにしています。

パーセプトロンの関数定義はここまでで、これより下のコードは実際にこの関数に数値を入力した結果を見るコードになっています。例えば

\((x_1,x_2) = (1,2)\)
\((w_1,w_2) = (2,3)\)
\(b = -5\)

を入力したときは以下の結果が得られます。

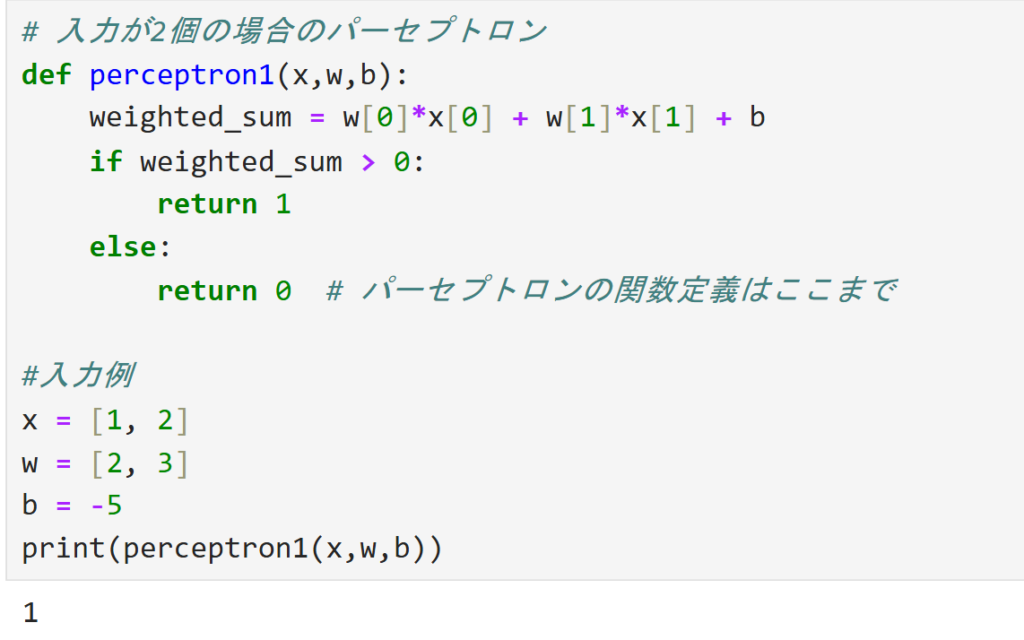
上の画像はこのコードを実行した結果です。これを見ると1が返されています。重み付き和の値は

\(w_1x_1+w_2x_2+b = 1\times2 + 2\times3-5 = 3 > 0\)

となるので1が返されます。ということでちゃんと機能していますね。念のため「weighted_sum」の値も確認してみましょう。

# 入力が2個の場合のパーセプトロン
def perceptron1(x,w,b):
    weighted_sum = w[0]*x[0] + w[1]*x[1] + b
    print(f"weighted_sumの値：{weighted_sum}")
    if weighted_sum > 0:
        return 1
    else:
        return 0  # パーセプトロンの関数定義はここまで

#入力例
x = [1, 2]
w = [2, 3]
b = -5
print(perceptron1(x,w,b))

さっきのコードに「print(f”weighted_sumの値：{weighted_sum}”)」を追加しただけです。このコードを実行すると上の結果が得られ、ちゃんと「weighted_sum」の値が3になっていることが分かります。

2つ目、3つ目のコードには初めから
「print(f”weighted_sumの値：{weighted_sum}”)」
を付けています。

1つ目のコードの問題点

1つ目のコードの問題点は、入力が2個の場合にしか使えないということです。例えば入力が3個の場合は以下のようにコードを書き替える必要があります。

# 入力が3個の場合のパーセプトロン
def perceptron1(x,w,b):
    weighted_sum = w[0]*x[0] + w[1]*x[1] + w[2]*x[2] + b  # ここを書き換える！
    print(f"weighted_sumの値：{weighted_sum}")
    if weighted_sum > 0:
        return 1
    else:
        return 0  # パーセプトロンの関数定義はここまで

#入力例
x = [1, 2, 3]
w = [2, 3, 4]
b = -21
print(perceptron1(x,w,b))

上のコードは入力が3個の場合のパーセプトロンを実装したコードですが、「weighted_sum」の計算式をさっきと変えています。

さっきのままだと\(w_3x_3\)を重み付き和に加えることができないので「weighted_sum = w[0]x[0] + w[1]x[1] + w[2]*x[2] + b」と書き換える必要があります。

このように「x,」、「w」の長さが変わるごとに毎回コードを変えるのは面倒くさいです。

2つ目の書き方

2つ目のコードの説明

# 入力が何個でも良いパーセプトロン
def perceptron2(x,w,b):
    weighted_sum = b  # weighted_sumの初期値を設定
    for i in range(len(x)):  # リストxの長さ分だけfor文を回す
        weighted_sum += w[i]*x[i]  # w_i*x_iを足す
    print(f"weighted_sumの値：{weighted_sum}")
    if weighted_sum > 0:
        return 1
    else:
        return 0  # パーセプトロンの関数定義はここまで

#入力例
x = [1, 2]
w = [2, 3]
b = -5
print(perceptron2(x,w,b))

2つ目のコードではfor文を使って重み付き和を計算する方法でパーセプトロンを実装しました。

3～5行目以外は1つ目のコード同じなので3～5行目以外の説明は省略し、3～5行目について詳しく見ていきます。（関数名はperceptron2にしています。）

3行目では「weighted_sum」の初期値を「b」に設定しています。

4～5行目で「weighted_sum」を計算しています。詳しく見ていきましょう。

4行目ではfor文によってリスト「x」の長さ分だけ回しています。例えばxの長さが3だったら「i = 0, 1, 2」について考えています。

5行目では各iに対して「weighted_sum」に「w[i] * x[i]」を足し算していきます。

このコードはfor文でリスト「x」の長さを取得しているため、入力の長さが2個でも3個でも100個でも使うことができます。

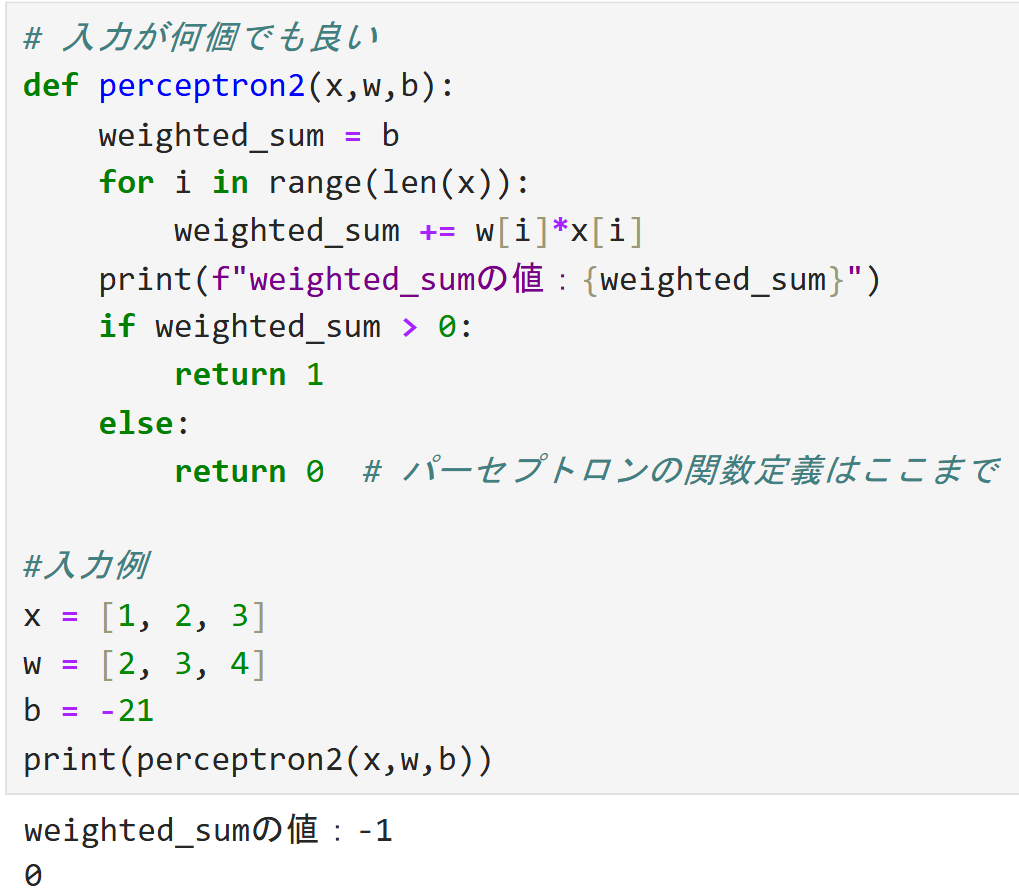
上図のような感じで入力例を色々いじっても、コードを変えることなくちゃんと動くことが分かります。

2つ目のコードの問題点

2つ目のコードの問題点は、計算時間がかかってしまうということです。なぜなら重み付き和を計算する過程でfor文を使っているからです。この部分に時間がすごくかかってしまいます。

3つ目の書き方

3つ目のコードの説明

# numpyを使って実装する
import numpy as np
def perceptron3(x,w,b):
    weighted_sum = np.dot(w,x) + b
    print(f"weighted_sumの値：{weighted_sum}")
    if weighted_sum > 0:
        return 1
    else:
        return 0  # パーセプトロンの関数定義はここまで


#入力例
x = np.array([1, 2, 3])
w = np.array([2, 3, 4])
b = -21
print(perceptron3(x,w,b))

3つ目のコードではnumpyを使って重み付き和を計算する方法でパーセプトロンを実装しました。numpyはpythonで数値計算を効率的に行うためのライブラリです。 機械学習やAIを実装するときに非常によく使われるライブラリです。

2行目でnumpyをインポートしています。このコードによってnumpyを使えるようになります。

4行目以外は1つ目、2つ目のコード同じなので4行目以外の説明は省略し、4行目について詳しく見ていきます。

4行目ではnumpyの「np.dot」という機能を使って「weighted_sum」を計算しています。「np.dot」はベクトルの内積や行列の積を計算することができる機能です。

「np.dot」は「w」と「x」の長さが一緒であればどんな長さでも計算できるので、入力の長さが2個でも3個でも100個でも使うことができます。

入力例の所で「np.array()」を使っています。「np.array()」を使うことによってデータがnumpy.ndarray型になります。

numpy.ndarray型の説明は本題ではないので省略します。ここではnumpyで使えるリストというイメージを持ってもらえばOKです。なお、numpy.ndarrayはリストと同じで「x[1]」といった感じで要素を指定することができます。そのためperceptron2関数にnumpy.ndarray型の入力をしてもちゃんと動きます。

「np.dot()」は「w」と「x」の長さが一緒であればどんな長さを入力しても計算できます。従って入力数が2個でも3個でも100個でも使うことができます。

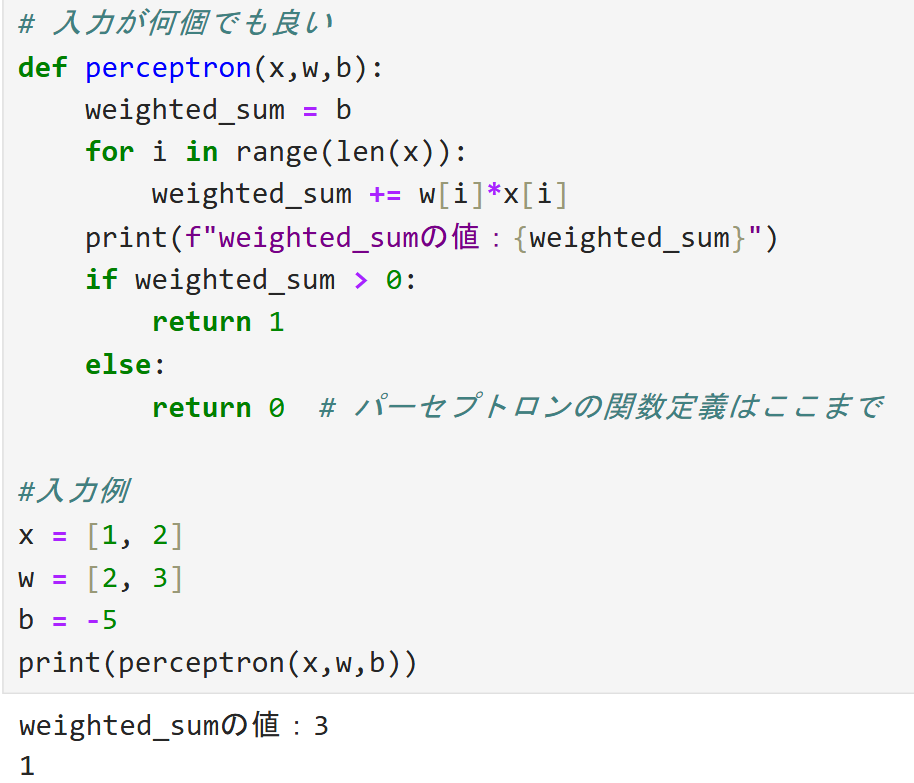
上図のような感じで入力例を色々いじってもコードを変えることなくちゃんと動くことが分かります。

それではこれまで定義してきたパーセプトロンに色々な数値を代入したときにどうなるかをグラフを使って確認してみましょう。2次元グラフにするために\(x,w\)は2次元とします。

例1）\((w_1,w_2)=(1,2), \; b = -5\)

import numpy as np
import matplotlib.pyplot as plt

# パーセプトロンの関数定義
def perceptron3(x, w, b):
    weighted_sum = np.dot(w, x) + b
    if weighted_sum > 0:
        return 1
    else:
        return 0 

# 重みとバイアスの定義
w = np.array([1, 2])
b = -5

# グラフ描画の準備
plt.figure(figsize=(6, 6))  # グラフのサイズを指定

# 整数格子点を作成
x1_range = np.arange(0, 6) 
x2_range = np.arange(0, 6)
X1, X2 = np.meshgrid(x1_range, x2_range)

# 各格子点でパーセプトロンの出力を計算
Z = np.array([[perceptron3(np.array([x1, x2]), w, b) for x1 in x1_range] for x2 in x2_range])

# パーセプトロンの出力に基づいて色分けしてプロット
plt.scatter(X1[Z==1], X2[Z==1], color="r", marker="o", label="1")
plt.scatter(X1[Z==0], X2[Z==0], color="b", marker="x", label="0")

# 境界線をプロット
x1_decision = np.linspace(0, 5, 2)  # 決定境界のためのx1の値
x2_decision = (-w[0] * x1_decision - b) / w[1]  # 決定境界の式
plt.plot(x1_decision, x2_decision, color="g", linestyle="--", label="Boundary")

plt.xlabel("x1")
plt.ylabel("x2")
plt.title("Perceptron Output")
plt.legend()
plt.grid(True)
plt.show()

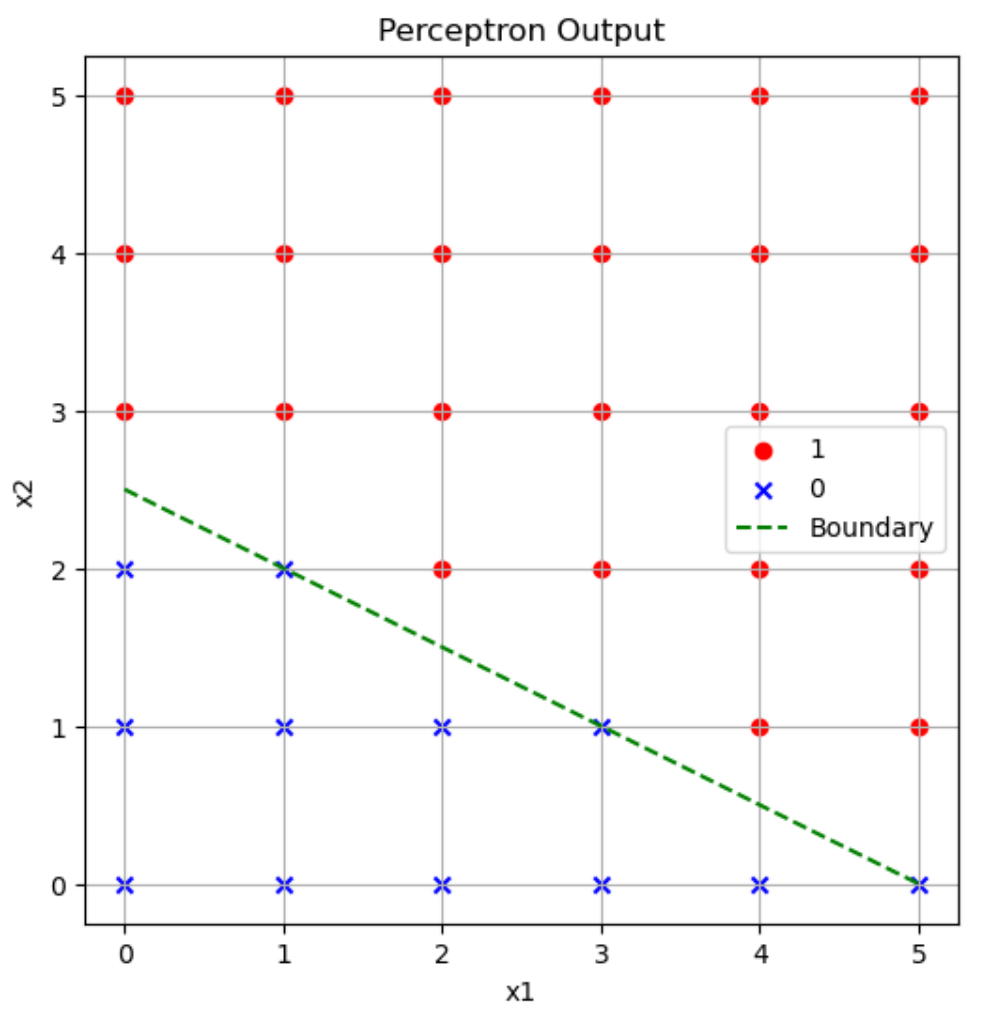
\((w_1,w_2) = (1,2), b = -5\)のとき\(x\)に色々な値を入力した結果が上のグラフのようになります。パーセプトロンが1を返す入力は赤〇、0を返す入力は青×としてプロットしています。

例えば\((x_1,x_2) = (3,4)\)のとき重み付き和は

\(w_1x_1+w_2x_2+b = 1\times3 + 2\times4-5 = 6 > 0\)

なのでパーセプトロンは1を返します。なので\((x_1,x_2) = (3,4)\)の点は赤〇になっています。こんな感じで0以上5以下の整数の組に対して点をプロットした結果が上のグラフです。


緑色の点線はパーセプトロンが1を返すのと0を返す丁度境界を表しています。この点線よりも上側にある点を入力すればパーセプトロンは1を返し、この点線よりも下側にある点を入力すればパーセプトロンは0を返します。

またこの緑色の点線は重み付き和がちょうど0になるラインを表しています。この「重み付き和が0になる」ということを数式で表すと

\(w_1x_1+w_2x_2 + b = 0 \to x_1 + 2x_2 = 5\)

となりこれは緑色の点線、すなわち重みとバイアスがそれぞれ\((w_1,w_2) = (1,2), \; b = -5\)のときのパーセプトロンの境界を表す直線の方程式を表しています。

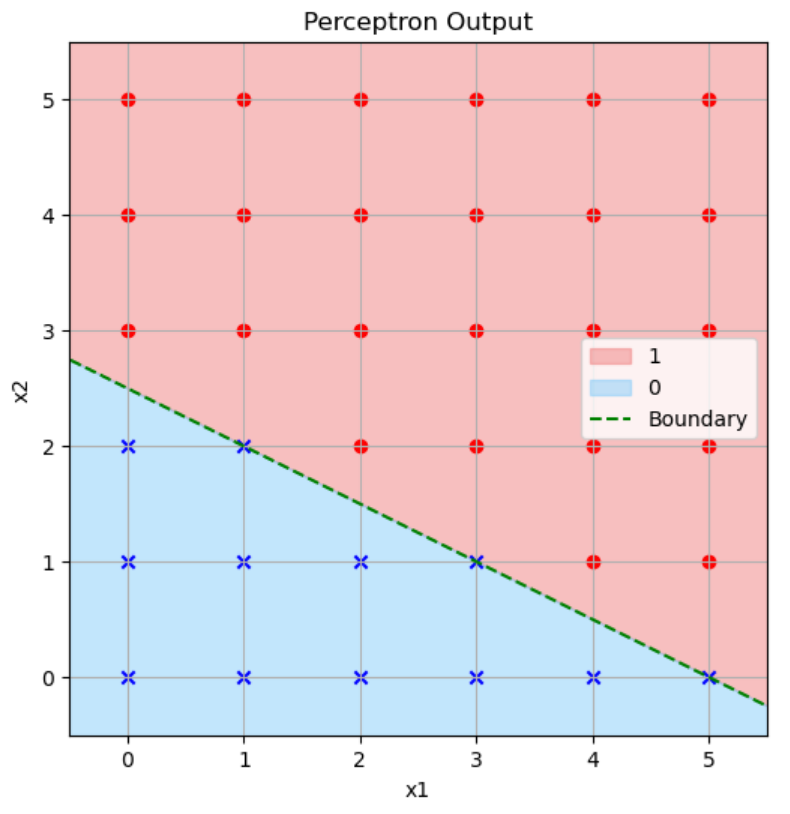
上図は整数の組しかプロットしていませんが、別にパーセプトロンに入力する数字は整数でなくてもOKです。そのように考えると\((w_1,w_2) = (1,2), b = -5\)のときのパーセプトロンに色々な\(x\)を入力すると以下のようなグラフで表せます。

import numpy as np
import matplotlib.pyplot as plt

# パーセプトロンの関数定義
def perceptron3(x, w, b):
    weighted_sum = np.dot(w, x) + b
    if weighted_sum > 0:
        return 1
    else:
        return 0

# 重みとバイアスの定義
w = np.array([1, 2])
b = -5

# グラフ描画の準備
plt.figure(figsize=(6, 6))

# 整数格子点を作成
x1_range = np.arange(0, 6)
x2_range = np.arange(0, 6)
X1, X2 = np.meshgrid(x1_range, x2_range)

# 各格子点でパーセプトロンの出力を計算
Z = np.array([[perceptron3(np.array([x1, x2]), w, b) for x1 in x1_range] for x2 in x2_range])

# 決定境界の直線をプロット
x1_decision = np.linspace(-1, 6, 2)  # 決定境界の x1 の範囲を少し広げる
x2_decision = (-w[0] * x1_decision - b) / w[1]

# 決定境界より上側と下側を塗りつぶし
plt.fill_between(x1_decision, x2_decision, 6, color="lightcoral", alpha=0.5, label="1")  # 上限をグラフの最大値に設定
plt.fill_between(x1_decision, -1, x2_decision, color="lightskyblue", alpha=0.5, label="0")  # 下限をグラフの最小値に設定

# パーセプトロンの出力に基づいて色分けしてプロット (塗りつぶしあり)
plt.scatter(X1[Z==1], X2[Z==1], color="r", marker="o")
plt.scatter(X1[Z==0], X2[Z==0], color="b", marker="x")

plt.plot(x1_decision, x2_decision, color="g", linestyle="--", label="Boundary")

plt.xlabel("x1")
plt.ylabel("x2")
plt.title("Perceptron Output")
plt.xlim(-0.5, 5.5)  # x 軸の範囲を明示的に設定
plt.ylim(-0.5, 5.5)  # y 軸の範囲を明示的に設定
plt.legend()
plt.grid(True)
plt.show()

上図の赤色の領域はパーセプトロンが1を返す領域で、青色の領域はパーセプトロンが0を返す領域で、緑色の点線がその境界をそれぞれ表しています。

例2）\((w_1,w_2)=(10,-7), \; b = 15\)

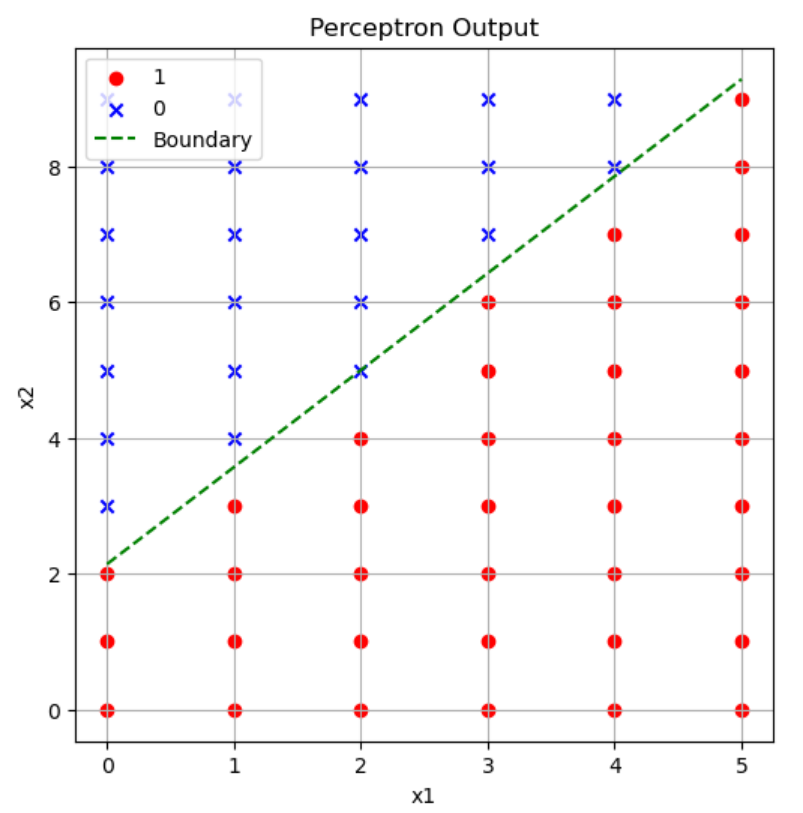
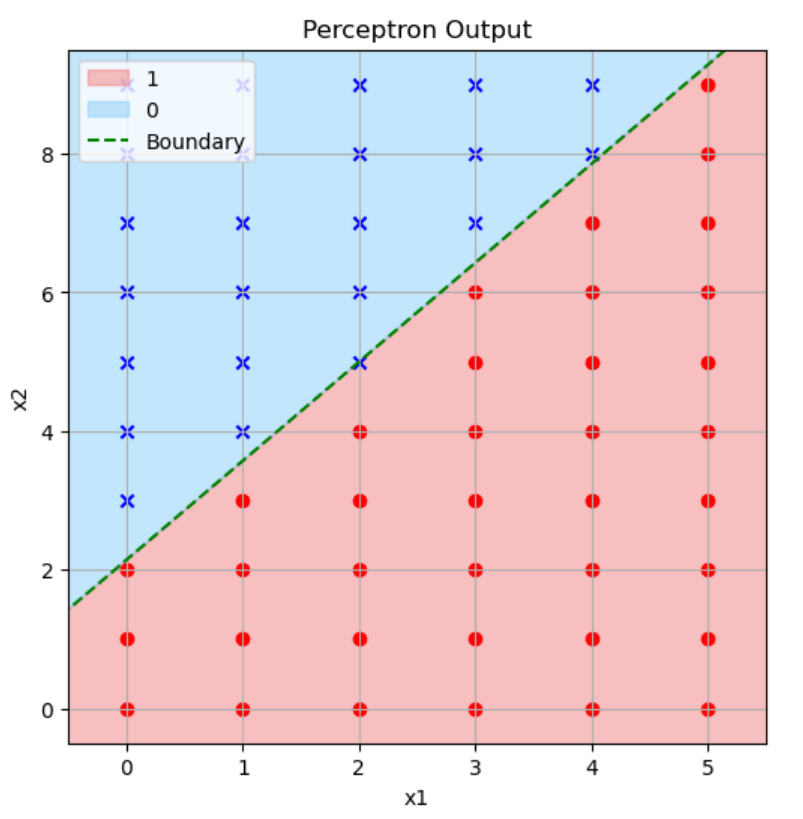
グラフの見方は例1と同じなので詳細な説明は省きます。例えば\((x_1,x_2) = (3,5)\)のとき重み付き和の値は

\(w_1x_1+w_2x_2+b = 10\times3-7\times5+15 = 10 > 0\)

となるのでパーセプトロンは1を返します。（上図だと赤〇になっています。）

他にも例えば\((x_1,x_2) = (1,4)\)のとき重み付き和の値は

\(w_1x_1+w_2x_2+b = 10\times1-7\times4+15 = -3 \leq 0\)

となるのでパーセプトロンは0を返します。（上図だと青×になっています。）

最後におまけとして第3章で紹介した2つ目のコードと3つ目のコードの計算時間を比較してみます。

## 事前準備
import time
import random
import numpy as np
import matplotlib.pyplot as plt
random.seed(1)


## 2つのパーセプトロンの関数を定義
# リストを使って定義
def perceptron2(x,w,b):
    weighted_sum = b
    for i in range(len(x)):
        weighted_sum += w[i]*x[i]
    if weighted_sum > 0:
        return 1
    else:
        return 0
# numpyを使って定義
def perceptron3(x,w,b):
    weighted_sum = np.dot(w,x) + b
    if weighted_sum > 0:
        return 1
    else:
        return 0


## 計算時間を計測
elapsed_time_list2 = []  # perceptron2の計算時間を格納するリスト
elapsed_time_list3 = []  # perceptron3の計算時間を格納するリスト
n_list = [10**i for i in range(1, 8)]  # 入力の個数を表すリスト（「10, 100, 1000, 10000, 100000, 1000000, 10000000」）
for n in n_list:
    x = np.array([random.randint(0,10) for _ in range(n)])  # 入力xを設定
    w = np.array([random.randint(0,10) for _ in range(n)])  # 重みwを設定
    b = -25*n  # バイアスbを設定
    
    # perceptron2の計算時間を計測
    start_time2 = time.time()
    perceptron2(x,w,b)
    end_time2 = time.time()
    elapsed_time_list2.append(end_time2 - start_time2)
    
    # perceptron3の計算時間を計測
    start_time3 = time.time()
    perceptron3(x,w,b)
    end_time3 = time.time()
    elapsed_time_list3.append(end_time3 - start_time3)


## グラフの作成
# FigureとAxesの設定
fig, ax = plt.subplots(figsize=(10, 6))

# データのプロット
ax.plot(n_list, elapsed_time_list2, marker="s", linestyle="-", color="darkslateblue", label="perceptron2", alpha = 0.7, lw = 2)
ax.plot(n_list, elapsed_time_list3, marker="o", linestyle="-", color="lightseagreen", label="perceptron3", alpha = 0.7, lw = 2)

# 対数スケールの設定
ax.set_xscale("log")

# ラベルの設定
ax.set_xlabel("Input Size (log scale)", fontsize=12)
ax.set_ylabel("Elapsed Time (seconds)", fontsize=12)
ax.set_title("Comparison of Elapsed Time for perceptron2 and perceptron3", fontsize=14)

# グリッド線の表示
ax.grid(True, linestyle="--", alpha=0.7)

# 凡例の表示
ax.legend(fontsize=12)

# 図の表示
plt.show()

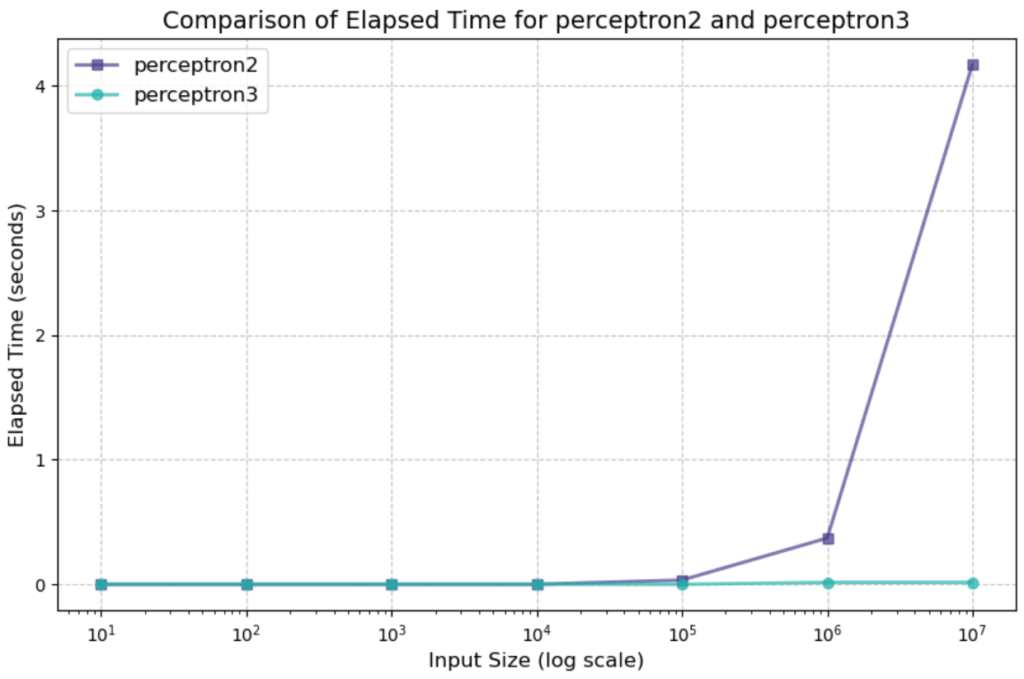
上のグラフは入力数を\(10^1～10^7\)まで大きくしたときの計算時間を比較しています。紫のグラフが2つ目のコード、緑のグラフが3つ目のコードの計算時間をそれぞれ表しています。

これを見ると入力数が\(10^5\)くらいまでは2つ目のコードも3つ目のコードもほぼ0秒で計算することができています。

一方で入力数が\(10^6,10^7\)まで大きくなるとだんだんと差が広がっています。3つ目のコードだと入力数\(10^7\)でもほぼ0秒で計算が終わっていますが、2つ目のコードだと入力数\(10^7\)で4秒以上かかっていますね。

いかがでしたか。

今回の記事ではパーセプトロンを解説しました。

今後もこのようなAI・機械学習に関する記事を書いていきます！

最後までこの記事を読んでくれてありがとうございました。

参考文献

ゼロから作るDeep Learning Pythonで学ぶディープラーニングの理論と実装 [ 斎藤 康毅 ]

created by Rinker

¥3,740 (2025/01/03 11:36:22時点 楽天市場調べ-詳細)

book:18172266

• 楽天市場