こんにちは!しゅんです!
今回は自己相関について解説していきたいと思います。
自己相関は周期的な変化があるデータを分析するときに使います。ぼくが最近統計検定の勉強をしていたときにでてきたので皆さんにもシェアしたいと思います!また今回は説明と一緒にpythonを使ってどんなものか確かめたいと思います。
それでは解説していきましょう!
普段はNBAのデータ分析をしたりしています。ぜひこちらの記事も読んでみてください!
このブログでは経営工学を勉強している現役理系大学生が、経営工学に関することを色々話していきます!
ぼくが経営工学を勉強している中で感じたことや、興味深かったことを皆さんと共有出来たら良いなと思っています。
そもそも経営工学とは何なのでしょうか。Wikipediaによると
経営工学(けいえいこうがく、英: engineering management)は、人・材料・装置・情報・エネルギーを総合したシステムの設計・改善・確立に関する活動である。そのシステムから得られる結果を明示し、予測し、評価するために、工学的な分析・設計の原理・方法とともに、数学、物理および社会科学の専門知識と経験を利用する。
引用元 : 経営工学 – Wikipedia
長々と書いてありますが、要は経営、経済の課題を理系的な観点から解決する学問です。
説明に使うデータ
自己相関の説明をするために、まずはアイスの月別の売上データを見てみましょう。
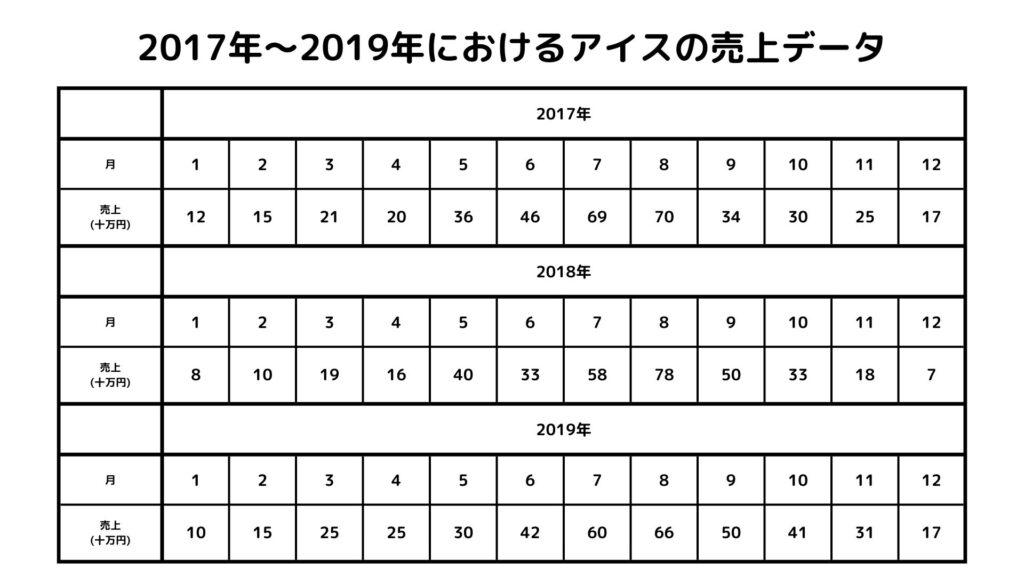
上のデータは2017年から2019年の3年間における、ある店の月別アイス売上データです。折れ線グラフで見ると下のようになります。
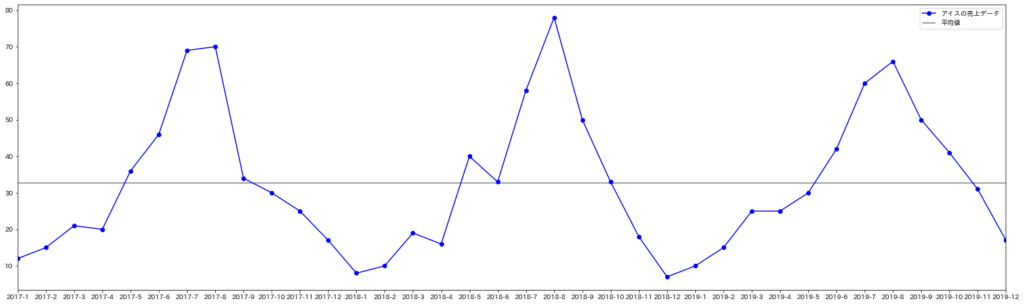
このグラフを見ると1年周期で規則性がありそうですね。アイスが夏に最も売れて冬に最も売れないのは直観的にも想像できますね。
このデータを使って自己相関を説明していきます。
自己相関ってなに?
自己相関はあるデータとそこから一定期間をずらしたデータとの相関のことを言います。例えば2017年1月~2018年12月の24か月間のデータと2018年1月~2019年12月の24か月間のデータとの相関などです。
データをどれだけずらしたかをラグと呼び、この例だとラグは12カ月です。
自分のデータ同士の相関を求めるから自己相関と呼ぶわけですね。
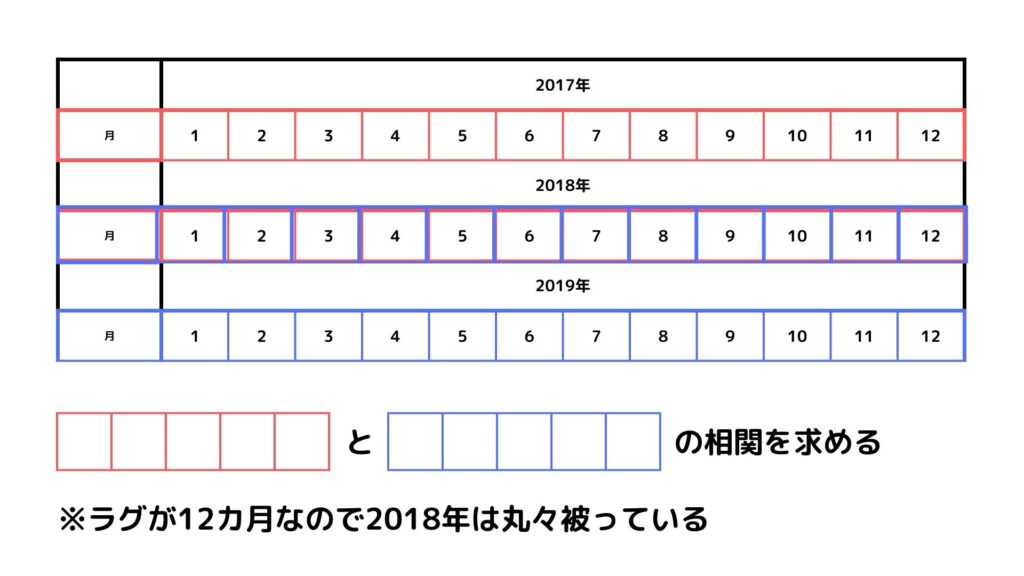
アイスの売り上げは12カ月周期で変化しているので、例えばラグが12の倍数のときは自己相関係数が高そうです。逆にラグが6,18,30のときは自己相関係数が低そうですね。
それでは実際にpythonを使って計算してみましょう。
自己相関をpythonで計算してみる
自己相関係数はpandasのautocorrを使って計算することができます。
# pandasをpdとしてインポート
import pandas as pdまずはデータを作成しましょう。
# アイスの売上データを作成
data = pd.Series([12,15,21,20,36,46,69,70,34,30,25,17,8,10,19,16,40,33,58,78,50,33,18,7,10,15,25,25,30,42,60,66,50,41,31,17],
index =["2017-1","2017-2","2017-3","2017-4","2017-5","2017-6","2017-7","2017-8","2017-9","2017-10","2017-11","2017-12","2018-1","2018-2","2018-3","2018-4","2018-5","2018-6","2018-7","2018-8","2018-9","2018-10","2018-11","2018-12","2019-1","2019-2","2019-3","2019-4","2019-5","2019-6","2019-7","2019-8","2019-9","2019-10","2019-11","2019-12"])ラグが6,12,18,24の場合の計算をしてみましょう。
# ラグが6,12,18,24のときの自己相関係数を表示する
for i in [6,12,18,24]:
print(data.autocorr(lag=i))
ということで計算できました。上から順にラグが6,12,18,24のときの自己相関係数を表しています。
やはり先ほどの予想の通りラグが12,24のとに自己相関係数が大きく、6,18のときに自己相関係数が小さいことが分かりますね。
コレログラムってなに?
コレログラムは自己相関係数をグラフで表したものです。横軸がラグ、縦軸が自己相関係数の値になります。
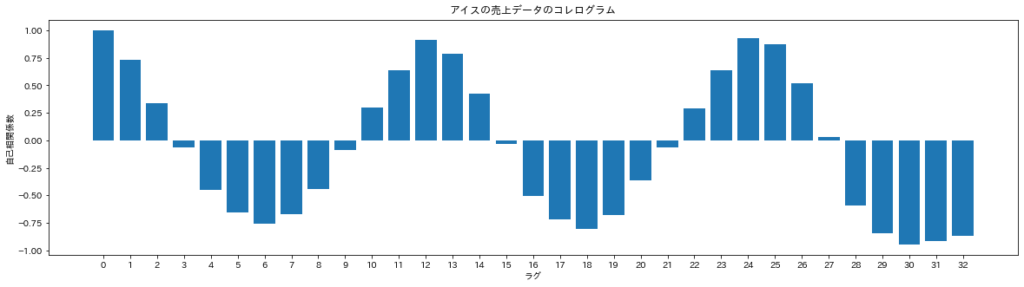
このような感じになります。y=cosxみたいなグラフになっていますね。このように元のデータが周期的だとコレログラムも周期的なものになるようです。
ラグが0,12,24のときに自己相関係数が大きくなり、ラグが6,18,30のときに小さくなっていることが分かります。またラグが3,9,15,21,27のときは自己相関係数がほぼ0ですね。
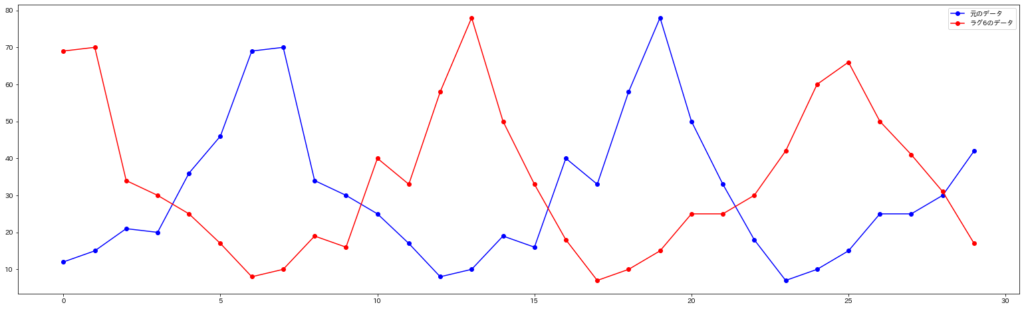
これは元のデータとラグを6にしたときのデータをグラフにしたものです。青が元のデータで赤が6だけずらしたグラフです。これを見ると確かにデータの動きが逆方向になっていることが分かります。
コレログラムをpythonで描いてみる
グラフを描くのでmatplotlibを使いましょう
# matplotlibの日本語版をインポートする
import matplotlib.pyplot as plt
!pip install japanize-matplotlib
import japanize_matplotlib #日本語化matplotlibコレログラムは自己相関係数とそのときのラグをまとめたものなので、先ほどと同じようにautocorrを使います。
# コレログラムの作成
data_auto = [data.autocorr(lag=i) for i in range(33)]
fig = plt.figure(figsize=(20, 5))
ax = fig.add_subplot(111)
ax.bar(list(range(33)),data_auto)
ax.set_xticks(list(range(33)))
ax.set_xlabel("ラグ")
ax.set_ylabel("自己相関係数")
ax.set_title("アイスの売上データのコレログラム")
plt.show()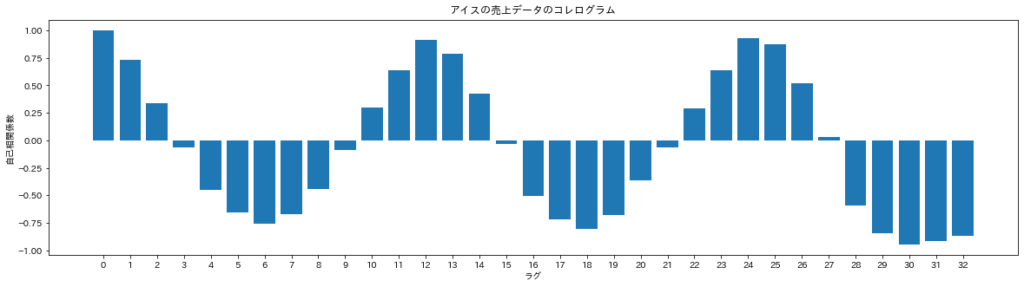
ということでコレログラムを描くことができました。
おわりに
いかがでしたでしょうか。
今回の記事ではpythonで自己相関とコレログラムについて説明していきました。こんな感じでプログラミングを使えばいろいろなことができます。非常に興味深いですよね。
これからもこのようにプログラミングで色々やっていきたいと思います。ぼくが一番勉強になるので続けていきたいです!
最後までこの記事を読んでくれてありがとうございました。
この記事が役に立ったら幸いです。



