こんにちは!しゅんです!
いきなりですが皆さんはローレンツ曲線とジニ係数を知っていますか?
ローレンツ曲線とジニ係数は経済格差を測るときによく使うもので、経済学で使います。ぼくが最近統計検定の勉強をしていたときにでてきたので皆さんにもシェアしたいと思います!今回は説明と一緒にpythonを使ってどんなものか確かめたいと思います。
それでは解説していきましょう!
普段はNBAのデータ分析をしたりしています。ぜひこちらの記事も読んでみてください!
このブログでは経営工学を勉強している現役理系大学生が、経営工学に関することを色々話していきます!
ぼくが経営工学を勉強している中で感じたことや、興味深かったことを皆さんと共有出来たら良いなと思っています。
そもそも経営工学とは何なのでしょうか。Wikipediaによると
経営工学(けいえいこうがく、英: engineering management)は、人・材料・装置・情報・エネルギーを総合したシステムの設計・改善・確立に関する活動である。そのシステムから得られる結果を明示し、予測し、評価するために、工学的な分析・設計の原理・方法とともに、数学、物理および社会科学の専門知識と経験を利用する。
引用元 : 経営工学 – Wikipedia
長々と書いてありますが、要は経営、経済の課題を理系的な観点から解決する学問です。
ローレンツ曲線ってなに?
ローレンツ曲線は経済格差を測るときによく出てくる曲線です。
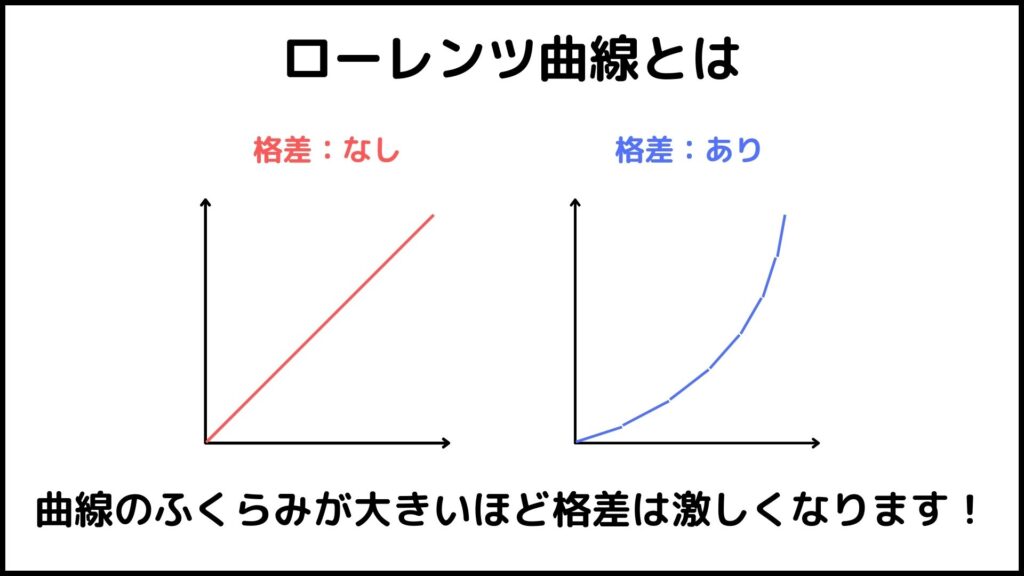
ローレンツ曲線は上の図のようにそのふくらみによって格差がどれくらいあるかを表します。
直線に近づくほど格差は存在せず、曲線がふくらむほど格差が激しくなります。また完全に直線になった場合のローレンツ曲線は完全平等線と一致します。
横軸と縦軸は知りたいデータの累積相対度数を用いてローレンツ曲線を描きます。累積相対度数についてより詳しく知りたい人はこちらの記事もチェックしてみてください!
ローレンツ曲線をpythonで描いてみる
それでは実際にpythonを使ってローレンツ曲線を描いて格差がどれくらいあるのか調べてみましょう。格差を調べる際に用いるデータは以下の3つです。

X社には格差はないですがY社とZ社には格差があるように見えます。とくにZ社の方が格差がありそうですね。(現実でZ社のような会社はないと思いますが、ローレンツ曲線の違いが分かりやすいのでこのデータを使います笑)
今回はローレンツ曲線を描くに当たってnumpyとmatplotlibを使います。これらはデータ分析で欠かせないツールでめちゃめちゃ使います。
# numpy,matplotlibをインポートする
import numpy as np
%matplotlib inline
import matplotlib.pyplot as plt
!pip install japanize-matplotlib
import japanize_matplotlib #日本語化matplotlib3つの会社における従業員の給料データをデータフレーム形式で作成します。
# X社,Y社,Z社のデータを作成
data_X = np.array([0,20,20,20,20,20])
data_Y = np.array([0,10,20,40,60,70])
data_Z = np.array([0,0,0,50,80,120])ローレンツ曲線を描くときに使う給料の累積相対度数を求めます。
# 給料データの相対度数を求める
rel_freq_X = data_X / np.sum(data_X)
rel_freq_Y = data_Y / np.sum(data_Y)
rel_freq_Z = data_Z / np.sum(data_Z)
# 給料データの累積相対度数を求める
rel_cum_freq_X = rel_freq_X.cumsum()
rel_cum_freq_Y = rel_freq_Y.cumsum()
rel_cum_freq_Z = rel_freq_Z.cumsum()給料データの累積相対度数をもとにして3つの会社のローレンツ曲線を描いてみます。なお、給料データの累積相対度数はy軸になります。x軸は従業員の累積相対度数です。今回従業員は5人なので累積相対度数は0.2ずつ増えます。
#ローレンツ曲線を描く
# 従業員の累積相対度数のarrayを作成
rel_cum_freq_emp = np.array([0,0.2,0.4,0.6,0.8,1.0])
fig = plt.figure(figsize = (6,6))
ax = fig.add_subplot(1,1,1)
Lor_curve_X = ax.plot(rel_cum_freq_emp, rel_cum_freq_X, marker = "o", color = "red", label = "会社X")
Lor_curve_Y = ax.plot(rel_cum_freq_emp, rel_cum_freq_Y, marker = "o", color = "blue", label = "会社Y")
Lor_curve_Z = ax.plot(rel_cum_freq_emp, rel_cum_freq_Z, marker = "o", color = "green", label = "会社Z")
ax.set_title("3つの会社のローレンツ曲線")
ax.set_xlabel("従業員数の累積相対度数")
ax.set_ylabel("給料の累積相対度数")
plt.legend()
plt.show()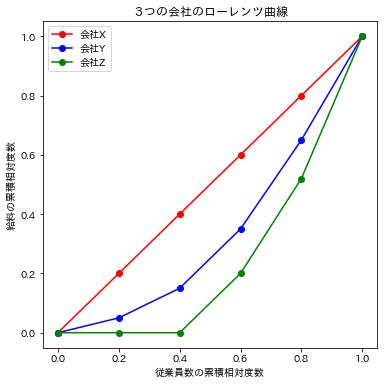
ということで3つの会社におけるローレンツ曲線を描くことができました。やはりX社は完全平等線になりY社、Z社になるにつれてローレンツ曲線のふくらみが大きくなっていますね。
ジニ係数ってなに?
ジニ係数は経済格差を測る指数でローレンツ曲線から求めることができます。

上の図のようにジニ係数は完全平等線とローレンツ曲線で囲まれた面積の2倍で求めることができます。
ジニ係数は0から1で表され1に近づくほど格差が激しくなります。それでは実際に3つの会社における従業員の給料データからそれぞれのジニ係数を求めてみます。
ジニ係数をpythonで求めてみる
折れ線グラフの面積を求めるにあたって今回はscipyを使いたいと思います。scipyは数値解析ソフトウェア・ライブラリで非常に様々なことができます。今回は積分を使って面積を求めますが、積分もscipyでできちゃいます。
それではscipyから積分機能をインストールしていきましょう。
# scipyから積分機能をインストールする
from scipy import integratenp.arrayから積分の計算をするにはintegrate.trapzを使えばできます。
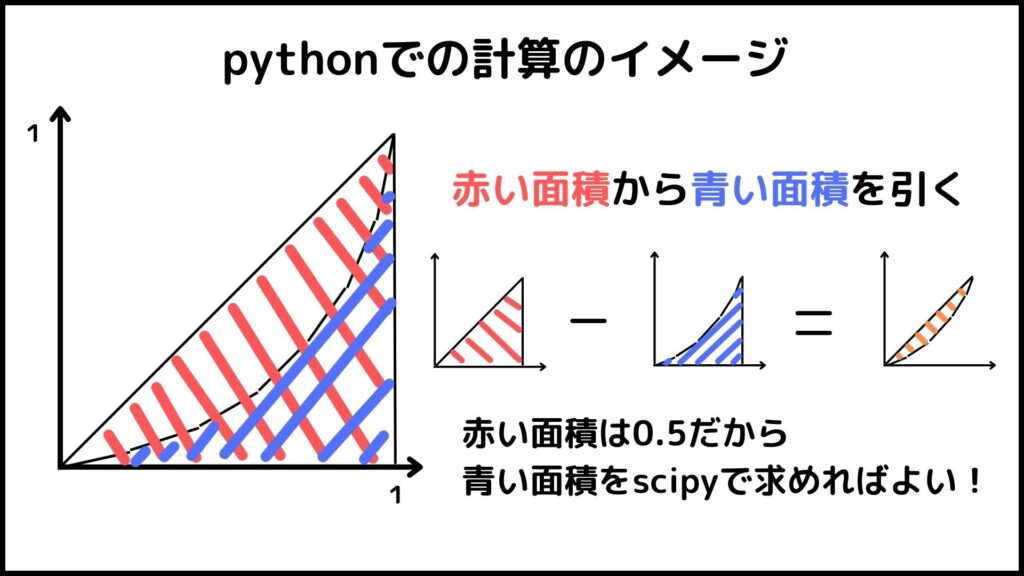
折れ線グラフの座標(xi,yi)をまとめた配列x = [x1,x2,…,xn]とy = [y1,y2,…,yn]があるときx軸と折れ線グラフで囲まれた面積はintegrate.trapz(y,x)で求められます。少し難しいですがやっているのは上図のような計算です。
# scipyから積分機能をインストールする
from scipy import integrate
# ジニ係数を求める
print("会社X :", 2 * (0.5 -integrate.trapz(rel_cum_freq_X, rel_cum_freq_emp)))
print("会社Y :", 2 * (0.5 -integrate.trapz(rel_cum_freq_Y, rel_cum_freq_emp)))
print("会社Z :", 2 * (0.5 -integrate.trapz(rel_cum_freq_Z, rel_cum_freq_emp)))
ということでジニ係数を求めることができました。やはりZ社のジニ係数が一番大きくなっていますね。
ちなみに会社は役職や勤続年数によって給料が違うのでジニ係数の値が大きいからその会社はダメだとかは言えないですね。ある意味当たり前ですが笑
おわりに
いかがでしたでしょうか。
今回の記事ではpythonを使ってローレンツ曲線とジニ係数について説明していきました。こんな感じでプログラミングを使えばいろいろなことができます。非常に興味深いですよね。
これからもこのようにプログラミングで色々やっていきたいと思います。ぼくが一番勉強になるので続けていきたいです!
最後までこの記事を読んでくれてありがとうございました。
この記事が役に立ったら幸いです。




