こんにちは!しゅんです!
今回の記事はなぜベルマンフォード法が(頂点数-1)回の反復で最短距離が求まるのかについて解説していきます!
ベルマンフォード法(Bellman–Ford Algorithm)は重み付き有向グラフにおいて最短経路を求める方法の1つで、負閉路がないグラフであれば最短経路を求めることができます。
ベルマンフォード法のアルゴリズム自体はこちらの記事で解説しています!
負閉路がある場合はこちらの記事で解説しています!
それではやっていきましょう!
普段は統計検定2級の記事を書いてたりします。
ぜひ他の記事も読んでみてください!
このブログの簡単な紹介はこちらに書いてあります。
興味があったら見てみてください。
このブログでは経営工学を勉強している現役理系大学生が、経営工学に関することを色々話していきます!
ぼくが経営工学を勉強している中で感じたことや、興味深かったことを皆さんと共有出来たら良いなと思っています。
そもそも経営工学とは何なのでしょうか。Wikipediaによると
経営工学(けいえいこうがく、英: engineering management)は、人・材料・装置・情報・エネルギーを総合したシステムの設計・改善・確立に関する活動である。そのシステムから得られる結果を明示し、予測し、評価するために、工学的な分析・設計の原理・方法とともに、数学、物理および社会科学の専門知識と経験を利用する。
引用元 : 経営工学 – Wikipedia
長々と書いてありますが、要は経営、経済の課題を理系的な観点から解決する学問です。
ベルマンフォード法のアルゴリズム
STEP.1 最短距離の初期値を始点は0、それ以外の頂点は∞に設定する。
STEP.2 始点から各頂点に対して高々1本の辺を使って到達できる最短経路を探す。
最短距離を更新する。
STEP.3 始点から各頂点に対して高々2本の辺を使って到達できる最短経路を探す。
最短距離を更新する。
STEP.4 始点から各頂点に対して高々3本の辺を使って到達できる最短経路を探す。
最短距離を更新する。
.
. 高々\(n-1\)本になるまで繰り返す。(\(n\)は頂点数)
.
詳しい話は下の記事で解説しているのでここでは省略します。
簡単に説明すると最初は1本の辺だけを使って到達できる最短経路を探して、そこから使える辺の本数を1つずつ増やしていくと言う感じです。使ってもよい辺の本数が(頂点数-1)本までいったらこの操作を終了します。
負閉路がないグラフの場合は(頂点数-1)回の反復で始点から各頂点への最短距離を求めることができます。
なぜ(頂点数-1)回の反復で最短距離が求まるの?
結論から言うと各頂点への最短経路は必ず(頂点数-1)本の辺を使えば到達できるからです。下のグラフを使って説明したいと思います。
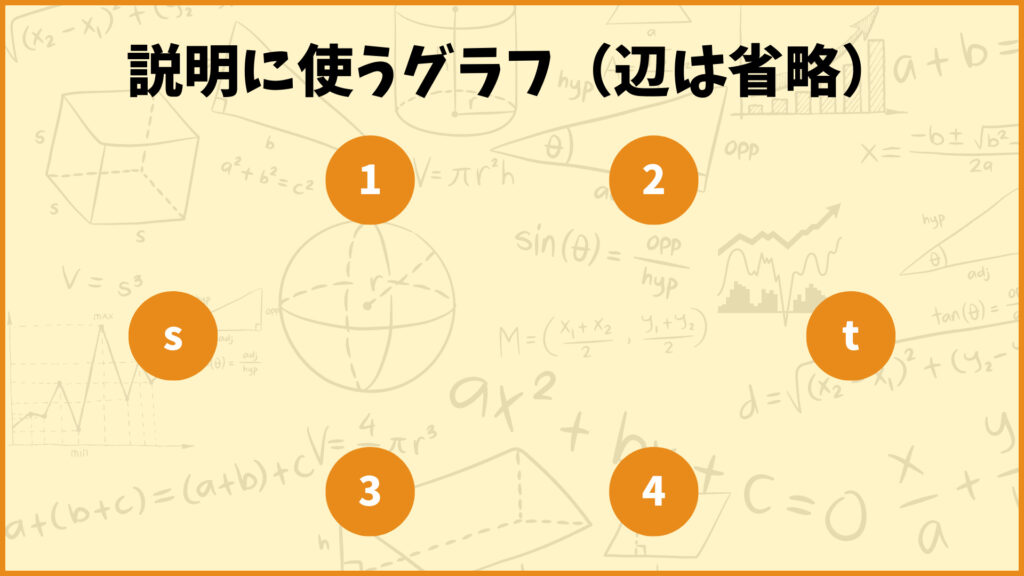
今頂点\(s\)から頂点\(t\)への最短経路を考えます。このときに辺を何本使うかに着目して考えてみます。
使う辺が1本の場合
まず最初に使う辺が1本のときを考えてみましょう。この場合は頂点\(s\)から頂点\(t\)へ直接向かう経路が最短経路になります。

使う辺が2本の場合
次に使う辺が2本の場合を考えてみましょう。このときは頂点\(s\)から他の頂点を1つ中継して頂点\(t\)に向かうルートが最短経路となります。
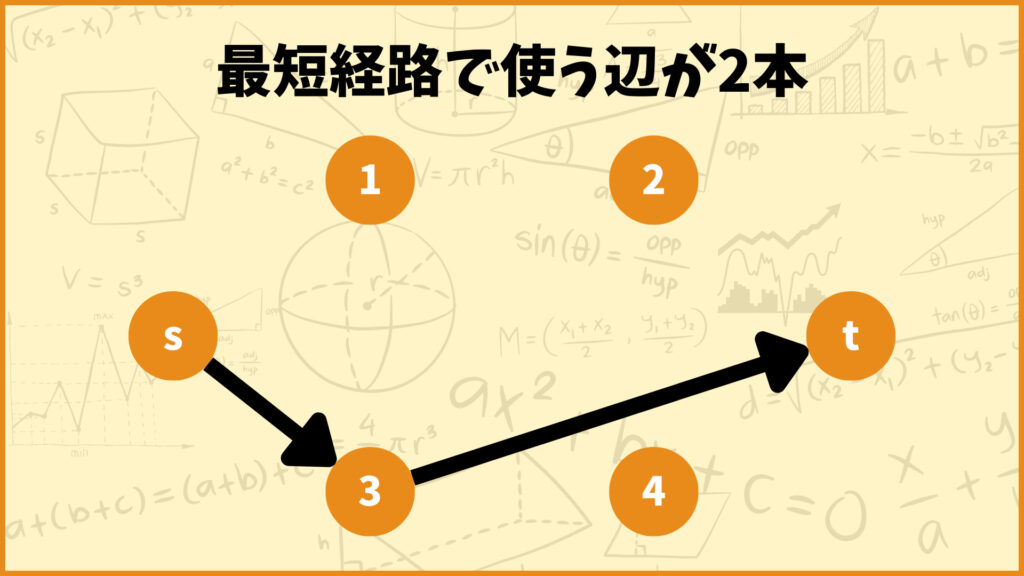
上の例では頂点3を経由させています。ここで重要なのは
「1つの頂点を中継している」
ということです。
使う辺が3本の場合
次に使う辺が2本の場合を考えてみましょう。このときは頂点\(s\)から他の頂点を2つ中継して頂点\(t\)に向かうルートが最短経路となります。
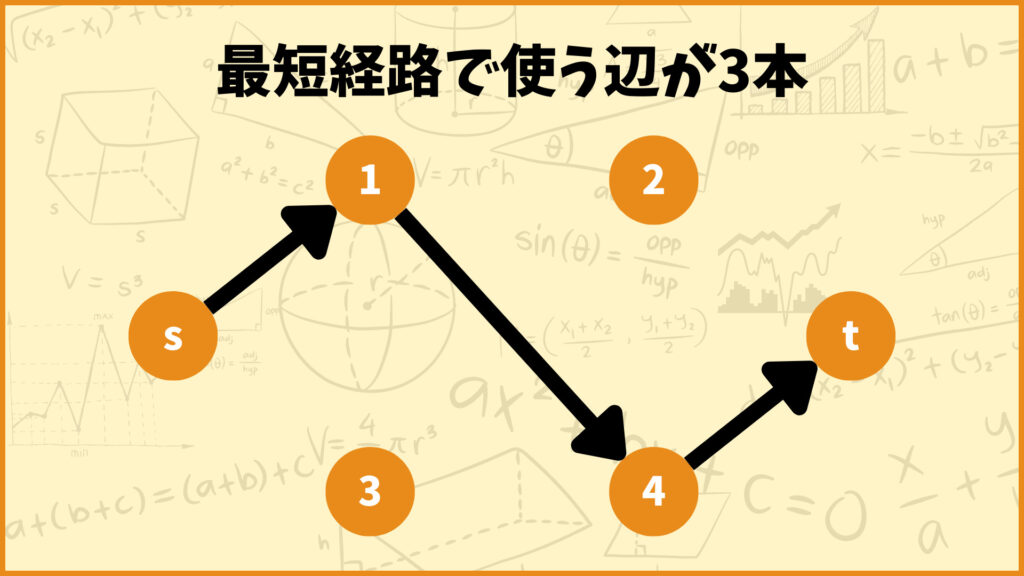
上の例では頂点1と頂点4を経由させています。ここで重要なのは
「2つの頂点を中継している」
ということです。
使う辺が4本の場合
次に使う辺が4本の場合を考えてみましょう。このときは頂点\(s\)から他の頂点を3つ中継して頂点\(t\)に向かうルートが最短経路となります。
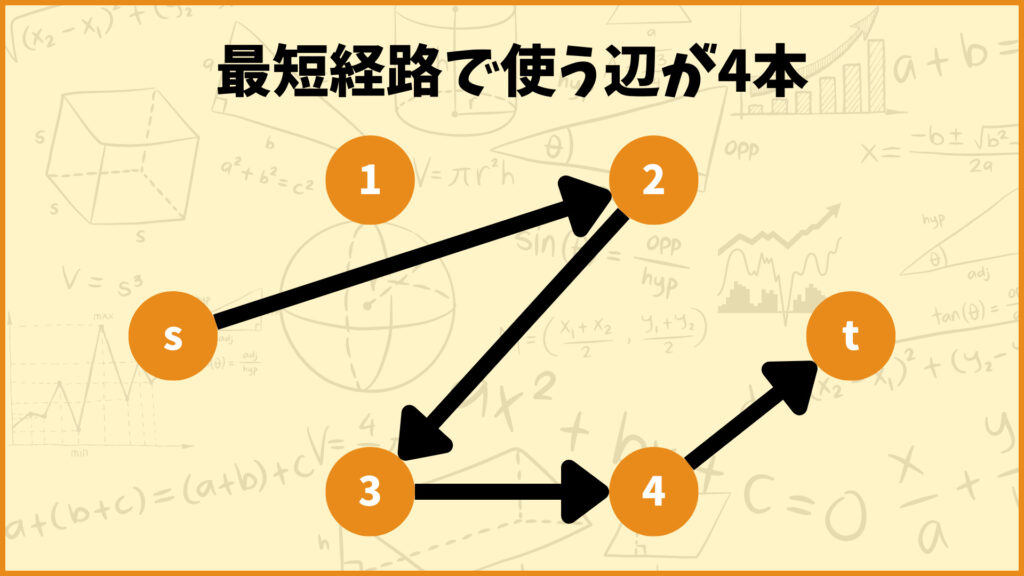
上の例では頂点2と頂点3と頂点4を経由させています。ここで重要なのは
「3つの頂点を中継している」
ということです。
使う辺が5本の場合
次に使う辺が2本の場合を考えてみましょう。このときは頂点\(s\)から他の頂点を4つ中継して頂点\(t\)に向かうルートが最短経路となります。
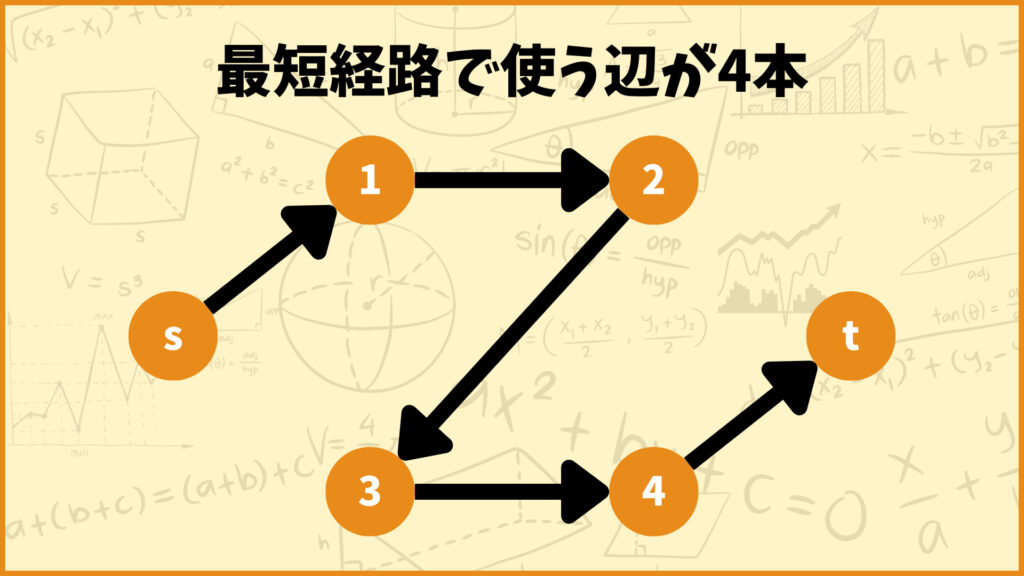
上の例では頂点1、頂点2、頂点3、頂点4を経由させています。ここで重要なのは
「4つの頂点を中継している」
ということです。
(頂点数-1)本の辺を使えば全ての頂点をたどれる
上の例を見ると分かるように(頂点数-1)本の辺を使えば全ての頂点をたどることができます。後の章で説明しますが同じ頂点を2回中継するルートは負閉路を持つので、負閉路を持たない場合必ず高々(頂点数-1)本の辺を使って構成できる最短経路が存在します。
ベルマンフォード法では(頂点数-1)回の反復で高々(頂点数-1)本の辺を使うときの最短距離を求められるので(頂点数-1)回の反復で最短距離を求めることができるという訳です。
同じ頂点を2回中継するとどうなるの?
それでは最後に同じ頂点を2回中継する場合はどうなるのかについて説明します。もしこのような最短経路が存在すれば、(頂点数)本以上の辺を使った最短経路が存在することになって、ベルマンフォード法が使えなくなってしまいます。
結論から言うと同じ頂点を2回中継するルートは負閉路を持ちます。これも先ほどと同じ例を使って考えてみましょう。
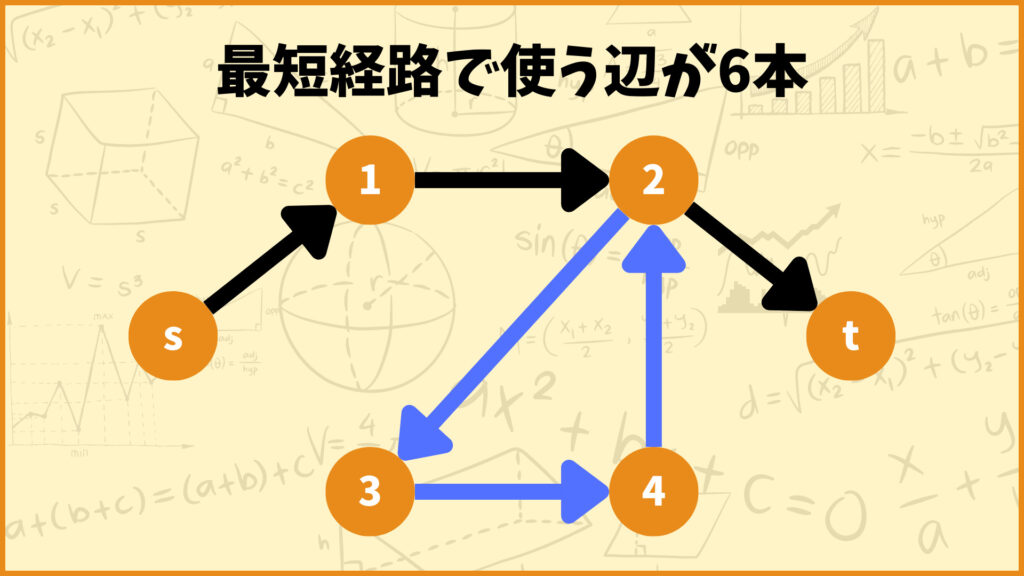
例えば上のルートが最短経路の場合を考えてみましょう。このルートは辺を6本使っており、
s → 1 → 2 → 3 → 4 → 2 → t
と頂点2を2回経由しています。
このとき上のルートは2 → 3 → 4 → 2の閉路を持ちます。また、この閉路を含まないs → 1 → 2 → tのルートは最短経路ではありません。これらの事実から2 → 3 → 4 → 2の閉路の重みの合計が負であることが分かります。
おわりに
いかがでしたか。
今回の記事ではベルマンフォード法について解説していきました。
今後もこのようなグラフ理論に関する記事を書いていきます!
最後までこの記事を読んでくれてありがとうございました。