こんにちは!しゅんです!
今回はクラスタリングとk平均法について解説していきたいと思います。
クラスタリングはデータをグループ分けすることです。またその手法の1つがk平均法です。ぼくがデータ分析の勉強をしていたときにでてきたので皆さんにもシェアしたいと思います!また今回は説明と一緒にpythonを使ってどんなものか確かめたいと思います。
それでは解説していきましょう!
普段はNBAのデータ分析をしたりしています。
ぜひこちらの記事も読んでみてください!
このブログでは経営工学を勉強している現役理系大学生が、経営工学に関することを色々話していきます!
ぼくが経営工学を勉強している中で感じたことや、興味深かったことを皆さんと共有出来たら良いなと思っています。
そもそも経営工学とは何なのでしょうか。Wikipediaによると
経営工学(けいえいこうがく、英: engineering management)は、人・材料・装置・情報・エネルギーを総合したシステムの設計・改善・確立に関する活動である。そのシステムから得られる結果を明示し、予測し、評価するために、工学的な分析・設計の原理・方法とともに、数学、物理および社会科学の専門知識と経験を利用する。
引用元 : 経営工学 – Wikipedia
長々と書いてありますが、要は経営、経済の課題を理系的な観点から解決する学問です。
クラスタリングってなに?
ザックリ説明するとクラスタリングは似てるデータを同じグループに分類することです。下の図を見てみましょう。
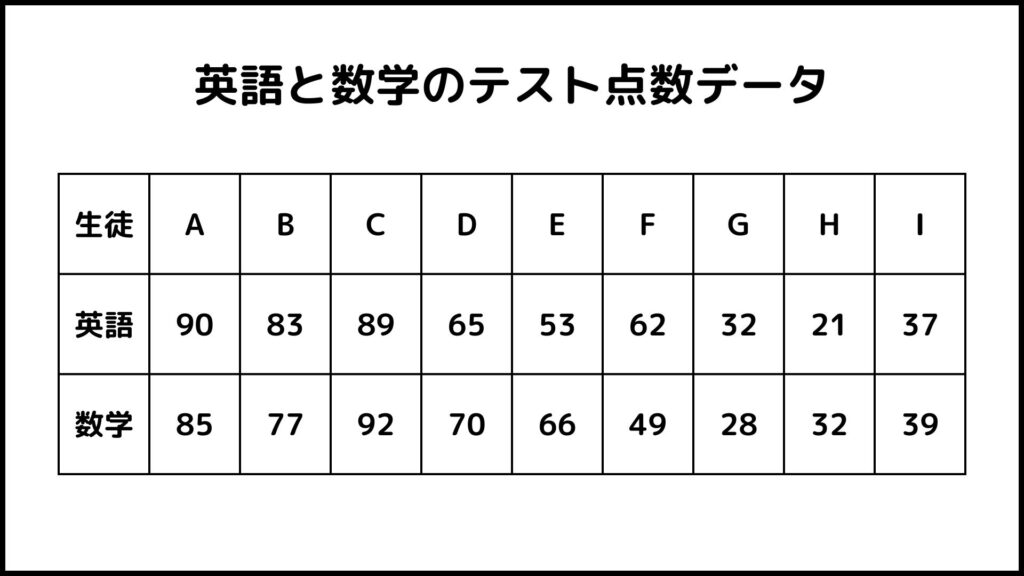
このデータはある学校における生徒9人の英語と数学のテスト点数のデータです。散布図にしてみてみましょう。
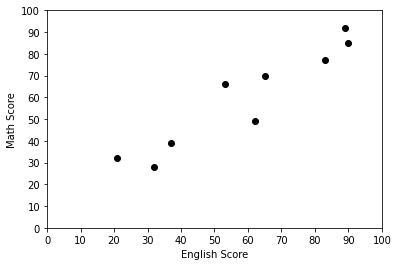
横軸が英語のテストで縦軸が数学のテストです。この散布図を見ると9つのデータを3つのグループに分けることができそうです。
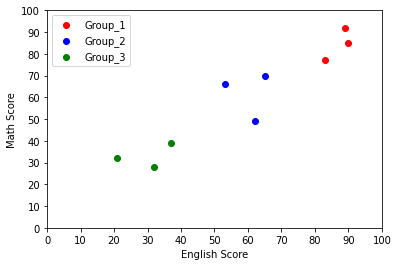
上のグラフのように赤、青、緑の3つのグループに分類できそうですね。このように似たようなデータを同じグループに分類することをクラスタリングと言います。
クラスタリングと判別分析の違い
クラスタリングの説明を聞いて、
これ判別分析に似てるな…
と思った人もいるかもしれません。どちらもデータを分類するという点で同じような分析をしています。それではこの2つの分析は何が違うのでしょう。
判別分析:
答えが事前に分かっている。
クラスタリング:
答えが事前に分かっていない。
判別分析は答えが事前に用意されているデータを分類するための手法です。例えば身長と体重のデータから性別を予測する判別分析を行うとします。このとき性別データは事前に分かっています。
このように答えが事前に用意されているなかで分析することを、機械学習の用語で教師あり学習と呼びます。
一方クラスタリングは答えが事前に用意されていません。
例えば上の例でいくと、各生徒がどのグループに属すかは分かっていません。グループがいくつあるのか、グループ名はなにか、などの情報が全くない状態からグループ分けをするのがクラスタリングです。
性別の判別分析では男、女というグループが事前に分かってました。
このように答えが事前に用意されていないなかで分析をすることを、機械学習の用語で教師なし学習と呼びます。
クラスタリングをpythonでやってみる
ということでここからは実際にpythonを使ってクラスタリングをやってみたいと思います。
クラスタリングにも色々種類がありますが、今回はk平均法を使った非階層的クラスタリングをやりたいと思います。
クラスタリングには階層的と非階層的なものがあります。
k平均法ってなに?
k平均法はクラスタリングをするために使われる手法の1つです。ザックリ言うとランダムにk個の中心点を作ってそこから近い順にグループ分けしていく手法です。
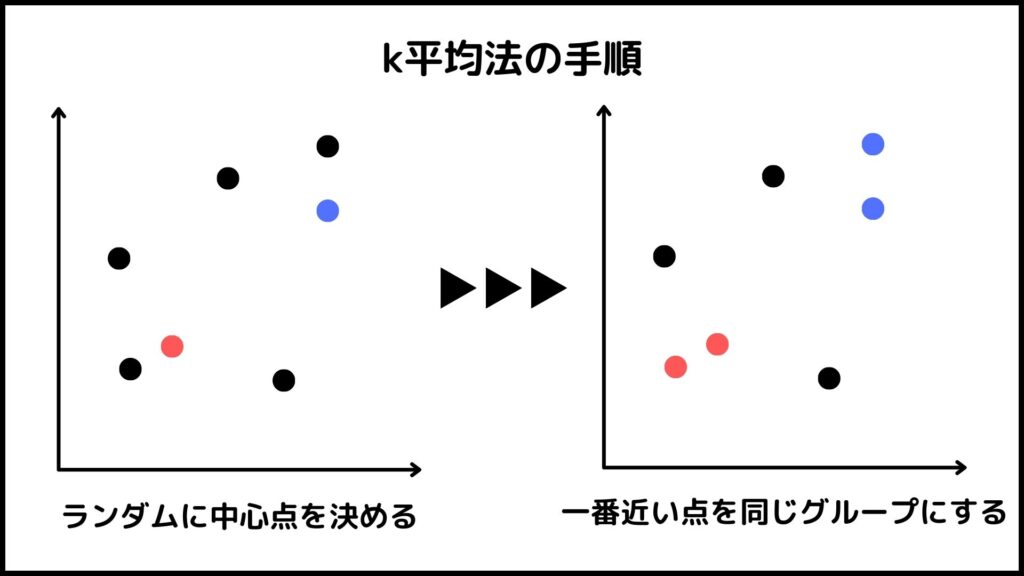
結果的にk個のグループができます。kは自分で決めることができ、データの特徴を把握して上手い具合に設定する必要があります。
今回の手順は以下の通りです。
今回はscikit-learnが提供しているデータセットを利用したいと思います。
クラスタリングとは関係ありませんが理解しやすいのでやります。
k平均法を使ってやりたいと思います。
グラフを使ってどのようなグループができたかを見てみます。
それではやってみましょう!
STEP.1 事前準備、データの作成
import pandas as pd # pandasをpdとしてインポート
import matplotlib.pyplot as plt # matplotlib.pyplotをpltとしてインポート
今回はデータを扱うためにpandas、グラフを作成するためにmatplotlibを使いたいと思います。これらはデータ分析をするときによく使うライブラリです。
as pdとすることでこれ以降pandasを使居たときはpdと省略できます。as pltも同様です。
次に今回使うデータをscikit-learnからインポートしましょう。scilit-learnが公開しているデータはいくつかありますが、今回はIris plants datasetを使いたいと思います。
Iris plants datasetは3種類のIrisという花に関するデータセットです。このデータセットにはsepal length(萼の長さ)、sepal width(萼の幅)、petal length(花弁の長さ)、petal width(花弁の幅)そしてそれぞれの花の種類データが入っています。3種類のIrisはIris-setosa, Iris-Versicolour, Iris-Virginicaという名前で、それぞれ0, 1, 2と番号付けされています。
# sikit-learnのデータ瀬戸からiris plants datasetをインポート
from sklearn.datasets import load_irisこのままだと分析に使えないので、使える形にしていきましょう。
df_X = pd.DataFrame(load_iris().data, columns=load_iris().feature_names)
df_y = pd.DataFrame(load_iris().target, columns = ["type"])
df = pd.concat([df_X, df_y], axis = 1)この説明をする前にまずは作成したデータ(df)の中身を見てみましょう。
df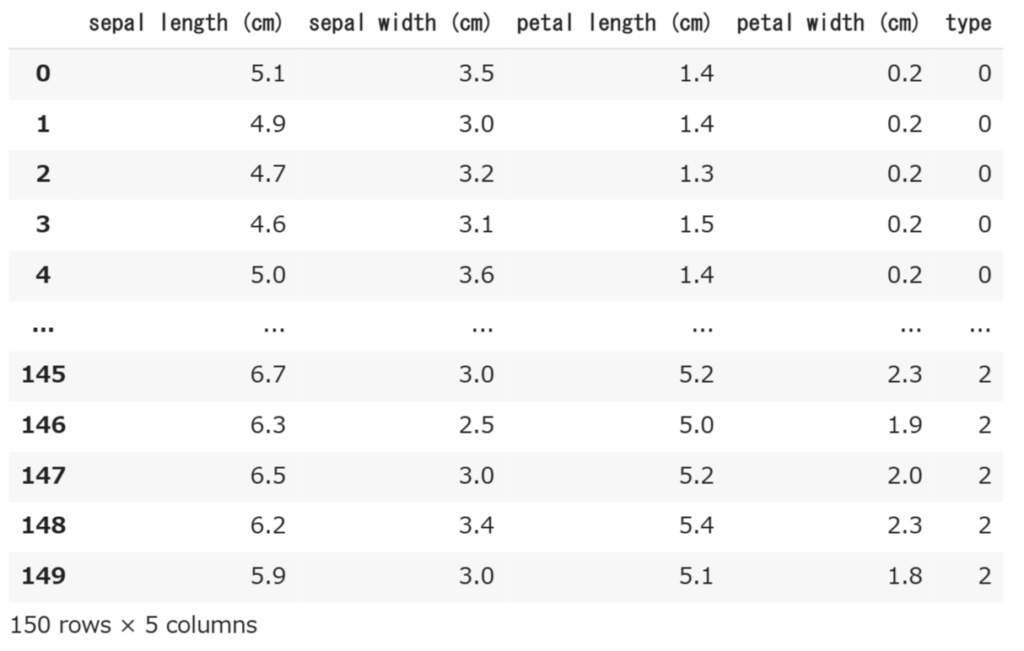
こんな感じの150行×5列のデータになっています。それではこの図を使って先ほどのコードについて解説します。
まず1行目ではsepal length (cm)からpetal width (cm)までのデータをデータフレームとしてdf_Xに格納しています。load_iris()の後ろに.dataを付けることでこれら4つのデータが取得でき、.feature_namesを付けることでsepal length (cm)などのデータの名前が取得できます。これらの名前を列名にしたいのでcolumnsに.feature_namesを入れています。
2行目は花の種類データに対して1行目と同じことをしています。irisの種類データは.targetで取得できます。また名前はtypeにしました。判別分析ではこれを答えとして分析を行いますが、今回行うのはクラスタリングなので使わないです。データセットの紹介のために見せています。
3行目は1行目と2行目で作成したデータフレームを結合しています。データフレームを結合する場合は.concat(結合したいデータ)で出来ます。 axisは結合方向を指定するもので、横方向に結合したい場合は1にします。
さきほども言いましたが、クラスタリングをするときには1行目のデータしか使わないので、2、3行目は飛ばしても大丈夫です。今回はデータセット説明のために花の種類データも使ってみました。さらに言えばこの種類データはクラスタリングによって求めたいものなので、普通はこのデータがない状態でクラスタリングを行います。
STEP.2 データの可視化
クラスタリングには直接関係ありませんが、matplotlibを使って散布図を作ってみましょう。
x = "sepal width (cm)" # 横軸にsepal width (cm)を使う
y = "petal width (cm)" # 縦軸にpetal width (cm)を使う
# 散布図の作成
plt.scatter(df[x],df[y], color = "black")
plt.xlabel(x)
plt.ylabel(y)
# 散布図の表示
plt.show()
ということで横軸にsepal width (cm)、縦軸にpetal width (cm)を使って作った散布図ができました。x,yを別の変数に変えると散布図も変わるはずです。
STEP.3 クラスタリングの実行
STEP.2で使用したsepal width (cm)とpetal width (cm)を使ってクラスタリングをしたいと思います。
本当は4種類のデータ全部を使ってクラスタリングするべきなのですが、それだと可視化するのが大変で分かりにくいので今回は2つしか使いません。
data = df[[x,y]] # クラスタリングに使用するデータを用意するdfの中でx, yだけを抽出しています。x, yはSTEP.2で定義したやつです。
それではk平均法を使ってクラスタリングを実行していきます。まずは準備をします。
# k平均法をインポート
from sklearn.cluster import KMeansk平均法は英語でk-meansと言います。日本語でもk-means法と書いてる記事をよく見かけます。
次に何個のグループに分けるかを決めてクラスタリングを実行します。今回利用するデータセットは3種類のIrisに関するものなので、グループの数も3つにするのが良さそうです。
kmeans = KMeans(n_clusters=3, random_state=0) # グループ数を3に指定
kmeans.fit(data) # k平均法の実行k平均法の結果にkmeansと名前を付けました。kmeansの後ろに.fit()を付ければk平均法によるクラスタリングを実行することができます。
n_clustersの所でグループ数を何個にするか設定できます。random_stateはどの点を最初の中心点にするかを設定できます。入れる数字によって結果が変わるのでぜひやってみてください。
ということでクラスタリングが実行できました。結果は.labels_で取得できます。
# 結果を表示
print(kmeans.labels_)
3つのグループはそれでぞれ0, 1, 2の数字に変換されています。同じ数字が同じグループです。
それでは散布図にしてみましょう。
# 散布図の作成
plt.scatter(df[x],df[y], c=kmeans.labels_, cmap="tab10") # グループによって色分けをする
plt.xlabel(x)
plt.ylabel(y)
# 散布図の作成
plt.show()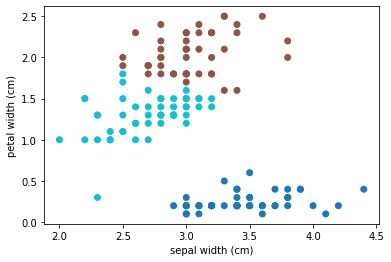
ということでグループごとに色分けした結果がこちらです。なんとなくちゃんと分類できてそうですね。
本来クラスタリングは教師なし学習なのでこの結果が合っているのかはよく分かりません。しかし今回はtypeに実際の答えがあるのでどれくらい合っているのかを確かめられます。
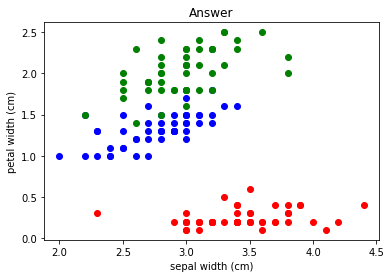
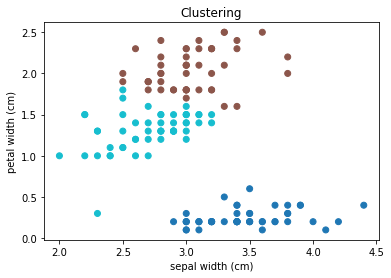
左図が実際の答えで右図がクラスタリングによる結果です。大体あってそうですが、境界部分で間違ったグループ分けがされていますね。
実際に何個あっているか計算してみました。

150個中139個正解していて、正答率は約93%でした。結構正答率高そうですね。
※実際のクラスタリングでは答えが無いので正答率を計算するのは難しいです。
おわりに
いかがでしたでしょうか。
今回の記事ではpythonを使ってクラスタリングについて説明していきました。こんな感じでプログラミングを使えばいろいろなことができます。非常に興味深いですよね。
データの数値をいじるとまた違う結果が得られるので興味がある人はぜひやってみてください!またこの記事ではクラスタリングの中でも非階層的クラスタリングについて説明しました。他にも色々な手法があるので是非調べてやってみてください!
これからもこのようにプログラミングで色々やっていきたいと思います。ぼくが一番勉強になるので続けていきたいです!
最後までこの記事を読んでくれてありがとうございました。
この記事が役に立ったら幸いです。





