- グラフの離心数、半径、直径、中心ってなに？
- グラフの離心数、半径、直径、中心の計算方法は？
- 具体例を使ってこれらの4つを理解したい…
離心数
無向グラブ\(G=(V,E)\)と正の辺の長さが与えられたとき、各頂点\(v\)に対して離心数\(\epsilon (v)\)を以下のように定義する
\(\epsilon (v) = \displaystyle{\max_{w \in V} d(v,w)}\)
※但し\(d(v,w)\)は最短\(v-w\)路の長さ
半径
\( \displaystyle{\min_{v \in V}\epsilon(v)}\)
直径
\( \displaystyle{\max_{v \in V}\epsilon(v)}\)
中心
半径を定義する頂点
こんにちは！しゅんです！
今回の記事ではグラフの離心数・半径・直径・中心について解説していきます！
これらはグラフ理論で登場する用語で、グラフの特徴を把握するときに使うことができます。
ということでこの記事ではグラフの離心数・半径・直径・中心がどんなものか、そしていくつかグラフを使ってこれら4つの値を求めていきたいと思います！
\\\ pythonで離心数を求める記事はこちらから！ ///
普段は組合せ最適化の記事を書いてたりします。
ぜひ他の記事も読んでみてください！
このブログの簡単な紹介はこちらに書いてあります。
興味があったら見てみてください。
このブログでは経営工学を勉強している現役理系大学生が、経営工学に関することを色々話していきます！
ぼくが経営工学を勉強している中で感じたことや、興味深かったことを皆さんと共有出来たら良いなと思っています。
そもそも経営工学とは何なのでしょうか。Wikipediaによると
経営工学（けいえいこうがく、英: engineering management）は、人・材料・装置・情報・エネルギーを総合したシステムの設計・改善・確立に関する活動である。そのシステムから得られる結果を明示し、予測し、評価するために、工学的な分析・設計の原理・方法とともに、数学、物理および社会科学の専門知識と経験を利用する。
引用元 : 経営工学 – Wikipedia
長々と書いてありますが、要は経営、経済の課題を理系的な観点から解決する学問です。
離心数・半径・直径・中心を説明してみた
離心数ってなに？
グラフの半径・直径・中心は離心数というものを使って定義されるので、まずはこの離心数の説明をします。
無向グラブ\(G=(V,E)\)と正の辺の長さが与えられたとき、各頂点\(v\)に対して離心数\(\epsilon (v)\)を以下のように定義する
\(\epsilon (v) = \displaystyle{\max_{w \in V} d(v,w)}\)
※但し\(d(v,w)\)は最短\(v-w\)路の長さ
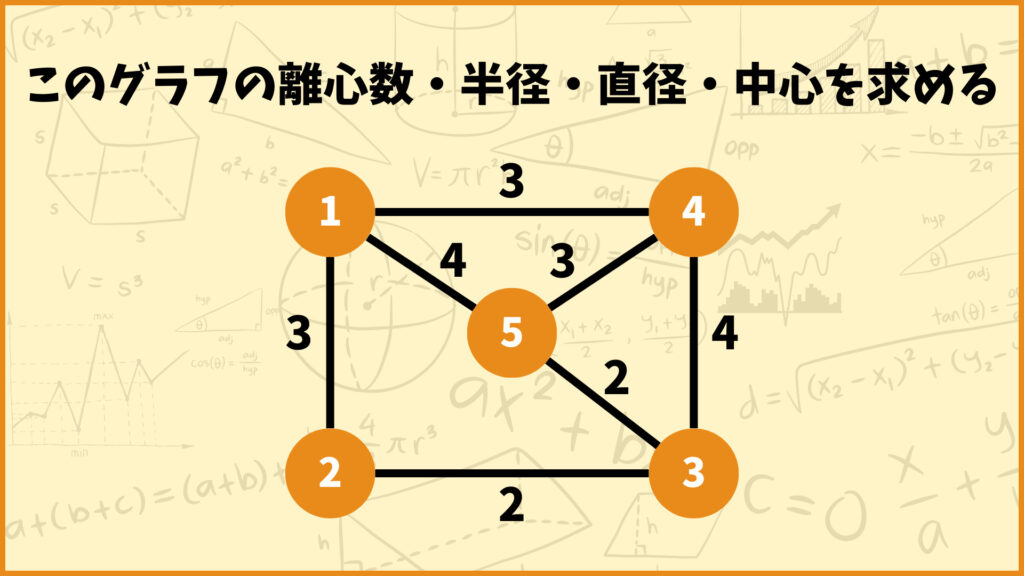
これだけ見ても何言ってるかよく分からないので、具体例を使って1つずつ説明していきます。例えば下のグラフについて考えてみましょう。
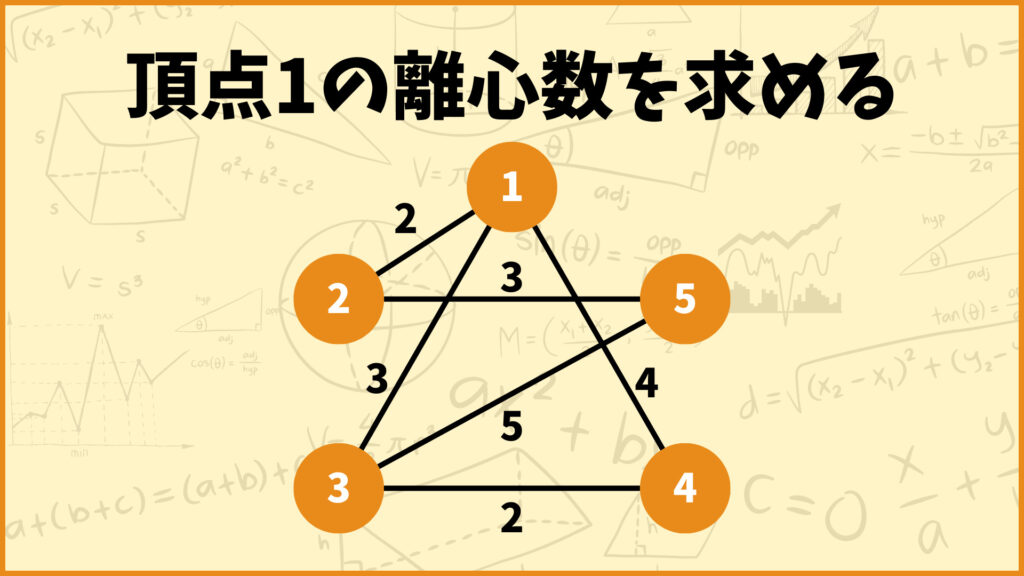
上のグラフに関して頂点1の離心数\(\epsilon(1)\)を求めていきましょう。離心数の定義によると、頂点1から他の頂点\(w\)への最短距離\(d(1,w)\)を求めて、その中から最も値が大きいものを選びます。
ということで頂点2～頂点5それぞれに対して最短距離を求めた結果下のようになりました。
\(d(1,2) = 2\) (頂点1→頂点2)
\(d(1,3) = 3\) (頂点1→頂点3)
\(d(1,4) = 4\) (頂点1→頂点4)
\(d(1,5) = 5\) (頂点1→頂点2→頂点5)
この中での最大値が離心数になるので、頂点1の離心数は
\(\epsilon(1) = 5\)
という風に求めることができます。他の頂点についても同じように離心数を求めることができます。
半径ってなに？
それでは今定義した離心数を使って半径を定義しましょう。
\( \displaystyle{\min_{v \in V}\epsilon(v)}\)
この式は「各頂点の離心数の中で最小のモノを持ってくる」ということを表しています。これも先ほどの具体例を使って説明します。
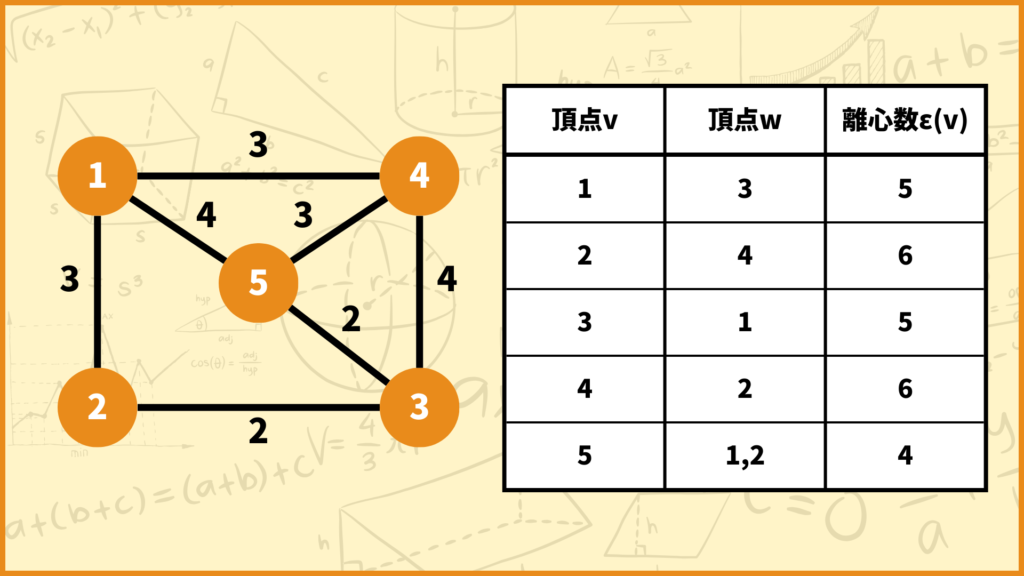
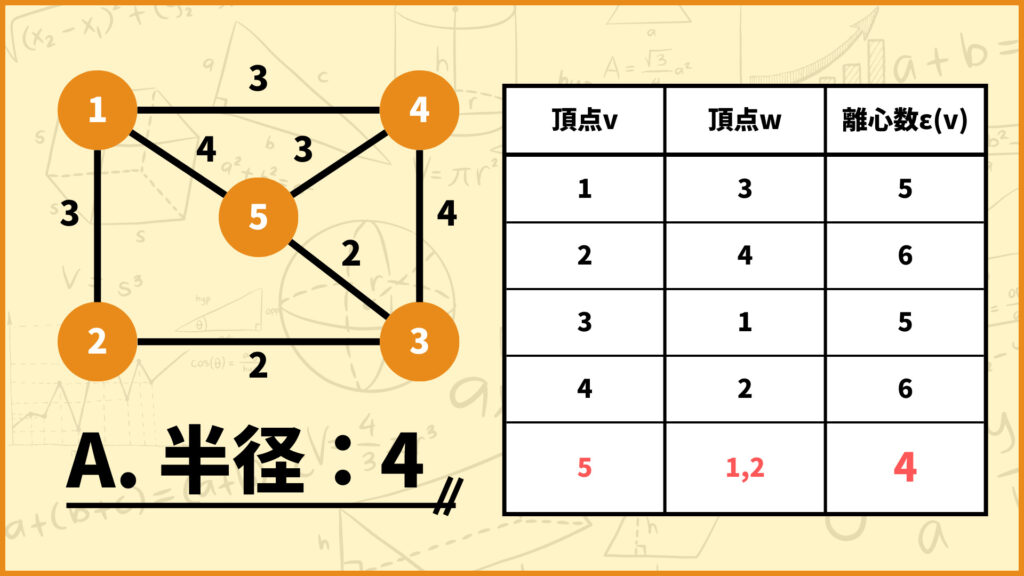
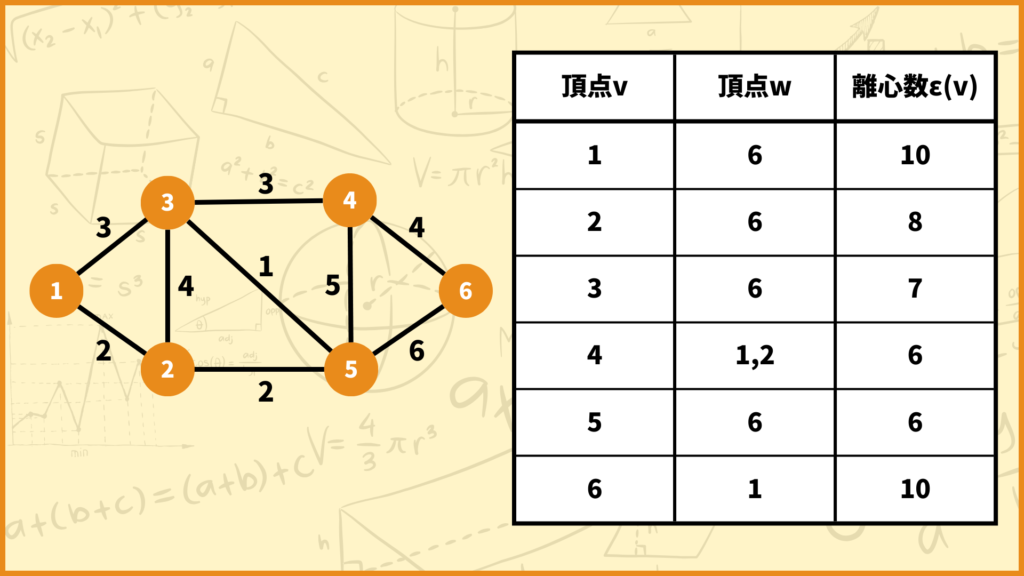
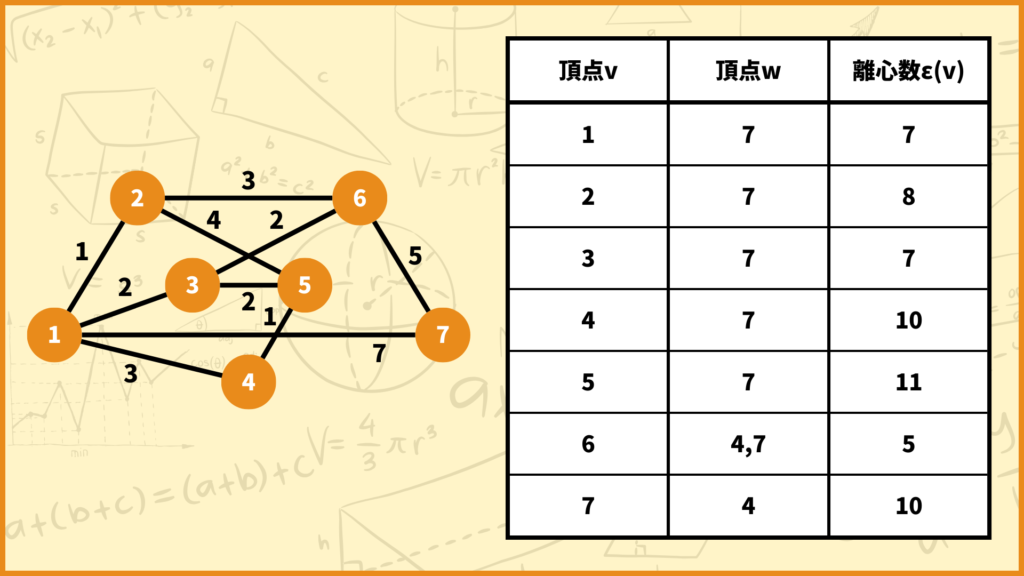
上のグラフの離心数を、全ての頂点に対して求めて表にまとめてみました。例えば頂点2の離心数は6で、頂点2から頂点4へと向かうパスの最短距離が\(d(2,4)=6\)だということです。
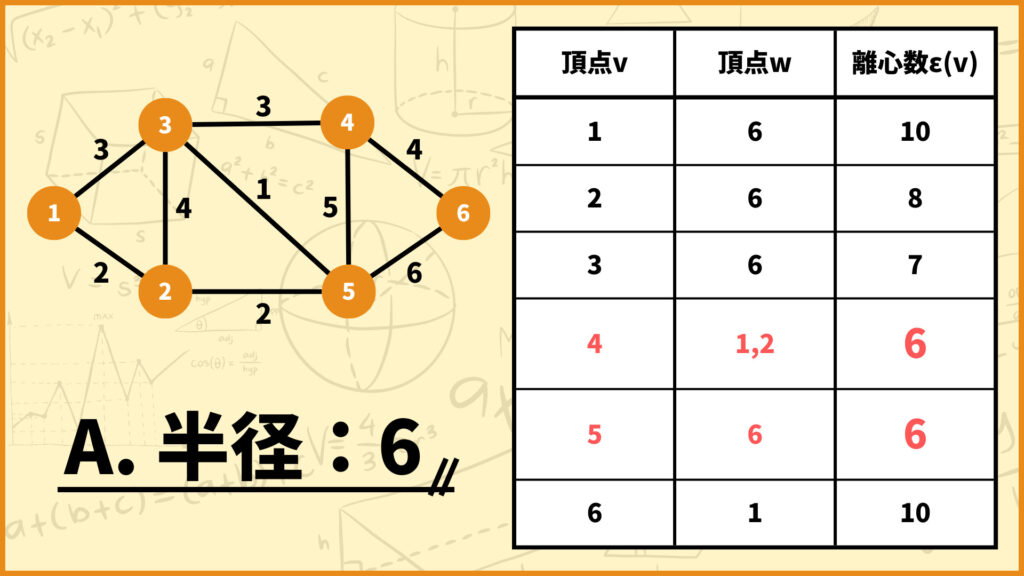
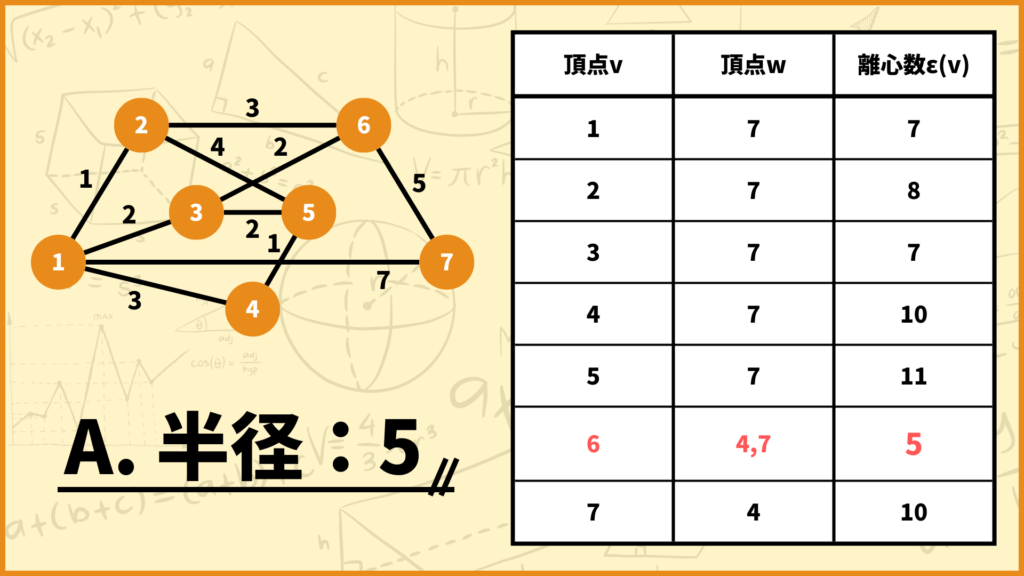
半径は一番右列の離心数\(\epsilon(v)\)の中で最も小さいモノなので、このグラフの半径は5となります。
直径ってなに？
次に離心数を使って直径を定義しましょう。
\( \displaystyle{\max_{v \in V}\epsilon(v)}\)
この式は「各頂点の離心数の中で最大のモノを持ってくる」ということを表しています。これも先ほどの具体例を使って説明します。
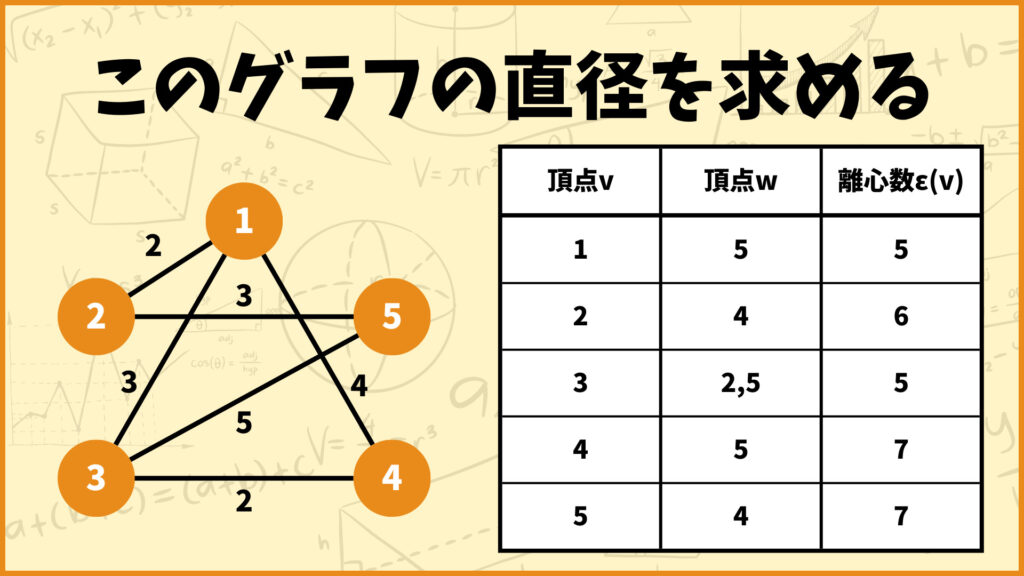
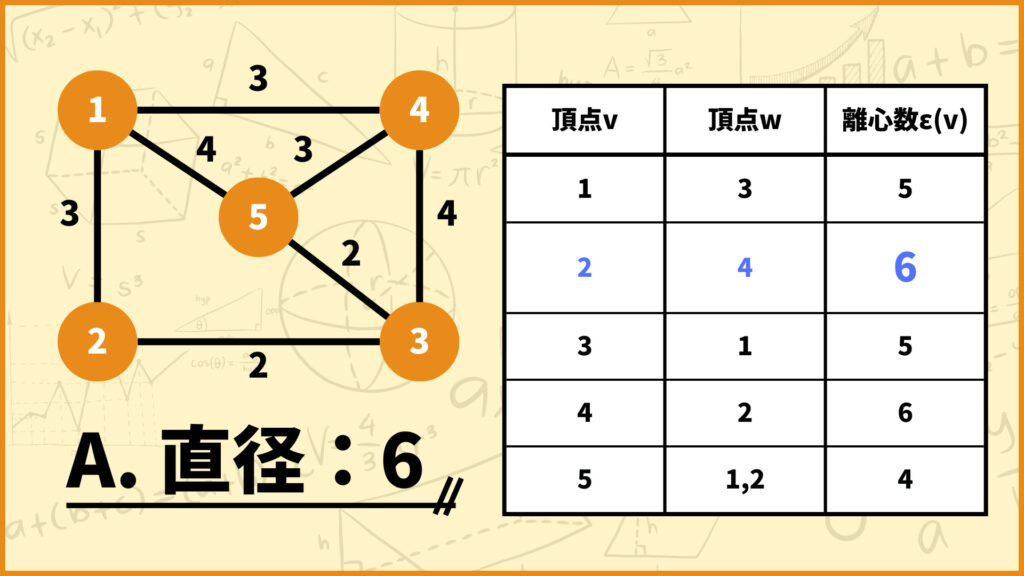
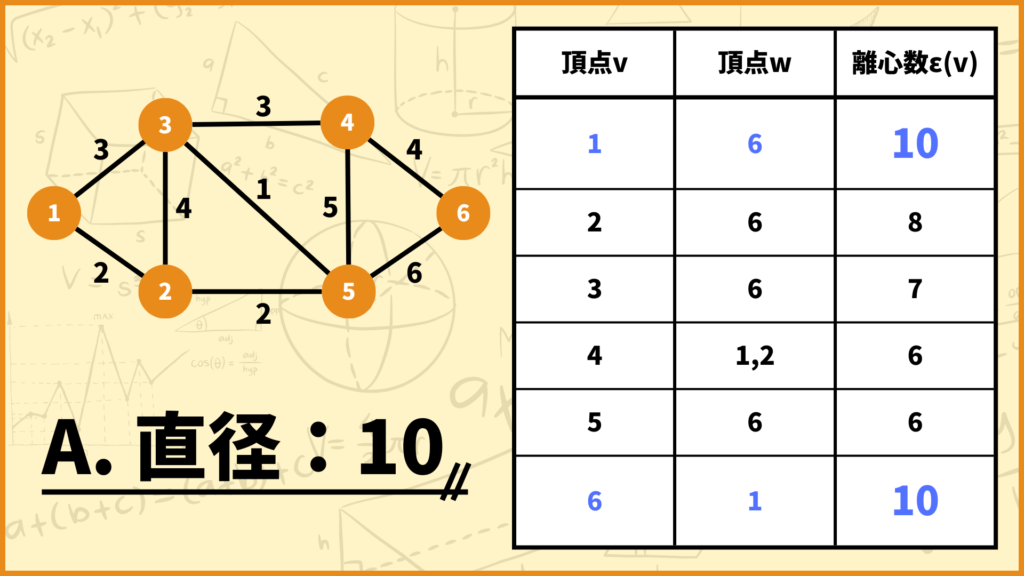
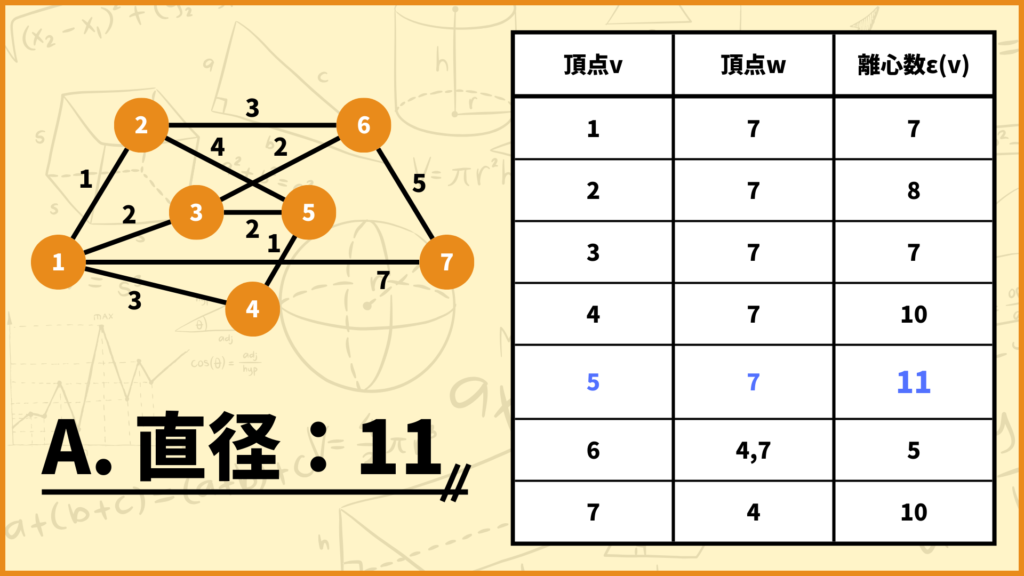
半径の説明の時に使った表をまた使います。直径は一番右列の離心数\(\epsilon(v)\)の中で最も大きいモノなので、このグラフの直径は7となります。
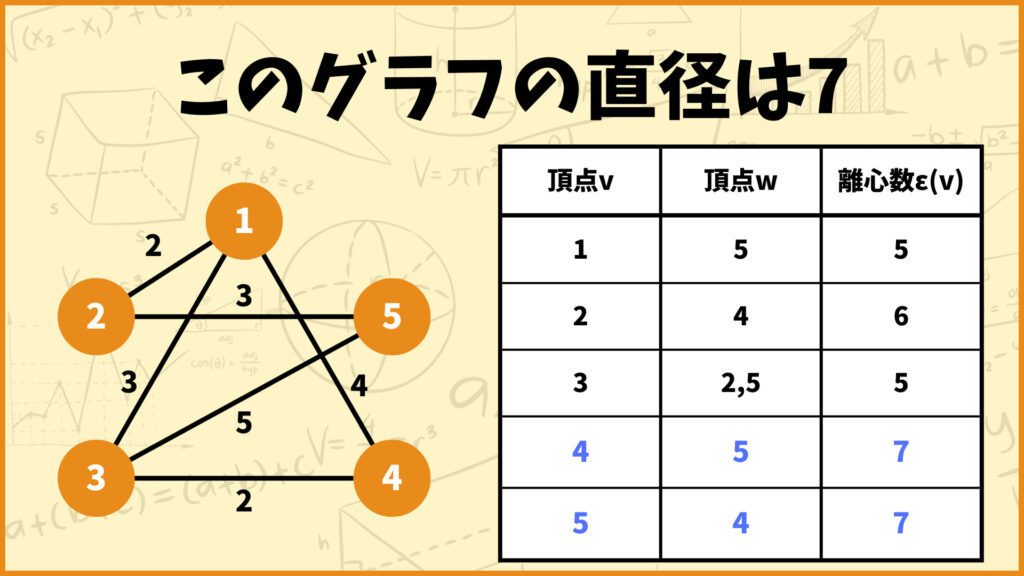
中心ってなに？
最後に中心の説明をしたいと思います。
半径を定義する頂点
これは言葉で定義されていますね。今までと同じように具体例を使って説明します。
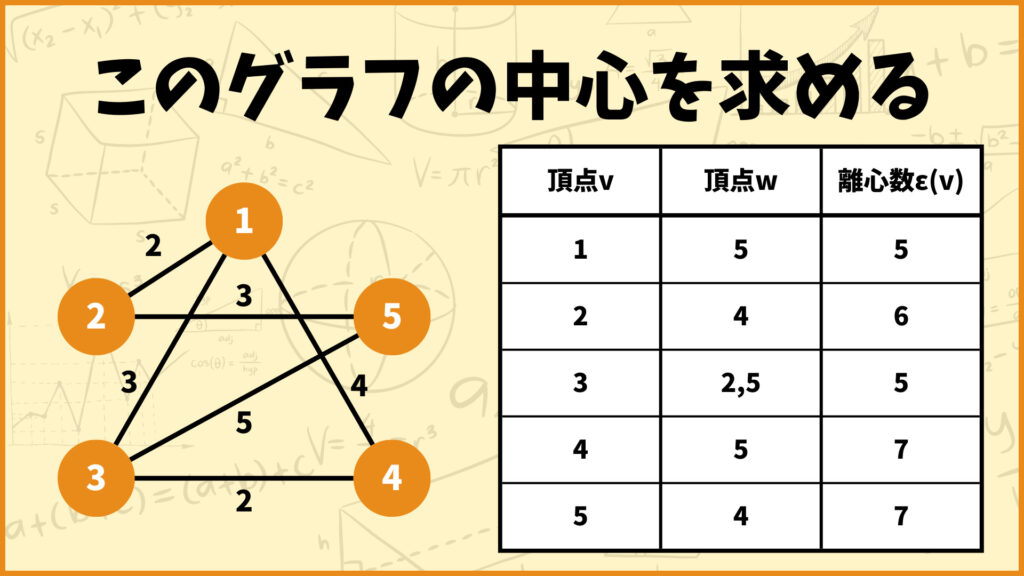
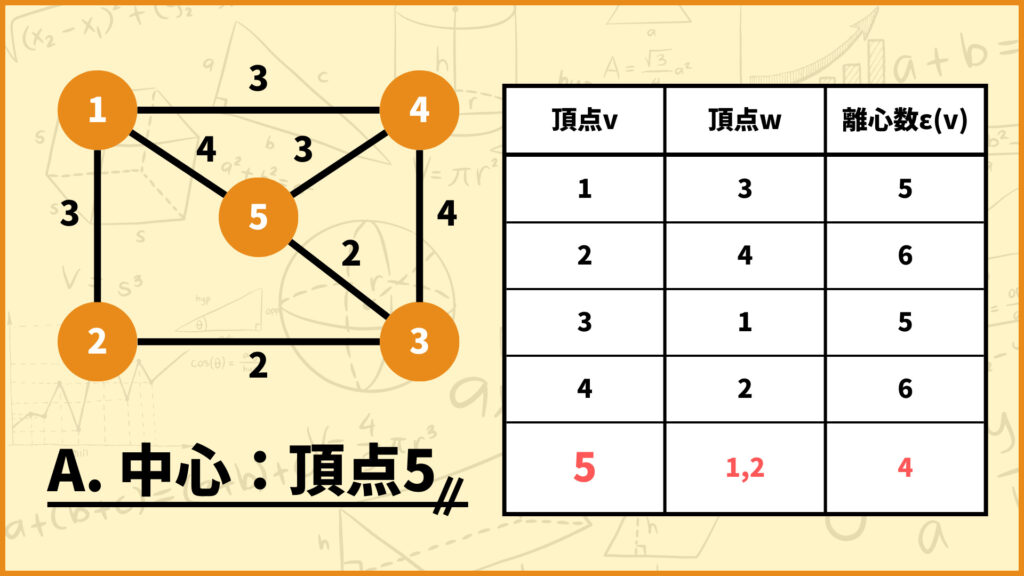
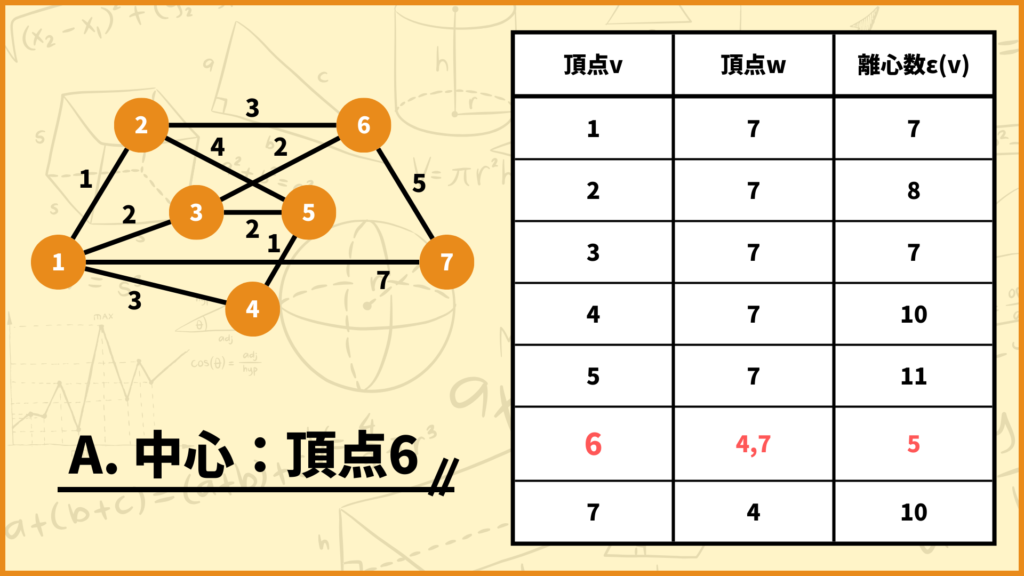
半径の説明の所で、このグラフの半径は5だと言うことが分かりました。これって「各頂点の離心数の中で、頂点1と頂点3の離心数が最も小さいから半径は5ですよ」ってことでしたね。
これら2頂点はこのグラフの半径を定義する頂点なので、中心は頂点1と頂点3になります。
一般に中心は複数個存在します。
半径・直径・中心は何を表しているの？
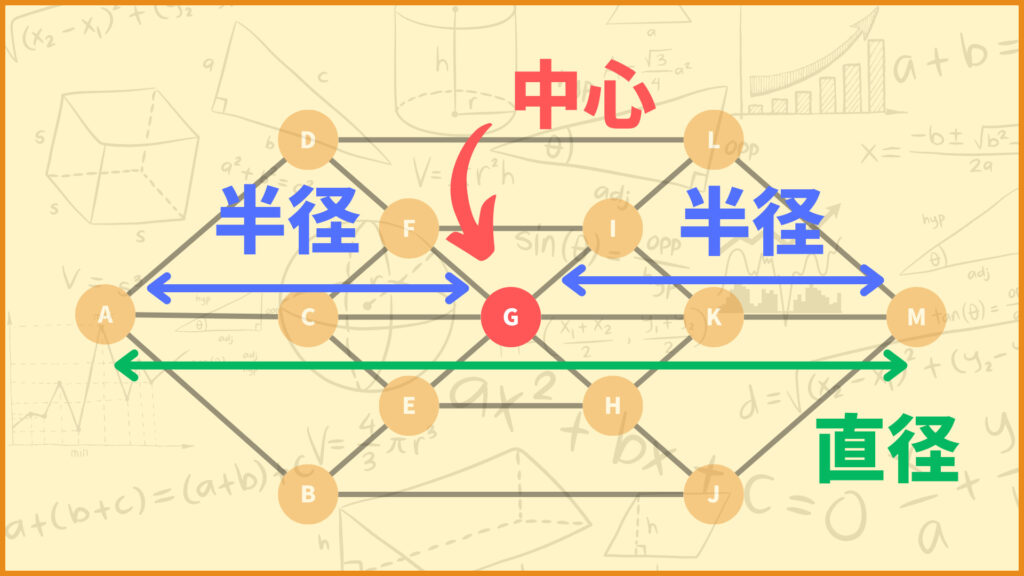
ここまでは半径・直径・中心の定義についてそれぞれ説明しましたが、これらは一体何を表しているのでしょうか。それを理解するために以下のようなグラフを考えます。
このグラフの頂点は二次元座標で位置が設定されていて、辺長はユークリッド距離で定義されています。
ユークリッド距離：
2点\(a = (x_1,y_1),b = (x_2,y_2)\)の間のユークリッド距離は
\(d(a,b) = \sqrt{(x_1 – x_2)^2 + (y_1 – y_2)^2}\)
で定義される。
このグラフの各頂点に対して離心数を計算した結果は以下の通りです。(pythonで計算しました。)
これを見ると頂点Gの離心数が一番小さくて、頂点A,Mの離心数がいちばん大きいことが分かります。すなわちこのグラフの半径は4、直径は8、中心は頂点Gとなります。
次に各頂点を色分けしてみましょう。中心である頂点Gからの距離が等しい点で色分けした結果以下のようになりました。
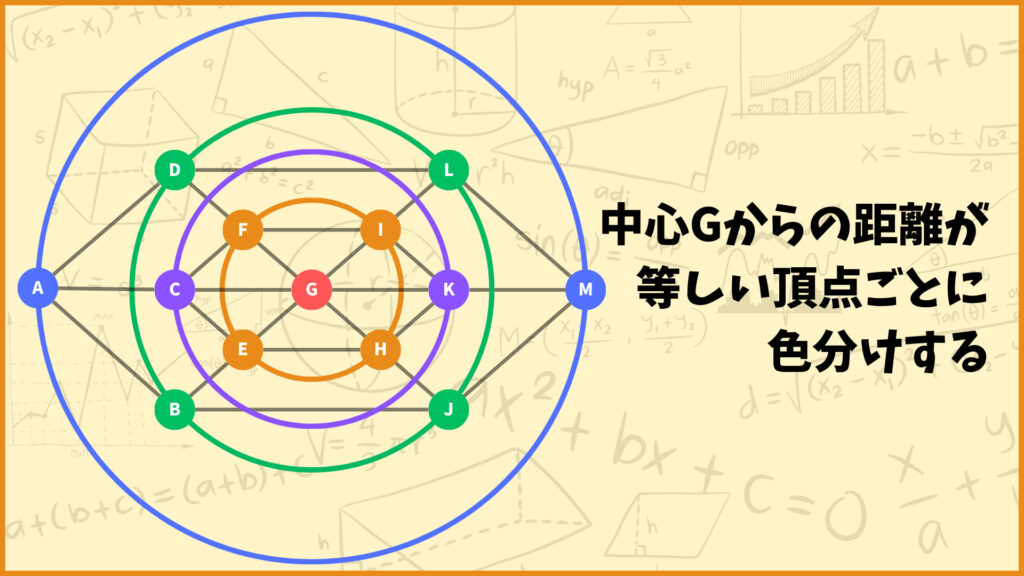
このとき一番外側の青い円の半径がこのグラフの半径、青い円の直径がこのグラフの直径に対応していますね。このように考えるとグラフの半径・直径・中心を理解しやすいと思います。
\\\ pythonで離心数を求める記事はこちらから！ ///
離心数・半径・直径・中心を計算する
それでは3つの具体例を使って実際に離心数・半径・直径・中心を計算してみましょう。
問題.1
問題.2
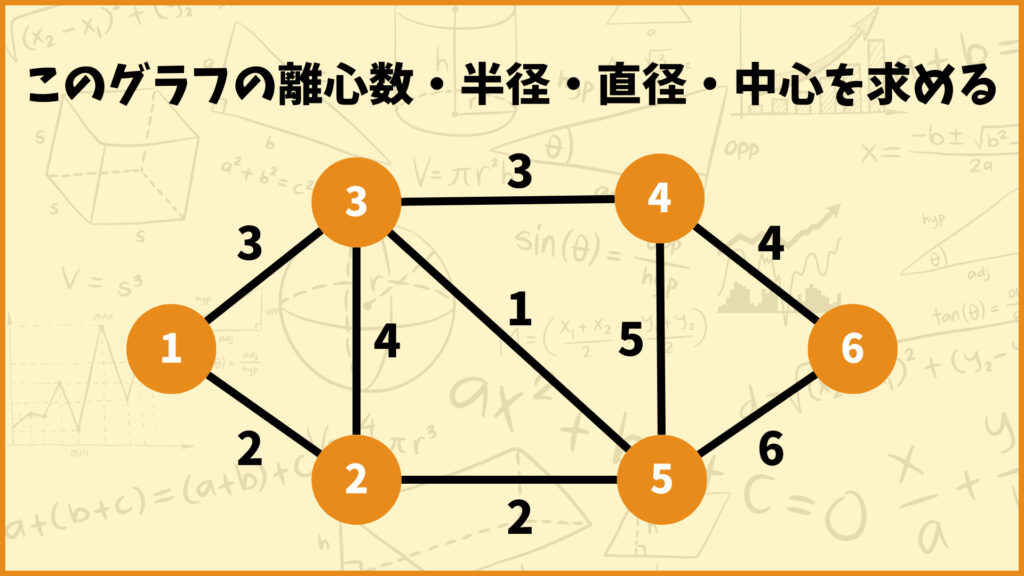
問題.3
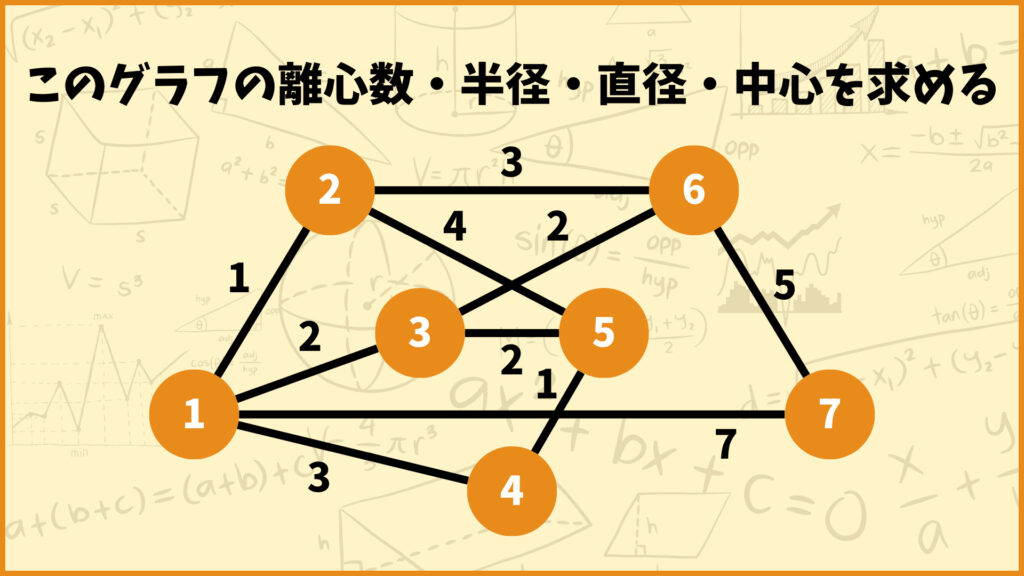
おわりに
いかがでしたか。
今回の記事ではグラフの離心数・半径・直径・中心について解説していきました。
今後もこのような離散数学に関する記事を書いていきます！
最後までこの記事を読んでくれてありがとうございました。
