こんにちは!しゅんです!
この記事ではpythonでワーシャルフロイド法を実装する方法を解説しています。
ワーシャルフロイド法はグラフが与えられたときに全ての2頂点間の最短距離を求めるアルゴリズムです。
ワーシャルフロイド法の手順はこちらの記事で詳しく解説しています!
それではやっていきましょう!
普段は組合せ最適化の記事を書いてたりします。
ぜひ他の記事も読んでみてください!
このブログの簡単な紹介はこちらに書いてあります。
興味があったら見てみてください。
このブログでは経営工学を勉強している現役理系大学生が、経営工学に関することを色々話していきます!
ぼくが経営工学を勉強している中で感じたことや、興味深かったことを皆さんと共有出来たら良いなと思っています。
そもそも経営工学とは何なのでしょうか。Wikipediaによると
経営工学(けいえいこうがく、英: engineering management)は、人・材料・装置・情報・エネルギーを総合したシステムの設計・改善・確立に関する活動である。そのシステムから得られる結果を明示し、予測し、評価するために、工学的な分析・設計の原理・方法とともに、数学、物理および社会科学の専門知識と経験を利用する。
引用元 : 経営工学 – Wikipedia
長々と書いてありますが、要は経営、経済の課題を理系的な観点から解決する学問です。
ワーシャルフロイド法の手順
ワーシャルフロイド法の手順は以下のようになります。
記号の定義
\(G = (V,E)\):有向グラフ
\(d_{ij}^{(k)}\):頂点集合\(V\)の部分集合\(\{1,2,…,k\}\)のみを通れるときの、頂点\(i\)から頂点\(j\)への最短距離
アルゴリズムの手順
STEP 0 グラフの重み付き隣接行列を用意する(最短距離の初期値\(d_{ij}^{(0)}\)の設定)
STEP 1 \(k = 1\)とし、全ての\(i,j \in V\)に対して\(d_{ij}^{(1)}\)を以下のように更新する。
\(d_{ij}^{(1)} = \min\{d_{ij}^{(0)}, d_{i1}^{(0)} + d_{1j}^{(0)}\}\)
STEP 2 \(k = 2\)とし、全ての\(i,j \in V\)に対して\(d_{ij}^{(2)}\)を以下のように更新する。
\(d_{ij}^{(2)} = \min\{d_{ij}^{1)}, d_{i2}^{(1)} + d_{1j}^{(1)}\}\)
STEP 3 \(k = 3\)とし、全ての\(i,j \in V\)に対して\(d_{ij}^{(3)}\)を以下のように更新する。
\(d_{ij}^{(3)} = \min\{d_{ij}^{(2)}, d_{i3}^{(2)} + d_{3j}^{(2)}\}\)
・
・
・
STEP n \(k = n\)とし、全ての\(i,j \in V\)に対して\(d_{ij}^{(n)}\)を以下のように更新する。
\(d_{ij}^{(n)} = \min\{d_{ij}^{(n-1)}, d_{in}^{(n-1)} + d_{nj}^{(n-1)}\}\)
ワーシャルフロイド法の手順はこちらの記事で詳しく解説しています!
ワーシャルフロイド法をpythonで実装する
入力:重み付き隣接行列
出力:\((i,j)\)成分が頂点\(i\)から頂点\(j\)への最短距離となる行列
今回は入力を「重み付き隣接行列」とします。結論以下のコードでワーシャルフロイド法を実装することができます。
## ワーシャルフロイド法を関数として定義する
def floyd_warshall(D): # 重み付き隣接行列を入力とする
n = len(D) # 行列のサイズをnとする
for k in range(n):
D_next = [[0 for _ in range(n)] for _ in range(n)] # 各ステップでの計算で求めた値を保持する行列を設定する
for i in range(n):
for j in range(n):
# 行列の各成分の値を更新する
if D[i][j] > D[i][k] + D[k][j]:
D_next[i][j] = D[i][k] + D[k][j]
else:
D_next[i][j] = D[i][j]
D = D_next
return D # (i,j)成分が頂点iから頂点jへの最短距離となる行列を返すinf = 10000000 # ∞を設定する
D = [[inf,1,-2,inf,inf],[inf,inf,inf,5,1],[4,3,inf,inf,4],[inf,inf,-4,inf,-2],[inf,inf,inf,3,inf]] # 重み付き隣接行列
print(floyd_warshall(D)) #結果を返す
このコードを実行したら上のような結果が得られました。とは言っても文字だけじゃよく分からないので1つずつ解説していきます。
関数として定義する
## ワーシャルフロイド法を関数として定義する
def floyd_warshall(D): # 重み付き隣接行列を入力とする
n = len(D) # 行列のサイズをnとする今回はワーシャルフロイド法を関数として定義しました。関数の名前はfloyd_warshallとしました。(名前は何でもOKです)このコードの意味は
「floyd_warshallは引数(入力される値)がDの関数である」
です。
n = len(D)で入力される行列Dのサイズを取得しています。仮に\(4 \times 4\)の行列が入力されたらn = 4となります。
行列の各成分の値を更新する
for k in range(n):
D_next = [[0 for _ in range(n)] for _ in range(n)] # 各ステップでの計算で求めた値を保持する行列を設定する
for i in range(n):
for j in range(n):
# 行列の各成分の値を更新する
if D[i][j] > D[i][k] + D[k][j]:
D_next[i][j] = D[i][k] + D[k][j]
else:
D_next[i][j] = D[i][j]
D = D_next
この部分では行列の各成分の値を更新しています。先ほど説明したワーシャルフロイド法の手順で言うとSTEP 2~STEP nがこのコードに対応します。
kはステップ数を表しています。各ステップに対してD_nextという行列を用意します。これはのちに説明する計算によって得られた値を保持する行列で、初期値として全ての要素を0としています。
例えば今ステップ1(k=0)のとき、引数Dの\((i,j)\)成分は\(d_{ij}^{(0)}\)となりますが、この状態から
\(d_{ij}^{(1)} = \min\{d_{ij}^{(0)}, d_{i1}^{(0)} + d_{j1}^{(0)}\}\)
という計算式に従って\(d_{ij}^{(1)}\)を求めます。この\(d_{ij}^{(1)}\)を保持する行列がD_nextということになります。
※pythonのリストはインデックスが0から始まるのでステップ1がk=0となります。これ以降もインデックスが0から始まることに注意して見てみてください。
ステップ kにおいて\(d_{ij}^{(k)}\)を計算するための式は
\(d_{ij}^{(k)} = \min\{d_{ij}^{(k-1)}, d_{ik}^{(k-1)} + d_{jk}^{(k-1)}\}\)
です。この式を言い換えると、
\(d_{ij}^{(k-1)} > d_{ik}^{(k-1)} + d_{jk}^{(k-1)}\)だったら\(d_{ij}^{(k)} = d_{ik}^{(k-1)} + d_{jk}^{(k-1)}\)
\(d_{ij}^{(k-1)} \leq d_{ik}^{(k-1)} + d_{jk}^{(k-1)}\)だったら\(d_{ij}^{(k)} = d_{ij}^{(k-1)}\)
です。これをpythonで表すと以下のようになります。
# 行列の各成分の値を更新する
if D[i][j] > D[i][k] + D[k][j]:
D_next[i][j] = D[i][k] + D[k][j]
else:
D_next[i][j] = D[i][j]
これをfor i in range(n) for j in range(n)で1~nまで回しているって感じです。
D = D_nextで次のステップに移るための準備をしています。

例えばSTEP 1(k=0)でD_nextの各成分\(d_{ij}^{(1)}\)を全て計算することができたとします。STEP 2ではD_nextの各成分\(d_{ij}^{(1)}\)の値を使って\(d_{ij}^{(2)}\)を計算します。この計算手順はSTEP 1の時とほぼ同じなので下のコードを使い回したいです。
# 行列の各成分の値を更新する
if D[i][j] > D[i][k] + D[k][j]:
D_next[i][j] = D[i][k] + D[k][j]
else:
D_next[i][j] = D[i][j]それを達成するためにはSTEP 1で得られたD_nextをDとし、D_nextをまた新しく作ればOKです。そのためコードの最後にD = D_nextと書いています。
計算結果を返す
return D # (i,j)成分が頂点iから頂点jへの最短距離となる行列を返す
最後の行で計算結果を返しています。for k in range(n) for i in range(n) for j in range(n)でi,j,kを0からn-1まで回して計算することによって、\((i,j)\)成分が頂点\(i\)から頂点\(j\)への最短距離となる行列Dを得ることができました。
最後にこれを返す必要があるのでreturn DでDを返しています。
実際に計算してみる
inf = 10000000 # ∞を設定する
D = [[inf,1,-2,inf,inf],[inf,inf,inf,5,1],[4,3,inf,inf,4],[inf,inf,-4,inf,-2],[inf,inf,inf,3,inf]] # 重み付き隣接行列
print(floyd_warshall(D)) #結果を返す
上のコードで実際に計算してみました。pythonで∞を表現するためのテクニックとして、めちゃめちゃ大きい数字を使うという方法があります。今回はその方法を使います。infをめちゃめちゃ大きい数字としました。
入力値の重み付き隣接行列Dを上のように設定しました。この行列は下のグラフの重み付き隣接行列を表しています。


上記のコードを実行したら上のような結果が得られました。これを見ると例えば(2,1)成分が3なので頂点2から頂点1への最短距離が3であることが分かりました。
負閉路を持つグラフを入力してみる
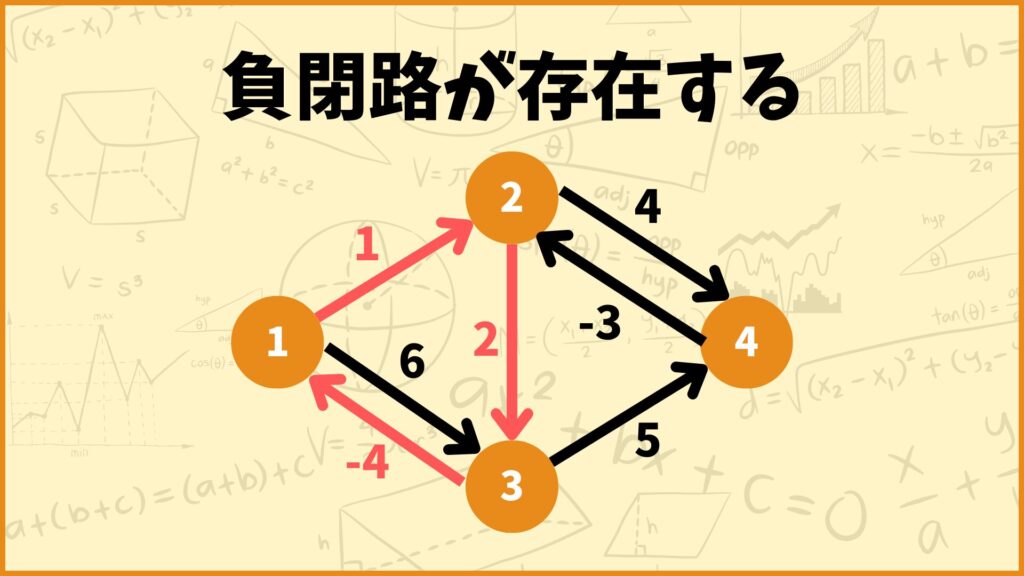
それでは最後に上のグラフの重み付き隣接行列を入力してみます。上のグラフは頂点1→頂点2→頂点3→頂点1の負閉路を持つグラフです。
inf = 10000000 # ∞を設定する
D = [[inf,1,6,inf],[inf,inf,2,4],[-4,inf,inf,5],[inf,-3,inf,inf]] # 重み付き隣接行列
print(floyd_warshall(D)) #結果を返す
負閉路の検知方法は
「得られた行列の対角成分に負の値があれば負閉路を持つ」
です。上の結果を見ると\((1,1),(2,2),(3,3)\)成分が負の値となっていますね。よってこのグラフは負閉路を持つグラフだということが検知できました。
おわりに
いかがでしたか。
今回の記事ではワーシャルフロイド法とpythonについて解説していきました。
今後もこのような組合せ最適化に関する記事を書いていきます!
最後までこの記事を読んでくれてありがとうございました。




