- 勾配法ってなに？
- 勾配法のアルゴリズムを知りたい…
- 勾配法をpythonで実装したい…
こんにちは！しゅんです！
今回は勾配法について解説していきます！またpythonでの実装方法についても解説します！
それではやっていきましょう！
普段は組合せ最適化の記事を書いてたりします。
ぜひ他の記事も読んでみてください！
このブログの簡単な紹介はこちらに書いてあります。
興味があったら見てみてください。
このブログでは経営工学を勉強している現役理系大学生が、経営工学に関することを色々話していきます！
ぼくが経営工学を勉強している中で感じたことや、興味深かったことを皆さんと共有出来たら良いなと思っています。
そもそも経営工学とは何なのでしょうか。Wikipediaによると
経営工学（けいえいこうがく、英: engineering management）は、人・材料・装置・情報・エネルギーを総合したシステムの設計・改善・確立に関する活動である。そのシステムから得られる結果を明示し、予測し、評価するために、工学的な分析・設計の原理・方法とともに、数学、物理および社会科学の専門知識と経験を利用する。
引用元 : 経営工学 – Wikipedia
長々と書いてありますが、要は経営、経済の課題を理系的な観点から解決する学問です。
勾配法ってなに？
勾配法は微分を使って関数の最小値、または最大値を求める方法です。もっと正確に言うと、関数の最小値に近い値、最大値に近い値を求める方法が勾配法です。
特に最小値（に近い値）を求める方法を勾配降下法、最大値（に近い値）を求める方法を勾配上昇法と言ったりします。
- 勾配降下法：最小値（に近い値）を求める方法
- 勾配上昇法：最大値（に近い値）を求める方法
この記事では関数の最小値を求めるために勾配法を使います。これ以降、勾配法と書かれたときは勾配降下法のことを指していると考えてください。
勾配法のアルゴリズムってなに？
簡単のためこの記事では1変数関数\(f(x)\)を使って勾配法のアルゴリズムを説明します。
勾配法のアルゴリズム
STEP 0：
初期点 \(x_0\) と学習率 \(\eta\) と反復回数 \(k\) を設定する。
STEP 1：
\(f'(x_0)\)を求め
\(x_1=x_0-\eta f'(x_0)\)
とする。
STEP 2：
\(f'(x_1)\)を求め
\(x_2=x_1-\eta f'(x_1)\)
とする。
・
・
・
STEP \(k\)：
\(f'(x_{k-1})\)を求め
\(x_k=x_{k-1}-\eta f'(x_{k-1})\)
とし、\(x_k\)を返す。
上記が勾配法のアルゴリズムです。数式を見せられても何をしてるかよく分からないので、具体例を使って勾配法のアルゴリズムを見ていきましょう。
具体例を使って勾配法で関数の最小値を求めてみる
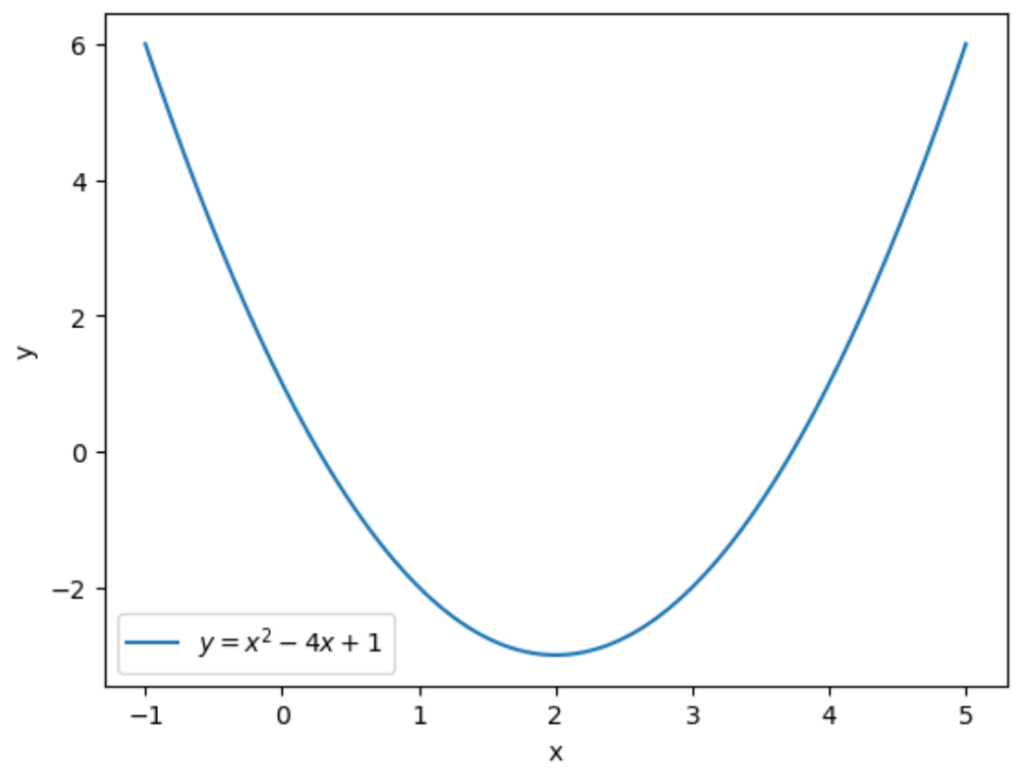
ということで上の関数を例にして、勾配法によってこの関数の最小値を求めたいと思います。上の関数は\(f(x)=x^2-4x+1\)で、\(x=2\)のとき最小値\(-3\)を取ります。
STEP 0
STEP 0：
初期点 \(x_0\) と学習率 \(\eta\) と反復回数 \(k\) を設定する。
STEP 0では初期点 \(x_0\) と学習率 \(\eta\) と反復回数 \(k\) を設定します。今回は
初期点：\(x_0=4\)
学習率：\(\eta=0.2\)
反復回数：\(k=7\)
とします。
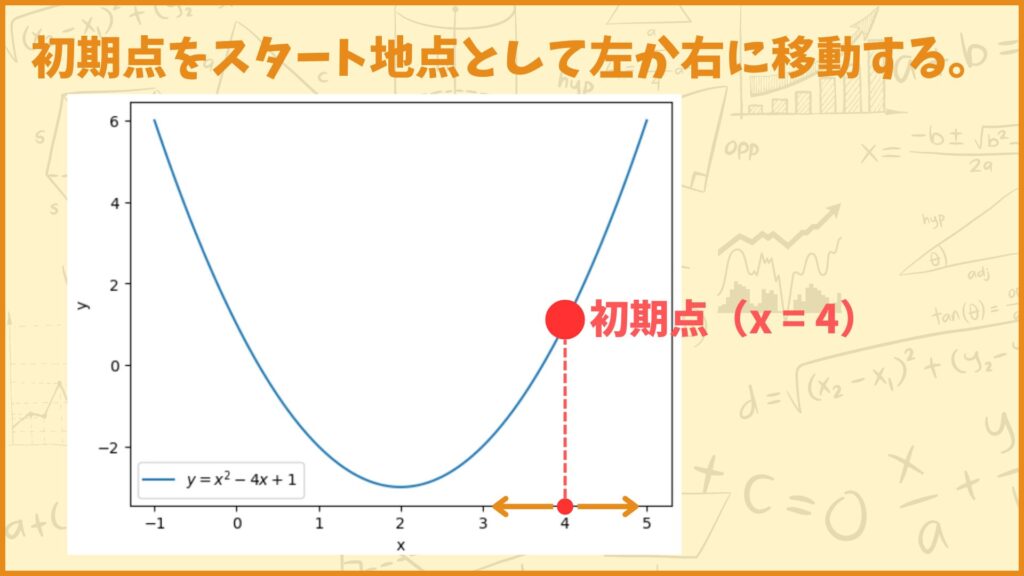
初期点とは最小値を求めるために最初に出発する点です。
初期点をスタート地点として、最小値となる点にどんどん移動していくのが勾配法です。初期点はどこに設定しても良いのですが、今回は\(x_0=4\)を初期点としました。
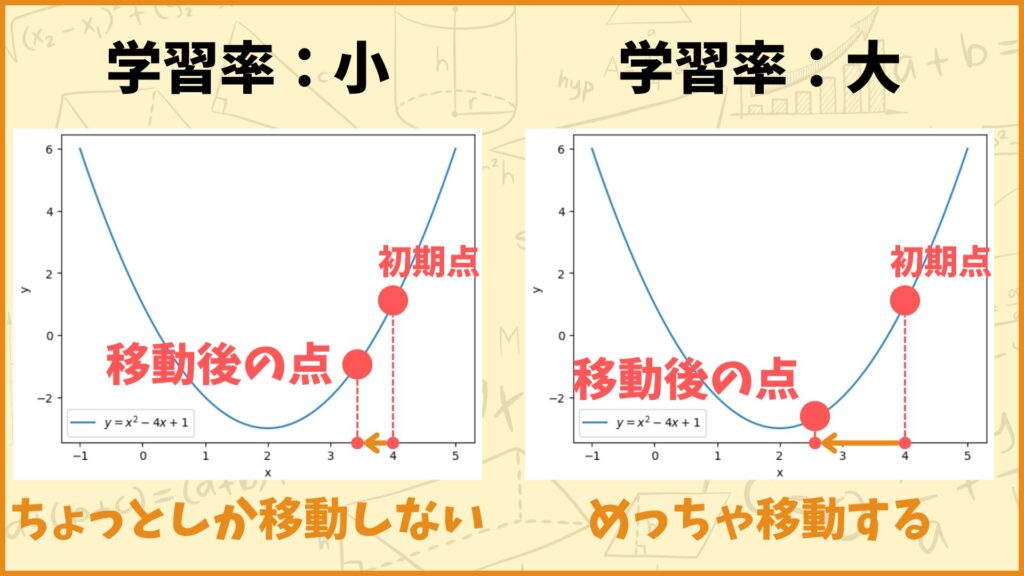
学習率は今の点からどれだけ移動するかを決定するパラメータです。例えば上図のように、初期点から左に移動した方が最小値に近づくとします。
このとき学習率を小さく設定したら初期点からちょっとしか移動しませんが、学習率を大きく設定したら初期点からめっちゃ移動します。
学習率をどれくらいの大きさにするかは難しい問題で、大きすぎてもダメだし、小さすぎてもダメなんです。詳しい話は第5章で行います。
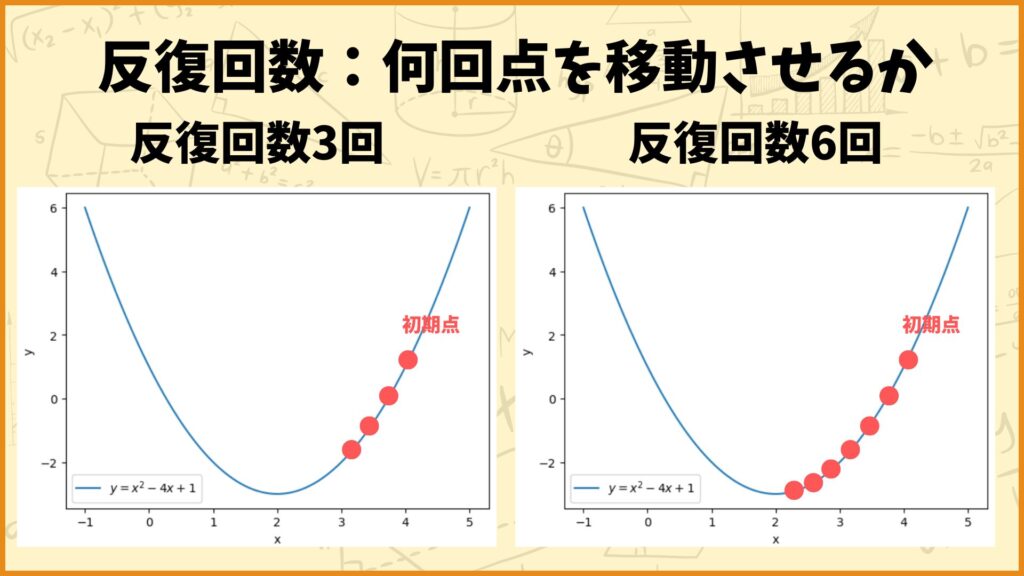
反復回数は、初期点から何回点を移動させるかを表します。上図の左側は反復回数が3回の例を表しており、右側は反復回数が6回の例を表しています。
反復回数を大きくすれば最小解に近づく可能性が高くなります。その一方で反復回数を大きくすればその分計算時間も長くなります。
STEP 1
STEP 1：
\(f'(x_0)\)を求め
\(x_1=x_0-\eta f'(x_0)\)
とする。
\(f(x)=x^2-4x+1\) なので
\(f'(x)=2x-4\)
となります。\(x_0=4\) なので
\(f'(x_0)=f'(4)=2\times4-4=4\)
となります。\(x_0=4, \; \eta=0.2, \; f'(x_0)=4\) なので
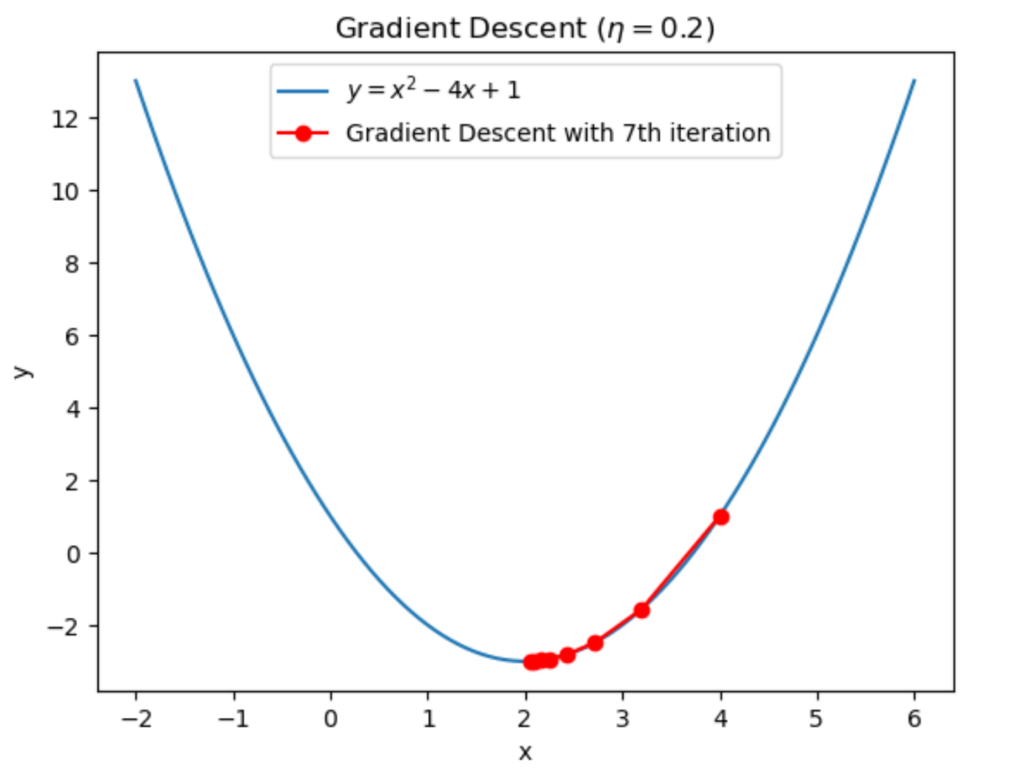
\(x_1=x_0-\eta f'(x_0)=4-0.2\times4=3.2\)
と計算できます。従って1回目の反復によって \(4\to3.2\) に更新されました。
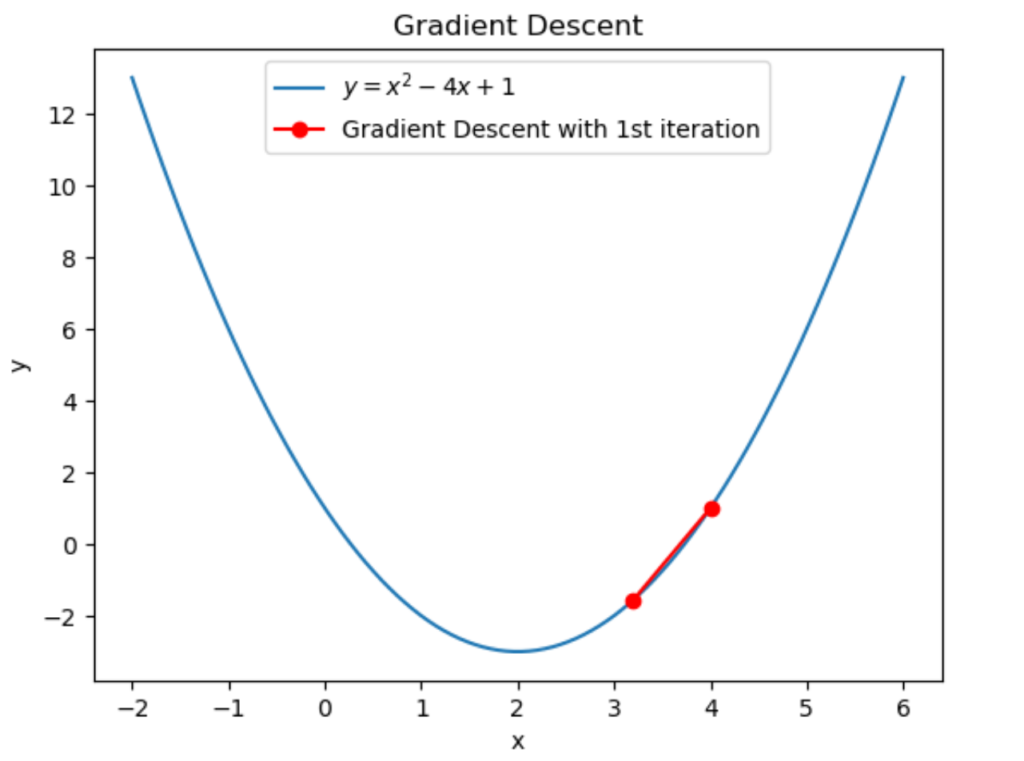
グラフにすると上図のようになります。ちゃんと最小解に近づいていますね。
なぜ \(x_1=x_0-\eta f'(x_0)\) によって最小解に近づいたのかを考えてみましょう。今回は \(x_0=4\) で \(f'(x_0)=4\) でした。これは「\(x=4\) のときの関数の傾きが4だった」ということを表していますが、見方を変えると「点 \(x=4\) より \(x\) を大きくすると関数が取る値は大きくなり、\(x\) を小さくすると関数が取る値は小さくなる可能性が高い」ということを表しています。
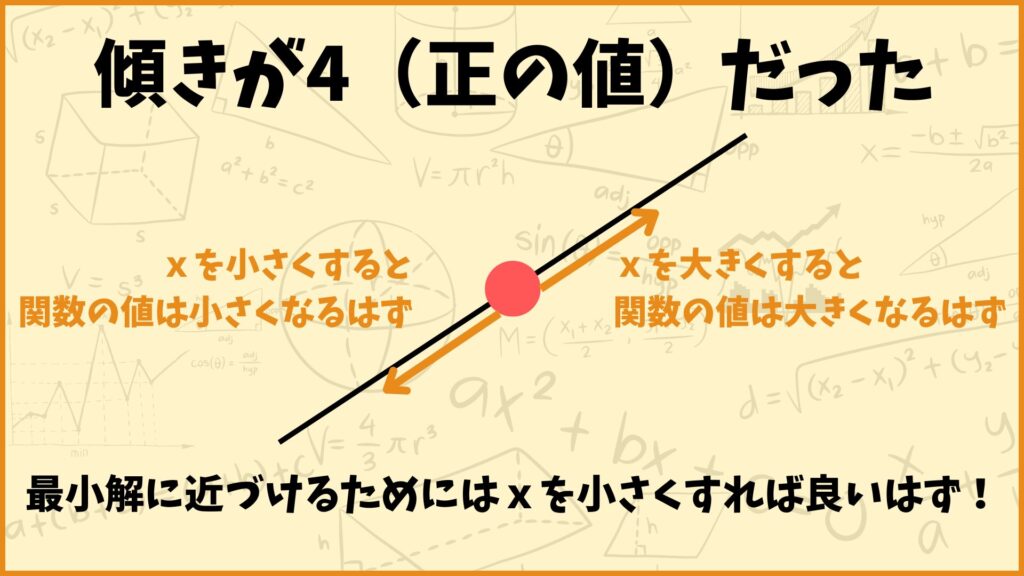
したがって最小解に近づけるためには \(x\) の値を小さくすれば良いと考えられます。今学習率 \(\eta\) は正の数で符号に影響は与えないことを考慮すると
\(x_1=x_0-\eta f'(x_0)\)
としたときに、\(\eta>0, \; f'(x_0)>0\) より \(x_1<x_0\) となり \(x\) の値を小さくすることができます。従って最小解に近づくことができます。
またこの式を見ると学習率 \(\eta\) は「どれだけ点を移動させるか」を決めるパラメータであることも分かります。\(\eta=0.2\) としたら \(x_1=4-0.2\times4=3.2\) となりましたが、もし \(\eta=0.002\) としたら \(x_1=4-0.002\times4=3.992\) となりほとんど移動していないことが分かります。
STEP 2
STEP 2：
\(f'(x_1)\)を求め
\(x_2=x_1-\eta f'(x_1)\)
とする。
\(f(x)=x^2-4x+1\) なので
\(f'(x)=2x-4\)
となります。\(x_1=3.2\) なので
\(f'(x_1)=f'(3.2)=2\times3.2-4=2.4\)
となります。\(x_1=3.2, \; \eta=0.2, \; f'(x_1)=2.4\) なので
\(x_2=x_1-\eta f'(x_1)=3.2-0.2\times2.4=2.72\)
と計算できます。従って2回目の反復によって \(3.2\to2.72\) に更新されました。
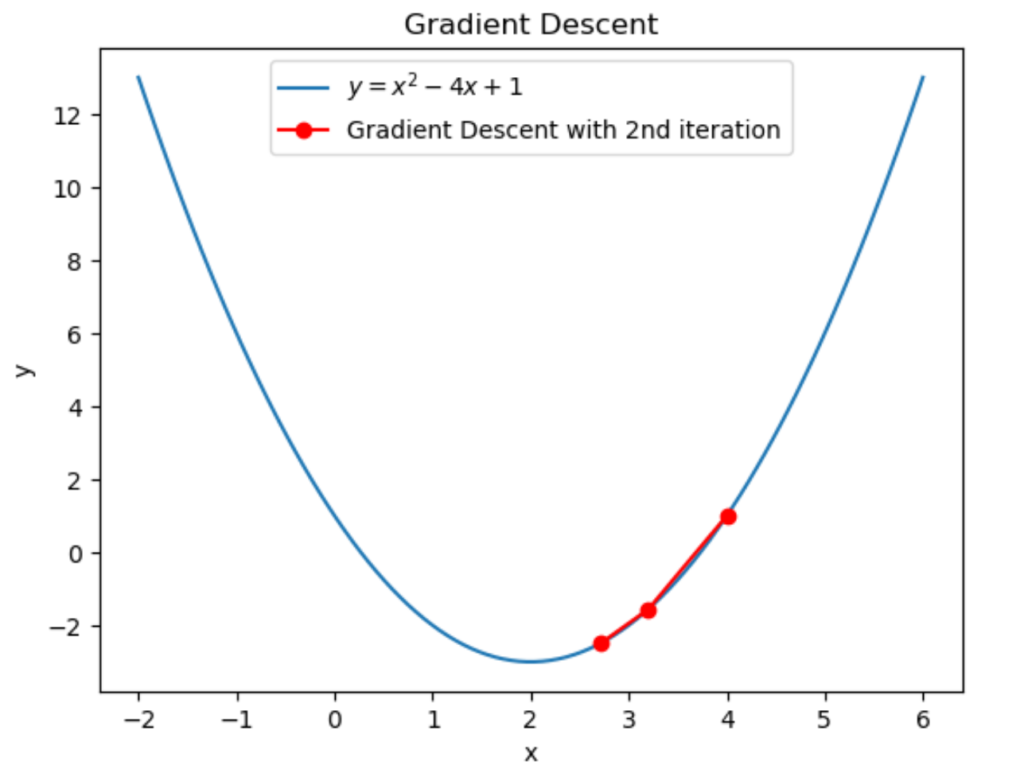
グラフにすると上図のようになります。ちゃんと最小解に近づいていますね。
STEP 3
STEP 3：
\(f'(x_2)\)を求め
\(x_3=x_2-\eta f'(x_2)\)
とする。
\(f(x)=x^2-4x+1\) なので
\(f'(x)=2x-4\)
となります。\(x_2=2.72\) なので
\(f'(x_2)=f'(2.72)=2\times2.72-4=1.44\)
となります。\(x_2=2.72, \; \eta=0.2, \; f'(x_2)=1.44\) なので
\(x_3=x_2-\eta f'(x_2)=2.72-0.2\times1.44=2.432\)
と計算できます。従って3回目の反復によって \(2.72\to2.432\) に更新されました。
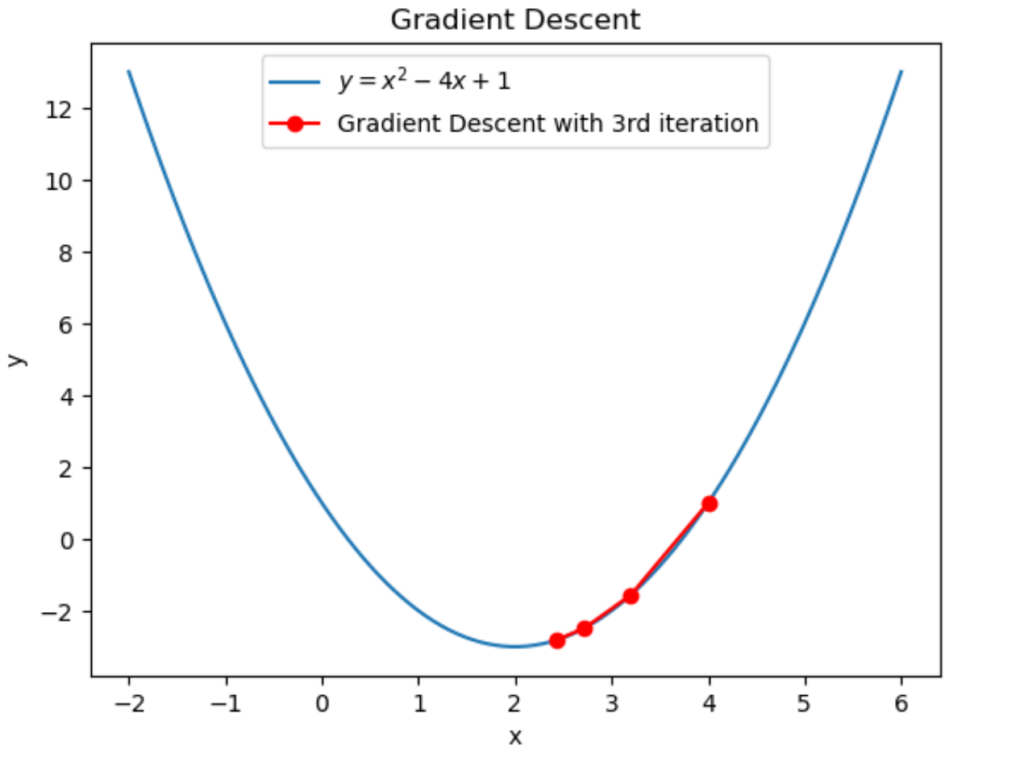
グラフにすると上図のようになります。ちゃんと最小解に近づいていますね。
STEP 4
STEP 4：
\(f'(x_3)\)を求め
\(x_4=x_3-\eta f'(x_3)\)
とする。
\(f(x)=x^2-4x+1\) なので
\(f'(x)=2x-4\)
となります。\(x_3=2.432\) なので
\(f'(x_3)=f'(2.432)=2\times2.432-4=0.864\)
となります。\(x_3=2.432, \; \eta=0.2, \; f'(x_3)=0.864\) なので
\(x_4=x_3-\eta f'(x_3)=2.432-0.2\times0.864=2.2592\)
と計算できます。従って4回目の反復によって \(2.432\to2.2592\) に更新されました。
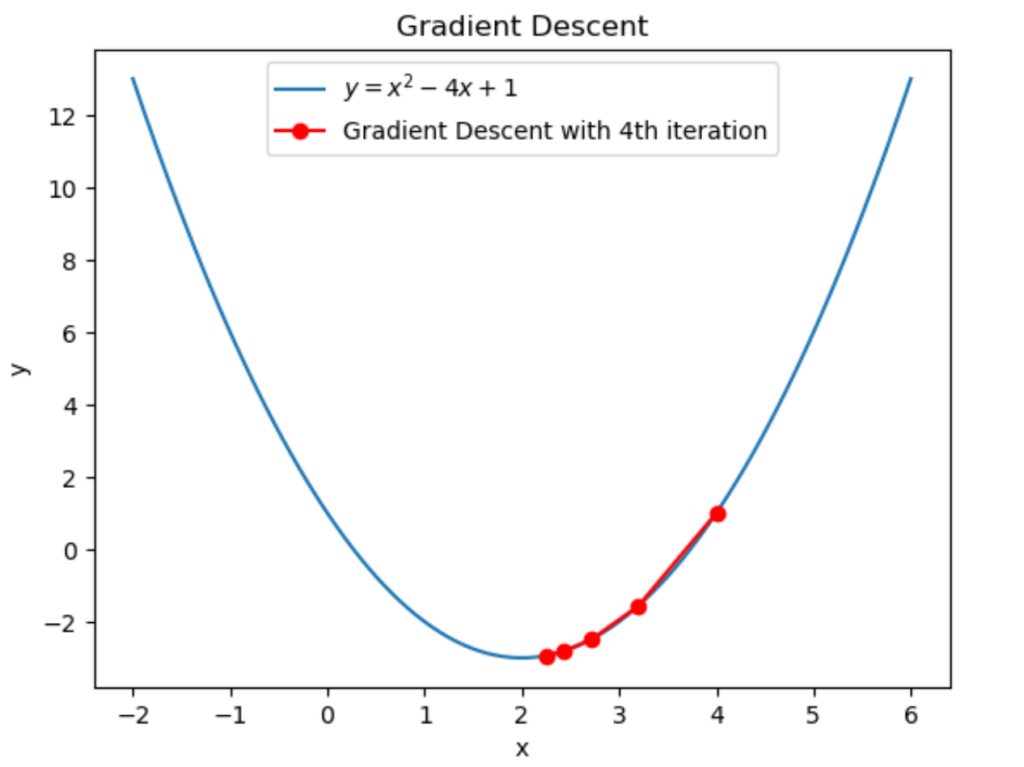
グラフにすると上図のようになります。ちゃんと最小解に近づいていますね。
STEP 5
STEP 5：
\(f'(x_4)\)を求め
\(x_5=x_4-\eta f'(x_4)\)
とする。
\(f(x)=x^2-4x+1\) なので
\(f'(x)=2x-4\)
となります。\(x_4=2.2592\) なので
\(f'(x_4)=f'(2.2592)=2\times2.2592-4=0.5184\)
となります。\(x_4=2.2592, \; \eta=0.2, \; f'(x_4)=0.4184\) なので
\(x_5=x_4-\eta f'(x_4)=2.2592-0.2\times0.4184=2.15552\)
と計算できます。従って5回目の反復によって \(2.2592\to2.15552\) に更新されました。
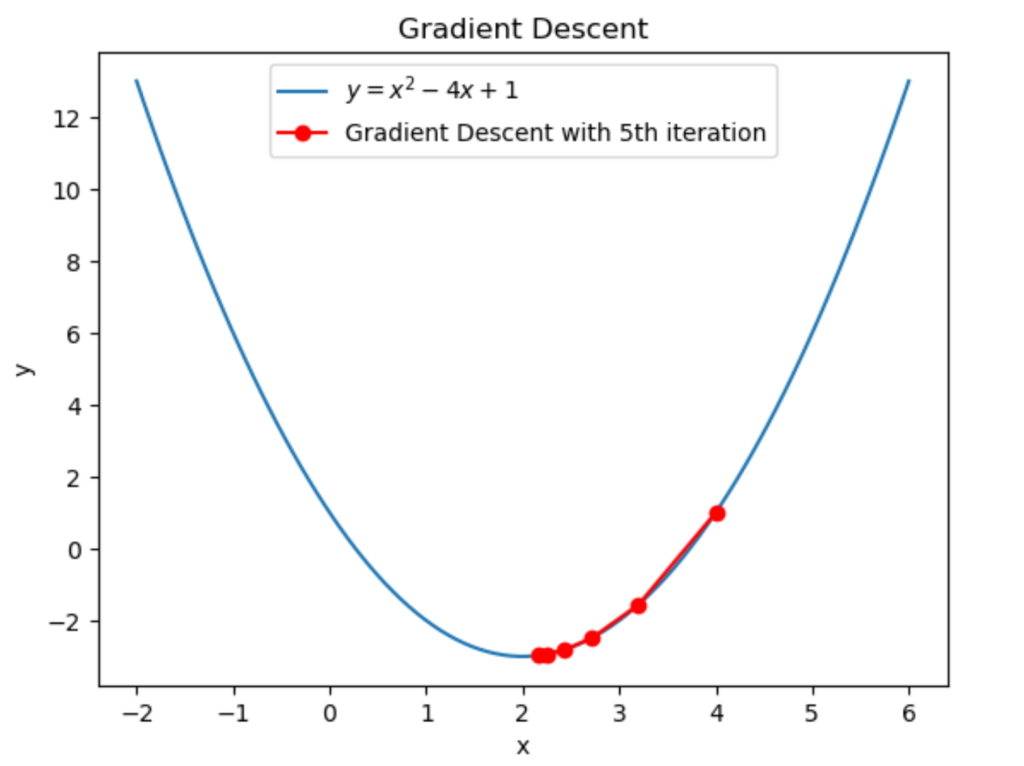
グラフにすると上図のようになります。ちゃんと最小解に近づいていますね。
STEP 6
STEP 6：
\(f'(x_5)\)を求め
\(x_6=x_5-\eta f'(x_5)\)
とする。
\(f(x)=x^2-4x+1\) なので
\(f'(x)=2x-4\)
となります。\(x_5=2.15552\) なので
\(f'(x_5)=f'(2.15552)=2\times2.15552-4=0.31104\)
となります。\(x_5=2.15552, \; \eta=0.2, \; f'(x_5)=0.31104\) なので
\(x_6=x_5-\eta f'(x_5)=2.15552-0.2\times0.31104=2.093312\)
と計算できます。従って6回目の反復によって \(2.15552\to2.093312\) に更新されました。
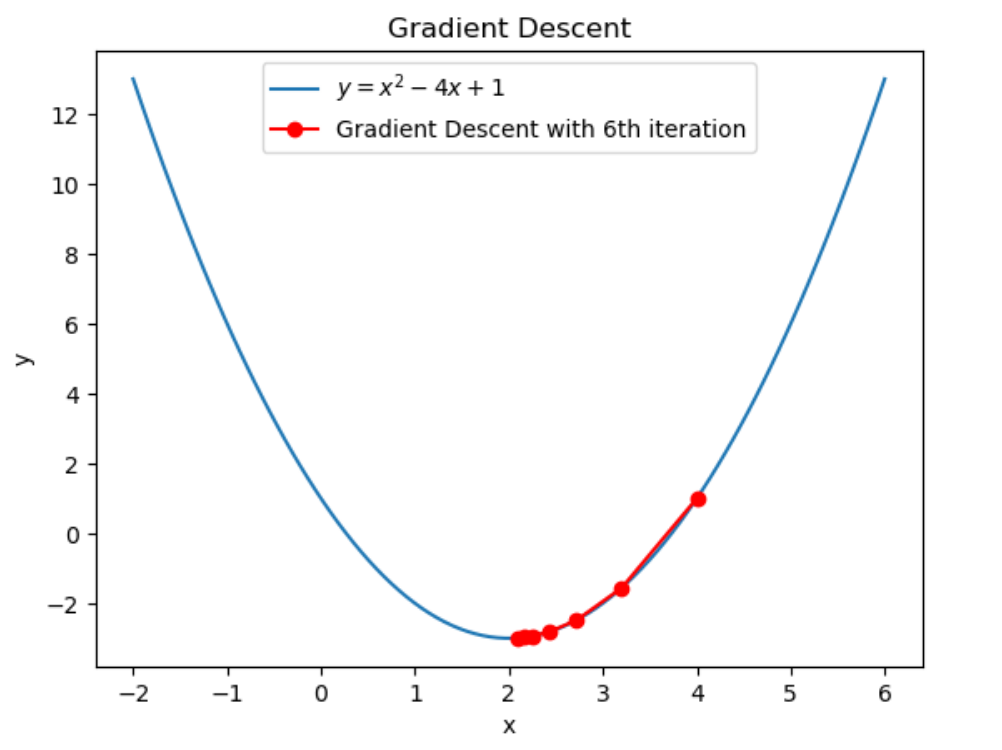
グラフにすると上図のようになります。ちゃんと最小解に近づいていますね。
STEP 7
STEP 7：
\(f'(x_6)\)を求め
\(x_7=x_6-\eta f'(x_6)\)
とする。
\(f(x)=x^2-4x+1\) なので
\(f'(x)=2x-4\)
となります。\(x_6=2.093312\) なので
\(f'(x_6)=f'(2.093312)=2\times2.093312-4=0.186624\)
となります。\(x_6=2.093312, \; \eta=0.2, \; f'(x_6)=2.093312\) なので
\(x_7=x_6-\eta f'(x_6)=2.093312-0.2\times0.186624=2.0559872\)
と計算できます。従って7回目の反復によって \(2.093312\to2.0559872\) に更新されました。
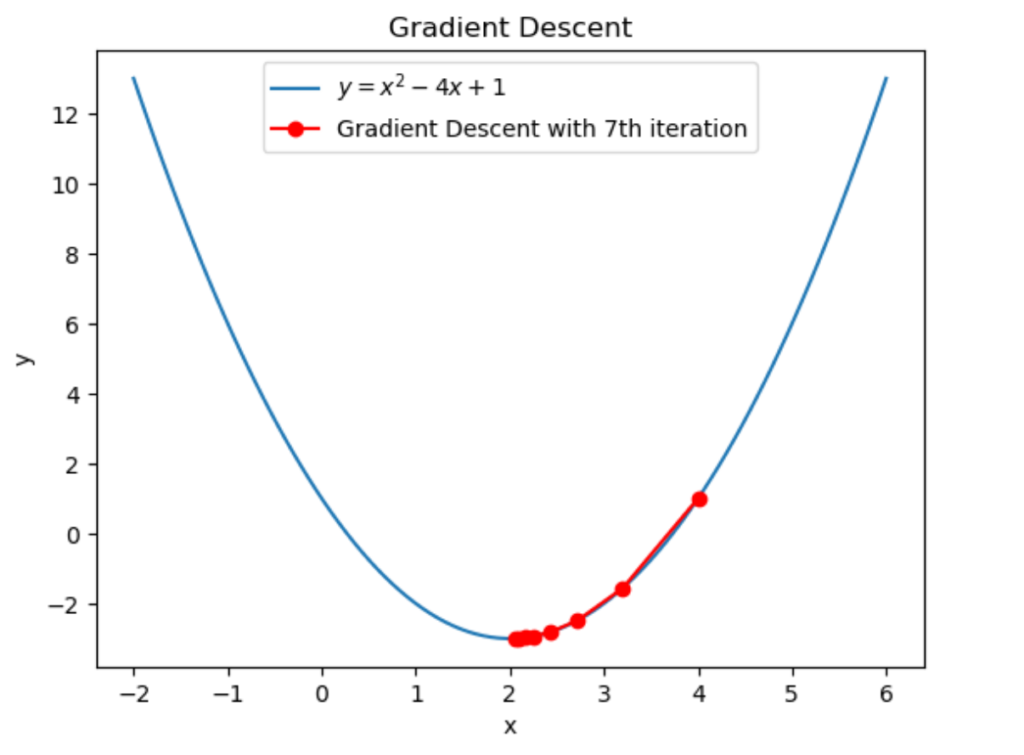
グラフにすると上図のようになります。ちゃんと最小解に近づいていますね。
反復回数を7回としたので \(x\) の更新を止めます。最後に \(x=2.0559872\) を出力して勾配法を終了します。
結果を確認する
勾配法によって \(x=2.0559872\) が得られました。最小解 \(x=2\) ではありませんが、かなり近い値となっています。
今回は反復を7回で止めましたが、もっと反復回数を増やせば
反復回数8回：\(x=2.03359232\)
反復回数9回：\(x=2.020155392\)
反復回数10回：\(x=2.0120932352\)
反復回数11回：\(x=2.00725594112\)
反復回数12回：\(x=2.004353564672\)
反復回数13回：\(x=2.0026121388032\)
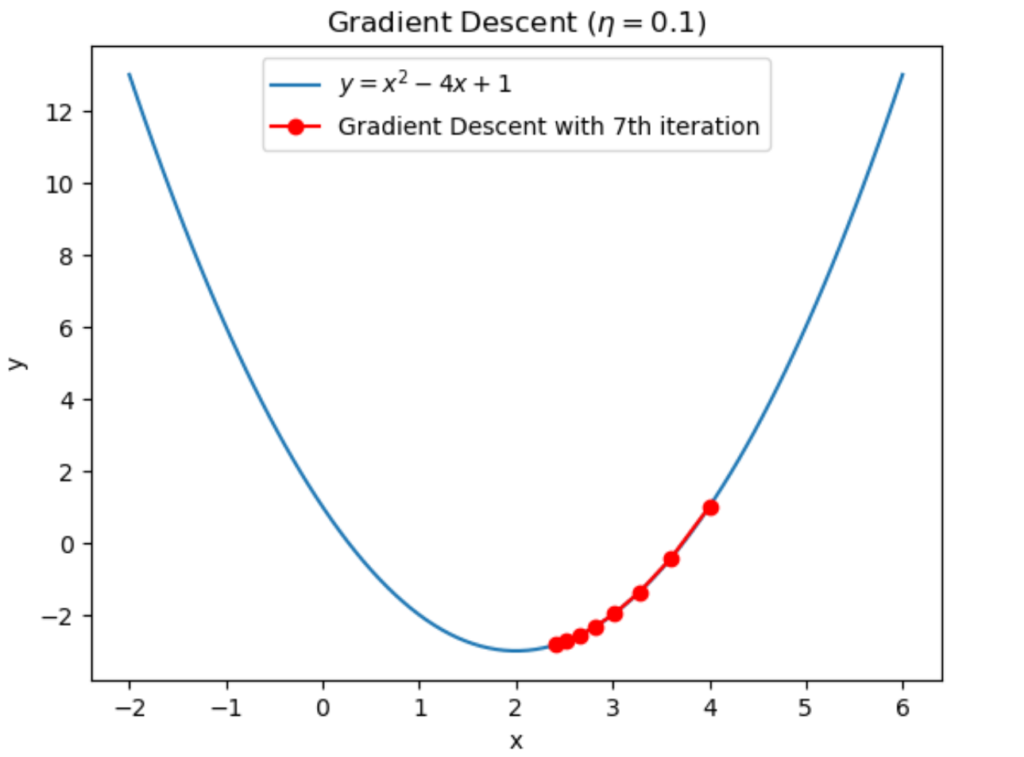
とどんどん \(x=2\) に近づいていくのが分かります。また学習率 \(\eta\) の値を \(\eta=0.1\) とすると
反復回数1回：\(x=3.6\)
反復回数2回：\(x=3.28\)
反復回数3回：\(x=3.024\)
反復回数4回：\(x=2.8192\)
反復回数5回：\(x=2.65536\)
反復回数6回：\(x=2.524288\)
反復回数7回：\(x=2.4194304\)
となり、\(\eta=0.2\) の時に比べて最小解 \(x=2\) へ移動するスピードが遅くなっているのが分かります。
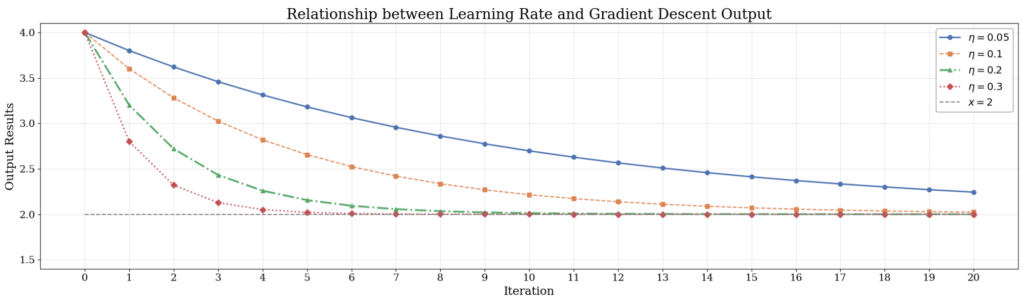
学習率を \(\eta=0.05,0.1,0.2,0.3\) と変化させたときに、各反復で返される \(x\) の値をグラフにしてみました。
これを見ると学習率を大きくすれば早く最小解に収束し、小さくすれば収束するスピードが遅くなっているのが分かります。
学習率は大きすぎても小さすぎてもダメ
第4章の例を使って学習率が大きすぎても小さすぎてもダメなことを確認してみましょう。
学習率が大きいと大きな値に発散する
学習率を \(\eta=0.0000001\) にして第4章で使った関数 \(f(x)=x^2-4x+1\) に勾配法を適用してみます。学習率以外のパラメータは第4章と同じにします。
初期点：\(x_0=4\)
学習率：\(\eta=0.0000001\)
反復回数：\(k=7\)
反復回数0回：\(x=4\)
反復回数1回：\(x=3.9999996\)
反復回数2回：\(x=3.9999992000000804\)
反復回数3回：\(x=3.9999988000002404\)
反復回数4回：\(x=3.9999984000004805\)
反復回数5回：\(x=3.9999980000008004\)
反復回数6回：\(x=3.9999976000012003\)
反復回数7回：\(x=3.99999720000168\)
となり初期点の \(x=4\) からほとんど動いていないことが分かります。
学習率が小さいと学習が進まない
学習率を \(\eta=10\) にして第4章で使った関数 \(f(x)=x^2-4x+1\) に勾配法を適用してみます。学習率以外のパラメータは第4章と同じにします。
初期点：\(x_0=4\)
学習率：\(\eta=10\)
反復回数：\(k=7\)
反復回数0回：\(x=4\)
反復回数1回：\(x=-36\)
反復回数2回：\(x=724\)
反復回数3回：\(x=-13716\)
反復回数4回：\(x=260644\)
反復回数5回：\(x=-4952196\)
反復回数6回：\(x=94091764\)
反復回数7回：\(x=-1787743476\)
となり非常に大きな値を返します。最小解 \(x=2\) からどんどん遠ざかっています。
pythonで勾配法を実装する
それでは次に勾配法をpythonで実装してみましょう。例として第4章で行った勾配法を実装したいと思います。
## 勾配法の実装
def gradient_descent(learning_rate, initial_x, iterations):
x = initial_x # xの初期値を設定
x_history = [x] # 各反復でのxを記録するリストを設定
for i in range(iterations):
gradient = derivative_function(x) # 微分係数を計算
x = x - learning_rate * gradient # xを更新
x_history.append(x) # 記録リストにxを追加
return x_history
## 目的関数の定義
def objective_function(x):
return x**2 - 4*x + 1
## 目的関数の微分の定義
def derivative_function(x):
return 2*x - 4
## 学習率、初期値、反復回数を設定
learning_rate = 0.2
initial_x = 4
iterations = 7
## 勾配法を実行
x_history = gradient_descent(learning_rate, initial_x, iterations) # 結果を取得
print(x_history) # 結果を表示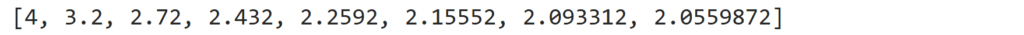
結論上のコードで勾配法を実行できます。このコードを実行したら上記の結果が得られました。それでは1つずつ解説していきましょう。
コードの解説
勾配法の実装
## 勾配法の実装
def gradient_descent(learning_rate, initial_x, iterations):
x = initial_x # xの初期値を設定
x_history = [x] # 各反復でのxを記録するリストを設定
for i in range(iterations):
gradient = derivative_function(x) # 微分係数を計算（derivative_function関数は後で定義する）
x = x - learning_rate * gradient # xを更新
x_history.append(x) # 記録リストにxを追加
return x_history
この部分では勾配法を実装しています。今回は関数として実装しました。関数名は「gradient_descent」、引数は「learning_rate」、「initial_x」、「iterations」の3つです。それぞれ学習率、初期点、反復回数を表します。
3行目では \(x\) の初期値を設定しています。
4行目では各反復で得られる \(x\) を記録するリストを設定しています。
6行目ではfor文を使って各反復を表現しています。
7行目で微分係数（勾配）を計算しています。この計算にはderivative_function関数を使っていますが、これは後で定義します。
8行目で\(x\)を更新しています。
9行目では記録リストに更新した後の\(x\)を追加しています。
目的関数とその微分の定義
## 目的関数の定義
def objective_function(x):
return x**2 - 4*x + 1
## 目的関数の微分の定義
def derivative_function(x):
return 2*x - 4
ここでは勾配法によって最小値を求めたい目的関数とその微分の定義をしています。目的関数は
\(f(x)=x^2-4x+1\)
で、目的関数を微分したときに得られる関数は
\(f'(x)=2x-4\)
です。目的関数は「objective_function」で定義して、目的関数を微分したときに得られる関数は「derivative_function」で定義しています。
各パラメータの定義
## 学習率、初期値、反復回数を設定
learning_rate = 0.2
initial_x = 4
iterations = 7
ここでは学習率、初期値、反復回数をそれぞれ設定しています。学習率は0.2、初期値は\(x=4\)、反復回数は7回としています。
各パラメータの定義
## 勾配法を実行
x_history = gradient_descent(learning_rate, initial_x, iterations) # 結果を取得
print(x_history) # 結果を表示
この部分では今設定したパラメータを使って勾配法を実行しています。「gradient_descent」関数によって得られた「x_history」は各反復での\(x\)を記録しているリストです。
結果を見る
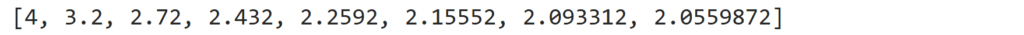
コードを実行したら上の結果が得られました。第4章で計算した得られた値と同じになっています。ちゃんと実装できていそうですね。
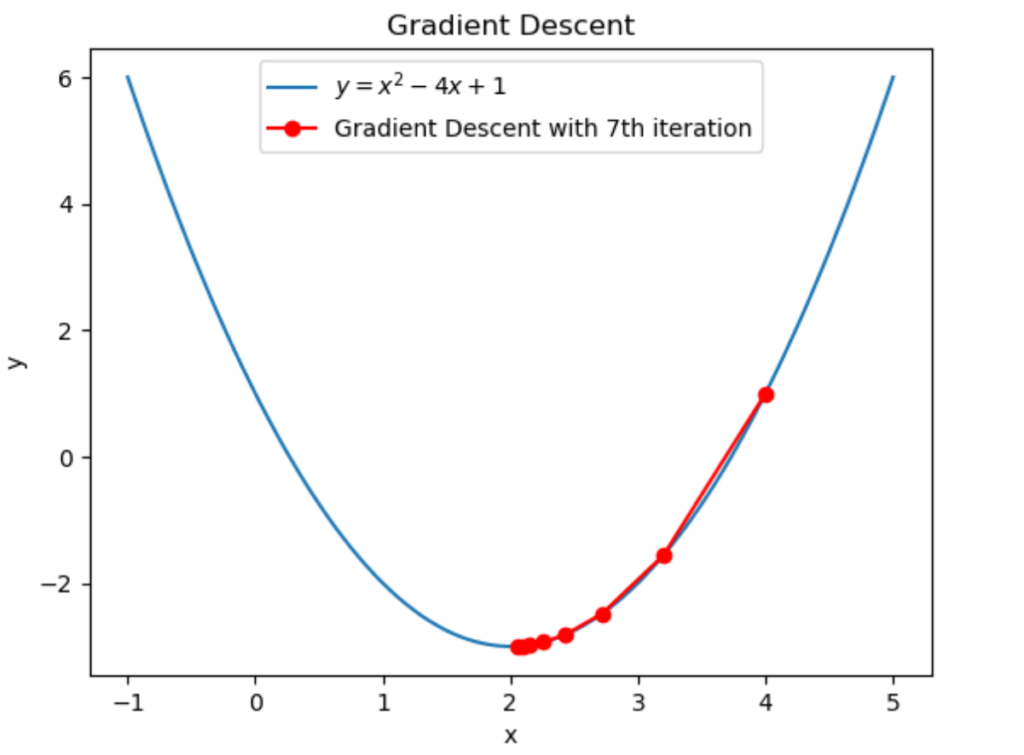
# グラフの描画
x_values = np.linspace(-1, 5, 100)
plt.plot(x_values, objective_function(x_values), label=r"$y = x^2 - 4x + 1$")
plt.plot(x_history, objective_function(np.array(x_history)), 'ro-', label="Gradient Descent with 7th iteration")
plt.xlabel("x")
plt.ylabel("y")
plt.legend()
plt.title("Gradient Descent")
plt.show()
勾配法の結果をグラフにしてみました。これも第4章で見てきたものと同じなので詳しい説明は省略します。
おわりに
いかがでしたか。
今回の記事では勾配法について解説しました。
今後もこのようなAI・機械学習に関する記事を書いていきます！
最後までこの記事を読んでくれてありがとうございました。
参考文献
