線形回帰をしてみよう！～pythonでデータ分析をしてみよう～【経営工学を専門にしている大学生の日記】

こんにちは！しゅんです！

線形回帰はデータ間の関係を明らかにするための1つの手法です。ぼくが統計の勉強をしていたときにでてきたので皆さんにもシェアしたいと思います！また今回は説明と一緒にpythonを使ってどんなものか確かめたいと思います。

それでは解説していきましょう！

回帰をザックリ説明すると与えられた情報から知りたい情報を求めることです。以下の例を見てみましょう。

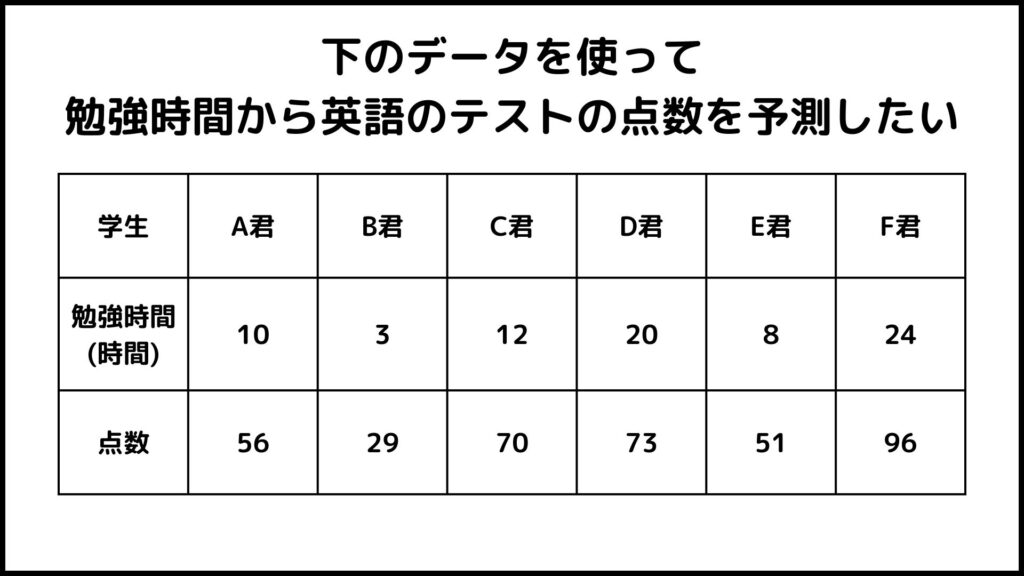
これはとある学校の学生の勉強時間とテストの点数データを集めたものです。このデータを使って勉強時間からテストの点数を予測することを考えます。

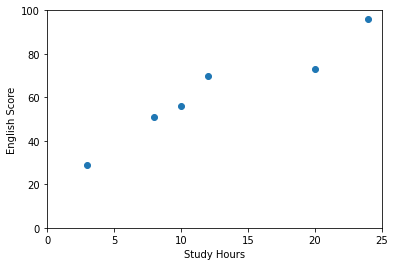
二つのデータの関係を見るのには散布図が便利です。

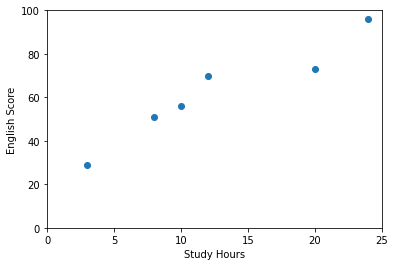
横軸が勉強時間で縦軸がテストの点数です。これを見ると勉強時間とテストの点数の間には正の相関関係がありそうですね。

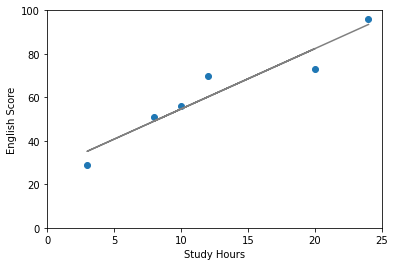
回帰はこの関係を式で表して予測することです。例えば今回の例で言うとだいたい下のような直線が引けそうですね。

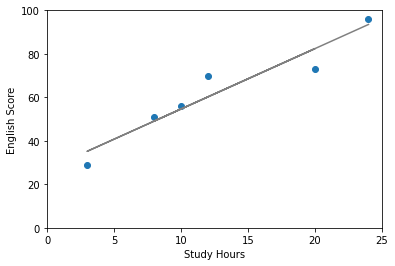
このグレーの直線は

で表されます。もしこの式が分かれば、勉強時間からテストの点数が予測できます。
例えば勉強時間が15時間の生徒がテストで何点取れるのかを予測したい場合は

となります。つまりだいたい69点くらい取れるということが予測できました。
以上のように回帰分析をすることで与えられている情報から知りたい情報を予測することが出来ます。

回帰には様々な種類が存在します。その中でも今回は線形回帰と非線形回帰、そして単回帰と重回帰について解説したいと思います。

線形回帰

線形回帰は線形の性質を持つと仮定して行う回帰です。

という声が出てくると思います。

ざっくり言うと線形とは直線のことです。例えば先ほど紹介した例はだいたい直線で表すことができていますよね。このように直線で表すための回帰が線形回帰です。

非線形回帰

直線で表せそうな場合は線形回帰を行うと説明しました。
ところが下の図のような場合ではどうでしょうか。

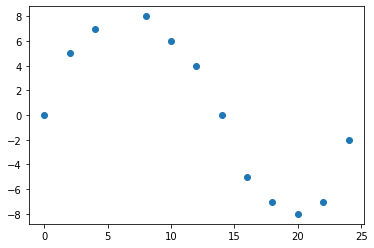
このデータを直線で表すことはちょっと難しいですよね。このように直線で表すことができそうにない場合は線形回帰は使えません。線形じゃないことを非線形と言い、非線形の性質を持つときには非線形回帰を行います。

単回帰

単回帰は説明変数が1つのときに行う回帰です。回帰の説明をしたときに用いた例では、「勉強時間」という説明変数1つのみで目的変数である「点数」を説明しているので単回帰です。

重回帰

重回帰は説明変数が2つ以上の場合に行う回帰です。以下の例を見てみましょう。

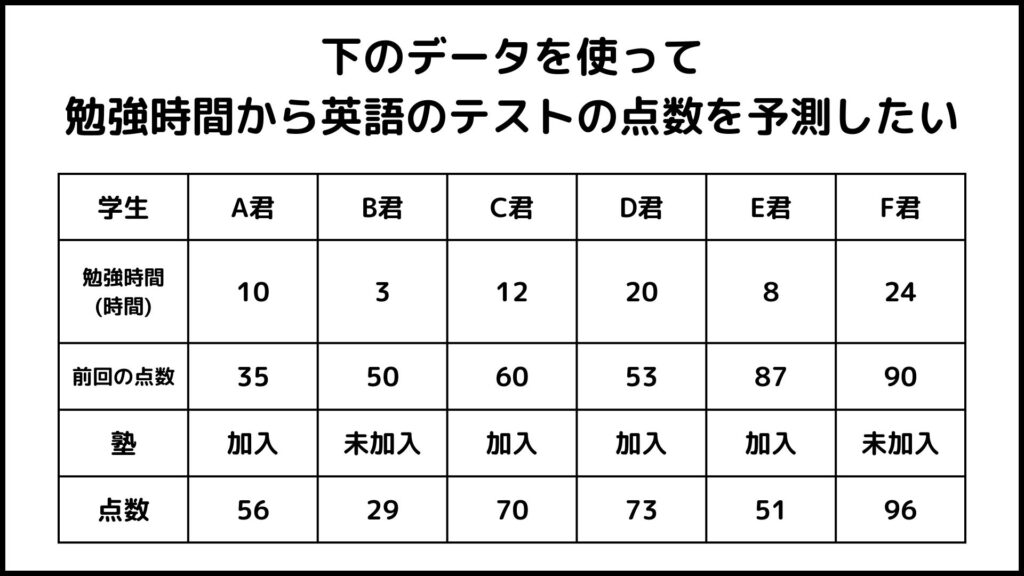
「勉強時間」に加えて「前回の点数」、「塾への加入・未加入」というデータを使って点数の予測をすることを考えます。この場合説明変数は「勉強時間」、「前回の点数」、「塾への加入・未加入」の3つになります。

このように2つ以上の説明変数を用いて目的変数の予測をしたい場合は重回帰を行います。

ということで今回は線形単回帰をpythonで実行してみたいと思います。

目標は下のグラフを表示することです。

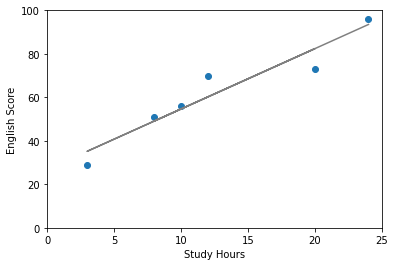
今回はnumpyとmatplotlibを使ってやってみたいと思います。numpyは数値計算を楽にしてくれるやつで、maatplotlibはグラフを作成するのに使えるやつです。

#numpyをnpとしてインポートする
import numpy as np
#matplotlibをpltとしてインポートする
import matplotlib.pyplot as plt 

この先numpyとmatplotlibをたくさん使っていきますが、いちいちnumpy、matplotlibって書いてたらめんどくさいです。ということで基本的にnp、pltと省略して使うことにします。

それではまずnumpyを使って今回使うデータを作成してみましょう。

#勉強時間のデータを作成
hour = np.array([10,3,12,20,8,24]).reshape(-1,1)
#テストの点数のデータを作成
score = np.array([56,29,70,73,51,96])

np.array()はnumpyで配列を作成するときに使うやつです。例えばscoreを表示すると以下のようになります。

scoreにはこんな形にデータが格納されます。またhourの後ろについている.reshape(-1,1)は線形回帰をするために適した配列に変形しています。これも表示してみましょう。

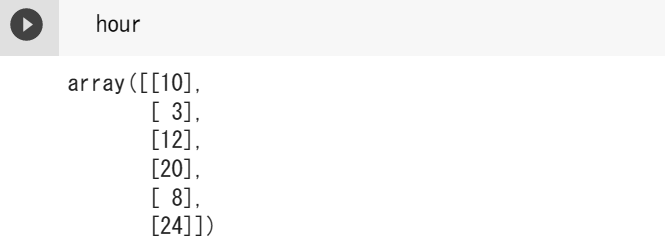
scoreとは配列の形が違いますよね。実は説明変数を普通にnp.arrayで作成しても線形回帰を実行するときにエラーが出てしまいます。気を付けてください。

まずは散布図を作成する

それではこのデータを使ってまずは散布図を作成してみましょう。ここではmatplotlibを使いたいと思います。先ほどmatplotlibをpltと定義したので、基本的にはplt.~で指示が出せます。

# 横軸hour, 縦軸scoreの散布図を作成
plt.scatter(hour,score)
# 横軸のラベルをとしてStudy Hoursを表示
plt.xlabel("Study Hours")
# 縦軸のラベルをとしてEnglish Scoreを表示
plt.ylabel("English Score")
# 表示するx座標の範囲を指定（0～25までを表示）
plt.xlim(0,25)
# 表示するy座標の範囲を指定 (0～100までを表示)
plt.ylim(0,100)

ということで散布図を作成することができました。

散布図を作成するにはplt.scatter(横軸のデータ, 縦軸のデータ)でできます。これだけでも散布図は作成できますが、見栄えをよくするために色々付け加えることができます。

例えばplt.xlabel(“名前”)とすれば横軸に名前を付けることができます。

線形回帰を実行する

それではいよいよ線形回帰をやってみましょう。線形回帰はscikit-learnというものを使ってやります。scikit-learnとは機械学習やデータ分析に関する色々な手法が使える超便利なライブラリです。データ分析をするときにはよく使うので覚えておきましょう。

それではscikitlearnから線形回帰をするためのやつをインポートしましょう。

# scikit-leranから線形回帰をするためのやつをインポートする
from sklearn.linear_model import LinearRegression

これのおかげで本来は結構大変な計算をしなきゃいけない線形回帰がすぐにできます。
それでは線形回帰をしてみましょう。

reg = LinearRegression()
reg.fit(hour, score)

hourを説明変数、scoreを目的変数として線形回帰をしたデータにregという名前を付けました。regの中身を見ていきましょう。

# 直線の傾き（回帰係数）を表示
print(reg.coef_)
# 直線の切片を表示
print(reg.intercept_)

reg.coef_は直線の傾きを表しています。この傾きのことを回帰係数と言ったりします。そしてreg.intercept_は直線の切片を表しています。つまり線形回帰をした結果、英語の点数は

上の式で予測できそうだということが分かりました。
最後に散布図の上に予測した直線を表示させてみましょう。

手順は先ほど散布図を作成したコードに直線を表示させるコードを付け加えればよいだけです。

# 横軸hour, 縦軸scoreの散布図を作成
plt.scatter(hour,score)
# 横軸hour, 縦軸scoreの予測値を使った直線を表示（色はグレー）
plt.plot(hour,reg.predict(hour),color="gray")
# 横軸のラベルをとしてStudy Hoursを表示
plt.xlabel("Study Hours")
# 縦軸のラベルをとしてEnglish Scoreを表示
plt.ylabel("English Score")
# 表示するx座標の範囲を指定（0～25までを表示）
plt.xlim(0,25)
# 表示するy座標の範囲を指定 (0～100までを表示)
plt.ylim(0,100)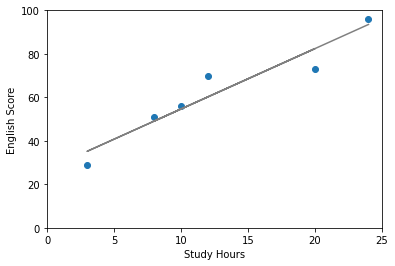

ということでできました。直線、曲線を表示したい場合はplt.plot(横軸のデータ, 縦軸のデータ)でできます。また()の中にcolor = “色の名前”を入れることでグラフの色を指定できます。今回はグレーにしてみました。

いかがでしたでしょうか。

今回の記事ではpythonを線形回帰について説明していきました。こんな感じでプログラミングを使えばいろいろなことができます。非常に興味深いですよね。

これからもこのようにプログラミングで色々やっていきたいと思います。ぼくが一番勉強になるので続けていきたいです！

最後までこの記事を読んでくれてありがとうございました。

この記事が役に立ったら幸いです。