こんにちは!しゅんです!
今回は最大マッチング問題について解説したいと思います!
この記事では最大マッチング問題を整数計画問題として定式化する方法、そしてそれをpythonで解く方法を解説しています。
それではやっていきましょう!
普段は組合せ最適化の記事を書いてたりします。
ぜひ他の記事も読んでみてください!
このブログの簡単な紹介はこちらに書いてあります。
興味があったら見てみてください。
このブログでは経営工学を勉強している現役理系大学生が、経営工学に関することを色々話していきます!
ぼくが経営工学を勉強している中で感じたことや、興味深かったことを皆さんと共有出来たら良いなと思っています。
そもそも経営工学とは何なのでしょうか。Wikipediaによると
経営工学(けいえいこうがく、英: engineering management)は、人・材料・装置・情報・エネルギーを総合したシステムの設計・改善・確立に関する活動である。そのシステムから得られる結果を明示し、予測し、評価するために、工学的な分析・設計の原理・方法とともに、数学、物理および社会科学の専門知識と経験を利用する。
引用元 : 経営工学 – Wikipedia
長々と書いてありますが、要は経営、経済の課題を理系的な観点から解決する学問です。
最大マッチング問題ってなに?
まず最初にそもそも最大マッチング問題がどんな問題なのかについて解説したいと思います。
マッチングってなに?
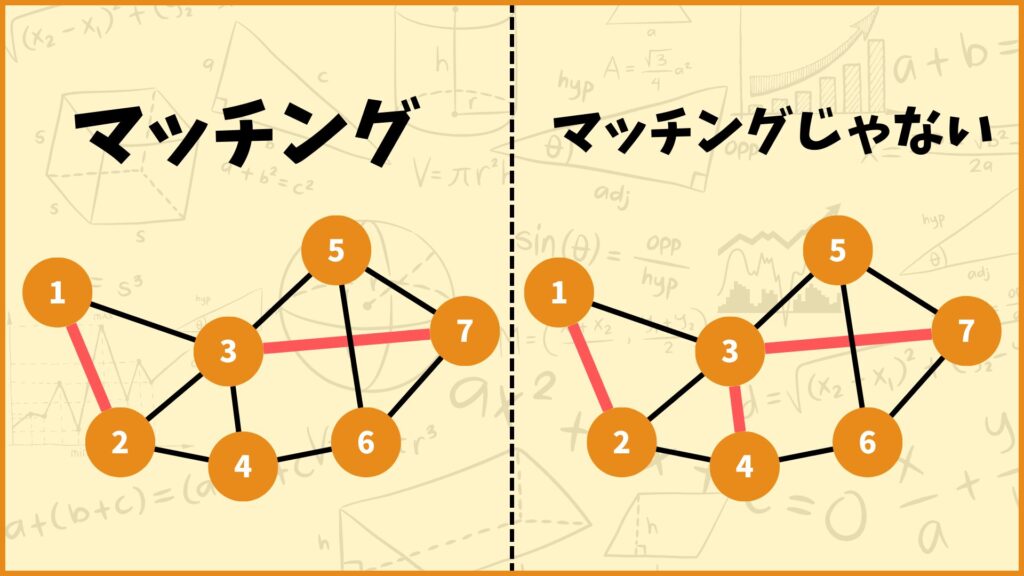
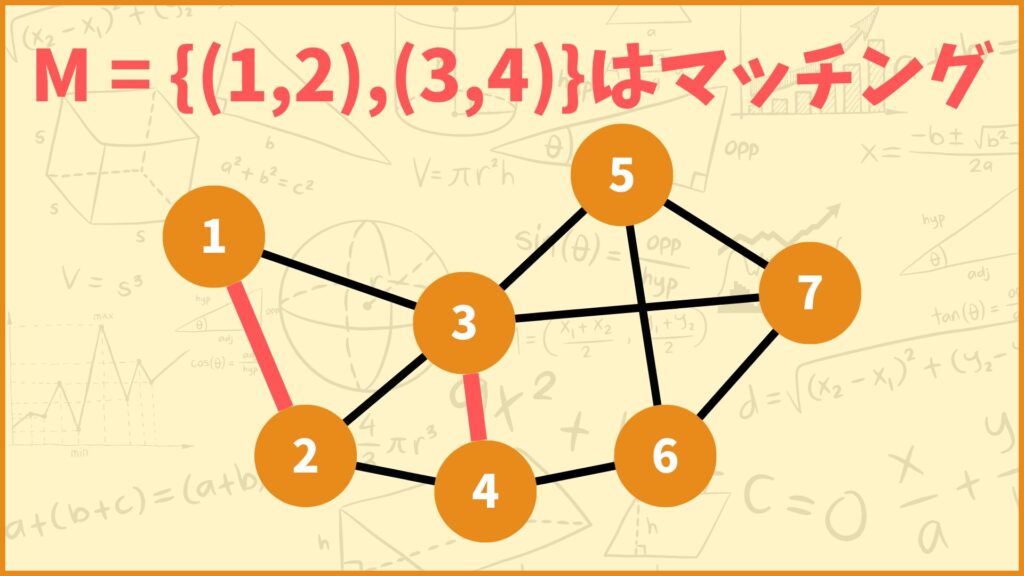
グラフからいくつか辺を選ぶときに、上図の左側の赤線を選んだらマッチングとなり、右側の赤線を選んだらマッチングとなりません。
マッチングを直観的に説明すると、頂点が被らないように辺を選んだらマッチング、頂点が被っていたらマッチングじゃないってことになります。上図の右側の選び方だと頂点3が被っているのでマッチングとはなりません。
数学的にちゃんと説明します。グラフの辺集合を\(E\)とすると、マッチングとは以下の条件を満たす\(E\)の部分集合\(M\)です。
「\(M\)中の任意の2つの要素\(e,e’\)に関して、\(e \cap e’ = \emptyset\)が成立する。但し辺\(e\)は要素数2の頂点集合とする。」
この説明を上図を使って理解してみましょう。上図の左側の場合\(M=\{\{1,2\},\{3,7\}\}\)となります。\(M\)中の要素\(\{1,2\},\{3,7\}\)について、\(\{1,2\} \cap \{3,7\} = \emptyset\)となるので\(M\)はマッチングとなります。
一方上図の右側の場合\(M = \{\{1,2\}, \{3,4\}, \{3,7\}\}\)となります。\(M\)中の要素\(\{1,2\},\{3,4\},\{3,7\}\)について、\(\{3,4\} \cap \{3,7\} = \{3\}\)となるので\(M\)はマッチングとなりません。
最大マッチングってなに?
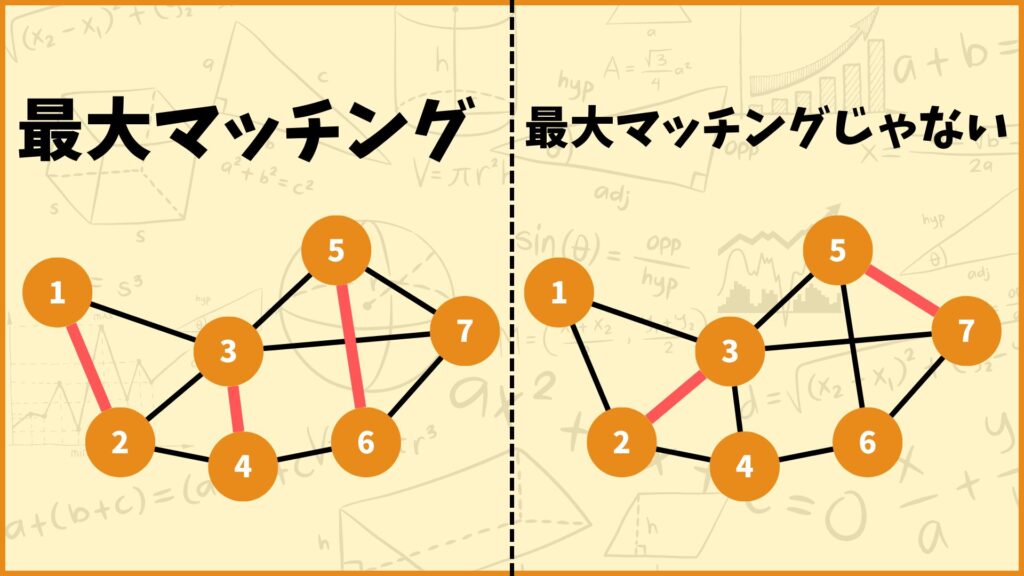
最大マッチングを直観的に説明すると、辺を一番多く選んだときのマッチングのことを最大マッチングと言います。例えば上図の左側は3本の辺を選んでいて、右側は2本の辺を選んでいます。
実はこのグラフは、マッチングとして最大でも3つの辺しか選ぶことができないため、左側のマッチングは最大マッチングとなります。
グラフが与えられたときに最大マッチングを求める問題が最大マッチング問題です。
数学的にちゃんと説明すると、最大マッチングとは要素数最大のマッチングのことを表します。
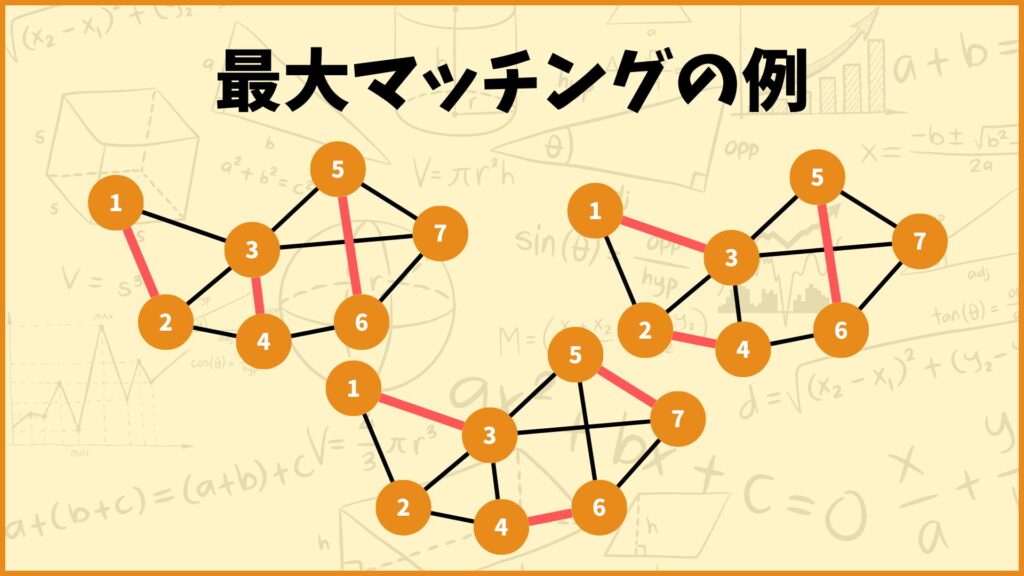
定義から分かるように、最大マッチングは複数存在する場合があります。例えばさっきのグラフだと上記のような最大マッチングが存在します。
日常で最大マッチング問題が登場する例
日常で最大マッチングが登場する例として、例えばジョブマッチングが挙げられます。ジョブマッチングは求職者と仕事をつなげることを指しますが、なるべく多くの人と仕事をつなげたいですよね。
ここで求職者と仕事を頂点と考え、求職者\(i\)が仕事\(j\)をできるとき辺\((i,j)\)が存在するようにすれば、この問題は最大マッチング問題とみなすことができます。

ちなみに上のグラフは2部グラフと呼ばれます。また2部グラフにおける最大マッチングを最大2部マッチングと呼びます。
最大マッチング問題を整数計画問題として定式化する
それでは次に最大マッチング問題を整数計画問題として定式化する方法を説明します。「記号の定義」、「目的関数の設定」、「制約条件の設定」の3つに分けてそれぞれ説明したいと思います。
記号の定義
パラメータ:
\(V\) : 頂点集合
\(E\) : 辺集合
\(\delta(i)\) : 頂点\(i\)に接続する辺の集合
変数:
\(x_{e} \in \{0,1\}\) : 辺\(e\)を選ぶなら1、選ばないなら0を取る0-1変数
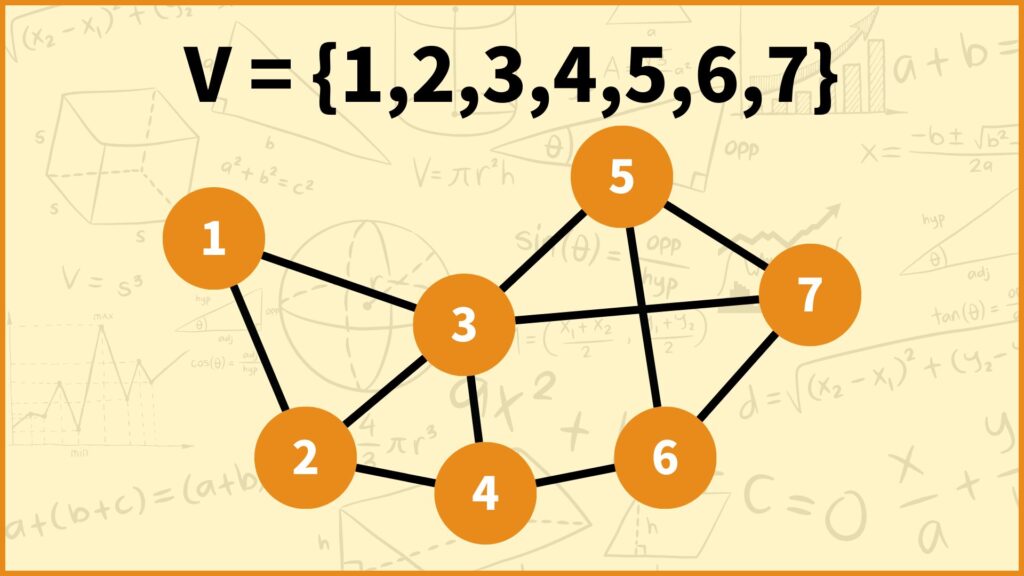
パラメータとして\(V,E,\delta(i)\)を設定します。\(V\)は頂点集合で、\(E\)は辺集合です。さっきの説明で用いた例だと
\(V = \{1,2,3,4,5,6,7\}\)
\(E = \{(1,2),(1,3),(2,3),(2,4),(3,4),(3,5),(3,7),(4,6),(5,6),(5,7),(6,7)\}\)
となります。
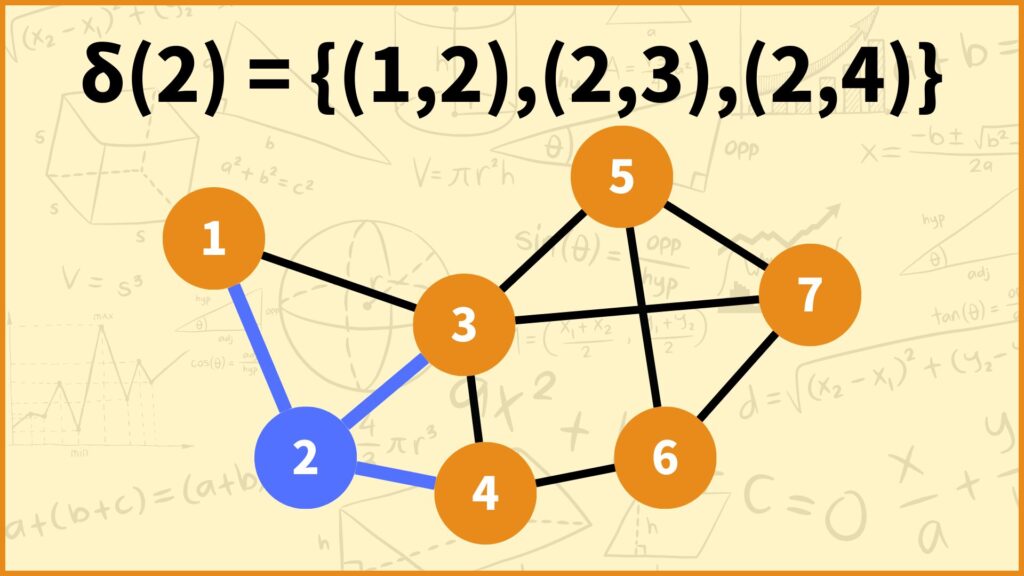
\(\delta(i)\)は頂点\(i\)に接続する辺の集合です。例えば頂点2に接続する辺は辺\((1,2),(2,3),(2,4)\)なので\(\delta(2) = \{(1,2),(2,3),(2,4)\}\)となります。
変数は辺\(e\)を選ぶなら1、選ばないなら0をとるような0-1変数\(x_e\)を用意します。
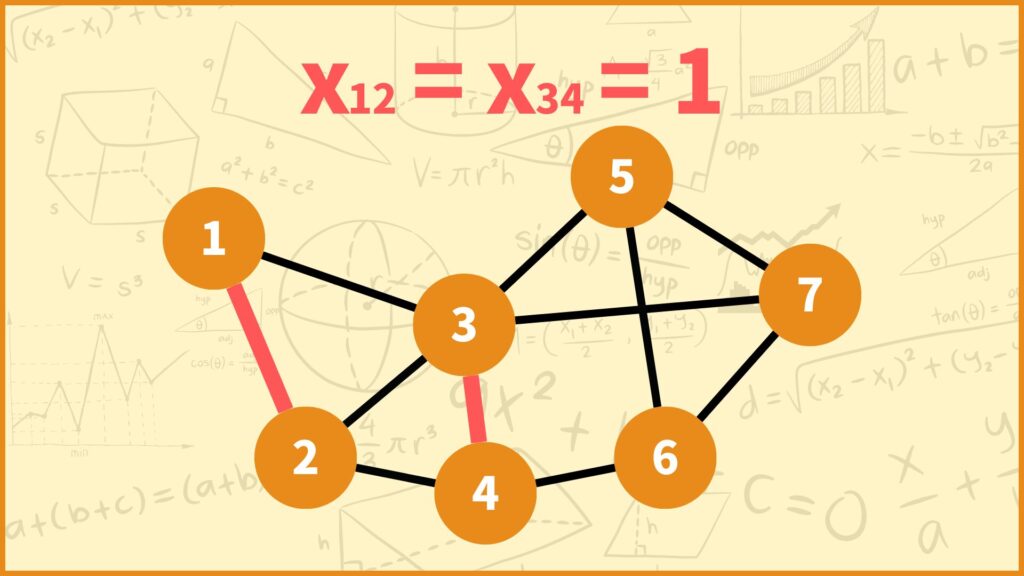
例えば上の例だと辺\((1,2),(3,4)\)を選んでいるので
\(x_{12} = x_{34} = 1\)
となります。
目的関数の設定
目的関数:
\(\sum\limits_{e \in E}x_e\)
最大マッチング問題の目的は
「マッチングの中で要素数が最大のものを求める」
というものです。
上のマッチングの例でいうと
\(x_{12} = x_{34} = 1\)
となるので目的関数値は
\(\sum\limits_{e \in E}x_{e} = x_{12} + x_{34} = 2\)
となり、これは上のマッチングの要素数と一致していますね。今回はこれが最大となる場合を求めたいので問題を\(\text{maximize}\)に設定します。
目的関数を最大化:
\(\max \;\; \sum\limits_{e \in E}x_{e}\)
制約条件の設定
制約条件:
\(\sum\limits_{e \in \delta(i)}x_e \leq 1 \;\;\; (\forall i \in V)\)
制約条件は
「選んだ辺からなる集合がマッチングになっている」
ということです。

例えば上図の左側の例を見てみましょう。これはマッチングですが、さっきの制約条件について考えてみると
\(x_{12} + x_{13} = 1\)
\(x_{12} + x_{23} + x_{24} = 1\)
\(x_{13} + x_{23} + x_{34} + x_{35} + x_{37} = 1\)
\(x_{24} + x_{34} + x_{46} = 0\)
\(x_{35} + x_{56} + x_{57} = 0\)
\(x_{46} + x_{56} + x_{67} = 0\)
\(x_{37} + x_{57} + x_{67} = 0\)
となり制約条件を満たしています。次に右側の例を見てみましょう。こっちは頂点3に接続する辺を2つ選んでいるのでマッチングではありませんが、頂点3に関してさっきの制約条件について考えてみると
\(x_{13} + x_{23} + x_{34} + x_{35} + x_{37} = x_{34} + x_{37} = 2\)
となり制約条件を満たしませんね。つまりこの制約条件は選んだ辺集合がマッチングであるための条件となっています。
制約条件:
\(\sum\limits_{e \in \delta(i)}x_e \leq 1 \;\;\; (\forall i \in V)\)
整数計画問題としてまとめる
以上のことを踏まえて整数計画問題として定式化しましょう。
パラメータ:
\(V\) : 頂点集合
\(E\) : 辺集合
\(\delta(i)\) : 頂点\(i\)に接続する辺の集合
変数:
\(x_e \in \{0,1\}\) : 辺\(e\)を選ぶなら1、選ばないなら0を取る0-1変数
定式化:
\( \max \;\;\; \sum\limits_{e \in E}x_e\)
\(\;\text{s.t.}\;\;\;\sum\limits_{e \in \delta(i)}x_e \leq 1 \;\;\; (\forall i \in V)\)
\(\;\;\;\;\;\;\;\;\; x_e \in \{0,1\} \;\;\; (\forall e \in E)\)
ということで整数計画問題として定式化することができました。
pythonで解いてみた
それでは実際にこの問題をpythonで解いてみましょう。結論以下のプログラムを実行することで問題を解くことができます。
## 事前準備
from pulp import * # pulpをインポート
## 記号の設定
V = [1,2,3,4,5,6,7] # 頂点集合の設定
E = [(1,2),(1,3),(2,3),(2,4),(3,4),(3,5),(3,7),(4,6),(5,6),(5,7),(6,7)] # 辺集合の設定
delta = {1:[(1,2),(1,3)],
2:[(1,2),(2,3),(2,4)],
3:[(1,3),(2,3),(3,4),(3,5),(3,7)],
4:[(2,4),(3,4),(4,6)],
5:[(3,5),(5,6),(5,7)],
6:[(4,6),(5,6),(6,7)],
7:[(3,7),(5,7),(6,7)]} # δ(i)の設定
## 整数計画問題として定式化して解く
prob = pulp.LpProblem(sense = LpMaximize) # 問題を最大化に設定
x = LpVariable.dicts("x",E, cat="Binary") # 変数の設定
prob += lpSum(x[e] for e in E) # 目的関数の設定
for i in V:
prob += lpSum(x[e] for e in delta[i]) <= 1 # 制約条件の設定
result = prob.solve() # 問題を解く
## 結果の表示
print("解の状態 :",LpStatus[result]) # 解の状態を表示(optimalなら最適解が得られてる)
print("最適値 :",prob.objective.value()) # 最適値の表示
for e in E:
if x[e].value() == 1:
print(f"x_{e} =", x[e].value()) # 最適解(値が1の変数)の表示
これらのプログラムを実行したら上の結果が得られました。それではコードが何を表しているのか1つずつ解説していきます。
コードの解説
「事前準備」、「記号の設定」、「整数計画問題として定式化して解く」、「結果の表示」の4つに分けてそれぞれ解説していきます。
事前準備
## 事前準備
from pulp import * # pulpのインポート
pulpはpythonで整数計画問題を扱うのに便利なライブラリです。インストールしていない場合はインストールする必要があります。
!pip install pulp # pulpのインストール 記号の設定
## 記号の設定
V = [1,2,3,4,5,6,7] # 頂点集合の設定
E = [(1,2),(1,3),(2,3),(2,4),(3,4),(3,5),(3,7),(4,6),(5,6),(5,7),(6,7)] # 辺集合の設定
delta = {1:[(1,2),(1,3)],
2:[(1,2),(2,3),(2,4)],
3:[(1,3),(2,3),(3,4),(3,5),(3,7)],
4:[(2,4),(3,4),(4,6)],
5:[(3,5),(5,6),(5,7)],
6:[(4,6),(5,6),(6,7)],
7:[(3,7),(5,7),(6,7)]} # δ(i)の設定
2行目で頂点集合をリスト形式で設定しています。今回は頂点1から頂点7まであるので上のようなリストを作成しました。
3行目で辺集合をリスト形式で設定しています。
4~10行目で各頂点のコストを辞書形式で設定しています。
整数計画問題として定式化して解く
## 整数計画問題として定式化して解く
prob = pulp.LpProblem(sense = LpMaximize) # 問題を最大化に設定
x = LpVariable.dicts("x",E, cat="Binary") # 変数の設定
prob += lpSum(x[e] for e in E) # 目的関数の設定
for i in V:
prob += lpSum(x[e] for e in delta[i]) <= 1 # 制約条件の設定
result = prob.solve() # 問題を解く
2行目で問題を最大化に設定しています。「sense = LpMinimize」だと目的関数を最小化する問題に設定できます。
4行目で変数を設定しています。「LpVariable.dicts()」は変数をいっぺんに設定できるので変数が多いときに便利です。括弧の中身は左から順に(”変数名”, 添字の集合, 変数の種類)となっています。
変数\(x_e\)の添字\(e\)は辺集合\(E\)中の要素なので添字の集合はEとします。
「cat = “Binary”」で変数を0-1変数に設定しています。連続変数にしたければ「cat = “Continuous”」とすれば良いです。
6行目で目的関数を設定しています。pulpで\(\sum\)は「lpSum」で表現できます。「x[e]」と設定することで\(x_e\)、「for e in E」と設定することで\(e \in E\)を表現できます。
8~9行目で制約条件を設定しています。「for i in V」で\(\forall i \in V\)を表しています。
「prob += lpSum(x[e] for e in delta[i]) <= 1」で\(\sum\limits_{e \in \delta(i)}x_e \leq 1\)を表しています。
11行目で問題を解いています。問題を解くときは「.solve()」でできます。
結果の表示
## 結果の表示
print("解の状態 :",LpStatus[result]) # 解の状態を表示(optimalなら最適解が得られてる)
print("最適値 :",prob.objective.value()) # 最適値の表示
for e in E:
if x[e].value() == 1:
print(f"x_{e} =", x[e].value()) # 最適解(値が1の変数)の表示
2行目で解の状態を表示しています。Optimalと表示されたら最適解が得られています。
3行目で最適値を表示しています。
4~6行目で最適解を表示しています。値が1の変数だけ表示するようにしています。
結果の解釈

上記のプログラムを実行したら上のような結果が得られました。1つずつ見ていきます。
1行目は解の状態を表しています。Optimalと表示されているので最適解が得られています。
2行目は最適値を表しています。今回の最大マッチング問題の最適値は3であることが分かりました。
3~5行目は最適解を表しています。これを見ると辺(1,3),(2,4),(6,7)を選ぶのが最適であることが分かります。
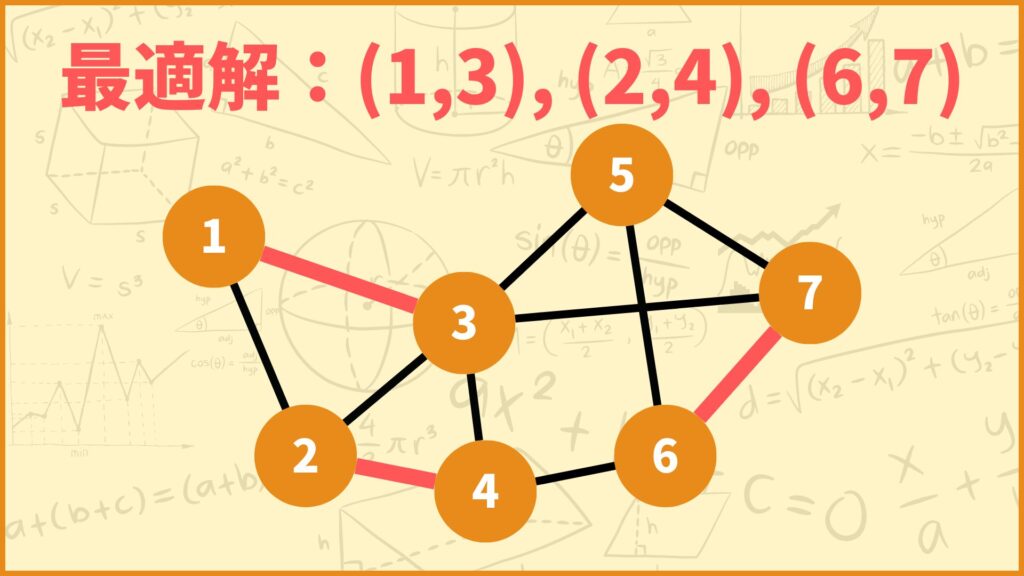
確かにマッチングになっていますね。頂点数が7個なので要素数が4以上のマッチングが存在しないことが分かります。
頂点数をもっと増やしてみた
それでは最後に頂点数をもっと増やして最大マッチング問題を解いてみたいと思います。
グラフを描画してみた
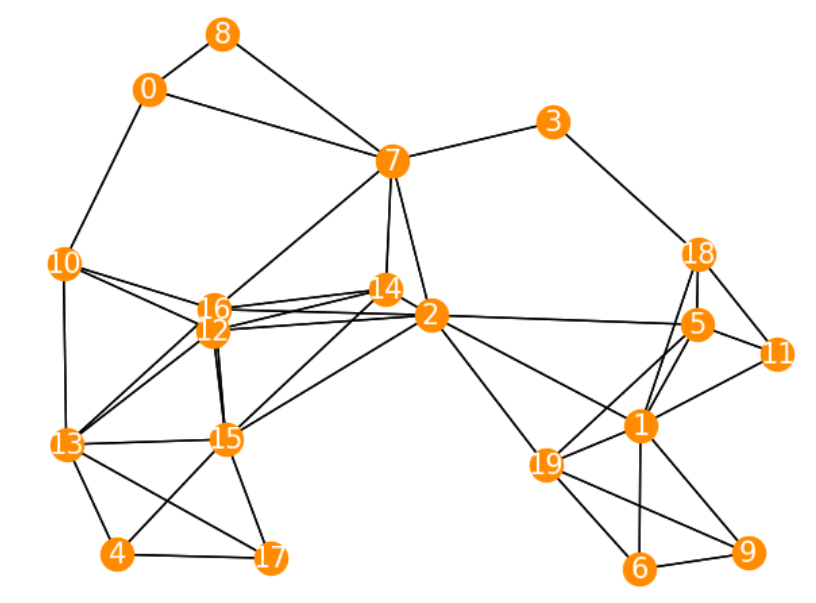
頂点数は20個、各頂点は\([0,10] \times [0,10]\)の2次元ユークリッド平面上にランダムに配置しました。また頂点\(i\)と頂点\(j\)間のユークリッド距離が3.5以下の場合に辺\((i,j)\)が存在するようにしました。
上のグラフを表示するコードは以下の通りです。本題ではないので説明は省略します。
import networkx as nx # networkxのインポート
import matplotlib.pyplot as plt # matplotlibのインポート
import random # randomのインポート
random.seed(1) # ランダム値の固定
V = [i for i in range(20)] # 頂点集合を設定(頂点数は20)
E = [] # 辺集合の初期設定
delta = {} # δ(i)の初期設定
for i in V:
delta[i] = []
Pos = {} # 各頂点の座標の初期設定
for i in V:
Pos[i] = [random.uniform(0,10),random.uniform(0,10)] # 各頂点の座標を[0,10]×[0,10]上の2次元ユークリッド平面上にランダムに配置
# グラフの初期化
G = nx.DiGraph()
# 頂点を追加
for v, pos in Pos.items():
G.add_node(v, pos=pos)
# 辺を追加
for i in V:
for j in V:
if i < j:
if ((Pos[i][0] - Pos[j][0])**2 + (Pos[i][1] - Pos[j][1])**2)**(1/2) <= 3.5: # 距離が3.5以下の辺だけグラフに追加
G.add_edge(i, j)
E.append((i,j))
# δ(i)の設定
for i in V:
for j in V:
if (i,j) in E:
delta[i].append((i,j))
elif (j,i) in E:
delta[i].append((j,i))
# グラフの描画
pos = nx.get_node_attributes(G, 'pos')
nx.draw(G, pos, with_labels=True, node_color='darkorange', node_size=300,font_size = 15, font_color="white", arrows = False, edge_color = "black")
plt.show()最大マッチング問題を解いてみた
コードはさっきと全く一緒です。
## 整数計画問題として定式化して解く
prob = pulp.LpProblem(sense = LpMaximize) # 問題を最大化に設定
x = LpVariable.dicts("x",E, cat="Binary") # 変数の設定
prob += lpSum(x[e] for e in E) # 目的関数の設定
for i in V:
prob += lpSum(x[e] for e in delta[i]) <= 1 # 制約条件の設定
result = prob.solve() # 問題を解く
## 結果の表示
print("解の状態 :",LpStatus[result]) # 解の状態を表示(optimalなら最適解が得られてる)
print("最適値 :",prob.objective.value()) # 最適値の表示
for e in E:
if x[e].value() == 1:
print(f"x_{e} =", x[e].value()) # 最適解(値が1の変数)の表示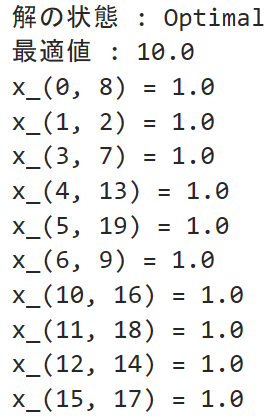
最大マッチング問題を解いたら上のような結果が得られました。最適値が10なので計10個の辺を選んだらしいです。3行目からはマッチングとして選んだ辺を表示していますが、多すぎてよく分からないので図示してみましょう。
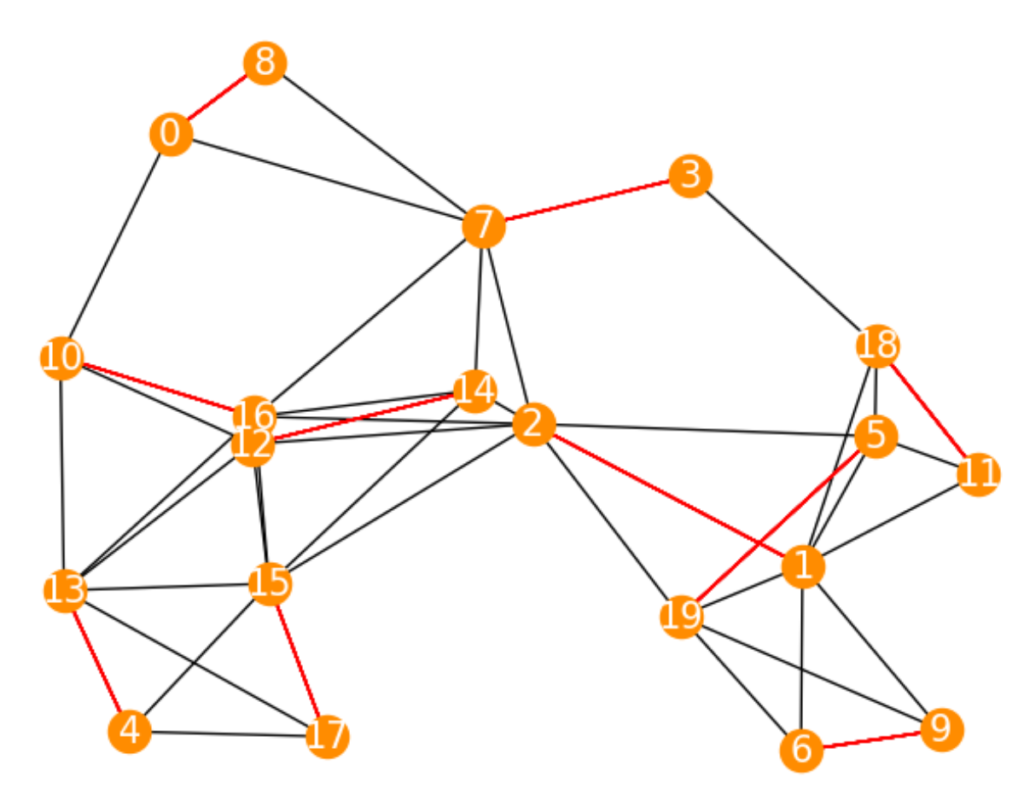
選ばれた辺は赤色にしました。上記のマッチングが要素数最大のマッチングだと分かりました。
上のグラフを描画するコードは以下の通りです。
# グラフの初期化
G = nx.DiGraph()
# 頂点を追加
for v, pos in Pos.items():
G.add_node(v, pos=pos)
# 辺を追加
for i in V:
for j in V:
if i < j:
if ((Pos[i][0] - Pos[j][0])**2 + (Pos[i][1] - Pos[j][1])**2)**(1/2) <= 3.5:
G.add_edge(i, j)
E.append((i,j))
# グラフの描画
pos = nx.get_node_attributes(G, 'pos')
nx.draw(G, pos, with_labels=True, node_color='darkorange', node_size=300,font_size = 15, font_color="white", arrows = False, edge_color = "black")
for e in E:
if x[e].value() == 1:
nx.draw_networkx_edges(G, pos, edgelist=[e], edge_color='red', arrows = False)
plt.show()ちなみに上のグラフは20個の頂点から構成され、最大マッチングの要素数は10なので、グラフ中のどの点も得られたマッチング中のいずれかの辺と接続していることが分かります。このようなマッチングを完全マッチングと言います。
おわりに
いかがでしたか。
今回の記事では頂点被覆問題について解説していきました。
今後もこのような組合せ最適化に関する記事を書いていきます!
最後までこの記事を読んでくれてありがとうございました。



