こんにちは!しゅんです!
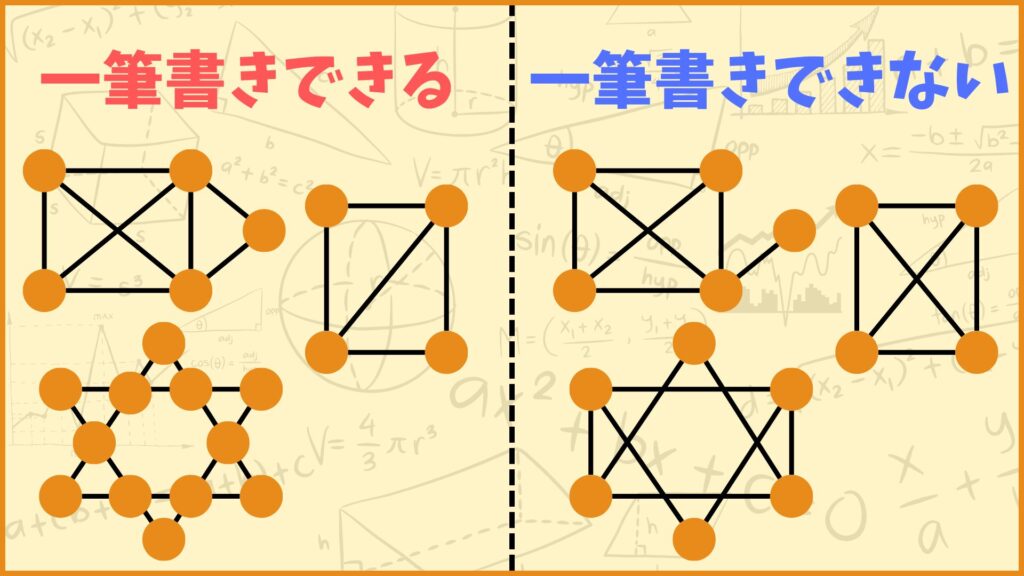
いきなりですが、下の図は一筆書きで描くことができるでしょうか?
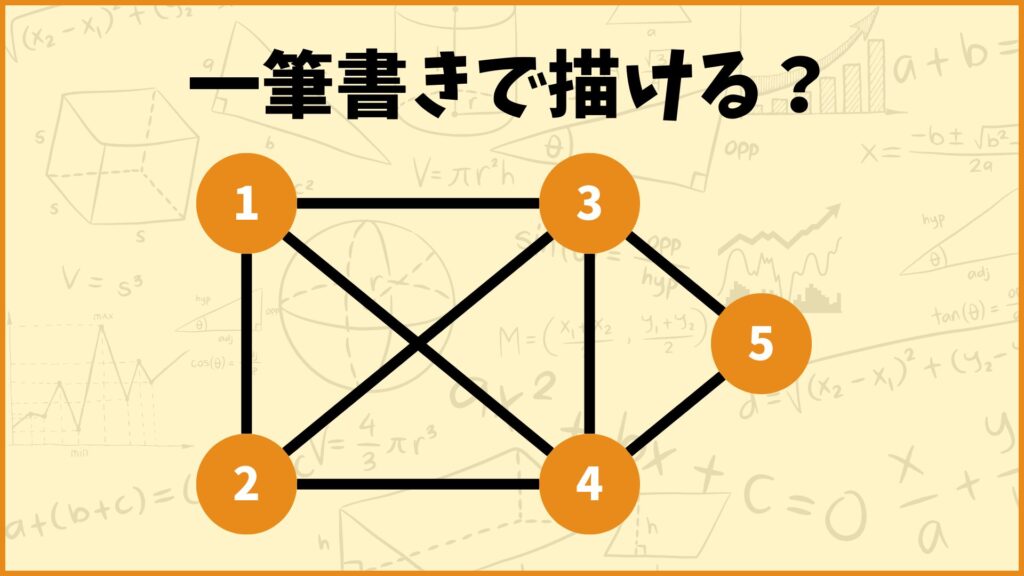
この記事ではどんな図形なら一筆書きできるのかについて、数学を使って説明してみたいと思います!
ややこしい数式は一切使いません!!!
それではやっていきましょう!
普段は組合せ最適化の記事を書いてたりします。
ぜひ他の記事も読んでみてください!
このブログの簡単な紹介はこちらに書いてあります。
興味があったら見てみてください。
このブログでは経営工学を勉強している現役理系大学生が、経営工学に関することを色々話していきます!
ぼくが経営工学を勉強している中で感じたことや、興味深かったことを皆さんと共有出来たら良いなと思っています。
そもそも経営工学とは何なのでしょうか。Wikipediaによると
経営工学(けいえいこうがく、英: engineering management)は、人・材料・装置・情報・エネルギーを総合したシステムの設計・改善・確立に関する活動である。そのシステムから得られる結果を明示し、予測し、評価するために、工学的な分析・設計の原理・方法とともに、数学、物理および社会科学の専門知識と経験を利用する。
引用元 : 経営工学 – Wikipedia
長々と書いてありますが、要は経営、経済の課題を理系的な観点から解決する学問です。
どんな図形なら一筆書きできるの?
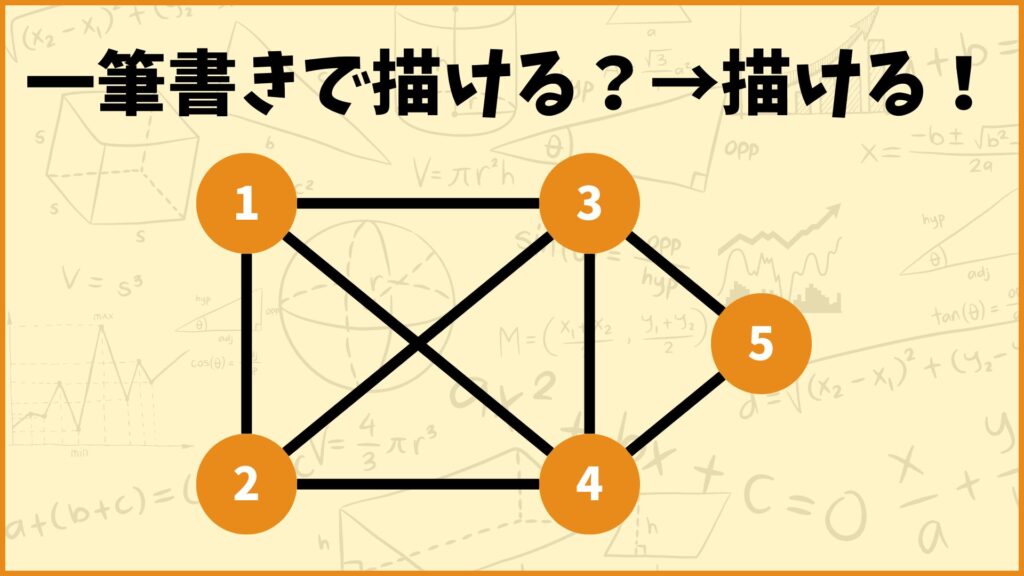
さっそく本題に入りましょう。結論図形が一筆書きできるかどうかはオレンジ色の丸にくっついている黒い線の数によって決まります。
説明のためにこれ以降オレンジ色の丸を頂点、黒線を辺と呼びます。
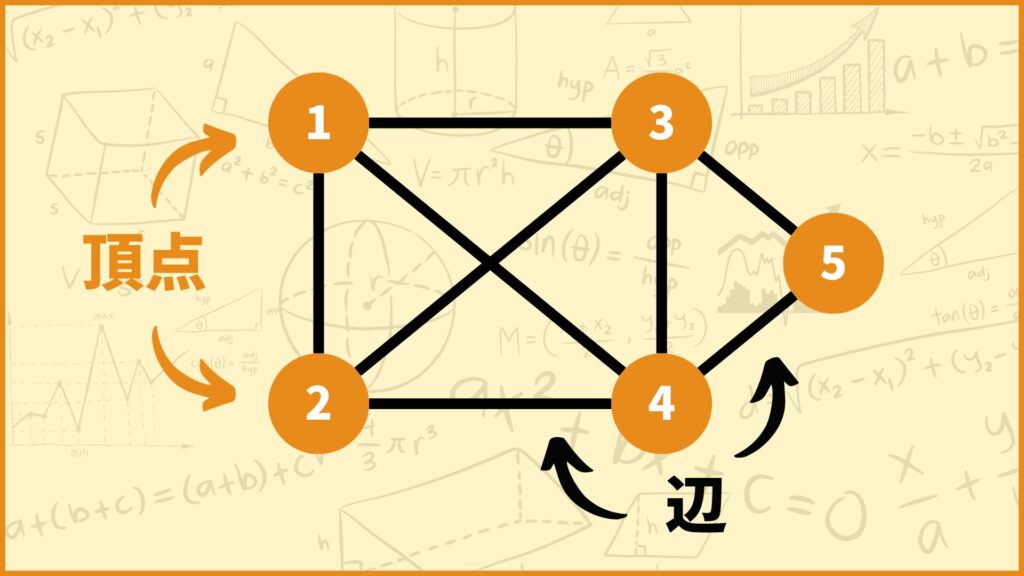
上の図で言うと例えば頂点1には3つの辺がくっついていますね。全ての頂点についてこのように考えていくと
頂点1にくっついている辺の数 : 3本
頂点2にくっついている辺の数 : 3本
頂点3にくっついている辺の数 : 4本
頂点4にくっついている辺の数 : 4本
頂点5にくっついている辺の数 : 2本
となります。これを見ると各頂点にくっついている辺の数は、頂点1,2に関しては奇数、頂点3,4,5に関しては偶数となっています。
実はこのパターンだと一筆書きできるんです!
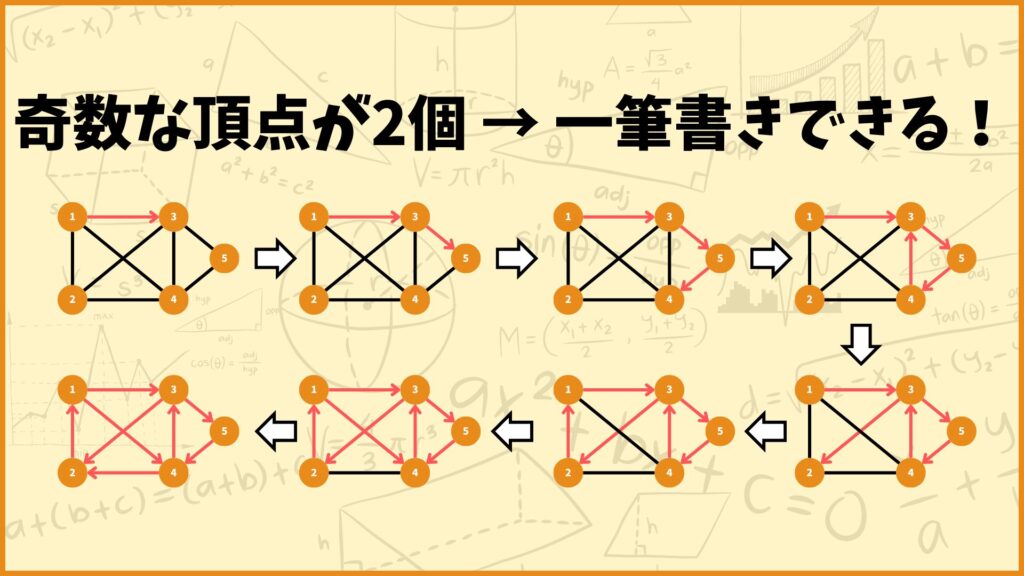
一筆書きができる条件は
「くっついている辺の数が奇数である頂点が0個または2個」
です。上の例の場合はくっついている辺の数が奇数である頂点が2個だったので一筆書きできます。
数学を使って詳しく説明する
ここまでは数学用語を使わずに説明していきましたが、ここからは数学用語を使って説明していきたいと思います。一筆書きについて詳しく考えてみたい人はぜひ読んでみてください!
グラフってなに?
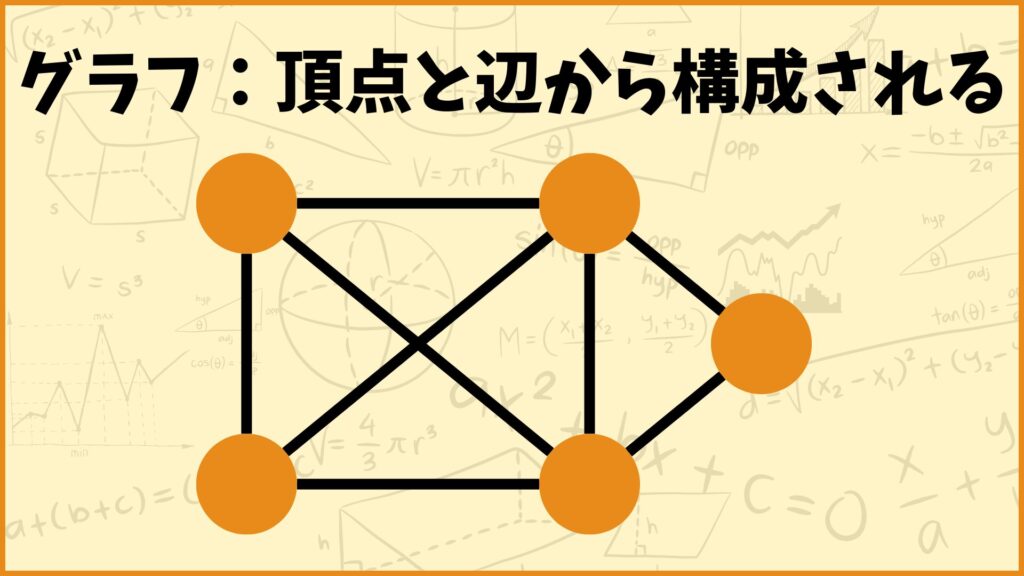
今回考えているような図はグラフと呼ばれます。超簡単に説明するとグラフとは頂点と辺から構成される上図のようなもののことです。
グラフには色々種類があります。例えば辺に向きがあるかないか、辺に重みがあるかないか、頂点数は有限か無限かなどで分類することができます。このようにグラフについてどんな性質があるかを考える学問をグラフ理論と言います。
グラフ理論ではよく頂点を\(v\)、辺を\(e\)と表します。
接続、次数ってなに?
グラフ中のある頂点\(v\)とある辺\(e\)がくっついていることを「\(v\)と\(e\)は接続する」と言います。また、グラフ中のある頂点\(v\)に接続する辺の本数を次数と言います。
次数は\(\text{deg}(v)\)と書いたりします。
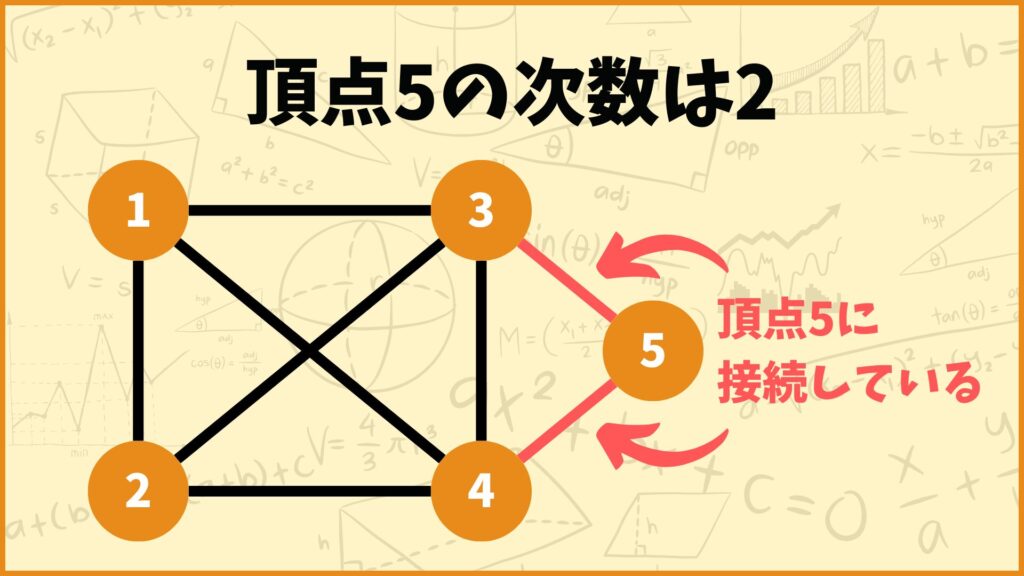
例えば上のグラフの頂点5について考えてみましょう。頂点5には2つの辺が接続しています。(赤く塗っている辺です)そのため頂点5の次数は2となります。
辺の名前は接続している両端の頂点によって決まります。例えば頂点3と頂点5の間を結ぶ辺は辺\((3,5)\)と書きます。
路ってなに?
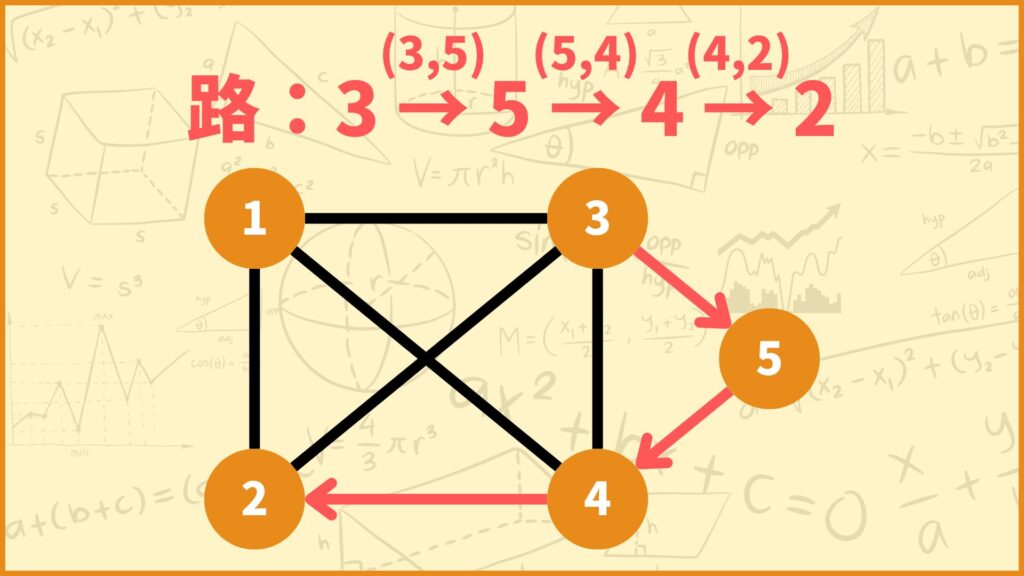
頂点、辺、頂点、辺、…という風に頂点と辺が交互に登場する列を路と言います。(路の最初と最後は必ず頂点になります)
例えば上の例で言うと、赤で塗った路は
頂点3→辺(3,5)→頂点5→辺(5,4)→頂点4→辺(4,2)→頂点2
という路となります。
列\(v_0,e_1,v_1,e_2,…,e_k,v_k\)が路であるためには\(e_i\)の端点(列において\(e_i\)の1個前と1個後の頂点)が\(v_{i-1}\)と\(v_i\)である必要があります。
超簡単に言うと繋がっていないと路とは言わないってことです。
オイラー路ってなに?
オイラー路:
グラフ中のすべての辺を丁度1度通るような路
グラフ理論の言葉にオイラー路というものがあります。オイラー路は全ての辺を丁度1度通るような路です。
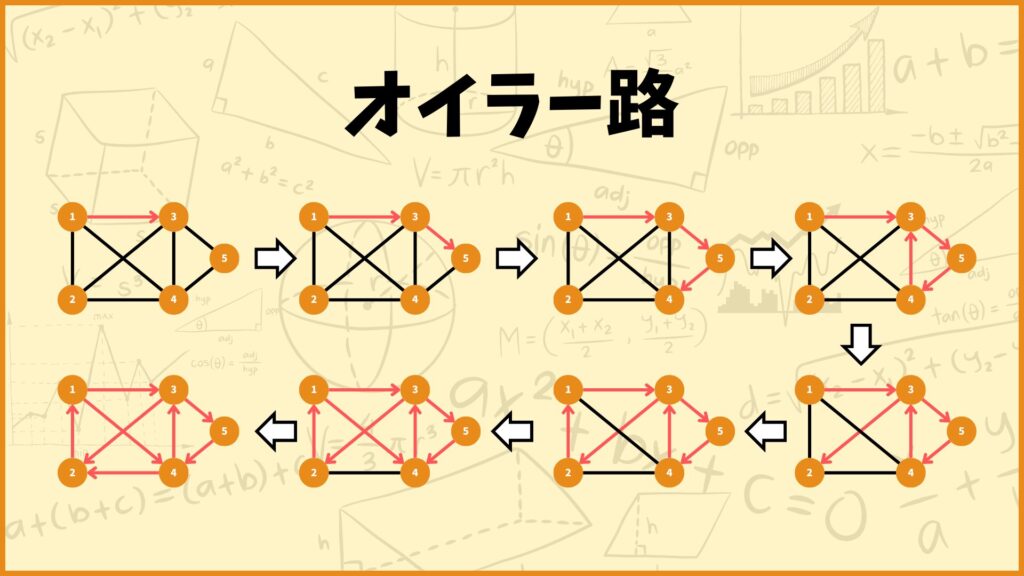
例えば上のグラフには上記のようなオイラー路が存在します。実はこれ、一筆書きと同じことを表しています。
オイラー路と一筆書きは同じ!
そのため「グラフの一筆書きができるか」という問題は「グラフにオイラー路は存在するか」という問題に書き換えることができます。
オイラー路が存在する条件ってなに?
(連結な無向)グラフにオイラー路が存在する(必要十分)条件:
次数が奇数の頂点数が0個または2個である。
実はグラフにオイラー路が存在する条件は、次数が奇数の頂点の数が0個または2個であることが知られています。

上図の左側にあるグラフは全て次数が奇数の頂点数が0個or2個なのでオイラー路が存在します。つまり一筆書きができるという訳です。逆に右側にあるグラフは次数が奇数の頂点数が0個or2個ではないのでオイラー路が存在しません。つまり一筆書きができません。
全ての辺を丁度一度通る路はオイラー路ですが、全ての頂点を丁度一度通る路はハミルトン路と呼ばれます。
オイラー路とハミルトン路はこちらの記事で詳しく解説しています!
おわりに
いかがでしたか。
今回の記事では一筆書きとグラフ理論について解説していきました。
今後もこのようなグラフ理論に関する記事を書いていきます!
最後までこの記事を読んでくれてありがとうございました。




