こんにちは!しゅんです!
今回は整数計画問題として定式化してアルバイトのシフト作成をしていきたいと思います!
シフトを作成するのって色々制約があって大変ですよね。この記事では条件を全て満たし、かつみんなが納得するようなシフト作成の方法を解説していきます!
このテーマは
・結果の解釈 ← 今回はここ!
・問題の設定と定式化の解説
・pythonで実装する方法の解説
の3つの記事に分かれています!
問題の設定と定式化の解説はこちらから!
pythonで実装する方法はこちらから!
それでは解説していきましょう!
普段は統計検定2級の記事を書いてたりします。
ぜひ他の記事も読んでみてください!
このブログの簡単な紹介はこちらに書いてあります。
興味があったら見てみてください。
このブログでは経営工学を勉強している現役理系大学生が、経営工学に関することを色々話していきます!
ぼくが経営工学を勉強している中で感じたことや、興味深かったことを皆さんと共有出来たら良いなと思っています。
そもそも経営工学とは何なのでしょうか。Wikipediaによると
経営工学(けいえいこうがく、英: engineering management)は、人・材料・装置・情報・エネルギーを総合したシステムの設計・改善・確立に関する活動である。そのシステムから得られる結果を明示し、予測し、評価するために、工学的な分析・設計の原理・方法とともに、数学、物理および社会科学の専門知識と経験を利用する。
引用元 : 経営工学 – Wikipedia
長々と書いてありますが、要は経営、経済の課題を理系的な観点から解決する学問です。
整数計画問題として問題を作成
今回はシフト作成問題を整数計画問題として、目的関数と制約条件を設定したいと思います。簡単に言うと変数が取りうる値が整数の問題です。整数計画問題としてはナップサック問題が有名です。
ナップサック問題はこちらの記事で説明しています!

それでは1つずつ解説していきましょう!
問題設定を決める
まず最初に今回考える問題を設定していきます。今回は以下のように設定したいと思います。
今回考える問題
・あるアルバイトの1週間分のシフトを決める。(このシフトは1カ月使う)
・アルバイトの希望賃金との差がなるべく小さくなるようにシフトを作る
・アルバイト生は合計16人である。
・シフトの種類は日勤(d)、準夜勤(e)、深夜勤(n)の3つがある。
・各シフトの情報は以下の通りである。

制約条件を決める
次に考慮しなければいけない条件を設定します。まず最初に列挙してその後1つずつ解説していきます。
考慮する制約条件
・1日のシフトは最大1つまで
・深夜勤→日勤、深夜勤→準夜勤、準夜勤→日勤は禁止
・1週間のシフト数は最大5個まで
・深夜勤は最大3連勤まで
1日のシフトは最大1つまで
例えば8:00~16:00まで日勤でバイトした後に続けて準夜勤、夜勤をすることを禁止します。また準夜勤でバイトしたときはその日の日勤と深夜勤はできません。また深夜勤でバイトしたときはその日の日勤と準夜勤はできません。
深夜勤は24:00~8:00なので時間的には次の日になりますが、ここでは日勤、準夜勤、深夜勤を1日のシフトの集合として考えています。

深夜勤→日勤、深夜勤→準夜勤、準夜勤→日勤は禁止
これも働きすぎを制限する条件です。


※準夜勤→深夜勤は「1日のシフトは最大1つまで」で制限しています。
1週間のシフト数は最大5個まで
これは何連勤もするのを防ぐための条件です。

6回働いてしまうと、どう頑張っても6連勤になってしまうのでそれは禁止します。
深夜勤は最大3連勤まで
最大でも深夜勤は3連勤までにします。4連勤でなければ1週間に4回以上深夜勤しても大丈夫です。

これらの条件を数式を使って表していきたいと思います。
問題を数式で表す
それでは問題を数式で表してみます。結論以下のように定式化できます。
\(P=\{1,2,…,16\}\):アルバイト生\(i\)の集合
\(D=\{1,2,…,7\}\):曜日\(j\)の集合
\(S=\{d,e,n\}\):シフト\(k\)の集合
\(w_k \; (k \in S)\):シフト\(k\)の時給
\(np_k \; (k \in S)\) : シフト\(k\)での必要人数
\(e_i \; (i \in P)\):アルバイト生\(i\)の希望賃金
\(\text{min} \;\;\;\;\;\;t\)
\(\text{s.t.}\;\;\sum\limits_{j \in D,k \in S}8w_kx_{ijk}-e_i \leq t\;\;\;\;\; i \in P\)
\(\;\;\;\;\;\;\;e_i-\sum\limits_{j \in D,k \in S}8w_kx_{ijk} \leq t\;\;\;\;\; i \in P\)
\(\;\;\;\;\;\;\;\sum\limits_{i \in P}x_{ijk}=np_k\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\; j \in D,\; k \in S\)
\(\;\;\;\;\;\;\;\sum\limits_{k \in S}x_{ijk} \leq 1 \;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\; i \in P, \; j \in D\)
\(\;\;\;\;\;\;\;x_{ije}+x_{i(j+1)_{\text{mod}7}d} \leq 1\;\;\;\;\;\;\;\; i \in P,\; j \in D\)
\(\;\;\;\;\;\;\;x_{ijn}+x_{i(j+1)_{\text{mod}7}d} \leq 1\;\;\;\;\;\;\;\; i \in P,\; j \in D\)
\(\;\;\;\;\;\;\;x_{ijn}+x_{i(j+1)_{\text{mod}7}e} \leq 1\;\;\;\;\;\;\;\; i \in P,\; j \in D\)
\(\;\;\;\;\;\;\;\sum\limits_{j \in D,k \in S}x_{ijk} \leq 5 \;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\; i \in P\)
\(x_{ijn}+x_{i(j+1)_{\text{mod}7}n}+x_{i(j+2)_{\text{mod}7}n}+x_{i(j+3)_{\text{mod}7}n} \leq 3\;\;\;\;\;i \in P,\; j \in D\)
数式はこちらの記事で詳しく解説しています!
問題をpythonで解く
最後にこの問題をpythonを使って解いてみたいと思います。コードの説明は下の記事で解説しているので、ここではコードの解説は飛ばして結果の解釈をしていきたいと思います。
現在制作中
結論以下のコードを実行することでシフトを作成することができます。
## 事前準備
# pulpをインポート
! pip install pulp
from pulp import *
# numpyをインポート
import numpy as np
# ppprintをインポート
import pprint
# ランダムな値を固定する
np.random.seed(100)
## 問題の設定
# 問題を最小化に設定する
prob = LpProblem(sense=LpMinimize)
# 集合の定義
P = {i for i in range(16)} # バイトの集合
D = {i for i in range(7)} # 曜日の集合
S = {"d", "e", "n"} # シフトの集合
# パラメータの定義
NumP = {"d":4, "e":3, "n":2} # 各シフトに必要な人数のパラメータ
E = dict(zip(P,np.random.randint(20000, 80000, 16))) # 各バイトの希望賃金のパラメータ
W ={"d":1000, "e":1200, "n":1500} # 各シフトの時給のパラメータ
# 変数の定義
x = pulp.LpVariable.dicts("x",(P,D,S), cat=LpBinary)
t = pulp.LpVariable("t", cat = LpContinuous)
# 目的関数の設定
prob += t
# 制約条件の設定
# 目的関数を混合最適計画問題に表現したことによって生じた制約
for i in P:
prob += lpSum(8*W[k] * x[i][j][k] for j in D for k in S) - E[i] <= t
prob += E[i] - lpSum(8*W[k] * x[i][j][k] for j in D for k in S) <= t
# 各シフトの必要人数を満たす
for j in D:
for k in S:
prob += lpSum(x[i][j][k] for i in P) == NumP[k]
# 1日のシフトは1個まで
for i in P:
for j in D:
prob += lpSum(x[i][j][k] for k in S) <= 1
# 準夜勤→日勤を禁止
for i in P:
for j in D:
prob += x[i][j]["e"] + x[i][(j+1)%7]["d"] <= 1
# 夜勤→日勤を禁止
for i in P:
for j in D:
prob += x[i][j]["n"] + x[i][(j+1)%7]["d"] <= 1
# 夜勤→純夜勤を禁止
for i in P:
for j in D:
prob += x[i][j]["n"] + x[i][(j+1)%7]["e"] <= 1
# 勤務日数は最大5日まで
for i in P:
prob += lpSum(x[i][j][k] for j in D for k in S) <= 5
# 深夜勤は最大3連勤まで
for i in P:
for j in D:
prob += x[i][j]["n"] + x[i][(j+1)%7]["n"] + x[i][(j+2)%7]["n"] + x[i][(j+3)%7]["n"] <= 3
prob.solve() # 問題を解く
# 結果を表示
print(LpStatus[prob.status]) # 解の状態を表示(Optimalなら最適解が求められている)
print("Optimal Value =", value(prob.objective)) # 最適値を表示
# シフトを2次元リストで表す
data = [[] for i in range(len(P))]
for i in P:
for j in D:
if value(x[i][j]["d"]) == 1:
data[i].append("日")
elif value(x[i][j]["e"]) == 1:
data[i].append("準")
elif value(x[i][j]["n"]) == 1:
data[i].append("深")
else:
data[i].append("×")
pprint.pprint(data)このコードを実行すると以下のような結果が得られました。
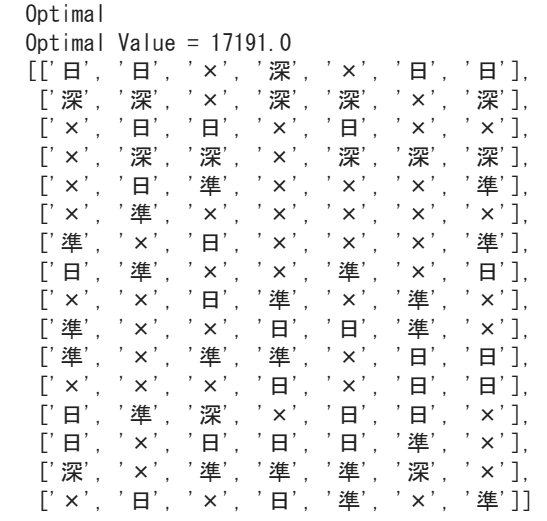
この2次元リストは行がバイト\(i\)、列が\(j\)曜日、日勤なら「日」、準夜勤なら「準」、深夜勤なら「深」、休みなら「×」で表しています。
例えばアルバイト1の1週間の勤務スケジュールは
月曜日:日勤
火曜日:日勤
水曜日:休み
木曜日:深夜勤
金曜日:休み
土曜日:日勤
日曜日:日勤
となっています。ちゃんと週5日の制約になっています。他にも深夜勤の次の日は休みを満たしていますね。
他にも例えば月曜日の列を見ると
日勤:
バイト1、バイト8、バイト13、バイト14
準夜勤:
バイト7、バイト10、バイト11
深夜勤:
バイト2、バイト15
となっていてちゃんと人数の制約条件も満たしていますね。
結果の解釈
Optimal Valueは\(t\)の最小値を表しています。この\(t\)は希望賃金との差が最も大きい人の値を最小化するように設定しています。

今回は17191なので、最大でも17191円以上希望賃金と差があるバイト生はいないことを表しています。各バイト生の希望賃金を見てみましょう。

これを見るとバイト3の希望賃金が77191で最も高いですね。バイト3は5日間深夜勤をするので、合計60000円稼ぎます。希望賃金との差は77191-60000=17191円なので最も希望賃金と差があるのはバイト3ということが分かります。
得られたシフトの改善点
最後にこのシフトの改善点について考えてみたいと思います。もう一度バイト3の希望賃金とシフトを見てみましょう。
pythonでは数字は0から始まるのでバイト3は上から4番目の列のシフトです。
これを見ると5日間深夜勤していますね。他にもバイト1(2列目)が5日間深夜勤、バイト14(15行目)が2日間準夜勤、3日間深夜勤をするシフトになっています。

ちょっと準夜勤、深夜勤が特定のバイト生に偏りすぎだと感じます。希望賃金が高い人たちがこのような傾向になっています。
もう少し希望賃金の上限を低く設定するとより良いシフトを作成できるかもしれません。
おわりに
いかがでしたか。
今回の記事ではシフト作成問題について解説していきました。
今後もこのような経営工学に関する記事を書いていきます!
最後までこの記事を読んでくれてありがとうございました