こんにちは!しゅんです!
今回は整数計画問題として定式化したアルバイトのシフト作成問題をpythonで解いいきたいと思います!
シフトを作成するのって色々制約があって大変ですよね。この記事では条件を全て満たし、かつみんなが納得するようなシフト作成の方法を解説していきます!
このテーマは
・結果の解釈
・問題の設定と定式化の解説
・pythonで実装する方法の解説 ← 今回はここ!
の3つの記事に分かれています!
それでは解説していきましょう!
【Udemy講座公開のお知らせ】
このたびUdemyで数理最適化の講座を公開しました!この講座は「数理最適化を勉強してみたいけど数式が多くて難しい…」という方向けに、どうやって最適化問題を定式化すれば良いかを優しく丁寧に解説しています!
これまでのおさらい
今回の問題設定
今回の問題設定はこちらです。
今回考える問題
・あるアルバイトの1週間分のシフトを決める。(このシフトは1カ月使う)
・アルバイトの希望賃金との差がなるべく小さくなるようにシフトを作る
・アルバイト生は合計16人である。
・シフトの種類は日勤(d)、準夜勤(e)、深夜勤(n)の3つがある。
・各シフトの情報は以下の通りである。

詳しいことは下の記事で解説しています。
問題を数式で表す
今回の問題を数式で表すと下のようになります。
\(P=\{1,2,…,16\}\):アルバイト生\(i\)の集合
\(D=\{1,2,…,7\}\):曜日\(j\)の集合
\(S=\{d,e,n\}\):シフト\(k\)の集合
\(w_k \; (k \in S)\):シフト\(k\)の時給
\(np_k \; (k \in S)\) : シフト\(k\)での必要人数
\(e_i \; (i \in P)\):アルバイト生\(i\)の希望賃金
\(\text{min} \;\;\;\;\;\;t\)
\(\text{s.t.}\;\;\sum\limits_{j \in D,k \in S}8w_kx_{ijk}-e_i \leq t\;\;\;\;\; i \in P\)
\(\;\;\;\;\;\;\;e_i-\sum\limits_{j \in D,k \in S}8w_kx_{ijk} \leq t\;\;\;\;\; i \in P\)
\(\;\;\;\;\;\;\;\sum\limits_{i \in P}x_{ijk}=np_k\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\; j \in D,\; k \in S\)
\(\;\;\;\;\;\;\;\sum\limits_{k \in S}x_{ijk} \leq 1 \;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\; i \in P, \; j \in D\)
\(\;\;\;\;\;\;\;x_{ije}+x_{i(j+1)_{\text{mod}7}d} \leq 1\;\;\;\;\;\;\;\; i \in P,\; j \in D\)
\(\;\;\;\;\;\;\;x_{ijn}+x_{i(j+1)_{\text{mod}7}d} \leq 1\;\;\;\;\;\;\;\; i \in P,\; j \in D\)
\(\;\;\;\;\;\;\;x_{ijn}+x_{i(j+1)_{\text{mod}7}e} \leq 1\;\;\;\;\;\;\;\; i \in P,\; j \in D\)
\(\;\;\;\;\;\;\;\sum\limits_{j \in D,k \in S}x_{ijk} \leq 5 \;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\; i \in P\)
\(x_{ijn}+x_{i(j+1)_{\text{mod}7}n}+x_{i(j+2)_{\text{mod}7}n}+x_{i(j+3)_{\text{mod}7}n} \leq 3\;\;\;\;\;i \in P,\; j \in D\)
詳しいことは下の記事で解説しています。
今回はこの問題をpythonで解く方法を説明したいと思います!
最終的に出来上がったコード
最終的に出来上がったコードは以下のようになります。
## 事前準備
# pulpをインポート
! pip install pulp
from pulp import *
# numpyをインポート
import numpy as np
# ppprintをインポート
import pprint
# ランダムな値を固定する
np.random.seed(100)
# 集合の定義
P = {i for i in range(16)} # バイトの集合
D = {i for i in range(7)} # 曜日の集合
S = {"d", "e", "n"} # シフトの集合
# パラメータの定義
NumP = {"d":4, "e":3, "n":2} # 各シフトに必要な人数のパラメータ
E = dict(zip(P,np.random.randint(20000, 80000, 16))) # 各バイトの希望賃金のパラメータ
W ={"d":1000, "e":1200, "n":1500} # 各シフトの時給のパラメータ
# 変数の定義
x = pulp.LpVariable.dicts("x",(P,D,S), cat=LpBinary)
t = pulp.LpVariable("t", cat = LpContinuous)
## 問題の設定
# 問題を最小化に設定する
prob = LpProblem(sense=LpMinimize)
# 目的関数の設定
prob += t
# 制約条件の設定
# 目的関数を混合最適計画問題に表現したことによって生じた制約
for i in P:
prob += lpSum(8*W[k] * x[i][j][k] for j in D for k in S) - E[i] <= t
prob += E[i] - lpSum(8*W[k] * x[i][j][k] for j in D for k in S) <= t
# 各シフトの必要人数を満たす
for j in D:
for k in S:
prob += lpSum(x[i][j][k] for i in P) == NumP[k]
# 1日のシフトは1個まで
for i in P:
for j in D:
prob += lpSum(x[i][j][k] for k in S) <= 1
# 準夜勤→日勤を禁止
for i in P:
for j in D:
prob += x[i][j]["e"] + x[i][(j+1)%7]["d"] <= 1
# 夜勤→日勤を禁止
for i in P:
for j in D:
prob += x[i][j]["n"] + x[i][(j+1)%7]["d"] <= 1
# 夜勤→純夜勤を禁止
for i in P:
for j in D:
prob += x[i][j]["n"] + x[i][(j+1)%7]["e"] <= 1
# 勤務日数は最大5日まで
for i in P:
prob += lpSum(x[i][j][k] for j in D for k in S) <= 5
# 深夜勤は最大3連勤まで
for i in P:
for j in D:
prob += x[i][j]["n"] + x[i][(j+1)%7]["n"] + x[i][(j+2)%7]["n"] + x[i][(j+3)%7]["n"] <= 3
prob.solve() # 問題を解く
# 結果を表示
print(LpStatus[prob.status]) # 解の状態を表示(Optimalなら最適解が求められている)
print("Optimal Value =", value(prob.objective)) # 最適値を表示
# シフトを2次元リストで表す
data = [[] for i in range(len(P))]
for i in P:
for j in D:
if value(x[i][j]["d"]) == 1:
data[i].append("日")
elif value(x[i][j]["e"]) == 1:
data[i].append("準")
elif value(x[i][j]["n"]) == 1:
data[i].append("深")
else:
data[i].append("×")
pprint.pprint(data)これを実行すると以下のような結果が得られます。
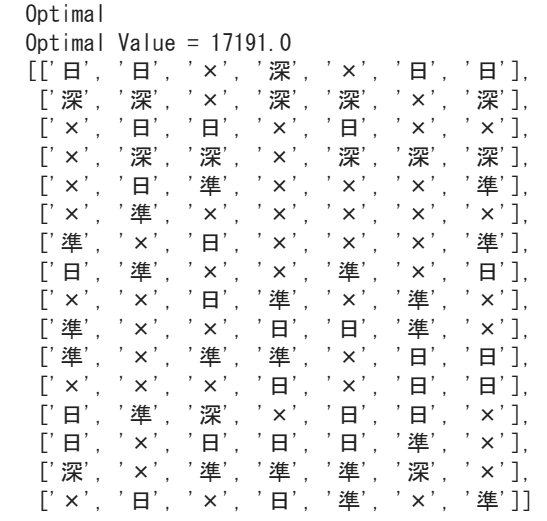
それでは1つずつ解説していきましょう!
事前準備
必要なものをインポートする
今回はpulpとnumpyとppprintを使ってコードを書いていこうと思います。pulpはpythonで数理最適化を扱うのに使います。numpyはランダムな数値を出力するときに使います。ppprintはリストを見やすく表示するために使います。
1~8行目でこれらをインポートしています。
## 事前準備
# pulpをインポート
! pip install pulp
from pulp import *
# numpyをインポート
import numpy as np
# ppprintをインポート
import pprintこれ以降numpyはnpと省略して書くことができます。
ランダムな値を固定する
後で話しますが、今回はアルバイト生の希望賃金をランダムで割り当てます。ところがとくに何も設定しないと実行するごとに希望賃金の値がランダムに変わってしまうので、「np.random.seed」を使って毎回同じ値が出力されるように固定します。
出力される値はランダムだけどその値が毎回固定されるという意味です。恣意的に値を選んでいるわけではありません。
10~11行目でランダムな値を固定しています。
# ランダムな値を固定する
np.random.seed(100)値の固定は「np.random.seed(数字)」でできます。数字の所に何を入れるかによってどんな数字に固定されるかが決まります。別に何でも良いんですけど今回は適当に100に設定しました。
文字の設定
まずはアルバイト生\(i\)の集合\(P\)、曜日\(j\)の集合\(D\)、シフト\(k\)の集合\(S\)を設定します。アルバイト生は\(P=\{1,2,…,16\}\)、曜日は\(D=\{1,2,…,7\}\)、シフトは\(S=\{d,e,n\}\)として設定します。
13~16行目でこれらを設定しています。今回は辞書形式で設定します。
# 集合の定義
P = {i for i in range(16)} # バイトの集合
D = {i for i in range(7)} # 曜日の集合
S = {"d", "e", "n"} # シフトの集合
次にパラメータの設定をします。イメージ的には集合の各要素ごとに設定されている値の集合みたいな感じです。例えば各シフトに必要な人数\(np_k\)はシフト\(k\)を代入するとそのシフトに必要な人数が返ってくるようなパラメータです。

pythonでは辞書という便利な機能があるのでそれを使って各種パラメータを表現したいと思います。17~20行目でパラメータを設定しています。
# パラメータの定義
NumP = {"d":4, "e":3, "n":2} # 各シフトに必要な人数のパラメータ
E = dict(zip(P,np.random.randint(20000, 80000, 16))) # 各バイトの希望賃金のパラメータ
W ={"d":1000, "e":1200, "n":1500} # 各シフトの時給のパラメータ辞書は{入力値1 : 出力値1, 入力値2 : 出力値2, …}で設定できます。NumPが各シフトの必要人数、Eが各バイト生の希望賃金、Wが各シフトの時給を表しています。例えばW[“d”]を実行したら1000が返ってきます。
「np.random.randint(20000,80000,16)」で20000円から80000円の間からランダムに整数を16個取り出しています。これを辞書形式にしたいので、「dict(zip())」を使ってアルバイト生の集合\(P\)と16個のランダムな整数の集合を辞書的に対応させています。
変数の設定
次に変数の設定をします。今回は\(x_{ijk}\)と\(t\)が変数になります。\(t\)は1個しかないので簡単に設定できますが、\(x_{ijk}\)は非常にたくさん設定する必要があります。
16×7×3 = 336個の変数\(x_{ijk}\)を作る必要があります。
# 変数の定義
x = pulp.LpVariable.dicts("x",(P,D,S), cat=LpBinary)
t = pulp.LpVariable("t", cat = LpContinuous)
変数は「pulp.LpVariable()」で設定できます。まず最初にtの説明からします。()の中にある”t”でこの変数にtという名前をつけています。cat = の所で変数の種類を設定します。tは任意の実数を取りうるので「LpContinuous」で連続値に設定しています。
次にxの説明をします。基本はtのときと一緒ですが、「pulp.Lpvariable」から「pulp.LpVariable.dicts()」に変えました。「.dicts()」を追加することによって(P,D,S)を添字の集合とする変数の設定ができます。この変数は0-1変数なので「cat = LpBinary」とします。
問題の設定
それではいよいよ問題の設定をしていきます。この部分は非常に長いので、問題の種類の設定、目的関数の設定、各制約条件の設定に分けて1つずつ説明していきます。
問題を最小化に設定
# 問題を最小化に設定する
prob = LpProblem(sense=LpMinimize)27~28行目で問題の最小化に設定しています。問題にはprobと名付けました。問題の設定は「LpProblem()」でできます。「sense=」の所で問題の最小化か最大化を設定できます。今回は最小化に設定したいので「LpMinimize」とします。
問題を最大化にしたいときは「sense = LpMaximize」とします。
目的関数の設定
# 目的関数の設定
prob += t30~31行目で目的関数を設定しています。これ以降目的関数や制約条件はprob+=から始めます。probはさっき問題に付けた名前です。目的関数は\(t\)なので「prob += t」とします。
制約条件の設定1:目的関数の変形によって生じた制約
# 目的関数を混合最適計画問題に表現したことによって生じた制約
for i in P:
prob += lpSum(8*W[k] * x[i][j][k] for j in D for k in S) - E[i] <= t
prob += E[i] - lpSum(8*W[k] * x[i][j][k] for j in D for k in S) <= t\(\sum\limits_{j \in D,k \in S}8w_kx_{ijk}-e_i \leq t\;\;\;\;\; i \in P\)
\(e_i-\sum\limits_{j \in D,k \in S}8w_kx_{ijk} \leq t\;\;\;\;\; i \in P\)
34~37行目でこの制約を設定しています。任意の\(i \in P\)に対して上の数式が成り立つ必要があります。pythonでは「for i in P」でループさせます。シグマは「lpSum()」で記述することができ、()の中身に足したいものを入れます。
「8*W[k] * x[i][j][k]」は\(8w_kx_{ijk}\)を表し、 「for j in D for k in S」がシグマの下の\(j \in D,k \in S\)を表しています。要はどの範囲で足し算するのかを設定しています。
制約条件の設定2:各シフトの必要人数を満たす
# 各シフトの必要人数を満たす
for j in D:
for k in S:
prob += lpSum(x[i][j][k] for i in P) == NumP[k]\(\sum\limits_{i \in P}x_{ijk}=np_k\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\; j \in D,\; k \in S\)
39~42行目でこの制約を設定しています。任意の曜日\(j\)とシフト\(k\)に対して、そのシフトでの必要人数\(np_k\)と実際にシフトに入る人数\(\sum\limits_{i \in P}x_{ijk}\)を一致させる必要があります。
制約条件の設定3:1日のシフトは1個まで
# 1日のシフトは1個まで
for i in P:
for j in D:
prob += lpSum(x[i][j][k] for k in S) <= 1\(\sum\limits_{k \in S}x_{ijk} \leq 1 \;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\; i \in P, \; j \in D\)
44~47行目でこの制約を設定しています。任意のバイト生\(i\)と曜日\(j\)に対して、1日に入るシフト数の合計\(\sum\limits_{k \in S}x_{ijk}\)が1以下になる必要があります。
制約条件の設定4:深夜勤→日勤、深夜勤→準夜勤、準夜勤→日勤は禁止
# 準夜勤→日勤を禁止
for i in P:
for j in D:
prob += x[i][j]["e"] + x[i][(j+1)%7]["d"] <= 1
# 夜勤→日勤を禁止
for i in P:
for j in D:
prob += x[i][j]["n"] + x[i][(j+1)%7]["d"] <= 1
# 夜勤→純夜勤を禁止
for i in P:
for j in D:
prob += x[i][j]["n"] + x[i][(j+1)%7]["e"] <= 1\(x_{ije}+x_{i(j+1)_{\text{mod}7}d} \leq 1\;\;\;\;\;\;\;\; i \in P,\; j \in D\)
\(x_{ijn}+x_{i(j+1)_{\text{mod}7}d} \leq 1\;\;\;\;\;\;\;\; i \in P,\; j \in D\)
\(x_{ijn}+x_{i(j+1)_{\text{mod}7}e} \leq 1\;\;\;\;\;\;\;\; i \in P,\; j \in D\)
49~62行目でこれらの制約を設定しています。\(j+1\)を7で割った余りをpythonで求めたい場合は(j+1)%7でできます。
制約条件の設定5:勤務日数は最大5日まで
# 勤務日数は最大5日まで
for i in P:
prob += lpSum(x[i][j][k] for j in D for k in S) <= 5\(\sum\limits_{j \in D,k \in S}x_{ijk} \leq 5 \;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\; i \in P\)
64~66行目でこの制約を設定しています。これまでとほぼ一緒なので説明は省略します。
制約条件の設定6:深夜勤は最大3連勤まで
# 深夜勤は最大3連勤まで
for i in P:
for j in D:
prob += x[i][j]["n"] + x[i][(j+1)%7]["n"] + x[i][(j+2)%7]["n"] + x[i][(j+3)%7]["n"] <= 3\(x_{ijn}+x_{i(j+1)_{\text{mod}7}n}+x_{i(j+2)_{\text{mod}7}n}+x_{i(j+3)_{\text{mod}7}n} \leq 3\;\;\;\;\;i \in P,\; j \in D\)
68~71行目でこの制約を設定しています。これまでとほぼ一緒なので説明は省略します。
問題を解いて結果を表示する
それでは最後に問題を解いて結果を表示する部分の説明をしていきます。この部分もいくつかのパートに分けて説明していきます。
問題を解く
prob.solve() # 問題を解く73行目で問題を解いています。問題を解きたい場合はさっき付けた名前の後ろに「.solve()」を付ければ解けます。(今回は「prob」と名付けたので「prob.solve()」で問題が解けます。)
結果を表示
# 結果を表示
print(LpStatus[prob.status]) # 解の状態を表示(Optimalなら最適解が求められている)
print("Optimal Value =", value(prob.objective)) # 最適値を表示75~77行目で答えがどうなっているかを出力しています。「LpStatus[prob.status]」で解の状態が分かります。「Optimal」と出力されたら最適解が求められています。
目的関数の値は「value(prob.objective)」で出力できます。

上の2行を見るとちゃんと最適解が求められていて、目的関数の値が17191であることが分かります。
シフトを2次元リスト形式で表示
# シフトを2次元リストで表す
data = [[] for i in range(len(P))]
for i in P:
for j in D:
if value(x[i][j]["d"]) == 1:
data[i].append("日")
elif value(x[i][j]["e"]) == 1:
data[i].append("準")
elif value(x[i][j]["n"]) == 1:
data[i].append("深")
else:
data[i].append("×")
pprint.pprint(data)79~91行目でシフトスケジュールのリストを出力しています。まず最初にrange(len(P))で16行の二次元空リストを作りdataに保管します。
1行目にはバイト生1、2行目にはバイト生2、…、16行目にはバイト生16のシフトに関する情報を入れます。また1列目には月曜日、2列目には火曜日、…、7列目には日曜日のシフトに関する情報を入れます。
\(x_{ijd}=1\):バイト生\(i\)の\(j\)曜日に”日”を追加(日勤)
\(x_{ije}=1\):バイト生\(i\)の\(j\)曜日に”準”を追加(準夜勤)
\(x_{ijn}=1\):バイト生\(i\)の\(j\)曜日に”深”を追加(深夜勤)
どれでもない:バイト生\(i\)の\(j\)曜日に”×”を追加(休み)
もし\(x_{ijd}=1\)ならリストに”日”を追加し、\(x_{ije}=1\)ならリストに”準”を追加し、\(x_{ijn}\)ならリストに”深”を追加し、どれも0なら”×”を追加します。“日”が日勤、“準”が準夜勤、“深”が深夜勤、“×”が休みを表しています。
全ての\(i \in P, \; j \in D\)に対してこの操作を実行したら最後にdataを表示します。2次元リストを表示するときにはpprintを使います。pprintはリストを見やすくするために使っています。
結果について考察している記事はこちらになります!
おわりに
いかがでしたでしょうか。
今回の記事ではシフト作成問題をpythonで実装する方法について解説していきました。
今後もこのような経営工学に関する記事を書いていきます!
最後までこの記事を読んでくれてありがとうございました。
普段は組合せ最適化の記事を書いてたりします。
ぜひ他の記事も読んでみてください!
このブログの簡単な紹介はこちらに書いてあります。
興味があったら見てみてください。
このブログでは経営工学を勉強している現役理系大学生が、経営工学に関することを色々話していきます!
ぼくが経営工学を勉強している中で感じたことや、興味深かったことを皆さんと共有出来たら良いなと思っています。
そもそも経営工学とは何なのでしょうか。Wikipediaによると
経営工学(けいえいこうがく、英: engineering management)は、人・材料・装置・情報・エネルギーを総合したシステムの設計・改善・確立に関する活動である。そのシステムから得られる結果を明示し、予測し、評価するために、工学的な分析・設計の原理・方法とともに、数学、物理および社会科学の専門知識と経験を利用する。
引用元 : 経営工学 – Wikipedia
長々と書いてありますが、要は経営、経済の課題を理系的な観点から解決する学問です。






初めまして!Pythonを使ってシフト表を作りたいと考え、ググってこのWebページにたどり着きました!
最初はExcelのVBAコードをネットで見つけたので、それをPythonコードに書き直そうと取り組みましたが、コードの可読性がやたらと低く、挫折しました。
そんな中、今回このページを見つけて、感激しました。何と言っても、シフト表を数式として展開する(目的函数、制約条件の設定)という手法に、このような素晴らしいものがあるのだと、60歳を間近にようやく知りました。
貴殿のブログは分かりやすく書かれていて素晴らしいです。これで勉強のとっかかり、さらには自分オリジナルのシフト表を作ってみたいと考えています。
さらに、一般的に整数最適化や経営工学に興味が出てきました。今後勉強して、応用できるような知識を身につけたいと考えております。まずは今回のような整数最適問題の参考書を教えていただけないでしょうか?
よろしくお願いいたします。
コメントありがとうございます!
数理最適化に登場する数式を理解したい場合は「しっかり学ぶ数理最適化 モデルからアルゴリズムまで 梅谷 俊治 (著)」が分かりやすいと思います。https://amzn.to/4nODl8Y
この本の第4章がまるまる整数計画問題を扱っています。(こちらは理論的な解説のみでプログラミングで実装する方法は書いておりません。)
pythonを使って数理最適化の問題を解きたい場合は「Pythonではじめる数理最適化(第2版): ケーススタディでモデリングのスキルを身につけよう岩永 二郎 (著), 石原 響太 (著), 西村 直樹 (著), 田中 一樹 (著)」が分かりやすいと思います。https://amzn.to/3GO5k7Z
残念ながらシフト作成は扱っていませんが、数理最適化問題をpythonで解くためのサンプルコードが非常に豊富に載っています。(こちらはプログラミングがメインで、数式の解説はあまり書いておりません。)