- 生産計画問題ってなに?
- 生産計画問題を線形計画問題として定式化したい…
- 生産計画問題をpythonで解きたい…
こんにちは!しゅんです!
今回の記事では生産計画問題を線形計画問題として定式化してpythonで解く方法を解説したいと思います!
それではやっていきましょう!
普段は組合せ最適化の記事を書いてたりします。
ぜひ他の記事も読んでみてください!
このブログの簡単な紹介はこちらに書いてあります。
興味があったら見てみてください。
このブログでは経営工学を勉強している現役理系大学生が、経営工学に関することを色々話していきます!
ぼくが経営工学を勉強している中で感じたことや、興味深かったことを皆さんと共有出来たら良いなと思っています。
そもそも経営工学とは何なのでしょうか。Wikipediaによると
経営工学(けいえいこうがく、英: engineering management)は、人・材料・装置・情報・エネルギーを総合したシステムの設計・改善・確立に関する活動である。そのシステムから得られる結果を明示し、予測し、評価するために、工学的な分析・設計の原理・方法とともに、数学、物理および社会科学の専門知識と経験を利用する。
引用元 : 経営工学 – Wikipedia
長々と書いてありますが、要は経営、経済の課題を理系的な観点から解決する学問です。
生産計画問題ってなに?
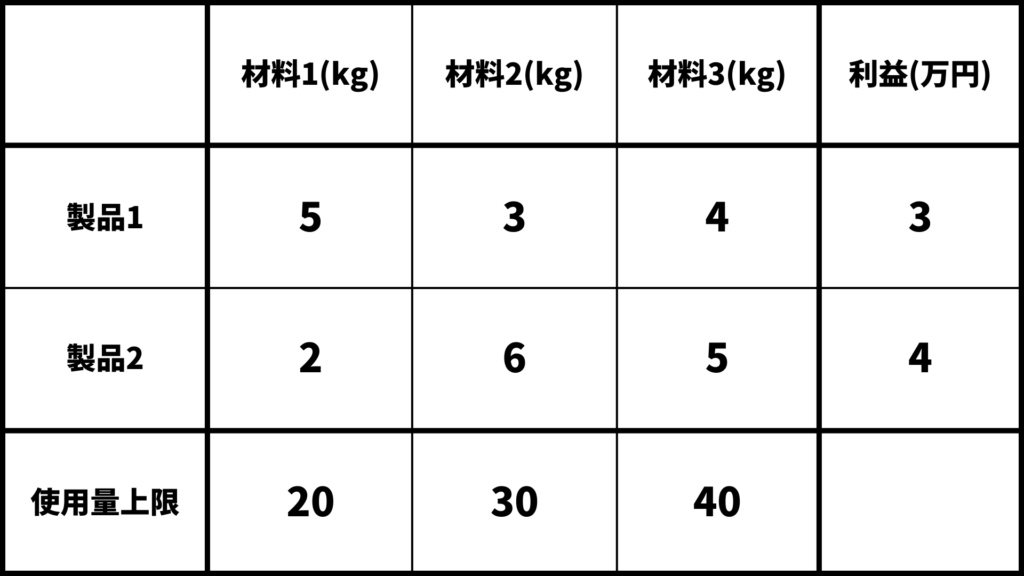
具体例を使って説明します。いま、3つの材料(材料1、材料2、材料3)を使って2つの製品(製品1、製品2)を生産することを考えます。
製品1を1kg作るためには材料1を5kg、材料2を3kg、材料3を4kg使います。
製品2を1kg作るためには材料1を2kg、材料2を6kg、材料3を5kg使います。
各材料の使用量上限はそれぞれ材料1が20kg、材料2が30kg、材料3が40kgで、この上限量を超えて材料を使用することはできません。
製品1を1kg売るときの利益は3万円で、製品2を1kg売るときの利益は4万円です。このような条件の下で、各製品をどれくらい生産すれば利益を最大化することができるでしょうか。
このような問題を生産計画問題と言います。
上記の制約の他にも例えば
・各材料の1kg当たりの費用
・各製品の生産にかかる時間と工場の稼働時間の上限
・各製品の生産量上限
など、様々な制約を考えることができます。
問題設定
今回は単純に「各材料の使用量上限」のみを考慮した生産計画問題について考えていきます。以下に問題設定を再掲します。

問題設定:
・3種類の材料を使って2種類の製品を生産することを考える。
・各製品を1kg生産するのに必要な材料量は一定で上の表の通りである。
・各材料の使用量上限が決まっており上の表の通りである。
・各製品を1kg販売したときの利益は一定で上の表のとおりである。
目的:
利益が最大となる各製品の生産量を決定する。
線形計画問題として定式化する
それでは次にこの生産計画問題を線形計画問題として定式化する方法を説明します。「記号の定義」、「目的関数の設定」、「制約条件の設定」の3つに分けてそれぞれ説明したいと思います。
記号の定義
パラメータ:
\(I\) : 製品の集合
\(J\) : 材料の集合
\(p_i\) : 製品\(i\)を1kg売るときの利益
\(q_{ij}\) : 製品\(i\)を1kg生産するのに必要な材料\(j\)の量
\(r_{j}\) : 材料\(j\)の使用量上限
変数:
\(x_{i}\) : 製品\(i\)の生産量
パラメータとして\(I,J,p,q,r\)を定義します。
\(I\)は製品の集合です。問題設定の例で言うと2種類の製品を生産するので
\(I = \{1,2\}\)
となります。\(J\)は材料の集合です。問題設定の例で言うと3種類の材料を使用するので
\(J = \{1,2,3\}\)
となります。\(p_{i}\)は製品\(i\)を1kg売るときの利益です。問題設定の例で言うと例えば製品1を1kg売るときの利益は3万円なので
\(p_{1}=3\)(万円は省略)
となります。\(q_{ij}\)は製品\(i\)を1kg生産するのに必要な材料\(j\)の量です。問題設定の例で言うと例えば製品2を1kg生産するのに必要な材料3の量は5kgなので
\(q_{23} = 5\)
となります。\(r_j\)は材料\(j\)の使用量上限です。問題設定の例で言うと例えば材料1の使用量上限は20kgなので
\(r_1 = 20\)
となります。
変数として\(x_i\)を定義します。\(x_i\)は製品\(i\)の生産量で、例えば製品1を1kg、製品2を3kg生産すると
\(x_1=1,x_2=3\)
となります。
変数\(x_i\)は連続変数です。
目的関数の設定
目的関数:
\(\sum\limits_{i \in I}p_{i}x_{i}\)
今回の生産計画問題の目的は
「利益が最大となる各製品の生産量を決定する」
というものです。
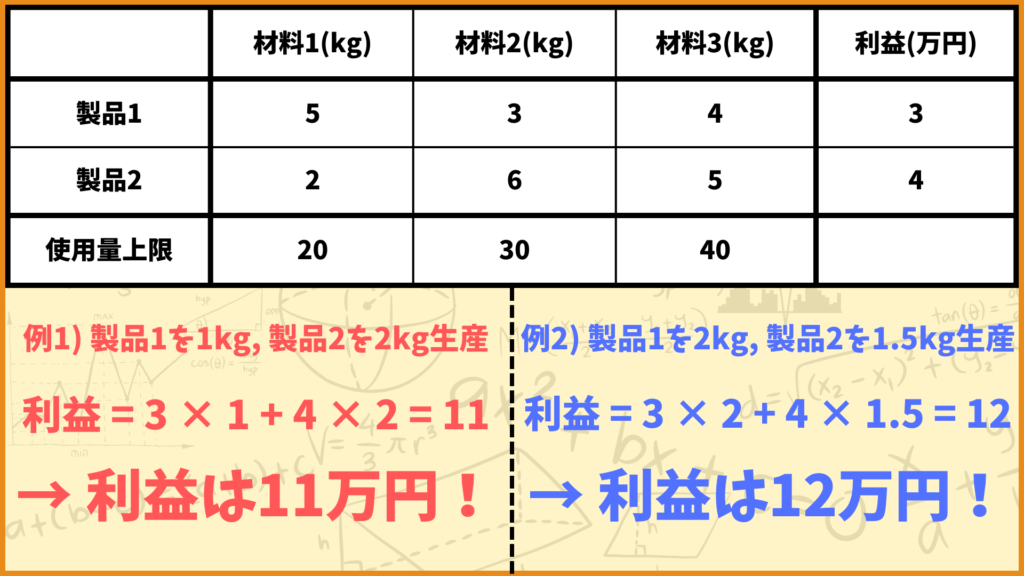
例えば上記の問題設定を考えます。製品1を1kg、製品2を2kg生産する場合の利益は
\(3 \times 1+4 \times 2=11\)
となります。このとき各変数の値は\(x_1=1,x_2=2\)となるので先ほど紹介した目的関数の値は
\(\sum\limits_{i \in I}p_{i}x_{i}=p_1x_1+p_2x_2=3\times 1+4\times 2=11\)
となり利益と一致します。他にも例えば製品1を2kg、製品2を1.5kg生産する場合の利益は
\(3 \times 2+4 \times 1.5=12\)
となります。このときの各変数の値は\(x_1=2,x_2=1.5\)となるので先ほど紹介した目的関数の値は
\(\sum\limits_{i \in I}p_{i}x_{i}=p_1x_1+p_2x_2=3\times 2+4\times 1.5=12\)
となり利益と一致します。
今回は利益が最大となる生産量を求めたいので、この目的関数を最大化する線形計画問題を作ります。
目的関数(最大化):
\(\sum\limits_{i \in I}p_{i}x_{i}\)
制約条件の設定
制約条件:
\(\sum\limits_{i \in I}q_{ij}x_{i} \leq r_{j} \;\; (\forall j \in J)\)
\(x_{i} \geq 0 \;\; (\forall i \in I)\)
1つずつ説明していきます。
1つ目の制約条件
1つ目の制約条件:
\(\sum\limits_{i \in I}q_{ij}x_{i} \leq r_{j} \;\; (\forall j \in J)\)
1つ目の制約条件は
「各材料の使用量は使用量上限を超えない」
ということを表しています。
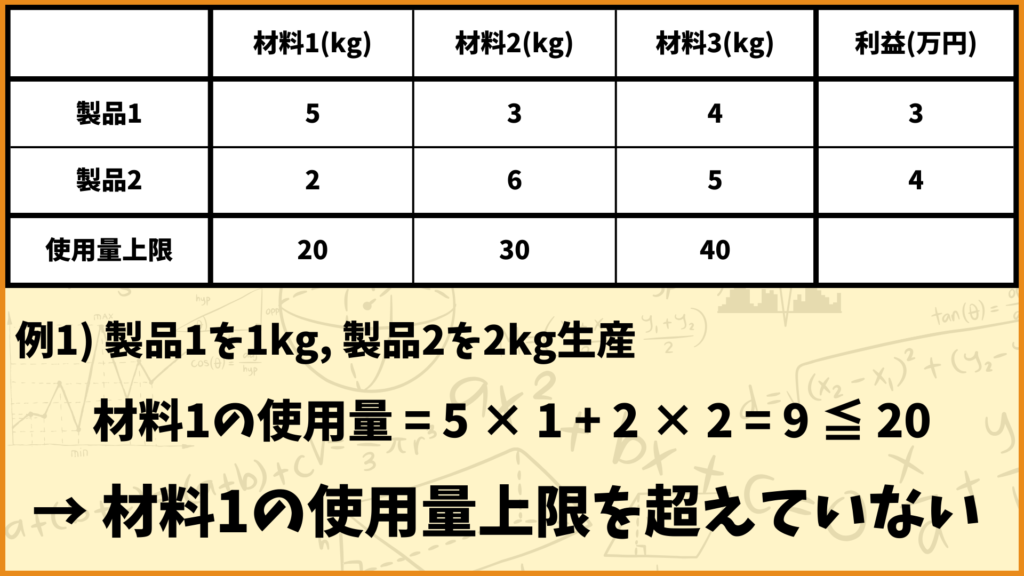
例えば製品1を1kg、製品2を2kg生産するときの材料1の使用量について考えてみましょう。このときの制約式の左辺は
\(\sum\limits_{i \in I}q_{i1}x_{i} = q_{11}x_{1}+q_{21}x_{2}=5\times 1+2\times 2=9\)
となりますが、これは材料1の使用量が9kgであるということを表しています。制約式の右辺は\(r_1 = 20\)なので制約式を満たしていますが、これは
「材料1の使用量が材料1の使用量上限を超えていない」
ということを表しています。
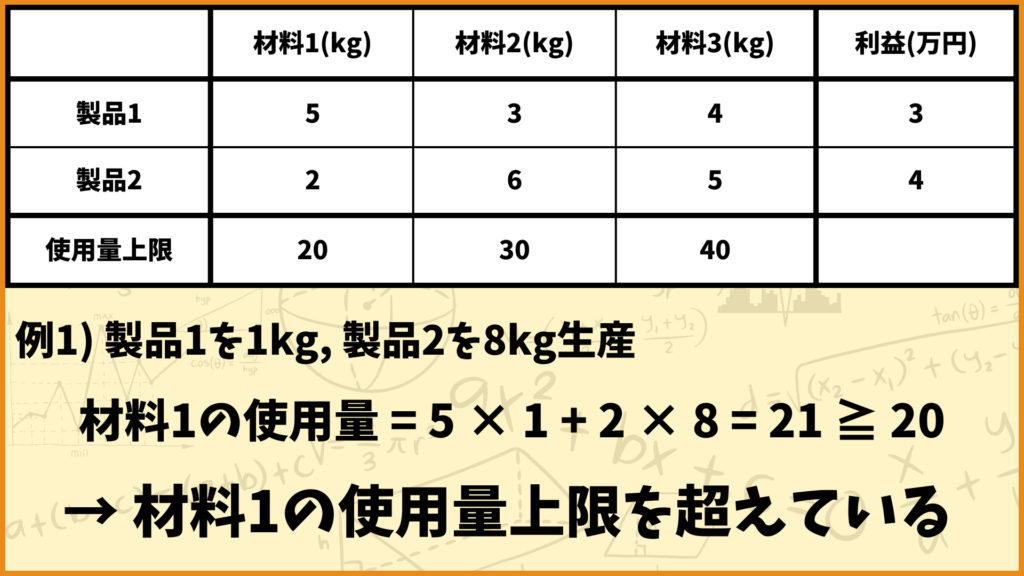
例えば製品1を1kg、製品2を8kg生産するときの材料1の使用量について考えてみましょう。このときの制約式の左辺は
\(\sum\limits_{i \in I}q_{i1}x_{i} = q_{11}x_{1}+q_{21}x_{2}=5\times 1+2\times 8=21\)
となりますが、これは材料1の使用量が21kgであるということを表しています。制約式の右辺は\(r_1 = 20\)なので制約式を満たしないですが、これは
「材料1の使用量が材料1の使用量上限を超えている」
ということを表しています。そのためこのように生産することはできません。
1つ目の制約条件:
\(\sum\limits_{i \in I}q_{ij}x_{i} \leq r_{j} \;\; (\forall j \in J)\)
2つ目の制約条件
2つ目の制約条件:
\(x_{i} \geq 0 \;\; (\forall i \in I)\)
2つ目の制約条件は
「各製品の生産量は0以上」
ということを表しています。これは特に説明しなくても理解できると思います。生産量がマイナスになると意味が分からなくなってしまいますね。
整数計画問題としてまとめる
以上のことを踏まえて整数計画問題として定式化しましょう。
パラメータ:
\(I\) : 製品の集合
\(J\) : 材料の集合
\(p_i\) : 製品\(i\)を1kg売るときの利益
\(q_{ij}\) : 製品\(i\)を1kg生産するのに必要な材料\(j\)の量
\(r_{j}\) : 材料\(j\)の使用量上限
変数:
\(x_{i}\) : 製品\(i\)の生産量
目的関数(最大化):
\(\sum\limits_{i \in I}p_{i}x_{i}\)
制約条件:
\(\sum\limits_{i \in I}q_{ij}x_{i} \leq r_{j} \;\; (\forall j \in J)\)
\(x_{i} \geq 0 \;\; (\forall i \in I)\)
ということで整数計画問題として定式化することができました。
pythonで解いてみた
それでは実際にこの問題をpythonで解いてみましょう。結論以下のプログラムを実行することで問題を解くことができます。
## 事前準備
import pulp # pulpをインポート
from pulp import LpMaximize, LpVariable, lpSum, LpStatus # pulpからLpMaximize, LpVariable, lpSum, LpStatusをインポート
## 記号の設定
I = [i for i in range(2)] # 製品の集合
J = [j for j in range(3)] # 材料の集合
p = [3,4] # 各製品を1kg売るときの利益
q = [[5,3,4],[2,6,5]] # 各製品を生産するのに必要な材料量
r = [20,30,40] # 材料の使用量上限
## 線形計画問題として定式化したものを解く
prob = pulp.LpProblem(sense = LpMaximize) # 問題を最大化に設定
x = LpVariable.dicts("x", I, cat="Continuous") # 変数を設定(連続変数に設定)
prob += lpSum(p[i] * x[i] for i in I) # 目的関数を設定
for j in J:
prob += lpSum(q[i][j] * x[i] for i in I) <= Q[j] # 1つ目の制約条件を設定
for i in I:
prob += x[i] >= 0 # 2つ目の制約条件を設定
result = prob.solve() # 問題を解く
## 結果の表示
print(f"解の状態 : {LpStatus[result]}") # 解の状態の表示
print(f"目的関数値 : {prob.objective.value()}") # 目的関数値の表示
for i in I:
print(f"x_{i+1} =", x[i].value()) # 変数の値を表示
このプログラムを実行したら上の結果が得られました。それではコードが何を表しているのか、そして得られた結果の見方について1つずつ解説していきます。
コードの解説
「事前準備」、「記号の設定」、「線形計画問題として定式化して解く」、「結果の表示」の4つに分けてそれぞれ解説していきます。
事前準備
## 事前準備
import pulp # pulpをインポート
from pulp import LpMaximize, LpVariable, lpSum, LpStatus # pulpからLpMaximize, LpVariable, lpSum, LpStatusをインポート
ここでは問題を解くために必要なものをインポートしています。pulpはpythonで線形計画問題を解くために使うライブラリで、そこからLpMaximize、LpVariable、lpSum、LpStatusをインポートしています。
LpMaximizeは最大化問題を扱うために使います。
LpVariableは変数を定義するために使います。
lpSumはシグマ記号\(\sum\)を扱うために使います。
LpStatusは解の状態を知るために使います。
記号の設定
## 記号の設定
I = [i for i in range(2)] # 製品の集合
J = [j for j in range(3)] # 材料の集合
p = [3,4] # 各製品を1kg売るときの利益
q = [[5,3,4],[2,6,5]] # 各製品を生産するのに必要な材料量
r = [20,30,40] # 材料の使用量上限
2行目で製品の集合\(I\)を設定しています。今回は製品の種類を2としました。
3行目で材料の集合\(J\)を設定しています。今回は材料の種類を3としました。
4行目で各製品を1kg売るときの利益\(p_i\)を設定しています。
5行目で各製品を生産するのに必要な材料量\(q_{ij}\)を設定しています。
6行目で材料の使用量上限\(r_j\)を設定しています。
線形計画問題として定式化して解く
## 線形計画問題として定式化したものを解く
prob = pulp.LpProblem(sense = LpMaximize) # 問題を最大化に設定
x = LpVariable.dicts("x", I, cat="Continuous") # 変数を設定(連続変数に設定)
prob += lpSum(p[i] * x[i] for i in I) # 目的関数を設定
for j in J:
prob += lpSum(q[i][j] * x[i] for i in I) <= Q[j] # 1つ目の制約条件を設定
for i in I:
prob += x[i] >= 0 # 2つ目の制約条件を設定
result = prob.solve() # 問題を解く
2行目で問題を最大化に設定しています。「sense = LpMinimize」だと目的関数を最小化する問題に設定できます。
4行目で変数を設定しています。「LpVariable.dicts()」は変数をいっぺんに設定できるので変数が多いときに便利です。括弧の中身は左から順に(”変数名”, 添字の集合, 変数の種類)となっています。
変数\(x_{i}\)の添字\(i\)は集合\(I\)中の要素なので「for i in I」とします。また「cat = “Continuous”」で変数を連続変数に設定しています。
6行目で目的関数
\(\sum\limits_{i \in I}p_{i}x_{i}\)
を設定しています。pulpで\(\sum\)は「lpSum」で表現できます。「x[i]」と書くことで\(x_{i}\)、「for i in I」と設定することで\(i \in I\)を表現できます。
8~9行目で1つ目の制約条件
\(\sum\limits_{i \in I}q_{ij}x_{i} \leq r_{j} \;\; (\forall j \in J)\)
11~12行目で2つ目の制約条件
\(x_{i} \geq 0 \;\; (\forall i \in I)\)
をそれぞれ設定しています。
14行目で問題を解いています。問題を解くときは「.solve()」でできます。
結果の表示
## 結果の表示
print(f"解の状態 : {LpStatus[result]}") # 解の状態の表示
print(f"目的関数値 : {prob.objective.value()}") # 目的関数値の表示
for i in I:
print(f"x_{i+1} =", x[i].value()) # 変数の値を表示
2行目で解の状態を表示しています。Optimalと表示されたら最適解が得られています。
3行目で最適解のときの目的関数値を表示しています。
4~5行目で最適解を表示しています。
pythonはリストのインデックスが0から始まるので、変数の値を表示するときに「x_{i+1}」としています。インデックスが0から始まることで計算自体に何か影響を及ぼすわけではなく別に「x_{i}」としても問題はないですが、これまでの説明と合わせるために「x_{i+1}」としています。
結果の解釈

上記のプログラムを実行したら上のような結果が得られました。1つずつ見ていきます。
1行目は解の状態を表しています。Optimalと表示されているので最適解が得られています。
2行目は最適解のときの目的関数値を表しています。今回の生産計画問題の利益の最大値は22.5万円であることが分かりました。
3~4行目は最適解を表しています。これを見ると利益を最大にするためには
製品1を2.5kg生産する
製品2を3.75kg生産する
上記のように製品を生産すれば良いことが分かりました。
材料の使用量上限を超えていないか確認する
今得られた最適解が本当に材料の使用量上限を超えていないかを確認してみます。以下のコードで確認してみましょう。
for j in J: # 全ての材料について調べる
sum = 0 # 各材料の使用量合計を求めるための初期値
for i in I:
sum += q[i][j]*x[i].value() # 各製品を生産するために使用した材料量をsumに加える
if sum <= r[j]: # 使用量上限を超えていない
print(f"材料{j+1}の使用量は{sum}で使用量上限の{r[j]}を超えていません。")
else: # 使用量上限を超えている
print(f"材料{j+1}の使用量は{sum}で使用量上限の{r[j]}を超えています。")
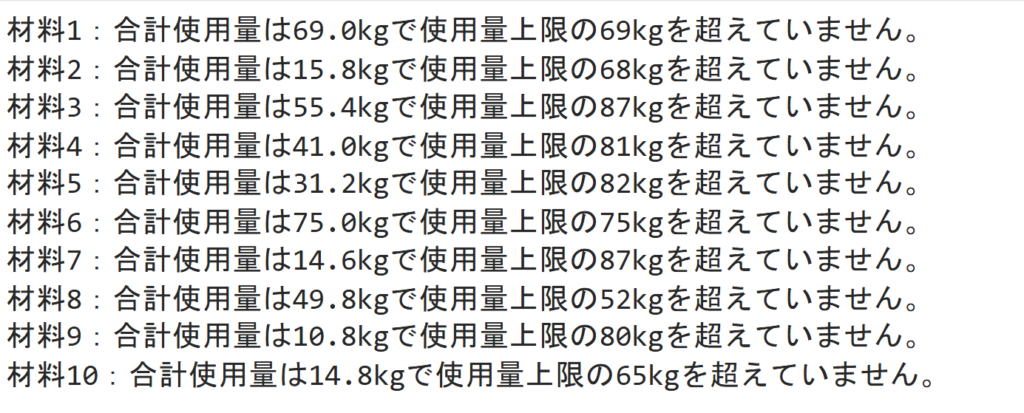
このコードは各材料の合計使用量を表示して、それが使用量上限を超えているか超えていないかを表示するコードです。表示を見るとちゃんとどの材料も使用量上限を超えていないことが分かります。
製品の種類と材料の種類を増やして計算してみる
それでは最後に製品の種類と材料の種類を増やして計算したときの結果を下に表示します。
製品数3、材料数10

計算結果


製品数5、材料数10
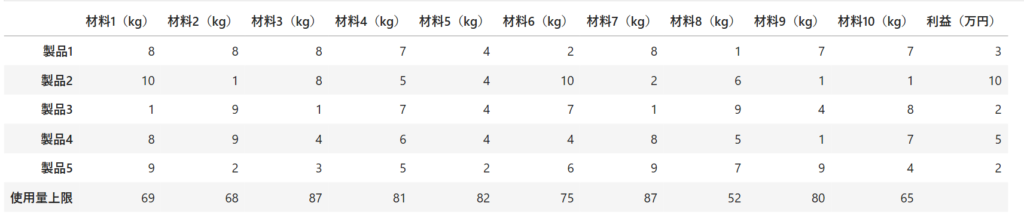
計算結果

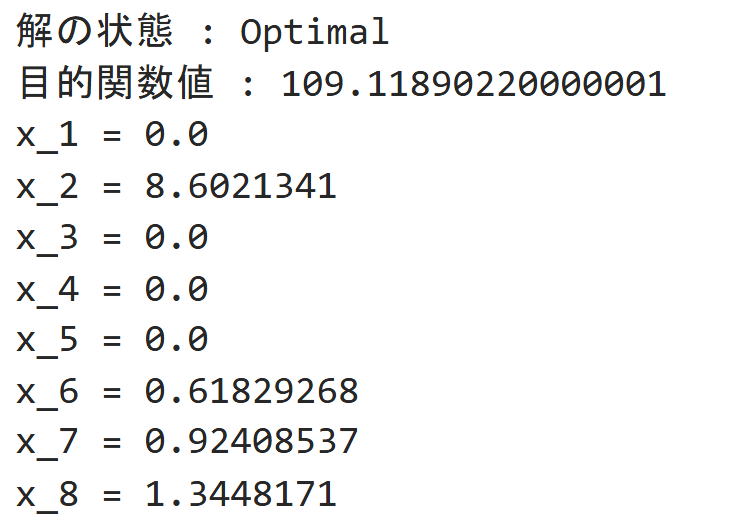
製品数8、材料数12
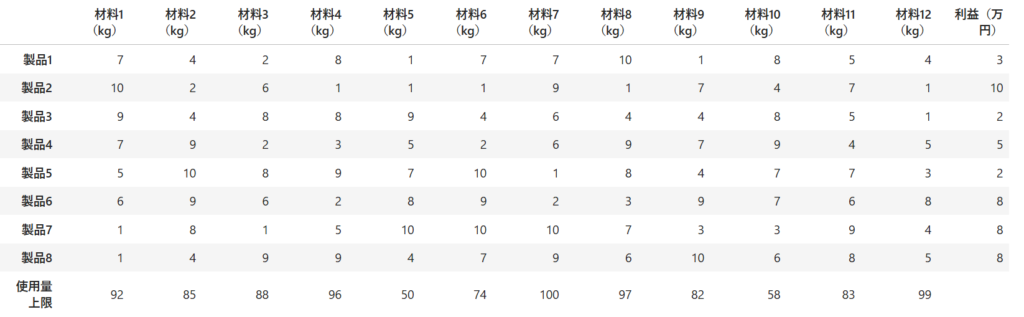
計算結果

おわりに
いかがでしたか。
今回の記事では生産計画問題について解説していきました。
今後もこのような組合せ最適化に関する記事を書いていきます!
最後までこの記事を読んでくれてありがとうございました。



