こんにちは!しゅんです!
この記事では集合被覆問題を使って現実の問題を解決する例を紹介しています。
それではやっていきましょう!
普段は組合せ最適化の記事を書いてたりします。
ぜひ他の記事も読んでみてください!
このブログの簡単な紹介はこちらに書いてあります。
興味があったら見てみてください。
このブログでは経営工学を勉強している現役理系大学生が、経営工学に関することを色々話していきます!
ぼくが経営工学を勉強している中で感じたことや、興味深かったことを皆さんと共有出来たら良いなと思っています。
そもそも経営工学とは何なのでしょうか。Wikipediaによると
経営工学(けいえいこうがく、英: engineering management)は、人・材料・装置・情報・エネルギーを総合したシステムの設計・改善・確立に関する活動である。そのシステムから得られる結果を明示し、予測し、評価するために、工学的な分析・設計の原理・方法とともに、数学、物理および社会科学の専門知識と経験を利用する。
引用元 : 経営工学 – Wikipedia
長々と書いてありますが、要は経営、経済の課題を理系的な観点から解決する学問です。
問題設定
まず最初に今回解きたい問題を設定しましょう。
ある都市に消防署を配置することを考える。ある都市はいくつかの区画に分かれている。消防署をある区画に配置すると、その区画から一定の距離までの区画をカバーする(つまりその区画で火事が起きたときに出動する)ことができる。いくつかの消防署を配置して全ての区画をカバーできるようにする。このとき、配置する消防署の数が最小になるような配置を求めたい。
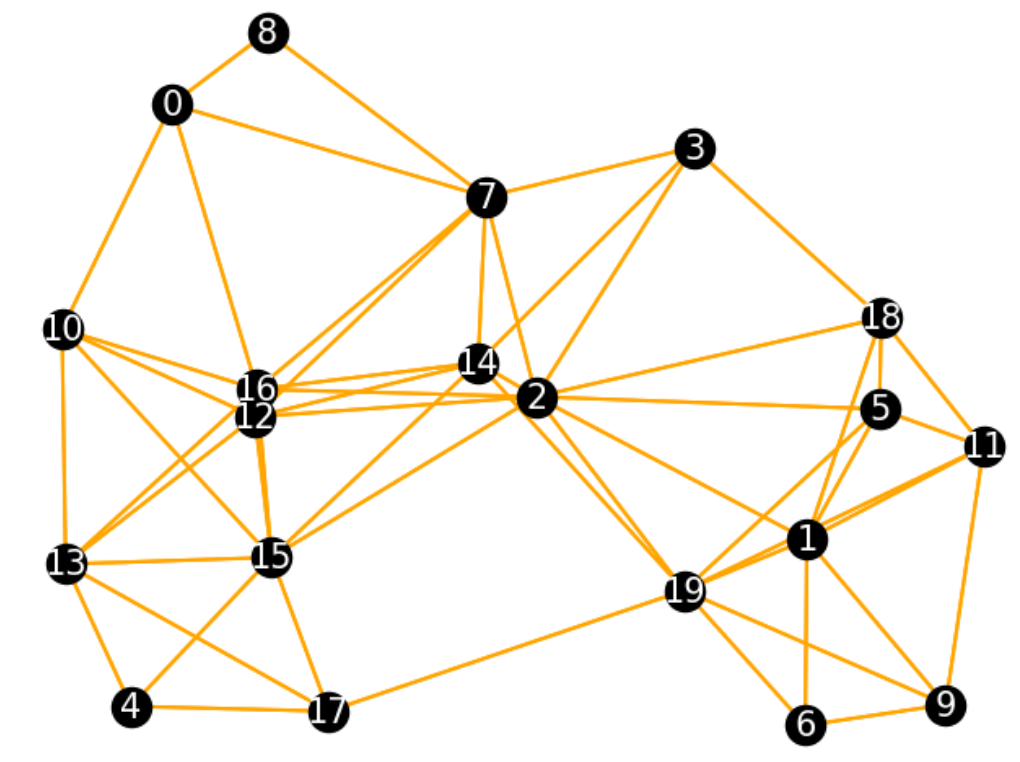
上図のような都市を考えてみます。各数字が区画を表しています。各辺はその辺の端点の区画間が一定の距離以下であることを表しています。つまりある区画に消防署を配置したとき、その区画に隣接する(辺で繋がっている)区画はその消防署でカバーできます。
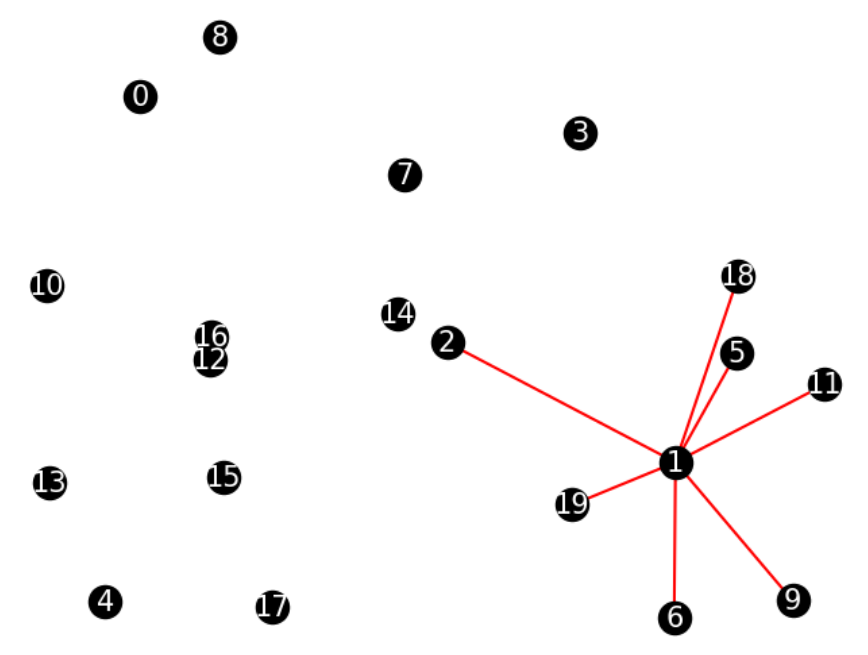
例えば区画1に消防署を配置することを考えます。このとき区画1に隣接する区画は2,5,6,7,11,18,19なので、この区画で発生した火事は区画1の消防署が対処できます。
全ての区画をカバーできている例
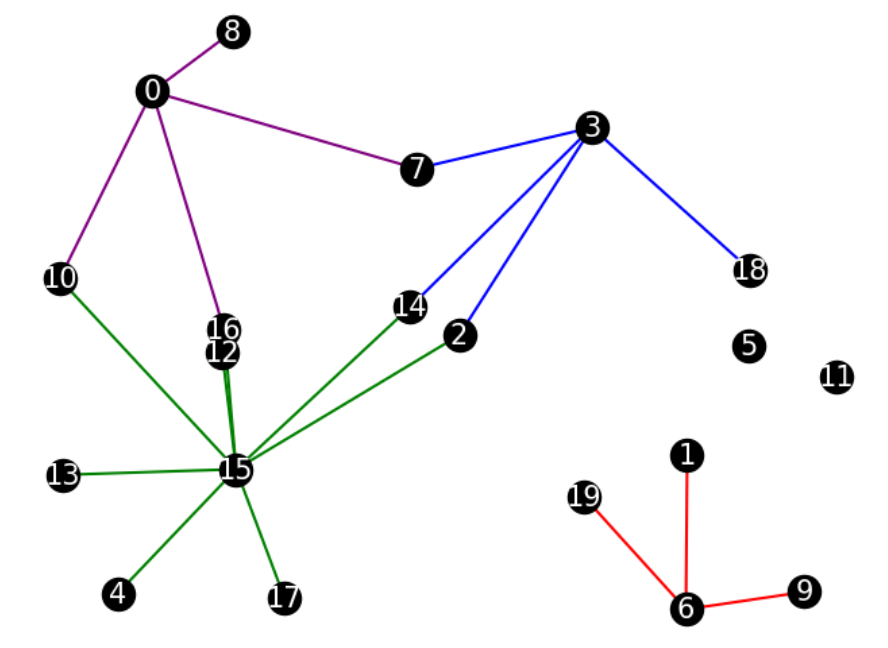
カバーできていない区画がある例
上の2つの図はどちらも消防署を4か所に配置した例です。左側は区画0,1,2,13に、右側は区画0,3,6,15にそれぞれ消防署を配置しています。
左側の例を見るとちゃんと全ての区画をカバーできていますね。ところが右側の例だと区画5と区画11をカバーすることができていません。これだと区画5,11で火事が起こった時に対処する消防署がないので今回の問題ではダメな例とします。
上の図は消防署を4か所に設置した例ですが、コスト削減のためにできることならなるべく少ない数の消防署で対処したいです。ということでこの記事では必要最小限な消防署の数を求めていきます。
消防署の配置問題と集合被覆問題
集合被覆問題ってなに?
今回の問題は集合被覆問題という問題に分類されます。
Wikipediaによると…
集合被覆問題(しゅうごうひふくもんだい)は、集合 U とその部分集合の族 S1,…,Sm が与えられたとき、U の要素を全てカバーするように部分集合の族から最小個数の部分集合を選ぶ問題。ここで、S1,…,Sm の和集合は、U に等しくなるものとする。
集合被覆問題 – Wikipedia
例えば\(U = \{1,2,3,4,5\}, S_1 = \{1,2\},S_2 = \{1,3,5\},S_3 = \{2,3,4\},S_4 = \{5\}\)とします。このとき\(S_2 \cup S_3 = U\)となり、1個の部分集合だけで\(U\)の要素をカバーすることはできないのでこの問題の答えは\(S_2,S_3\)となります。
消防署の配置問題は集合被覆問題とみなせる
今回考えている消防署の配置問題は集合被覆問題としてみなすことができます。\(U\)が全区画を要素に持つ集合、\(S_i\)が区画\(i\)に隣接する区画を要素とする集合とします。

上図で言うと例えば\(S_1 = \{2,5,6,9,11,18,19\}\)となります。

全ての区画をカバーできている例

カバーできていない区画がある例
また左側の例だと\(S_0 \cup S_1 \cup S_2 \cup S_{13} = U\)となるのでOKですが右側の例だと\(S_0 \cup S_1 \cup S_3 \cup S_{15} = U/\{5,11\}\)となるのでダメな例となります。
整数計画問題として定式化
それでは次に集合被覆問題を整数計画問題として定式化する方法を説明します。「記号の定義」、「目的関数の設定」、「制約条件の設定」の3つに分けてそれぞれ説明したいと思います。
記号の定義
パラメータ:
\(V\) : 区画の集合
\(E\) : 辺集合
変数:
\(x_{i} \in \{0,1\}\) : 区画\(i\)に消防署を設置するなら1、そうでないなら0を取る0-1変数
パラメータとして区画の集合\(V\)、辺集合\(E\)を設定します。辺\((i,j) \in E\)は区画\(i\)に消防署を置いたら区画\(j\)で火事が発生したときに出動できること(逆も然り)を表します。
変数\(x_{i}\)は区画\(i\)に消防署を設置するなら1、そうでないなら0を取る0-1変数を使います。例えば区画5に消防署を設置するなら\(x_5 = 1\)となります。
目的関数の設定
目的関数:
\(\sum\limits_{i \in V}x_i\)
今回の問題の目的は
「設置する消防署の数を最小化する」
というものです。

上の図でいうと
\(x_{0} = x_{1} = x_{2} = x_{13} = 1\)
となるので目的関数値は
\(\sum\limits_{i \in V}x_{i} = x_{0} + x_{1} + x_{2} + x_{13} = 4\)
となり、これは設置する消防署の数と対応していますね。今回はこれが最小となる場合を求めたいので問題を\(\text{minimize}\)に設定します。
目的関数を最小化:
\(\min \;\; \sum\limits_{i \in V}x_{i}\)
制約条件の設定
制約条件:
\(\sum\limits_{i \in V,(i,j) \in E}x_{i} \geq 1 \;\;\; (\forall j \in V)\)
制約条件は
「全ての区画をカバーする」
です。例えば区画3について考えてみましょう。

区画3に隣接する区画は2,7,14,18の4つです。区画3をカバーするためにはこの4つの区画、または区画3に少なくとも1つ消防署が設置されないといけません。そのため
\(x_{2} + x_{3} + x_{7} + x_{14} + x_{18} \geq 1\)
という不等式が成り立つ必要があります。
より一般的に考えてみましょう。区画\(j\)に隣接する区画を\(i\)とすると区画\(i\)は以下の条件を満たす必要があります。
\(i \in V, (i,j) \in E\)
これは\(i\)が区画の集合\(V\)中の要素で、かつ辺\((i,j)\)がE中の要素、つまり区画\(i,j\)が隣接していることを表します。ということで制約条件は上記のように表せます。
整数計画問題としてまとめる
以上のことを踏まえて整数計画問題として定式化しましょう。
パラメータ:
\(V\) : 区画の集合
\(E\) : 辺集合
変数:
\(x_{i} \in \{0,1\}\) : 区画\(i\)に消防署を設置するなら1、そうでないなら0を取る0-1変数
定式化:
\( \min \;\;\; \sum\limits_{i \in V}x_i\)
\(\;\text{s.t.}\;\;\;\sum\limits_{i \in V,(i,j) \in E}x_{i} \geq 1 \;\;\; (\forall j \in V)\)
\(\;\;\;\;\;\;\;\;\; x_{i} \in \{0,1\} \;\;\; (\forall i \in V)\)
ということで整数計画問題として定式化することができました。
pythonで解いてみた
それでは実際にこの問題をpythonで解いてみましょう。結論以下のプログラムを実行することで問題を解くことができます。
## 事前準備
from pulp import *
import random
import networkx as nx
import matplotlib.pyplot as plt## 記号の設定
random.seed(1) # ランダム値を固定
V = [i for i in range(20)] # 区画の集合を設定
# 各区画の座標を設定
Pos = {}
for i in V:
Pos[i] = (random.uniform(0,10),random.uniform(0,10)) # [0,10]×[0,10]の2次元ユークリッド平面上にランダムに設定
# 辺集合の設定
E = []
for i in V:
for j in V:
d = ((Pos[i][0] - Pos[j][0])**2 + (Pos[i][1] - Pos[j][1])**2)**(1/2) # 区画間の距離を計算
if d <= 4: # 長さが4以下の辺だけ採用
E.append((i,j))## 整数計画問題として定式化したものを解く
# 問題を最小化に設定
prob = pulp.LpProblem(sense = LpMinimize)
# 変数を設定
x = LpVariable.dicts("x", [i for i in V], cat="Binary")
# 目的関数を設定
prob += lpSum(x[i] for i in V)
# 制約条件を設定
for j in V:
prob += lpSum(x[i] for i in V if (i,j) in E) >= 1
# 問題を解く
result = prob.solve()## 結果の表示
# 解の状態を表示
print(LpStatus[result])
# 最適解の表示(値が1の変数だけ表示)
for i in V:
if x[i].value() == 1:
print(f"x_{i} =", x[i].value())
# 最適値の表示
print("最適値 :",prob.objective.value())
これらのプログラムを実行したら上の結果が得られました。それでは1つずつ説明していきます。
プログラムの説明
事前準備
## 事前準備
from pulp import *
import random
import networkx as nx
import matplotlib.pyplot as plt
問題を解くための事前準備としてpulp,random,networkx,matplotlibをインポートしましょう。pulpはpythonで数理計画問題を解くのに使います。randomはpythonでランダムを扱うときに使います。
networkxとmatplotlibはpythonでグラフを描画するのに使います。これら2つは問題を解くこと自体には必要ないですが結果を解釈するときに使います。
記号の設定
## 記号の設定
random.seed(1) # ランダム値を固定
V = [i for i in range(20)] # 区画の集合を設定
# 各区画の座標を設定
Pos = {}
for i in V:
Pos[i] = (random.uniform(0,10),random.uniform(0,10)) # [0,10]×[0,10]の2次元ユークリッド平面上にランダムに設定
# 辺集合の設定
E = []
for i in V:
for j in V:
d = ((Pos[i][0] - Pos[j][0])**2 + (Pos[i][1] - Pos[j][1])**2)**(1/2) # 区画間のユークリッド距離を計算
if d <= 4: # 距離の長さが4以下のものだけ採用
E.append((i,j))
次に記号の設定の所を説明します。
2行目ではランダム値を固定しています。こうしないと毎回各区画の座標が変わってしまいます。
3行目では区画の集合\(V\)を設定しています。とりあえず区画数は20にしました。
6~8行目で各区画の座標を設定しています。random.uniform(i,j)はi以上j以下の実数をランダムに1つ返す関数です。Posは辞書形式で各区画のx座標とy座標が格納されています。
10~15行目では辺を設定しています。13行目で各区画間のユークリッド距離を計算し、その距離が4以下のものだけ辺として採用しています。
これらのコードによって得られた区画の集合と辺集合をnetworkx,matplotlibを使って描画したのが以下のグラフです。(コードの説明は本題とは外れるので省略します。)

辺の長さ4以下
# グラフの初期化
G = nx.DiGraph()
# 頂点を追加
for v, pos in Pos.items():
G.add_node(v, pos=pos)
# グラフの描画
pos = nx.get_node_attributes(G, 'pos')
nx.draw(G, pos, with_labels=True, node_color='black', node_size=300,font_size = 15, font_color='white')
for (i,j) in E:
if i != j:
nx.draw_networkx_edges(G, pos, edgelist=[(i, j)], edge_color="orange", width=1.5, arrows=False)
ちなみに長さが3以下のものだけ辺として採用すると以下のようなグラフになり、当然このあとの計算結果も変わります。
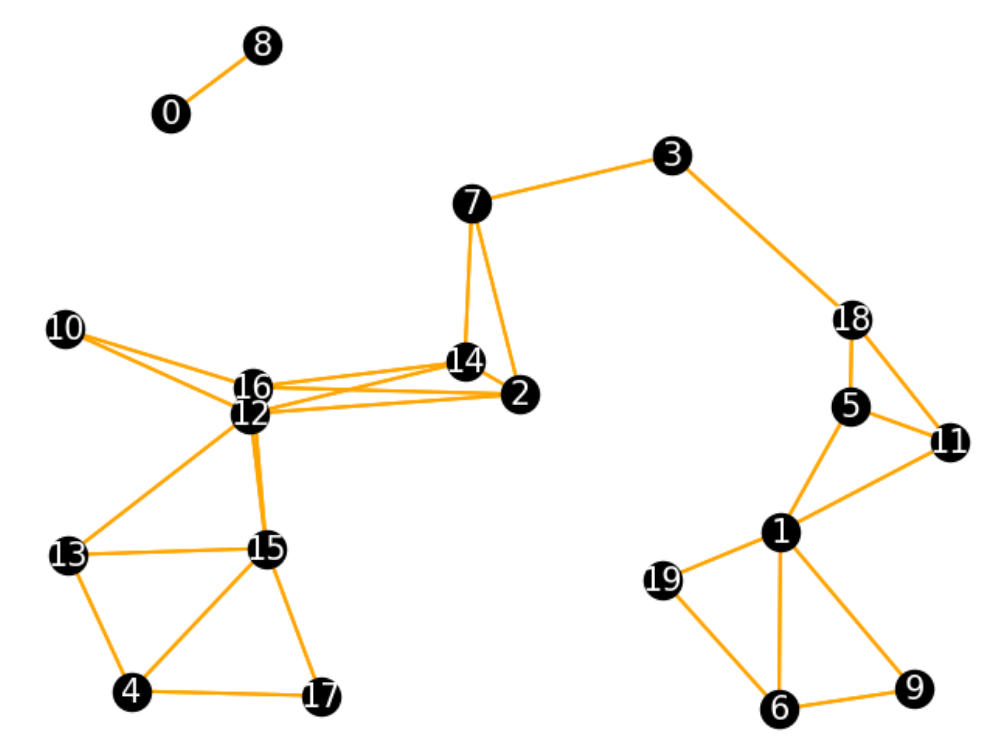
辺の長さ3以下
整数計画問題として定式化したものを解く
## 整数計画問題として定式化したものを解く
# 問題を最小化に設定
prob = pulp.LpProblem(sense = LpMinimize)
# 変数を設定
x = LpVariable.dicts("x", [i for i in V], cat="Binary")
# 目的関数を設定
prob += lpSum(x[i] for i in V)
# 制約条件を設定
for j in V:
prob += lpSum(x[i] for i in V if (i,j) in E) >= 1
# 問題を解く
result = prob.solve()
4行目で問題を最小化に設定しています。
7行目で0-1変数\(x_{i}\)の定義をしています。添字の\(i\)は区画\(i\)を表しているので[i for i in V]としています。0-1変数なので cat = “Binary”としています。
10行目で目的関数を設定しています。
12~13行目で制約条件を設定しています。
16行目で問題を解いています。
結果を表示する
## 結果の表示
# 解の状態を表示
print(LpStatus[result])
# 最適解の表示(値が1の変数だけ表示)
for i in V:
if x[i].value() == 1:
print(f"x_{i} =", x[i].value())
# 最適値の表示
print("最適値 :",prob.objective.value())
4行目で解の状態を表示します。Optimalと表示されたら最適解が得られています。
7~9行目で最適解を表示しています。
12行目で最適値を表示しています。
結果の解釈

1行目でOptimalと表示されているので最適解が得られていることが分かります。
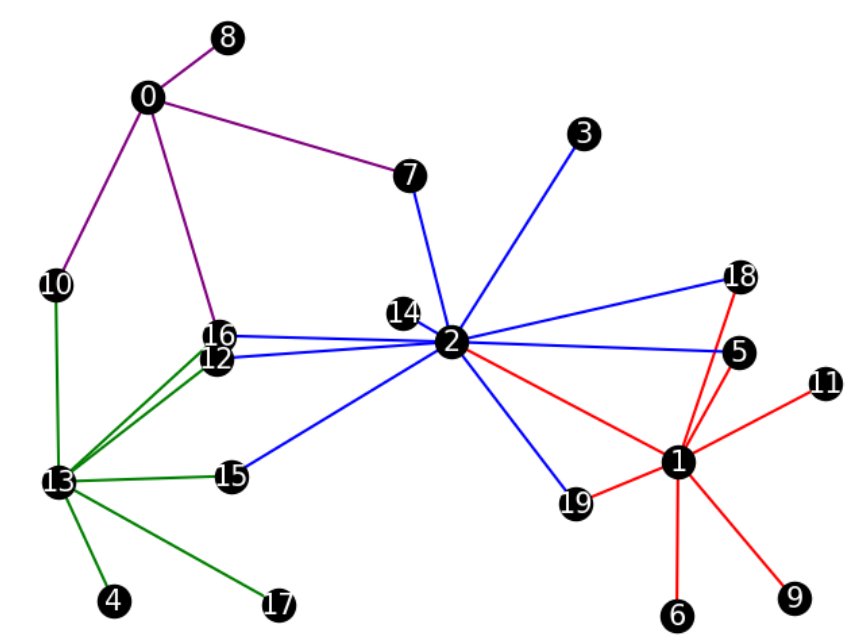
2~4行目では最適解を表示しています。これを見ると\(x_{1} = x_7 = x_{13} = 1\)であることが分かります。つまり区画1,7,13に消防署を設置することで全ての区画をカバーすることができ、かつ消防署の数を最小にすることができるという訳です。
文字だけじゃ分かりにくいのでグラフを描画して確認してみましょう。
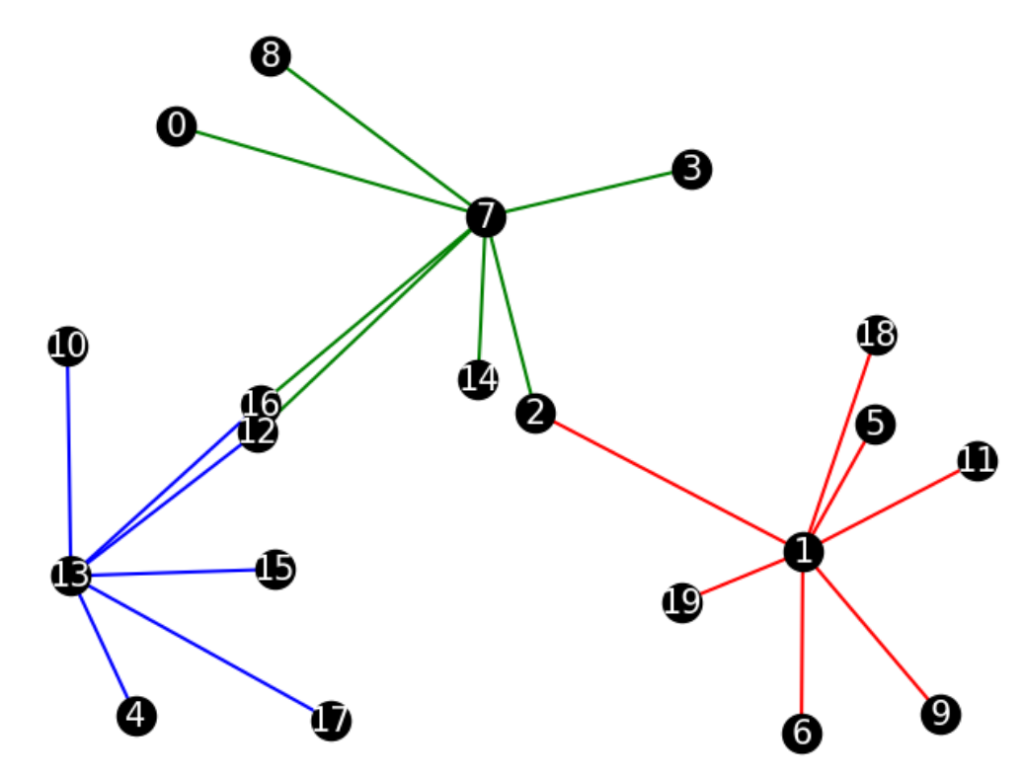
赤い辺が区画1に接続している辺、緑の辺が区画7に接続している辺、青い辺が区画13に接続している辺をそれぞれ表しています。これを見るとちゃんと全ての区画をカバーできていることが分かりますね。
## グラフを描画するコード
# グラフの初期化
G = nx.DiGraph()
# 頂点を追加
for v, pos in Pos.items():
G.add_node(v, pos=pos)
# グラフの描画
pos = nx.get_node_attributes(G, 'pos')
nx.draw(G, pos, with_labels=True, node_color='black', node_size=300,font_size = 15, font_color='white')
colors = ["r","g","b"]
count = 0
for i in V:
if x[i].value() == 1:
for j in V:
if (i,j) in E:
nx.draw_networkx_edges(G, pos, edgelist=[(i, j)], edge_color=colors[count], width=1.5, arrows=False)
count += 1 区画の数を増やしてみた
それでは最後に区画の数を100個に増やして計算してみましょう。コードはさっきとほぼ同じでパラメータの所だけいじってるだけなので省略します。消防署の数を増やしてみたいので長さが3以下のものだけグラフ中の辺として採用しています。

辺も描画すると多すぎてカオスになるので区画だけ表示しています。
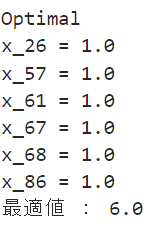
このグラフを入力したら上記のような結果が得られました。どうやら6個の消防署で全ての区画をカバーできるようです。これも文字だけじゃ分かりづらいのでグラフを描画して理解してみましょう。
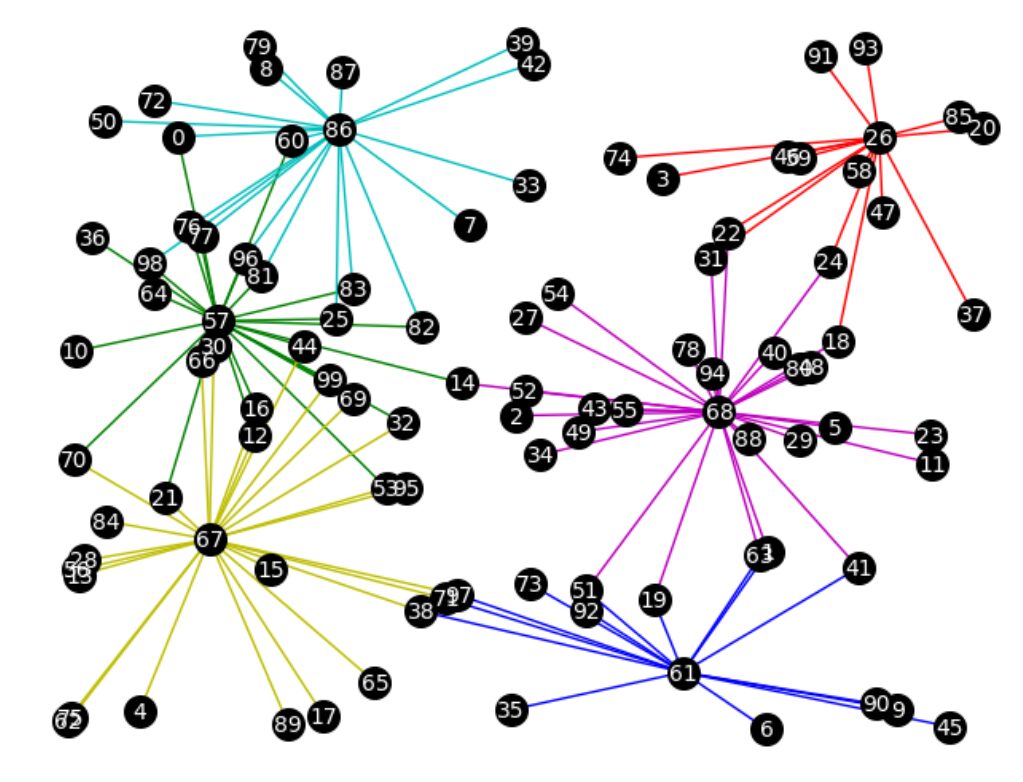
いい感じに消防署を配置できていますね。
おわりに
いかがでしたか。
今回の記事では集合被覆問題について解説していきました。
今後もこのような数理最適化に関する記事を書いていきます!
最後までこの記事を読んでくれてありがとうございました。



