こんにちは!しゅんです!
この記事ではダイクストラ法のアルゴリズムについて解説したいと思います!
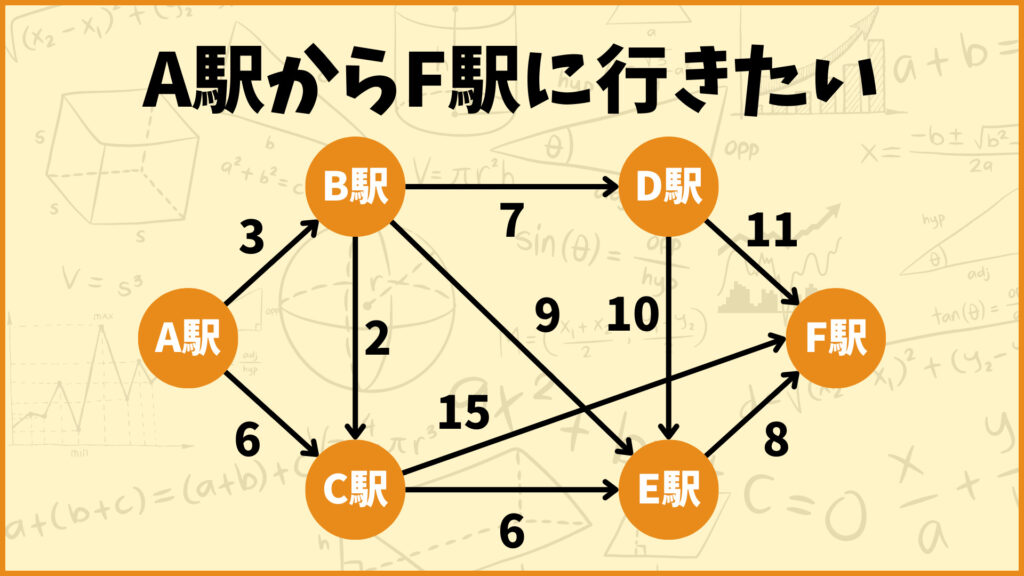
ダイクストラ法は最短経路問題を解くためのアルゴリズムです。最短経路問題とは、例えば電車でA駅からF駅に移動するときにどのルートで行けば一番早く着くかを求める問題です。
ということでこの記事では具体例を使ってダイクストラ法のアルゴリズムについて解説したいと思います!
普段は組合せ最適化の記事を書いてたりします。
ぜひ他の記事も読んでみてください!
このブログの簡単な紹介はこちらに書いてあります。
興味があったら見てみてください。
このブログでは経営工学を勉強している現役理系大学生が、経営工学に関することを色々話していきます!
ぼくが経営工学を勉強している中で感じたことや、興味深かったことを皆さんと共有出来たら良いなと思っています。
そもそも経営工学とは何なのでしょうか。Wikipediaによると
経営工学(けいえいこうがく、英: engineering management)は、人・材料・装置・情報・エネルギーを総合したシステムの設計・改善・確立に関する活動である。そのシステムから得られる結果を明示し、予測し、評価するために、工学的な分析・設計の原理・方法とともに、数学、物理および社会科学の専門知識と経験を利用する。
引用元 : 経営工学 – Wikipedia
長々と書いてありますが、要は経営、経済の課題を理系的な観点から解決する学問です。
今回解く問題

今回は上図の問題を解いてみたいと思います。今A駅からF駅に行きたいとします。F駅に行くために、今回はB~E駅を経由して向かうことを考えます。
ある駅からどの駅に直接行けるかは駅の間の矢印で表しています。例えばA駅からB駅に向かって矢印が伸びていますが、これはA駅から直接B駅へ到達できることを表しています。逆にA駅からD駅へ矢印は伸びていませんが、これはA駅から直接D駅には行けないということを表しています。
ある駅から別の駅に行くまでにかかる時間はその駅間の矢印の上に書いてある数字で表しています。例えばA駅からB駅に向かう矢印の上には3と書いてありますが、これはA駅からB駅に行くまで3分かかるということを表しています。
問題を簡単にするため今回は乗りかえや電車の待ち時間などは全て0分とし、単純に電車に乗っている時間だけを考えたいと思います。
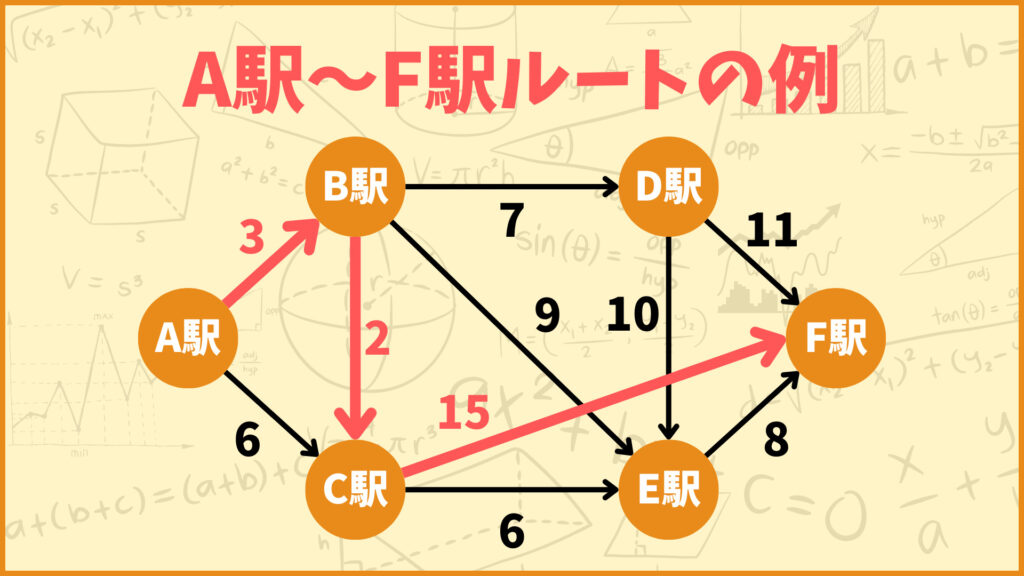
例えば上の図はA駅からB駅とC駅を経由してF駅に向かうルートを表しています。このルートで行く場合、移動にかかる時間は\(3+2+15 = 20\)分となります。
他にもルートはたくさん存在しており、どのルートで行くかによって移動時間は全然違います。ということで今回は、最短時間でA駅からF駅へ行けるルートを探すという問題を解きたいと思います。
ダイクストラ法ってなに?
ダイクストラ法の手順は以下の通りです。(とはいえ文字で説明されても理解するのが難しいと思うので、第4章では上の具体例を使って説明しています。)
入力:有向グラフ\(G = (V,E)\)と辺の重み\(w\)と始点\(s\)と終点\(t\)
目的;始点\(s\)から終点\(t\)までの最短距離
STEP.0 :
\(S = \emptyset, T = V\)とする。また\(d(i)\)を「その時点での始点\(s\)から頂点\(i\)までの最短距離」とする。(STEP.0では\(d(s)=0\)、\(s\)以外の頂点\(i\)は\(d(i)= \infty\))
STEP.1 :
頂点\(i \in T\)の中で\(d(i)\)が一番小さい頂点を選ぶ。その頂点に隣接する頂点\(j\)の\(d(j)\)を以下のように更新する。
\(d(j) \gets \min\{d(j), d(i) + w(i,j)\}\)
\(S\)に\(i\)を加え、\(T\)から\(i\)を取り除く。
STEP.2 :
頂点\(i \in T\)の中で\(d(i)\)が一番小さい頂点を選ぶ。その頂点に隣接する頂点\(j\)の\(d(j)\)を以下のように更新する。
\(d(j) \gets \min\{d(j), d(i) + w(i,j)\}\)
\(S\)に\(i\)を加え、\(T\)から\(i\)を取り除く。
・
・ \(T = \emptyset\)となるまで繰り返す。
・
\(d(t)\)を返す。
文字だけ見ても分かりづらいので実際に問題を解きながら説明していきます。
ダイクストラ法を使って問題を解いてみる

それでは実際に上の問題を解いていきましょう。有向グラフ\(G=(V,E)\)は上の図のことを表しています。なお、\(V\)は頂点集合なので\(V = \{A,B,C,D,E,F\}\)とします。また辺の重みは矢印の上に書いてある数字で表していて、始点は\(A\)、終点は\(F\)です。
STEP. 0
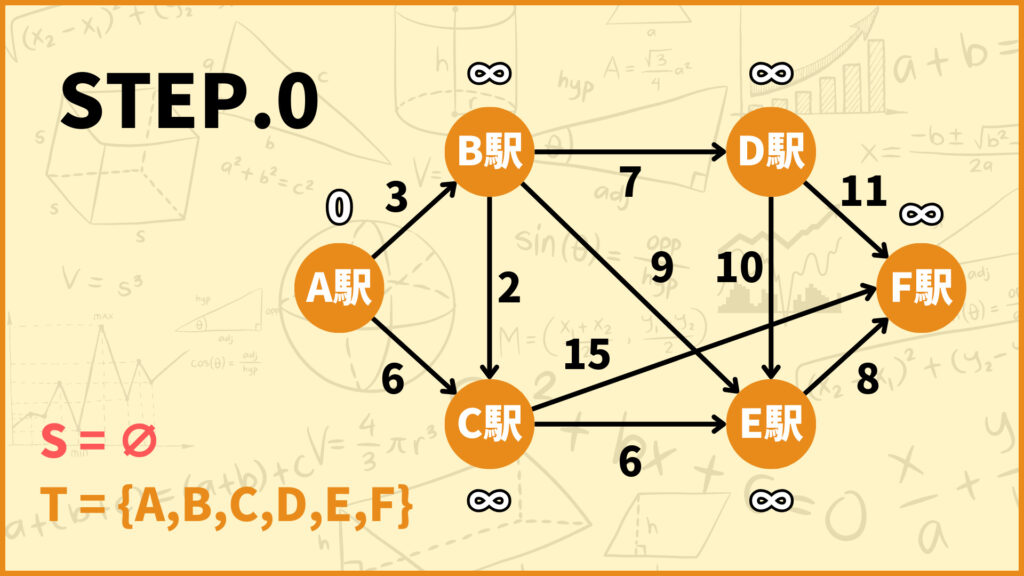
それではまずSTEP.0の説明をします。\(S= \emptyset, T = V =\{A,B,C,D,E,F\}\)とします。各頂点の上に書いてある数字が\(d(i)\)です。始点のA駅だけ0であとは\(\infty\)とします。
STEP. 1
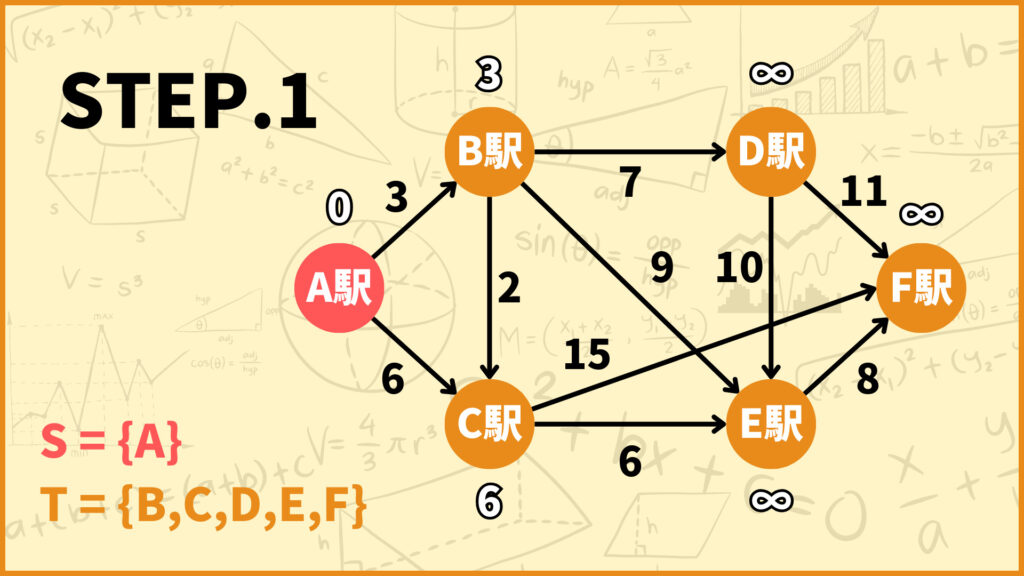
STEP.0で\(T=\{A,B,C,D,E,F\}\)としました。\(T\)中の頂点で\(d(i)\)が最も小さいのは始点\(A\)です。
\(A\)に隣接する頂点は\(B,C\)なので、\(d(B),d(C)\)を更新しましょう。
頂点\(B\) : \(d(B) \gets \min\{\infty, 0 + 3\} = 3\)
頂点\(C\) : \(d(C) \gets \min\{\infty, 0 + 6\} = 6\)
そして\(S\)に\(A\)を加えて\(T\)から\(A\)を取り除きましょう。
\(S = \{A\}\)
\(T = \{B,C,D,E,F\}\)
STEP. 2
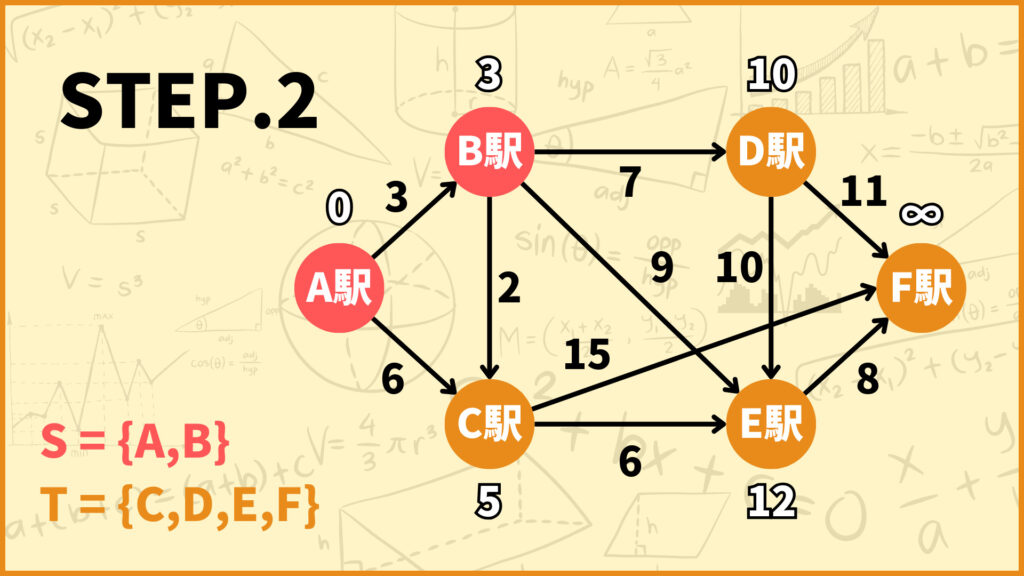
STEP.1で\(T=\{B,C,D,E,F\}\)としました。\(T\)中の頂点で\(d(i)\)が最も小さいのは始点\(B\)です。\((d(B)=3)\)
\(B\)に隣接する頂点は\(C,D,E\)なので、\(d(C),d(D),d(E)\)を更新しましょう。
頂点\(C\) : \(d(C) \gets \min\{6, 3 + 2\} = 5\)
頂点\(D\) : \(d(D) \gets \min\{\infty, 3 + 7\} = 10\)
頂点\(E\) : \(d(E) \gets \min\{\infty, 3 + 9\} = 12\)
そして\(S\)に\(B\)を加えて\(T\)から\(B\)を取り除きましょう。
\(S = \{A,B\}\)
\(T = \{C,D,E,F\}\)
\(d(C)\)が6から5に更新されましたがこれは
「A駅から直接C駅に行くと6分かかるが、A駅からB駅を経由してC駅に行くと5分で行ける」
ということを表しています。
STEP. 3
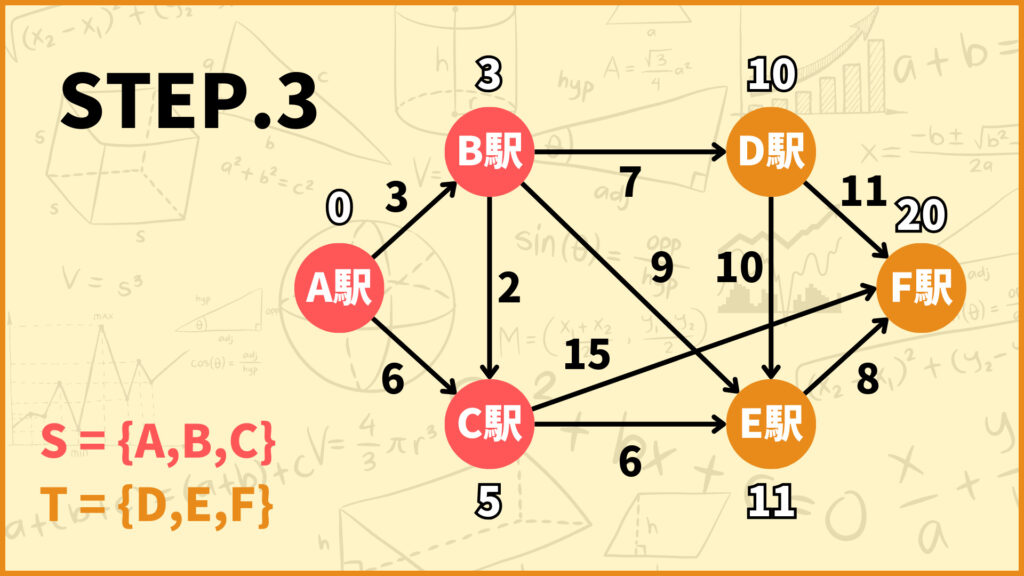
STEP.2で\(T=\{C,D,E,F\}\)としました。\(T\)中の頂点で\(d(i)\)が最も小さいのは始点\(C\)です。\((d(C)=5)\)
\(C\)に隣接する頂点は\(E,F\)なので、\(d(E),d(F)\)を更新しましょう。
頂点\(E\) : \(d(E) \gets \min\{12, 5 + 6\} = 11\)
頂点\(F\) : \(d(F) \gets \min\{\infty, 5 + 15\} = 20\)
そして\(S\)に\(C\)を加えて\(T\)から\(C\)を取り除きましょう。
\(S = \{A,B,C\}\)
\(T = \{D,E,F\}\)
\(d(E)\)が12から11に更新されましたがこれは
「A駅からB駅を経由してE駅に行くと12分かかるが、A駅からB駅とC駅を経由してE駅に行くと11分で行ける」
ということを表しています。
STEP. 4
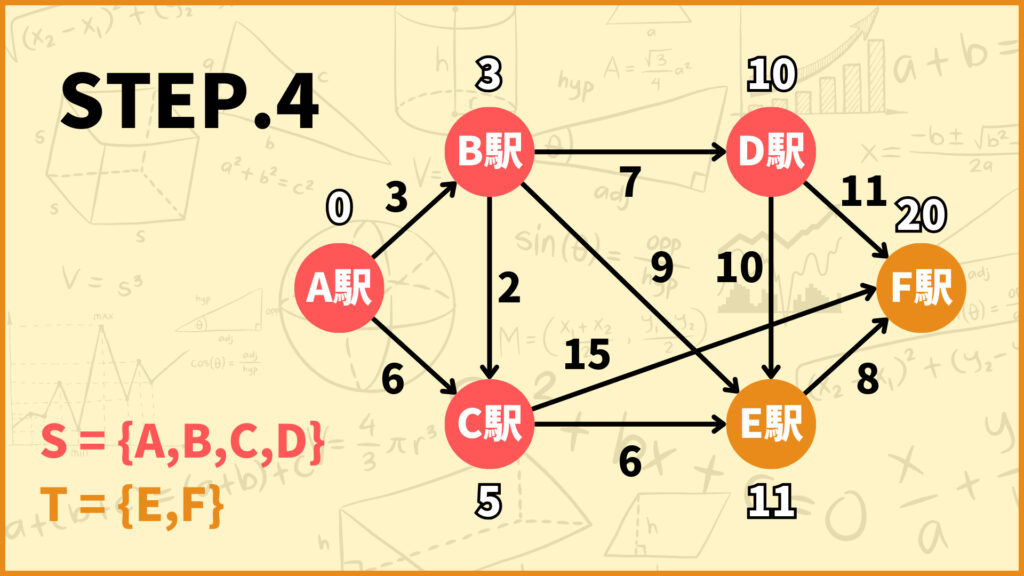
STEP.3で\(T=\{D,E,F\}\)としました。\(T\)中の頂点で\(d(i)\)が最も小さいのは始点\(D\)です。\((d(D)=10)\)
\(D\)に隣接する頂点は\(E,F\)なので、\(d(E),d(F)\)を更新しましょう。
頂点\(E\) : \(d(E) \gets \min\{11, 10 + 10\} = 11\)
頂点\(F\) : \(d(F) \gets \min\{20, 10 + 11\} = 20\)
そして\(S\)に\(D\)を加えて\(T\)から\(D\)を取り除きましょう。
\(S = \{A,B,C,D\}\)
\(T = \{E,F\}\)
\(d(E)\)も\(d(F)\)も更新されませんでしたが、これはD駅を経由するルートは遅い(D駅経由のルートよりももっと早く行けるルートが既に見つかっている)と言うことを表していますね。
STEP. 5
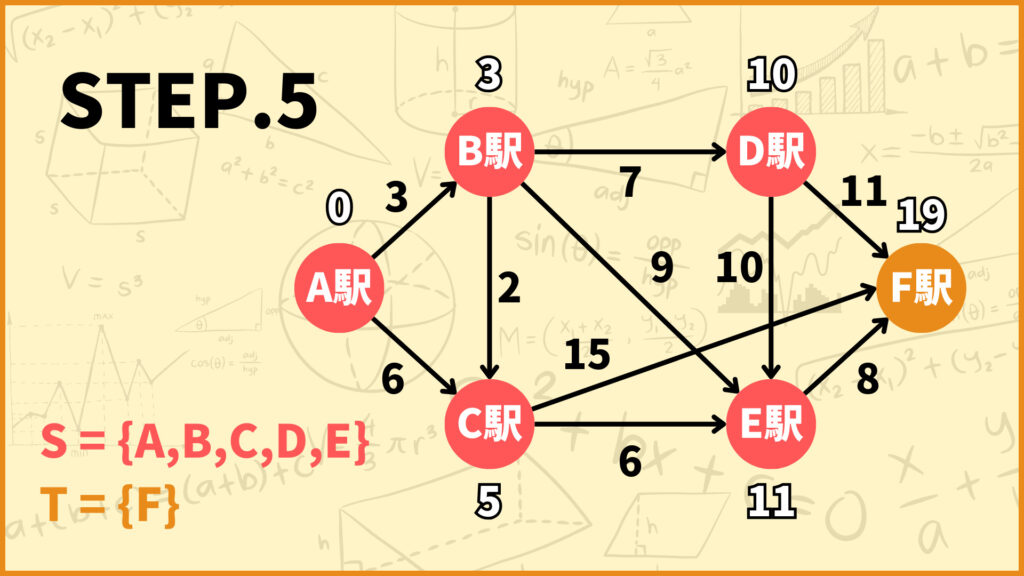
STEP.4で\(T=\{E,F\}\)としました。\(T\)中の頂点で\(d(i)\)が最も小さいのは始点\(E\)です。\((d(E)=11)\)
\(E\)に隣接する頂点は\(F\)なので、\(d(F)\)を更新しましょう。
頂点\(F\) : \(d(F) \gets \min\{20, 11 + 8\} = 19\)
そして\(S\)に\(E\)を加えて\(T\)から\(E\)を取り除きましょう。
\(S = \{A,B,C,D,E\}\)
\(T = \{F\}\)
\(d(E)\)が20から19に更新されましたがこれは
「A駅→B駅→C駅→F駅の順で行くと20分かかるが、A駅→B駅→C駅→E駅→F駅で行くと19分で行ける」
ということを表しています。
STEP. 6
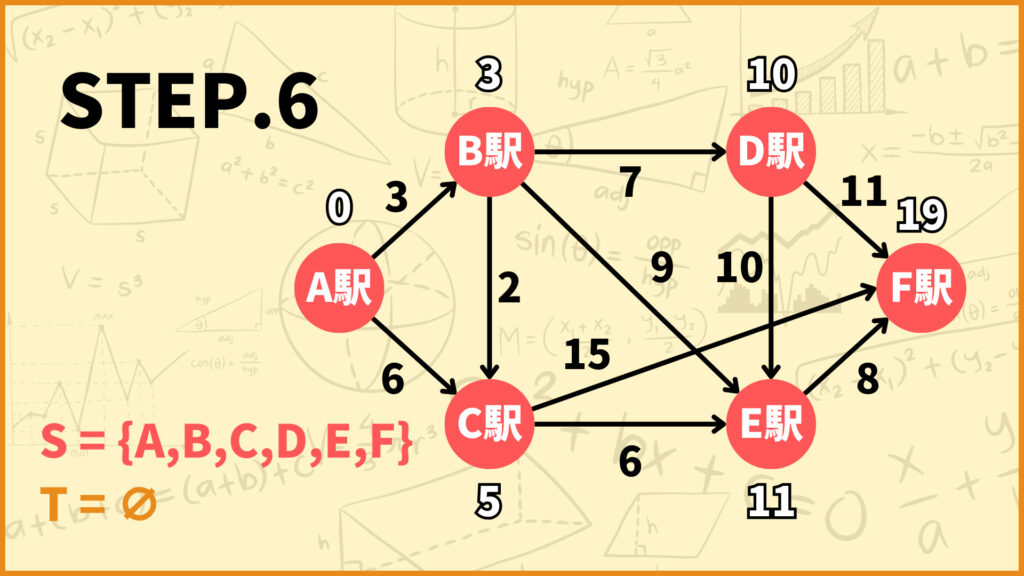
STEP.5で\(T=\{F\}\)としました。\(T\)中の頂点で\(d(i)\)が最も小さいのは始点\(F\)です。\((d(F)=19)\)
\(F\)に隣接する頂点は存在しないのでこのSTEPでは何もしません。
\(d(F)\)を返す
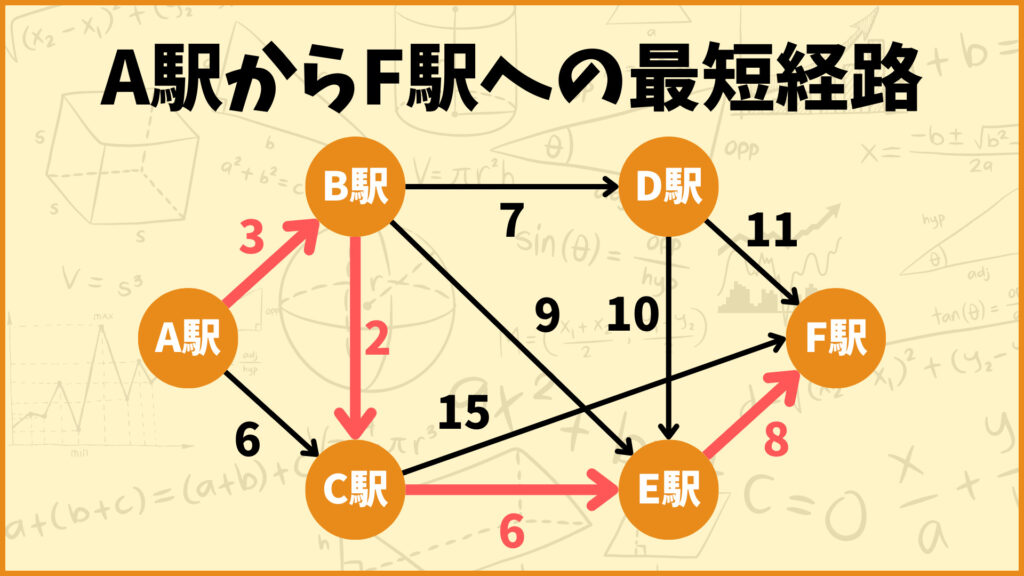
ということで\(T = \emptyset\)となったので、終点\(F\)の\(d(F)\)を返しましょう。\(d(F)=19\)なのでこの問題におけるA駅からF駅への最短距離は19であることが分かりました。
上図はA駅からF駅への最短経路を表しています。
今回紹介したダイクストラ法は辺の重みが非負の場合に使えるアルゴリズムです。そのため重みが負の辺を含むグラフだとダイクストラ法は使えません。そんなときは例えばベルマンフォード法が使えたりします。
\\\ ベルマンフォード法の解説記事はこちらから! ///
おわりに
いかがでしたか。
今回の記事ではダイクストラ法について解説していきました。
今後もこのような組合せ最適化に関する記事を書いていきます!
最後までこの記事を読んでくれてありがとうございました。





