こんにちは!しゅんです!
この記事では整数計画問題として定式化した最短経路問題と線形緩和してpythonで解いています。
最短経路問題はある地点からある地点までの最短距離を求める問題です。
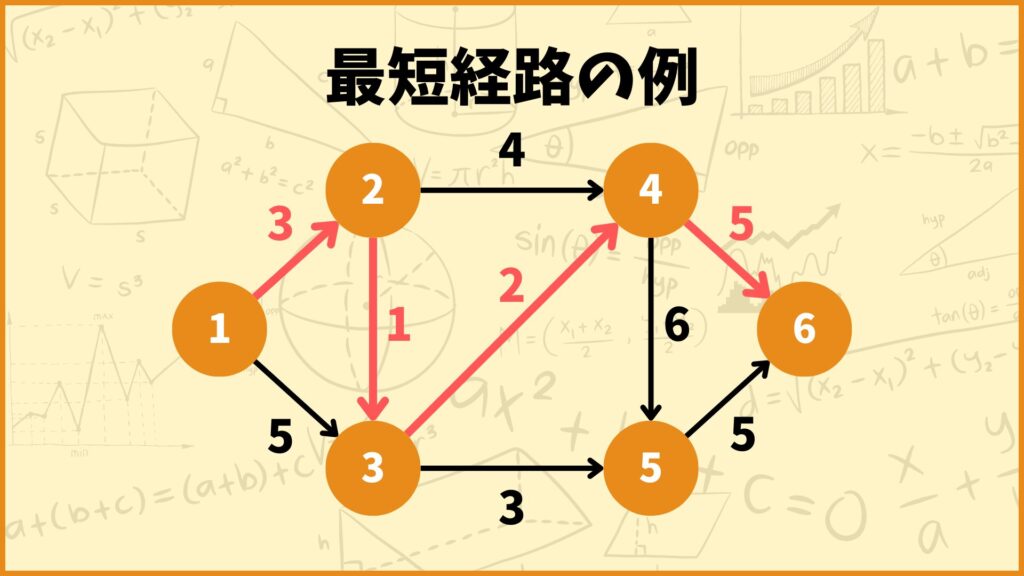
最短経路問題を整数計画問題として定式化する方法はこちらの記事で解説しています!
それではやっていきましょう!
普段は組合せ最適化の記事を書いてたりします。
ぜひ他の記事も読んでみてください!
このブログの簡単な紹介はこちらに書いてあります。
興味があったら見てみてください。
このブログでは経営工学を勉強している現役理系大学生が、経営工学に関することを色々話していきます!
ぼくが経営工学を勉強している中で感じたことや、興味深かったことを皆さんと共有出来たら良いなと思っています。
そもそも経営工学とは何なのでしょうか。Wikipediaによると
経営工学(けいえいこうがく、英: engineering management)は、人・材料・装置・情報・エネルギーを総合したシステムの設計・改善・確立に関する活動である。そのシステムから得られる結果を明示し、予測し、評価するために、工学的な分析・設計の原理・方法とともに、数学、物理および社会科学の専門知識と経験を利用する。
引用元 : 経営工学 – Wikipedia
長々と書いてありますが、要は経営、経済の課題を理系的な観点から解決する学問です。
問題設定と整数計画問題とpythonで解くためのコード
ここら辺は前回の記事で詳しく解説しているので今回は省略しています。
前回の記事はこちらから!
問題設定
今回解く問題は以下の通りです。
問題設定:
有向グラフ\(G = (V,E)\)と各辺\((i,j) \in E\)の重み\(w_{ij}(>0)\)がと始点\(s \in V\)、終点\(t \in V\)が与えられる。このとき始点\(s\)から終点\(t\)までの経路の中で経路中の辺の重みの合計が最小となるものを見つけたい。
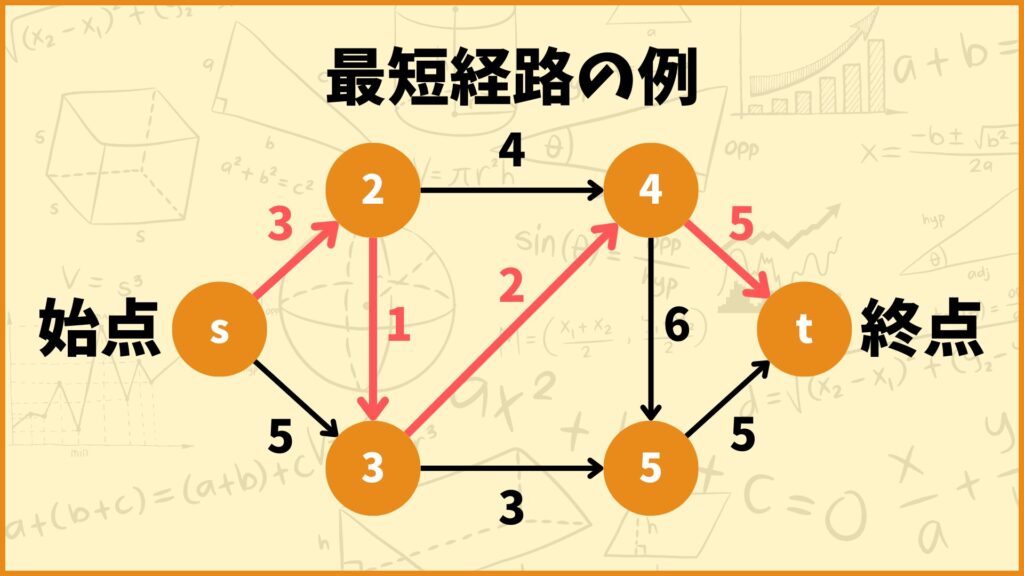
問題を簡単にするために始点に向かう辺、終点から出る辺は無いとします。
整数計画問題として定式化
この問題を整数計画問題として定式化すると以下のようになります。
パラメータ:
\(V\) : 頂点集合
\(E\) : 辺集合
\(w_{ij}\) : 辺\((i,j)\)の重み
変数:
\(x_{ij} \in \{0,1\}\) : 辺\((i,j)\)を採用するなら1、そうでないなら0を取る0-1変数
定式化:
\( \min \;\;\; \sum\limits_{(i,j) \in E}w_{ij}x_{ij}\)
\(\;\text{s.t.}\;\;\;\sum\limits_{j \in V,(s,j) \in E}x_{sj} = 1\)
\(\;\;\;\;\;\;\;\;\; \sum\limits_{j \in V,(j,t) \in E}x_{jt} = 1\)
\(\;\;\;\;\;\;\;\;\; \sum\limits_{i \in V,(i,j) \in E}x_{ij}-\sum\limits_{k \in V, (j,k) \in E}x_{jk} = 0 \;\;\; (\forall j \in V/\{s,t\})\)
\(\;\;\;\;\;\;\;\;\; x_{ij} \in \{0,1\} \;\;\; (\forall (i,j) \in E)\)
pythonで解くコード
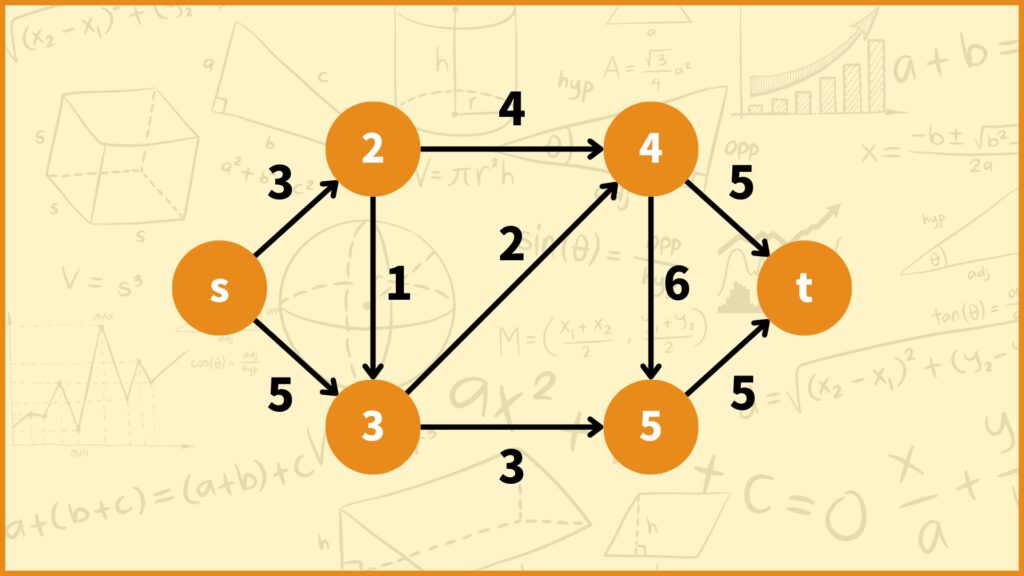
上のグラフの\(s \to t\)の最短経路をpythonで解くコードは以下の通りです。
## 事前準備
from pulp import *
## 記号の設定
V = [1,2,3,4,5,6] # 地点の設定
V_st = [2,3,4,5] # 始点と終点以外の地点の設定
E = [(1,2),(1,3),(2,3),(2,4),(3,4),(3,5),(4,5),(4,6),(5,6)] # 辺の設定
# 辺の重みの設定
w = {(1,2) : 3,
(1,3) : 5,
(2,3) : 1,
(2,4) : 4,
(3,4) : 2,
(3,5) : 3,
(4,5) : 6,
(4,6) : 5,
(5,6) : 5}
## 整数計画問題として定式化したものを解く
# 問題を最小化に設定
prob = pulp.LpProblem(sense = LpMinimize)
# 変数を設定
x = LpVariable.dicts("x", [(i,j) for (i,j) in E], cat="Binary")
# 目的関数を設定
prob += lpSum(w[(i,j)] * x[(i,j)] for (i,j) in E)
# 制約条件を設定
prob += lpSum(x[(1,j)] for j in V if (1,j) in E) == 1
prob += lpSum(x[(i,6)] for i in V if (i,6) in E) == 1
for j in V_st:
prob += lpSum(x[(i,j)] for i in V if (i,j) in E) - lpSum(x[(j,k)] for k in V if (j,k) in E) == 0
# 問題を解く
result = prob.solve()
## 結果の表示
# 解の状態を表示
print(LpStatus[result])
# 最適解の表示(値が1の変数だけ表示)
for (i,j) in E:
if x[i,j].value() == 1:
print(f"x_({i},{j}) =", x[i,j].value())
# 最適値の表示
print("最適値 :",prob.objective.value())
上のコードを実行すると以下のような結果が得られます。

線形緩和してpythonで解いてみる
それではさきほど整数計画問題として定式化したものを線形緩和してpythonで解いてみましょう。
パラメータ:
\(V\) : 頂点集合
\(E\) : 辺集合
\(w_{ij}\) : 辺\((i,j)\)の重み
変数:
\(x_{ij} \) : 連続変数に緩和
定式化:
\( \min \;\;\; \sum\limits_{(i,j) \in E}w_{ij}x_{ij}\)
\(\;\text{s.t.}\;\;\;\sum\limits_{j \in V,(s,j) \in E}x_{sj} = 1\)
\(\;\;\;\;\;\;\;\;\; \sum\limits_{j \in V,(j,t) \in E}x_{jt} = 1\)
\(\;\;\;\;\;\;\;\;\; \sum\limits_{i \in V,(i,j) \in E}x_{ij}-\sum\limits_{k \in V, (j,k) \in E}x_{jk} = 0 \;\;\; (\forall j \in V/\{s,t\})\)
\(\;\;\;\;\;\;\;\;\; x_{ij} \geq 0 \;\;\; (\forall (i,j) \in E)\)
変数を0-1変数から連続変数にして、制約条件に0以上というのを追加すればOKです。pythonで解くコードもそれらを変更すればOKです。
なお連続変数に緩和したので変数\(x_{ij}\)は任意の実数を取ることができます。そのため最適解の表示の所では値が0より大きい変数を全て出力するようにします。
問題例1

上のグラフの\(s \to t\)の最短経路を求めるコードは以下の通りです。
## 事前準備
from pulp import *
## 記号の設定
V = [1,2,3,4,5,6] # 地点の設定
V_st = [2,3,4,5] # 始点と終点以外の地点の設定
E = [(1,2),(1,3),(2,3),(2,4),(3,4),(3,5),(4,5),(4,6),(5,6)] # 辺の設定
# 辺の重みの設定
w = {(1,2) : 3,
(1,3) : 5,
(2,3) : 1,
(2,4) : 4,
(3,4) : 2,
(3,5) : 3,
(4,5) : 6,
(4,6) : 5,
(5,6) : 5}
## 整数計画問題として定式化したものを解く
# 問題を最小化に設定
prob = pulp.LpProblem(sense = LpMinimize)
# 変数を設定
x = LpVariable.dicts("x", [(i,j) for (i,j) in E], cat="Continuous")
# 目的関数を設定
prob += lpSum(w[(i,j)] * x[(i,j)] for (i,j) in E)
# 制約条件を設定
prob += lpSum(x[(1,j)] for j in V if (1,j) in E) == 1
prob += lpSum(x[(i,6)] for i in V if (i,6) in E) == 1
for j in V_st:
prob += lpSum(x[(i,j)] for i in V if (i,j) in E) - lpSum(x[(j,k)] for k in V if (j,k) in E) == 0
for (i,j) in E:
prob += x[(i,j)] >= 0
# 問題を解く
result = prob.solve()
## 結果の表示
# 解の状態を表示
print(LpStatus[result])
# 最適解の表示(値が0より大きい変数だけ表示)
for (i,j) in E:
if x[i,j].value() > 0:
print(f"x_({i},{j}) =", x[i,j].value())
# 最適値の表示
print("最適値 :",prob.objective.value())
このコードを実行したら以下のような結果が得られました。どうやら線形緩和しても整数解が得られていますね。これは偶然でしょうか。
問題例2
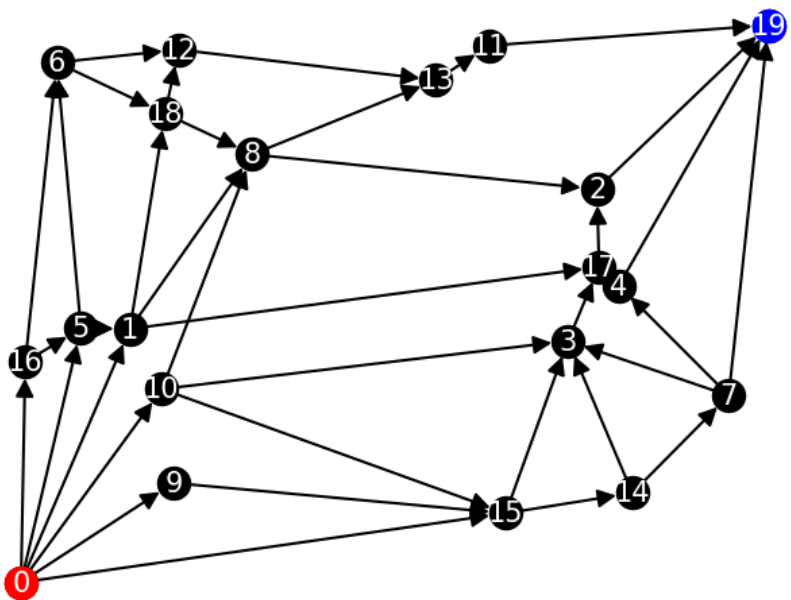
次に上のグラフの0から19までの最短経路を求めてみましょう。これも整数計画問題として定式化したものを線形緩和して求めます。なお頂点は\([0,10]\ times [0,10]\)のユークリッド平面所にランダムに配置し、2地点間の距離はユークリッド距離としています。
コードはさっきのモノと同じなので説明は省略します。
import random
random.seed(100)
V = [i for i in range(20)] # 始点0、終点19
V_st = V[1:-1] # 始点と終点を除く
s = V[0]
t = V[-1]
Pos = {}
w = {}
Pos[s] = [0,0]
Pos[t] = [10,10]
for i in V_st:
Pos[i] = (random.uniform(0,10),random.uniform(0,10))
E = [(0,16),(0,5),(0,1),(0,10),(0,9),(0,15),
(9,15),
(16,6),(16,5),
(5,1),(5,6),
(1,18),(1,8),(1,17),
(10,8),(10,15),(10,3),
(6,12),(6,18),
(18,12),(18,8),
(12,13),
(15,14),(15,3),
(14,7),(14,3),
(7,3),(7,4),(7,19),
(3,17),
(4,17),(4,19),
(17,2),
(2,19),
(8,13),(8,2),
(13,11),
(11,19)]
w = {}
for (i,j) in E:
w[(i,j)] = ((Pos[i][0] - Pos[j][0])**2 + (Pos[i][1] - Pos[j][1])**2)**(1/2)
## 整数計画問題として定式化したものを解く
# 問題を最小化に設定
prob = pulp.LpProblem(sense = LpMinimize)
# 変数を設定
x = LpVariable.dicts("x", [(i,j) for (i,j) in E], cat="Continuous")
# 目的関数を設定
prob += lpSum(w[(i,j)] * x[(i,j)] for (i,j) in E)
# 制約条件を設定
prob += lpSum(x[(s,j)] for j in V if (s,j) in E) == 1
prob += lpSum(x[(i,t)] for i in V if (i,t) in E) == 1
for j in V_st:
prob += lpSum(x[(i,j)] for i in V if (i,j) in E) - lpSum(x[(j,k)] for k in V if (j,k) in E) == 0
for (i,j) in E:
prob += x[(i,j)] >= 0
# 問題を解く
result = prob.solve()
## 結果の表示
# 解の状態を表示
print(LpStatus[result])
# 最適解の表示(値が1の変数だけ表示)
for (i,j) in E:
if i != t:
if j != s:
if x[(i,j)].value() > 0:
print(f"x_({i},{j}) =", x[(i,j)].value())
# 最適値の表示
print("最適値 :",prob.objective.value())
このコードを実行したら上のような結果が得られました。こちらも線形緩和しているのに整数解が得られていますね。これらは偶然なのでしょうか?
線形緩和しても整数の最適解が得られる
実は最短経路問題を整数計画問題として定式化したとき、線形緩和しても整数の最適解を得られることが知られています。
なぜなら制約条件の係数行列が完全単模行列(totally unimodular matrix)だからです。
完全単模行列ってなに?
完全単模行列:
任意の部分正方行列の行列式の値が0,1,-1のいずれかとなる行列
\(\begin{pmatrix} 1 & 1 \\ 1 & 0 \end{pmatrix}\;\;\; \begin{pmatrix} 1 & 1 & 0 \\ -1 & 0 & 1 \\ 0 & -1 & -1 \end{pmatrix} \;\;\; \begin{pmatrix} 1 & 1 & 1 & 0 & 0 \\ -1 & 0 & 0 & 1& 0 \\ 0 & -1 & 0 & 0 & 1 \\ 0 & 0 & -1 & -1 & -1 \end{pmatrix}\)
完全単模行列の例
上記の行列は完全単模行列の例です。
最短経路問題は係数行列が完全単模行列になる
実は最短経路問題を整数計画問題として定式化したときに、その制約条件の係数行列は有向グラフの接続行列になります。そして有向グラフの接続行列は完全単模行列であることが知られています。
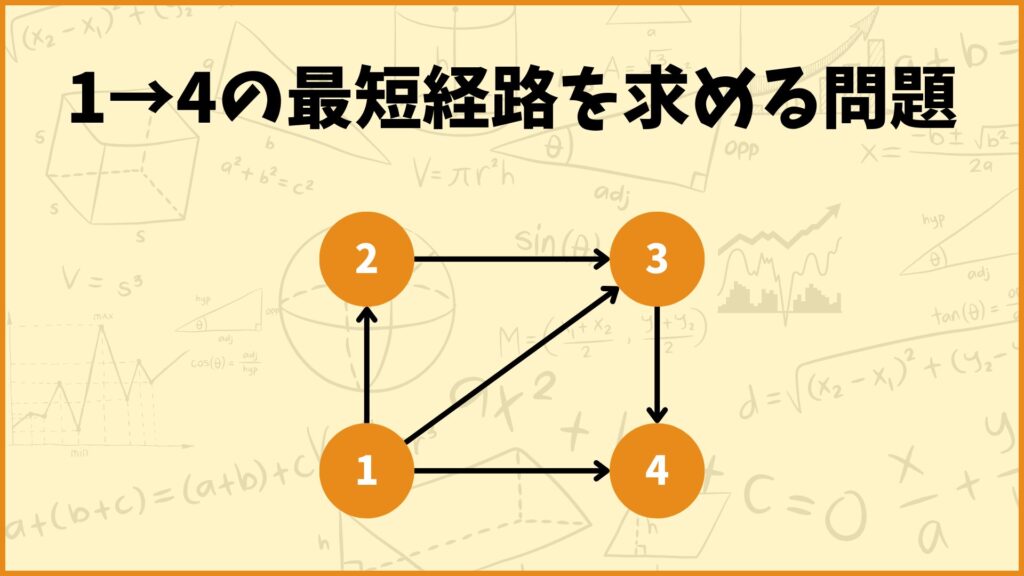
例えばこの問題を整数計画問題として定式化したときの制約条件は以下のようになります。なお分かりやすくするために\(\sum\)を使わずに書いています。
\(x_{12} + x_{13} + x_{14} = 1\)
\(x_{14} + x_{34} = 1\)
\(x_{12} – x_{23} = 0\)
\(x_{13} + x_{23} – x_{34} = 0\)
\(Ax=b\)の形で表すと以下のようになります。
\(\begin{pmatrix}1 & 1 & 1 & 0 & 0 \\ 0 & 0 & 1 & 0 & 1 \\ 1 & 0 & 0 & -1 & 0 \\ 0 & 1 & 0 & 1 & -1\end{pmatrix}\begin{pmatrix}x_{12} \\ x_{13} \\ x_{14} \\ x_{23} \\ x_{34}\end{pmatrix} = \begin{pmatrix}1 \\ 1 \\ 0 \\ 0\end{pmatrix}\)
ということで係数行列は
\(\begin{pmatrix}1 & 1 & 1 & 0 & 0 \\ 0 & 0 & 1 & 0 & 1 \\ 1 & 0 & 0 & -1 & 0 \\ 0 & 1 & 0 & 1 & -1\end{pmatrix}\)
となります。これが完全単模行列となるわけです。
おわりに
いかがでしたか。
今回の記事では最短経路問題について解説していきました。
今後もこのような数理最適化に関する記事を書いていきます!
最後までこの記事を読んでくれてありがとうございました。




