- シグモイド関数ってなに?
- pythonでシグモイド関数を実装したい…
- パーセプトロンにシグモイド関数を組み合わせるとどうなる?
こんにちは!しゅんです!
今回はシグモイド関数をpythonで実装する方法について解説していきます!
それではやっていきましょう!
普段は組合せ最適化の記事を書いてたりします。
ぜひ他の記事も読んでみてください!
このブログの簡単な紹介はこちらに書いてあります。
興味があったら見てみてください。
このブログでは経営工学を勉強している現役理系大学生が、経営工学に関することを色々話していきます!
ぼくが経営工学を勉強している中で感じたことや、興味深かったことを皆さんと共有出来たら良いなと思っています。
そもそも経営工学とは何なのでしょうか。Wikipediaによると
経営工学(けいえいこうがく、英: engineering management)は、人・材料・装置・情報・エネルギーを総合したシステムの設計・改善・確立に関する活動である。そのシステムから得られる結果を明示し、予測し、評価するために、工学的な分析・設計の原理・方法とともに、数学、物理および社会科学の専門知識と経験を利用する。
引用元 : 経営工学 – Wikipedia
長々と書いてありますが、要は経営、経済の課題を理系的な観点から解決する学問です。
シグモイド関数ってなに?
\(f(x) = \frac{1}{1+e^{-x}}\)
上の関数がシグモイド関数です。\(x\)に色んな値を代入してみると
\(f(0) = \frac{1}{1+e^0} = \frac{1}{1+1}=0.5\)
\(f(1) = \frac{1}{1+e^{-1}}=\frac{e}{e+1} ≒ 0.73\)
\(f(5) = \frac{1}{1+e^{-5}}=\frac{e^5}{e^5+1} ≒ 0.99\)
\(f(-1) = \frac{1}{1+e} ≒ 0.27\)
\(f(-5) = \frac{1}{1+e^5} ≒ 0.0067\)
という感じになります。またシグモイド関数をグラフで表すと下のようになります。
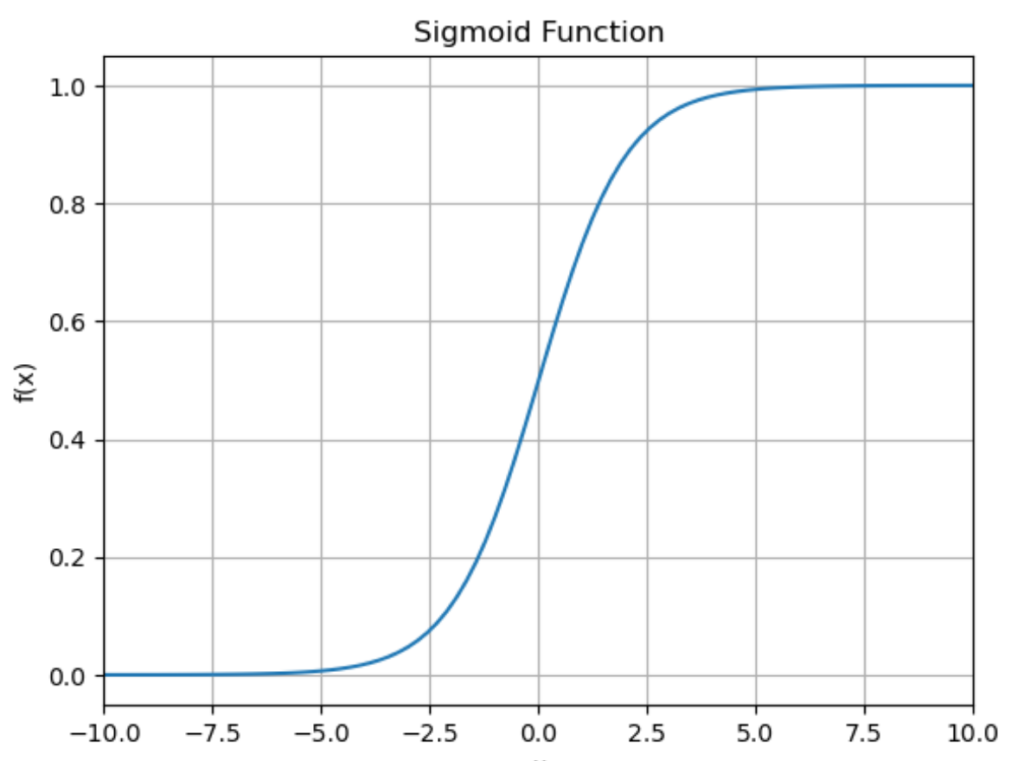
このグラフを見ると分かるように、シグモイド関数は\(x\)にどんな値を入力しても必ず0以上1以下の数字を返します。
シグモイド関数を微分してみよう!
\(f(x) = \frac{1}{1+e^{-x}}\)なので、\(f(x)\)を\(x\)で微分すると
\(f'(x) = -\frac{-e^{-x}}{(1+e^{-x})^2} = \frac{e^{-x}}{(1+e^{-x})^2}\)
となります。\(f'(x)\)をグラフで表すと以下のようになります。
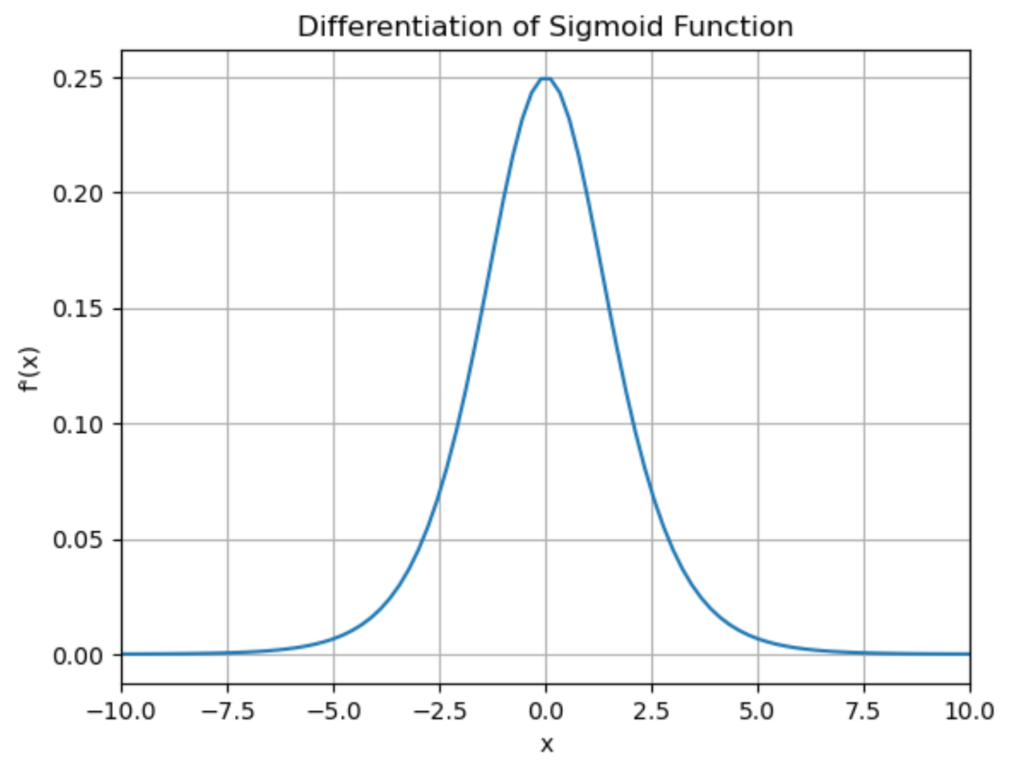
シグモイド関数をpythonで実装してみた
関数を実装してみた
それではシグモイド関数をpythonで実装してみましょう。
# numpyをインポート
import numpy as np
# シグモイド関数を定義
def sigmoid(x):
return 1 / (1 + np.exp(-x))
シグモイド関数はnumpyを使えばたった数行のコードで定義できます。numpyはpythonで数値計算を効率的にしてくれるライブラリで、指数関数、対数関数、三角関数などを1行で実装できます。
今回は\(e^{-x}\)を実装したいんですが、これは「np.exp(-x)」で実装できます。「x」に色々な数字を代入して結果を確認してみましょう。
for x in range(-10,11):
print(f"{x}を代入したときの値:{sigmoid(x)}")
-10から10まで「x」をfor文で回してシグモイド関数に代入したときの値を出力してみました。
グラフを描画してみた
それでは次にシグモイド関数のグラフを描画してみましょう。
# matplotlibをインポート
import matplotlib.pyplot as plt
# -10から10の範囲を100等分する
x = np.linspace(-10, 10, 100)
# xに対応するyを計算
y = sigmoid(x)
# グラフを描画
plt.plot(x, y)
plt.title("Sigmoid Function")
plt.xlabel("x")
plt.ylabel("f(x)")
plt.xlim(-10,10)
plt.grid(True)
plt.show()
上のコードではmatplotlibを使ってシグモイド関数のグラフを描画しています。
5行目では「np.linspace()」を使って-10から10の範囲を100等分したものを「x」としています。「x」を表示すると
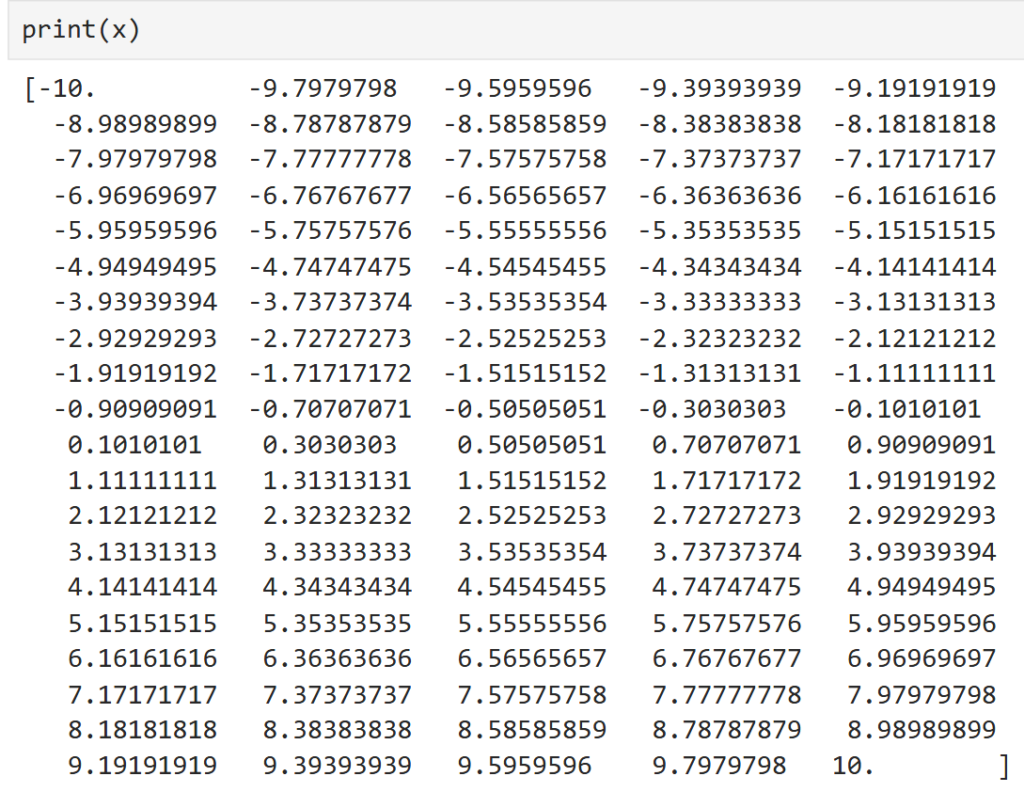
こんな感じでちゃんと-10~10の範囲を100等分しています。
8行目では今設定した「x」をシグモイド関数に代入したときの値を「y」としています。「y」の計算には先ほど定義した「sigmoid」関数を使っています。「y」を表示させると
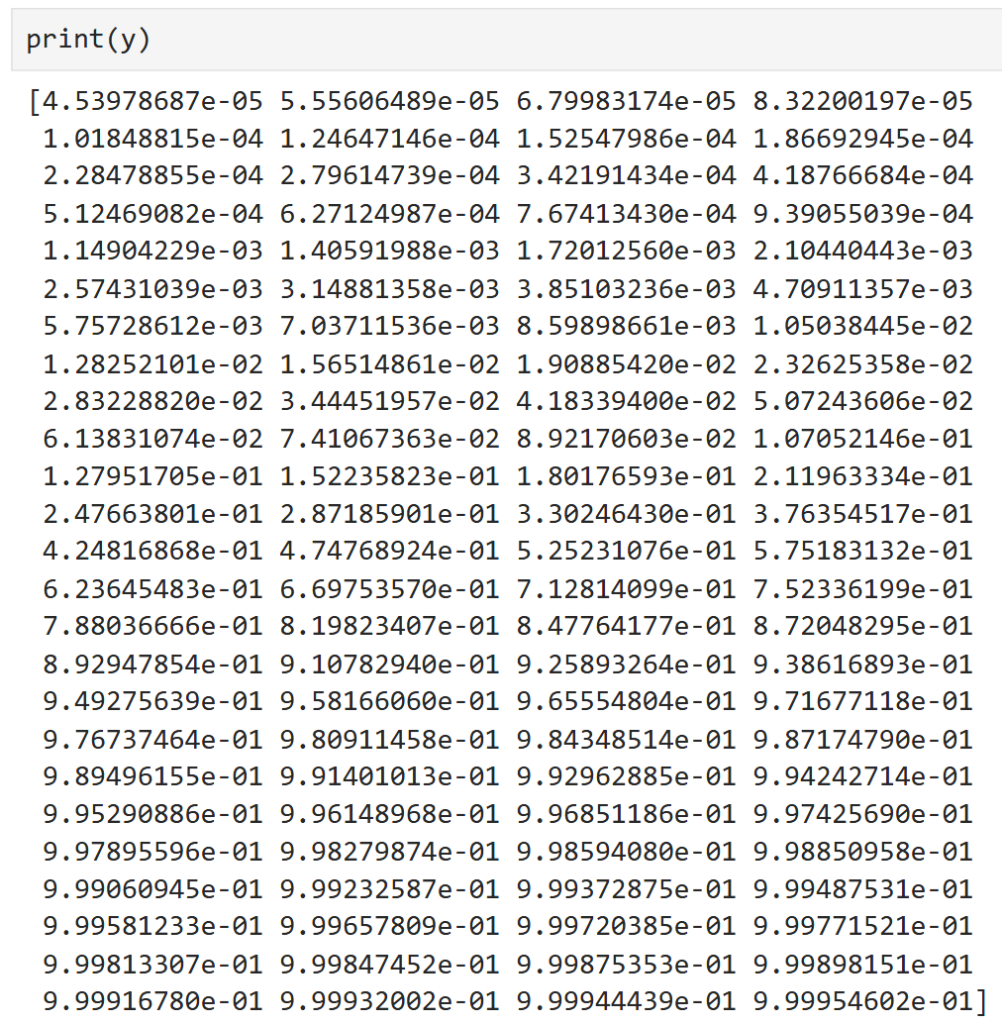
こんな感じで「x」中の各要素をシグモイド関数に代入したときの値になっています。
numpyの素晴らしい点は、「y」を計算するときfor文を使わずに1発で計算できることです。「x」には100個のデータが入っているので、普通に「y」を計算しようとしたらfor文で「x」中の要素1つ1つに対してシグモイド関数に代入する必要がありそうです。しかし「np.exp()」を使うことで「x」中の要素全てをいっぺんに計算することができ、計算時間を大幅に短縮することができます。
パーセプトロンにシグモイド関数を組み合わせるとどうなる?
それでは次にパーセプトロンにシグモイド関数を組み合わせてみましょう。
\\\ パーセプトロンの詳しい説明はこちらから! ///
パーセプトロンについて簡単に説明すると、\(n\)個の入力\(x\)に対して重み\(w\)とバイアス\(b\)を用いて以下の重み付き和
\(a=w_1x_1+w_2x_2+…+w_nx_n+b\)
を計算します。そしてこの重み付き和が0より大きかったら1、0以下だったら0を返すのがパーセプトロンです。このことを重み付き和を\(a\)として
\(f(a) = \begin{cases} 1 & (a > 0) \\ 0 & (a \leq 0) \end{cases}\)
と表すことにします。この式は、関数\(f\)は重み付き和\(a = w_1x_1+…+w_nx_n+b\)が0より大きかったら1、0以下だったら0を返すような関数であることを表しています。
この関数\(f\)をステップ関数と言ったりします。
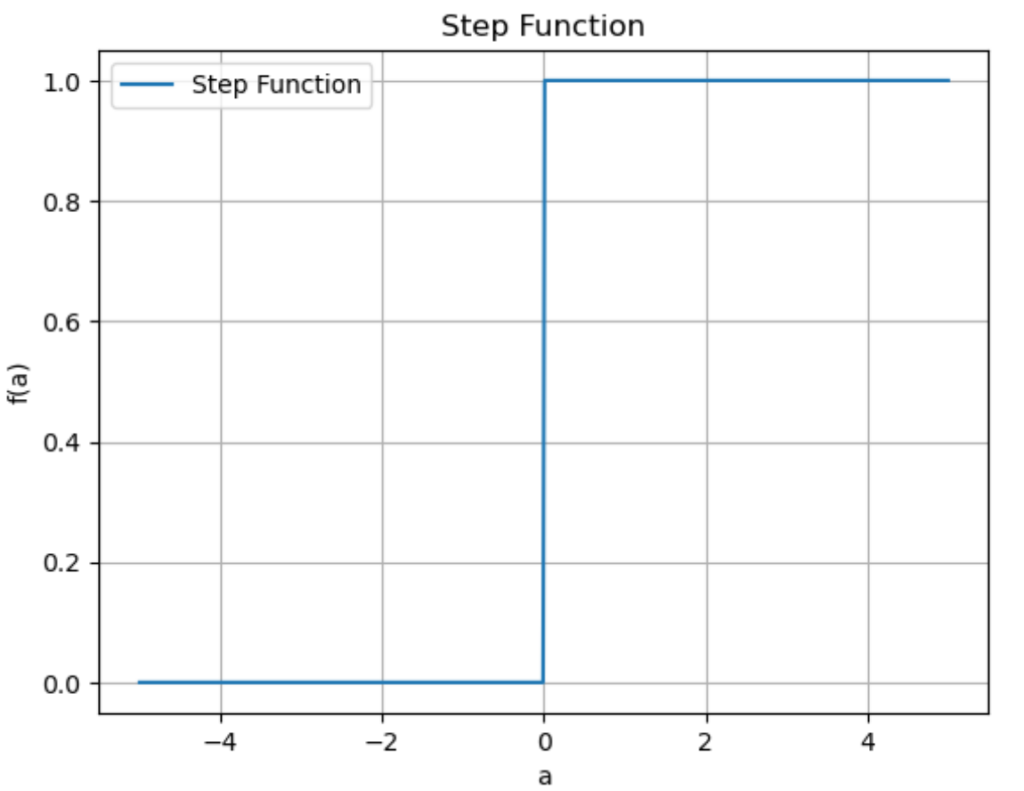
ステップ関数をグラフで表すと下のようになります。
import numpy as np
import matplotlib.pyplot as plt
def step_function(x):
return np.where(x > 0, 1, 0) # x>0なら1、そうでないなら0を返す
a = np.linspace(-5, 5, 500) # -5から5までを500等分した数値列
y = step_function(x)
plt.plot(a, y, label="Step Function")
plt.xlabel("a")
plt.ylabel("f(a)")
plt.title("Step Function")
plt.grid(True)
plt.legend()
plt.show()
丁度\(a = 0\)を境に0を返すか1を返すか分かれていますね。
このステップ関数をシグモイド関数に変更してみましょう。すなわち関数\(f\)をステップ関数からシグモイド関数に変更するわけです。
例えば\((x_1,x_2)=(1,2), (w_1,w_2)=(2,3),b=-9\)のとき重み付き和\(a\)は
\(a = w_1x_1+w_2x_2+b = 2\times1+3\times2-9 = -1\)
となりますが、もし関数\(f\)がステップ関数の場合
(ステップ関数の場合)\(f(a)=f(-1)=0\)
となります。一方関数\(f\)がシグモイド関数の場合
(シグモイド関数の場合)\(f(a)=f(-1)=\frac{1}{1+e} ≒ 0.27\)
と出力値が異なります。
この記事ではパーセプトロンにシグモイド関数を組み合わせることで出力値を変えましたが、他にも様々な関数が存在します。一般にこのような関数のことを活性化関数と言ったりします。
pythonでパーセプトロンとシグモイド関数を組み合わせてみた
コードの説明
それでは最後にpythonを使ってパーセプトロンとシグモイド関数を組み合わせましょう。
# numpyをインポート
import numpy as np
# シグモイド関数を定義
def sigmoid(x):
return 1 / (1 + np.exp(-x))
# パーセプトロンを定義
def perceptron(x,w,b):
a = np.dot(w,x) + b
return sigmoid(a)
#入力例
x = np.array([1, 2])
w = np.array([2, 3])
b = -9
print(perceptron(x,w,b))
2行目でnumpyをインポートしています。
5~6行目でシグモイド関数を定義しています。ここは先ほど説明したので省略します。
9~11行目でパーセプトロンを定義しています。基本的には前回記事で説明したものと同じですが、「return sigmoid(a)」の所だけ違い、シグモイド関数「sigmoid()」に重み付き和「a」を代入したものを返しています。
14~17行目で実際に数値を入力して結果を出力しています。このコードを実行すると

と出力されます。これは重みが\((w_1,w_2)=(2,3)\)、バイアスが\(b=-9\)のとき、\((x_1,x_2)=(1,2)\)をパーセプトロンに入力すると約0.27が返ってくるということを表しています。
色々な値を代入してグラフを作成する
それではこのパーセプトロンに色々な値を入力して結果をグラフにしてみましょう。
\((w_1,w_2)=(1,2), b=-5\)
## 事前準備
import matplotlib.pyplot as plt
import numpy as np
## シグモイド関数の定義
def sigmoid(x):
return 1 / (1 + np.exp(-x))
## パーセプトロンの定義
def perceptron(x, w, b):
a = np.dot(w, x) + b
return sigmoid(a)
## 重みとバイアスの設定
w = np.array([1, 2])
b = -3
## 入力値の生成
x1_range = np.arange(-5, 5.1, 0.1)
x2_range = np.arange(-5, 5.1, 0.1)
X1, X2 = np.meshgrid(x1_range, x2_range)
## 各入力値でのパーセプトロンの出力を計算
Z = np.zeros_like(X1)
for i in range(X1.shape[0]):
for j in range(X1.shape[1]):
x = np.array([X1[i, j], X2[i, j]])
Z[i, j] = perceptron(x, w, b)
## グラフの描画
plt.figure(figsize=(8, 6))
contour = plt.contourf(X1, X2, Z, cmap="coolwarm", alpha=0.8, levels=np.linspace(0, 1.0, 101))
plt.colorbar(contour, ticks=np.arange(0, 1.1, 0.1))
plt.xlabel("x1")
plt.ylabel("x2")
plt.title("Perceptron Outputs")
plt.show()
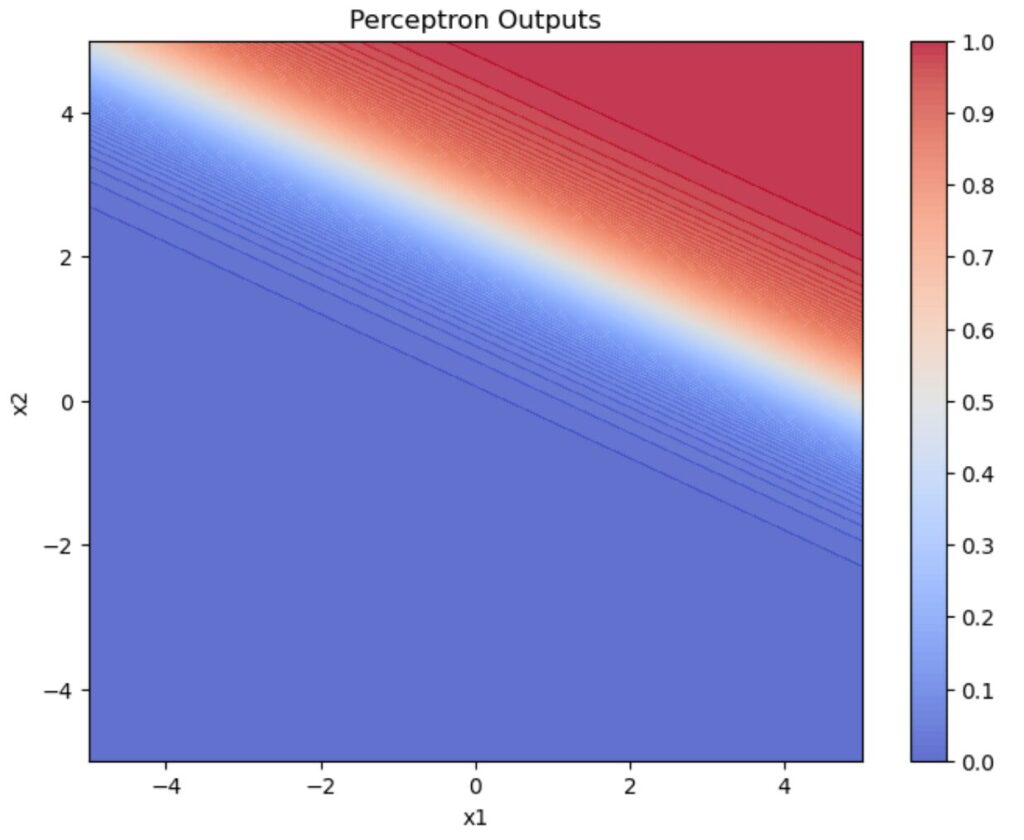
重みが\((w_1,w_2)=(1,2)\)、バイアスが\(b=-5\)のとき、入力値を\(-5 \leq x_1,x_2 \leq 5\)の範囲で動かしてパーセプトロンに入力したときの出力結果をグラフにしています。
グラフの色が出力値を表していて赤色が1、青色が0、白色が0.5とグラデーションになっています。シグモイド関数の定義から、出力値が0.5になるのは重み付き和が0になるときです。すなわち今回の例で言うと
\(w_1x_1+w_2x_2+b=0 \to x_1+2x_2 = 5\)
という直線が出力値が0.5になるラインです。つまり上図の白色の直線が\(x_1+2x_2 = 5\)となっています。
活性化関数がステップ関数の場合と比べてみましょう。
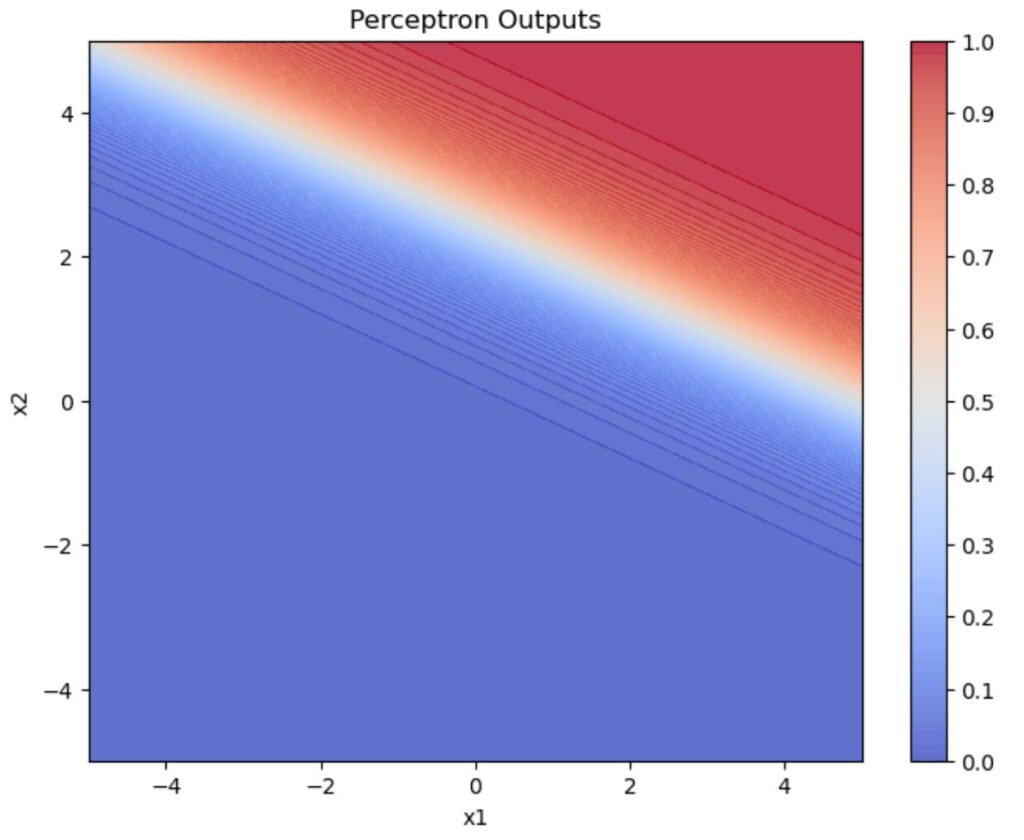
シグモイド関数
ステップ関数
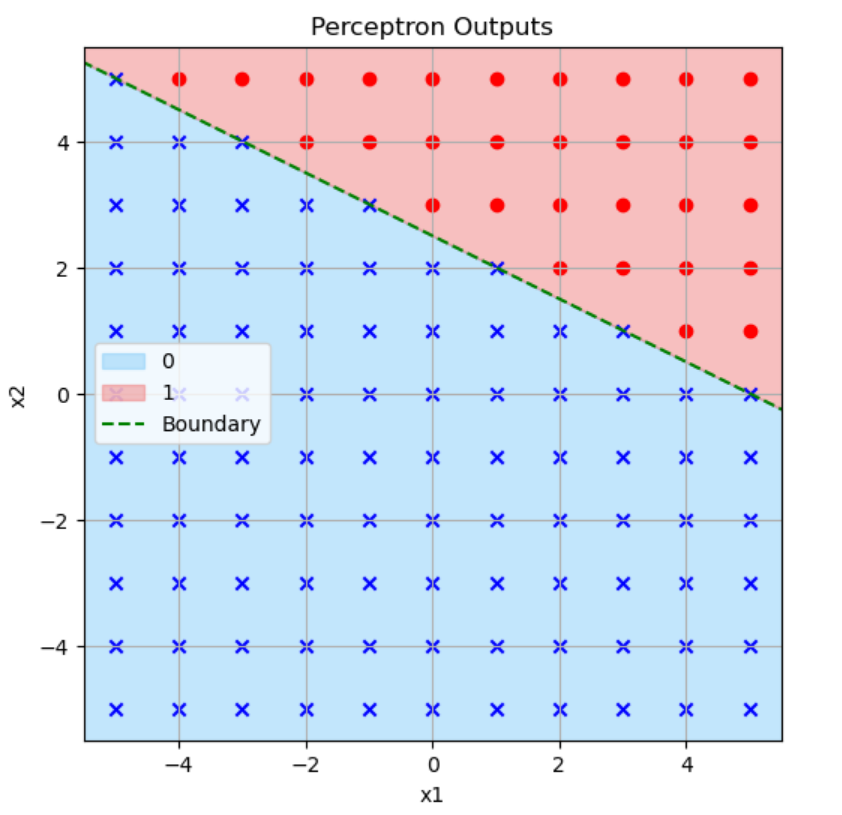
この2つのグラフは似ていますね。シグモイド関数のグラフの白いライン(出力値が0.5)の所がステップ関数のグラフの緑色の点線(境界)と対応しています。
イメージとしてはステップ関数は緑色の点線を境に0か1かはっきり分けるのに対し、シグモイド関数は0~1までグラデーションを作るという感じです。
\((w_1,w_2)=(3,-5), b=10\)
## 事前準備
import matplotlib.pyplot as plt
import numpy as np
## シグモイド関数の定義
def sigmoid(x):
return 1 / (1 + np.exp(-x))
## パーセプトロンの定義
def perceptron(x, w, b):
a = np.dot(w, x) + b
return sigmoid(a)
## 重みとバイアスの設定
w = np.array([3, -5])
b = 10
## 入力値の生成
x1_range = np.arange(-5, 5.1, 0.1)
x2_range = np.arange(-5, 5.1, 0.1)
X1, X2 = np.meshgrid(x1_range, x2_range)
## 各入力値でのパーセプトロンの出力を計算
Z = np.zeros_like(X1)
for i in range(X1.shape[0]):
for j in range(X1.shape[1]):
x = np.array([X1[i, j], X2[i, j]])
Z[i, j] = perceptron(x, w, b)
## グラフの描画
plt.figure(figsize=(8, 6))
contour = plt.contourf(X1, X2, Z, cmap="coolwarm", alpha=0.8, levels=np.linspace(0, 1.0, 101))
plt.colorbar(contour, ticks=np.arange(0, 1.1, 0.1))
plt.xlabel("x1")
plt.ylabel("x2")
plt.title("Perceptron Outputs")
plt.show()
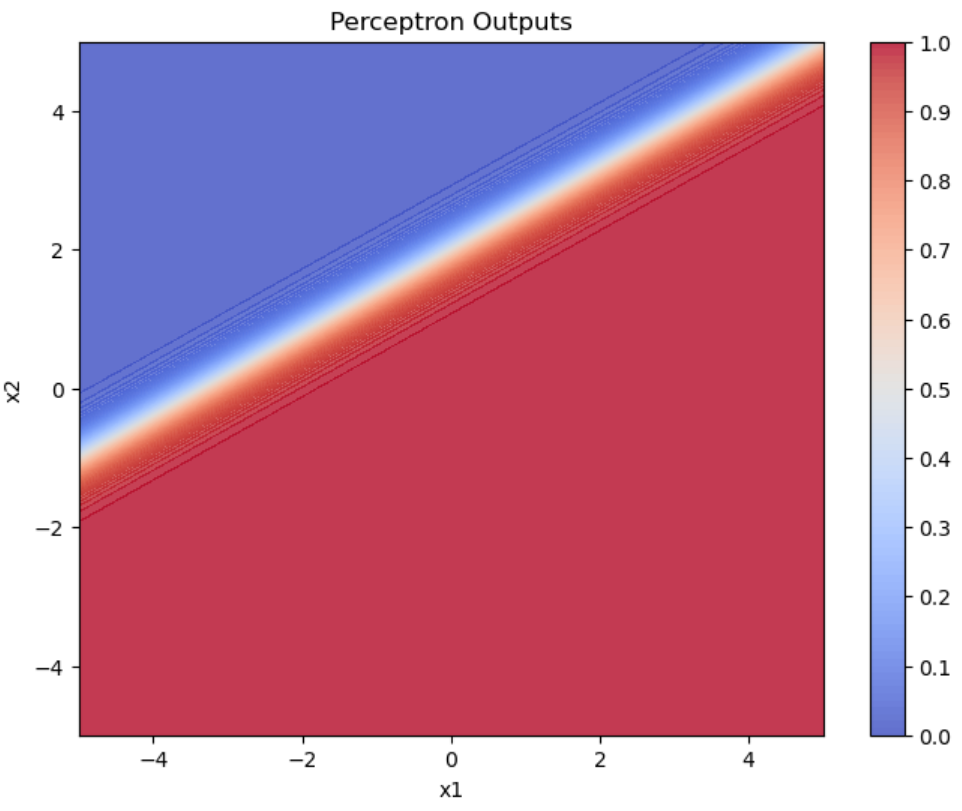
重みが\((w_1,w_2)=(3,-5)\)、バイアスが\(b=10\)のとき、入力値を\(-5 \leq x_1,x_2 \leq 5\)の範囲で動かしてパーセプトロンに入力したときの出力結果をグラフにしています。
グラフの色が出力値を表していて赤色が1、青色が0、白色が0.5とグラデーションになっています。シグモイド関数の定義から、出力値が0.5になるのは重み付き和が0になるときです。すなわち今回の例で言うと
\(w_1x_1+w_2x_2+b=0 \to 3x_1-5x_2 = -10\)
という直線が出力値が0.5になるラインです。つまり上図の白色の直線が\(3x_1-5x_2 = -10\)となっています。
活性化関数がステップ関数の場合と比べてみましょう。
シグモイド関数

ステップ関数
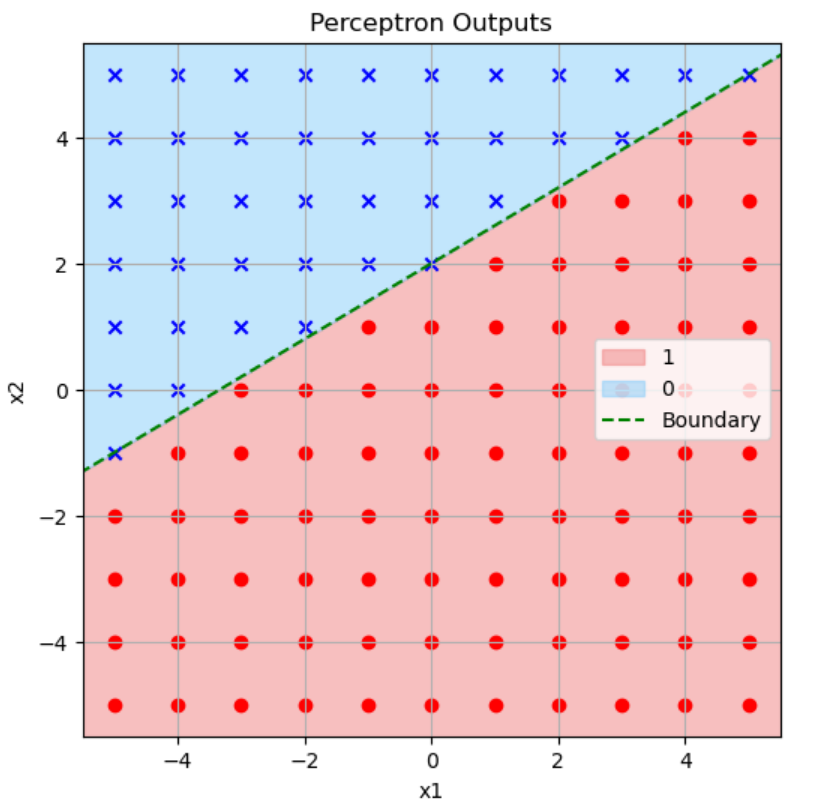
この2つのグラフは似ていますね。シグモイド関数のグラフの白いライン(出力値が0.5)の所がステップ関数のグラフの緑色の点線(境界)と対応しています。
イメージとしてはステップ関数は緑色の点線を境に0か1かはっきり分けるのに対し、シグモイド関数は0~1までグラデーションを作るという感じです。
おわりに
いかがでしたか。
今回の記事ではシグモイド関数を解説しました。
今後もこのようなAI・機械学習に関する記事を書いていきます!
最後までこの記事を読んでくれてありがとうございました。
参考文献



