こんにちは!しゅんです!
今回の記事では歪度について説明していきたいと思います!
歪度は統計やデータ分析を勉強するときに登場する数学用語です。この記事では歪度がいったい何を表しているのか、どうやって計算するのかを1つずつ丁寧に説明していきます!
今回のテーマは
・手計算で歪度を求める
・pythonで歪度を求める ← 今回はこっち!
の2部構成になっています!
手計算で歪度を求める方を解説している記事はこちらから!
それではやっていきましょう!
普段は統計検定2級の記事を書いてたりします。
ぜひ他の記事も読んでみてください!
このブログの簡単な紹介はこちらに書いてあります。
興味があったら見てみてください。
このブログでは経営工学を勉強している現役理系大学生が、経営工学に関することを色々話していきます!
ぼくが経営工学を勉強している中で感じたことや、興味深かったことを皆さんと共有出来たら良いなと思っています。
そもそも経営工学とは何なのでしょうか。Wikipediaによると
経営工学(けいえいこうがく、英: engineering management)は、人・材料・装置・情報・エネルギーを総合したシステムの設計・改善・確立に関する活動である。そのシステムから得られる結果を明示し、予測し、評価するために、工学的な分析・設計の原理・方法とともに、数学、物理および社会科学の専門知識と経験を利用する。
引用元 : 経営工学 – Wikipedia
長々と書いてありますが、要は経営、経済の課題を理系的な観点から解決する学問です。
歪度ってなに?
まず初めに歪度をザックリ説明すると
データの分布がどれだけ偏っているかを表す指標
です。と言っても言葉だけでは説明してもよくわからないので具体的なグラフを使って説明したいと思います。
グラフを使って歪度を理解する

上にある3つのヒストグラムについて考えてみましょう。この3つのヒストグラムはデータの偏り具合が全然違いますね。
ヒストグラムA:データの分布が左に偏っている
ヒストグラムB:データの分布が偏っていない(左右対称)
ヒストグラムC:データの分布が右に偏っている
まずヒストグラムAを見てみましょう。これを見るとデータが結構左側に偏っていますね。例えばこのヒストグラムがテストの点数分布だとしましょう。横軸が点数、縦軸が人数のヒストグラムだと考えると、このテストは結構みんな点数が取れなかったのかなと推測できます。テストが結構難しかったのかなと分析できますね。
次にヒストグラムBを見てみましょう。これを見るとデータは特に偏っておらず、ほぼ左右対称な分布になっています。これもテストの点数分布だと思って考えてみましょう。ヒストグラムBの場合はいい感じにテストの点数が散らばっています。おそらくこのテストは難しすぎず簡単すぎずちょうど良い感じのテストだったんだと推測できます。
最後にヒストグラムCを見てみましょう。これを見るとデータが結構右側に偏っていますね。これもヒストグラムがテストの点数分布だとして考えましょう。このテストは結構みんな点数が取れたのかなと推測できます。テストが結構簡単だったのかなと分析できますね。
このように分布の偏り具合はデータがどういうものかを知る上で非常に重要なんです。
そしてこの偏り具合をちゃんと数値化したものが歪度になります。
3つのヒストグラムとそれらの歪度
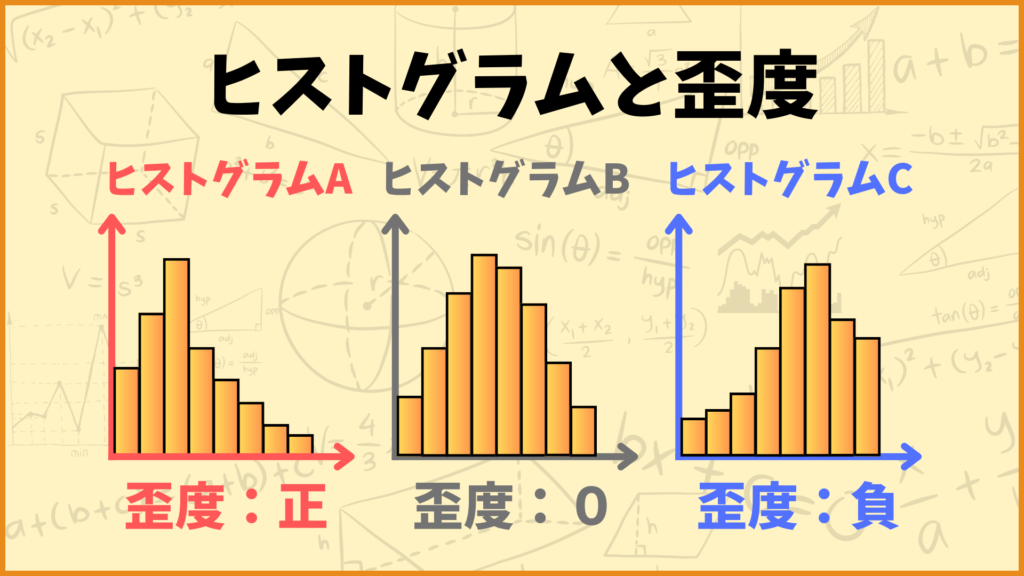
それでは3つのヒストグラムとそれらの歪度について見ていきましょう。
分布が左に偏っている(ヒストグラムA):歪度は正の値を取る
分布が偏っていない(ヒストグラムB):歪度は0に近い値を取る
分布が右に偏っている(ヒストグラムC):歪度は負の値を取る
データの分布が左側に偏っていると歪度の値は正の値を取ります。左に偏れば偏るほどその値はどんどん大きくなります。
一方データの分布が右側に偏っていると歪度の値は負の値になります。右に偏れば偏るほどその値はどんどん小さくなります。
データの分布に偏りが無くなれば無くなるほど0に近くなります。分布が完全に左右対称になると歪度は0を取ります。
pythonを使えばデータ数が多い場合も歪度を計算できる
データ数が少ない場合は自分で計算して歪度を求めることが可能ですが、データ数が多くなると手計算で歪度を求めるのは現実的に難しくなります。
ということでこの記事ではデータ数が多くて手計算できない場合に、pythonを使って歪度を求める方法を紹介したいと思います!
歪度を手計算で求める方法はこちらの記事で説明しています!
今回は歪度を計算する関数を作る方法と、scipyを使って一発で歪度を求める方法の2種類を紹介したいと思います。
pythonで歪度を求める方法 その1
それではまず歪度を計算する関数を作成してみましょう。結論以下のようにコードを書くことで歪度を求めることができます。
## 事前準備
import numpy as np
## 歪度を求める関数を定義
def skewness(data):
n = len(data) #データ数を取得
Mean = data.mean() #データの平均値を求める
Std = data.std(ddof = 0) #(標本)標準偏差を求める
SDC = ((data-Mean)**3).sum() #偏差の3乗の和(the sum of the cubes of the deviations)を求める
MDC = SDC/n #偏差の3乗の平均(the mean of the cube of the deviation)を求める
Skew = MDC/(Std**3) #歪度(Skewness)を求める
return Skewそれでは1つずつ解説していきます!
事前準備
今回はnumpyを使って計算をしたいと思います。numpyはpythonで数値計算を効率的に行うために使うやつです。数字を扱う場面ではかなりの頻度で使います。
numpyはインポートしないと使えないので1~2行目でインポートしています。後ろにas npと書いてありますが、これはnumpyをこれ以降npって省略して書くよって言っています。
## 事前準備
import numpy as np関数の定義
事前準備が終わったのでいよいよ歪度を求める関数を定義したいと思います。とは言っても歪度を求めるための計算を1つずつ設定しているだけです。歪度の計算式は前回の記事で解説しています。
少し専門的な話
今回は分かりやすいので標本歪度の説明をしたいと思います。つまりこの3つのデータをそれぞれ標本だと考えて、歪度を\(\frac{\frac{1}{n}\sum\limits^n_{i=1}(x_i – \bar{x})^3}{s^3}\)として計算したいと思います。
(\(s\)は標本標準偏差)
歪度の計算式はこちらの記事で説明しています!
今回はnumpyのndarray形式のデータが入力されたときにそのデータの歪度を返すような関数を作ります。6行目でその関数を定義することを宣言しています。名前はskewnessにしました。
def skewness(data):
8行目でデータの個数を取得してnという名前を付けてます。len(data)でdataの長さを求めることができます。例えばdata=np.array([1,1,2,2,3])だったらlen(data)=5となります。
n = len(data) #データ数を取得
9行目でデータの平均値、10行目でデータの(標本)標準偏差を求めています。どちらもこの後の計算で必要になるのでそれぞれMean, Stdと名前を付けています。
Mean = data.mean() #データの平均値を求める
Std = data.std(ddof = 0) #(標本)標準偏差を求める
11行目では偏差の3乗和\(\sum\limits^n_{i=1}(x_i-\bar{x})^3\)を求めています。dataはndarray形式なのでMeanを引くことでdata中の全ての要素\(x_i\)から\(\bar{x}\)を引き算した値、すなわち偏差\(x_i-\bar{x}\)が求められます。後は全ての\(i\)に対して\(x_i-\bar{x}\)を3乗して足せば偏差の3乗和を求めることができます。
SDC = ((data-Mean)**3).sum() #偏差の3乗の和(the sum of the cubes of the deviations)を求める
12行目では偏差の3乗の平均を求めています。先ほど求めた偏差の3乗和をデータの個数\(n\)で割ることで、偏差の3乗の平均\(\frac{1}{n}\sum\limits^n_{i=1}(x_i-\bar{x})^3\)を求めることができます。
MDC = SDC/n #偏差の3乗の平均(the mean of the cube of the deviation)を求める
13行目ではこれまで計算した値を使って歪度を求めています。歪度は偏差の3乗の平均を標準偏差の3乗で割れば計算できます。
Skew = MDC/(Std**3) #歪度(Skewness)を求める
15行目で今求めた歪度Skewを返しています。
return Skew
ということで歪度を求める関数skewnessの定義ができました。
データを入力して歪度を計算してみる
それでは今作った関数を使って歪度を計算してみましょう。今回は\(\lambda=2\)のポアソン分布に従う1000個の乱数をデータ値としたいと思います。
ポアソン分布はこちらの記事で説明しています!
numpyのrandom.poisson()でポアソン分布に従う乱数を生成することができます。lamでパラメータ\(\lambda\)の値、sizeで乱数の個数をそれぞれ設定できます。今回は\(\lambda=2\)のポアソン分布に従う乱数を1000個生成して、さっき定義したskewness関数でそのランダムデータの歪度を求めています。
## ポアソン分布に従うランダムなデータを生成して歪度を求める
np.random.seed(1)
data = np.random.poisson(lam=2, size = 1000)
## 歪度を表示
skewness(data)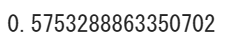
np.random.seed()で乱数の値を固定することができます。これをしないと毎回データ値が変わるので、出力される歪度が毎回変わってしまって不便なんです。括弧の中の数値によって固定されるランダム値が決まります。適当に設定して大丈夫です。
ということで歪度が計算できました。結果を見ると約0.58なので、割と左に偏っているデータだということが分かりますね。
ヒストグラムでデータの偏りを確認する
最後にこのデータをヒストグラムにしてデータがどんな分布なのかを確認してみましょう。ヒストグラムの描画にはmatplotlibを使います。matplotlibはpythonでグラフを扱いたいときによく使うやつです。
今回は歪度の計算がメインなのでヒストグラムを描くコードの説明は省略します。
# matplotlibをインポートする
import matplotlib.pyplot as plt
# ヒストグラムを描く
hist, bins = np.histogram(data, bins=np.arange(0, 10), density=True)
plt.bar(bins[:-1], hist, width=0.9, alpha=0.6, color="blue")
plt.xlabel("Number")
plt.ylabel("Frequency")
plt.xticks(np.arange(0,9,1))
plt.title("Histogram")
plt.show()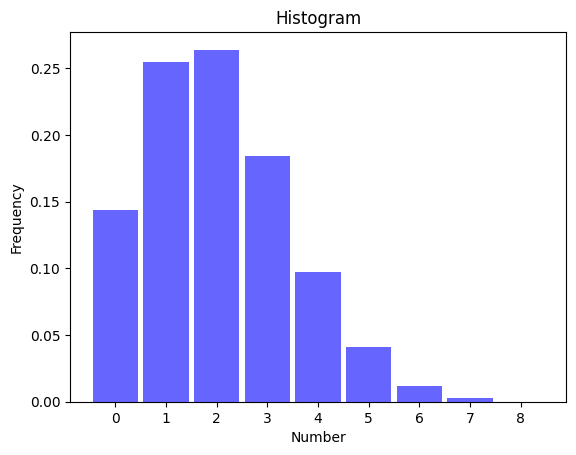
横軸が数字、縦軸がデータの生成割合です。例えばdataの中に1がある割合は約0.25です。これを見るとデータの分布が左に偏っていることが分かります。歪度が正であることと一致していますね。
ヒストグラムはこちらの記事で説明しています!
pythonで歪度を求める方法 その2
次にscipyを使って歪度を一発で求める方法を紹介したいと思います。まずはscipyから歪度を求める関数skewをインポートします。scipyはpythonで統計を使うときによく使います。
# scipyからskewをインポートする
from scipy.stats import skew
skewは歪度を求める関数です。これを使えば一発でデータの歪度を求められます。
# 歪度を求める
skew(data)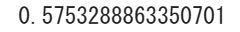
ということで歪度を求める方法その1のときと同じ値が出力されました。歪度を計算する場合はこっちの方が格段に楽ですね。
おわりに
いかがでしたか。
今回の記事ではpythonで歪度を求める方法について解説していきました。
今後もこのような統計に関する記事を書いていきます!
最後までこの記事を読んでくれてありがとうございました。