【これでわかる！】数独を整数計画問題として定式化してpythonで解く方法をなるべくわかりやすく解説してみた

この記事で解決できること

数独を整数計画問題として定式化したい…
数独をpythonで解くコードを実装したい…

はじめに

こんにちは！しゅんです！

この記事では数独を整数計画問題として定式化してpythonで解く方法を解説しています！

数独は下の図のようなやつです。

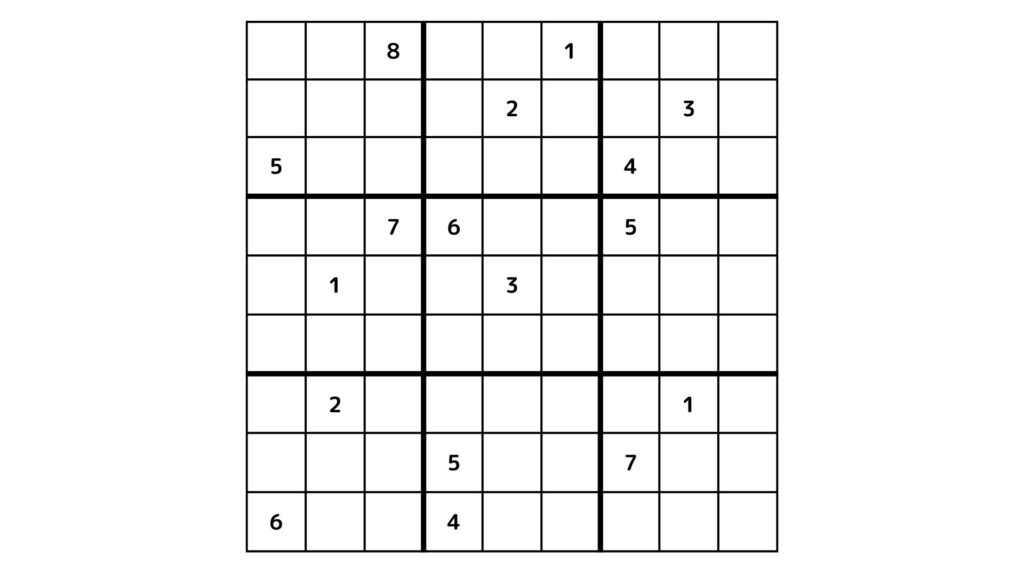
今回は数独を解くプログラムを作って実際に上の問題を解いてみようと思います。

この数独はこちらのサイトから引用しました。
数独-超難問10選！【解き方やコツ】最難問のナンプレにチャレンジ！｜りゅ～く.net (ryu-ku.net)

それではやっていきましょう！

普段は組合せ最適化の記事を書いてたりします。
ぜひ他の記事も読んでみてください！

もっとみる

このブログの簡単な紹介はこちらに書いてあります。
興味があったら見てみてください。

このブログについて

このブログでは経営工学を勉強している現役理系大学生が、経営工学に関することを色々話していきます！

ぼくが経営工学を勉強している中で感じたことや、興味深かったことを皆さんと共有出来たら良いなと思っています。

そもそも経営工学とは何なのでしょうか。Wikipediaによると

経営工学（けいえいこうがく、英: engineering management）は、人・材料・装置・情報・エネルギーを総合したシステムの設計・改善・確立に関する活動である。そのシステムから得られる結果を明示し、予測し、評価するために、工学的な分析・設計の原理・方法とともに、数学、物理および社会科学の専門知識と経験を利用する。

引用元 : 経営工学 – Wikipedia

長々と書いてありますが、要は経営、経済の課題を理系的な観点から解決する学問です。

数独を解くプログラム

今回作ったプログラムは以下の通りです。

## 必要なライブラリのインポート
import pulp


## sudokuという関数を定義する
def sudoku(INITIAL) :
  
  # 定式化で使う文字の定義
  NUM = [1,2,3,4,5,6,7,8,9]
  BOX = [[1,2,3],[4,5,6],[7,8,9]]

  # 問題の生成
  problem = pulp.LpProblem("sudoku",pulp.LpMinimize)

  # 変数の定義
  var = pulp.LpVariable.dicts("sudoku",(NUM,NUM,NUM) , cat='Binary')

  # 目的関数の設定(ダミー)
  problem += pulp.lpSum(var)

  # 制約条件の設定
  # 1つのマスには1つしか文字が入らない
  for x in NUM:
    for y in NUM:
      problem += pulp.lpSum(var[x][y][n] for n in NUM) == 1

  # 最初から数字が分かっているマスには他の数字は入らない
  for [x,y,n] in INITIAL:
    problem += var[x][y][n] == 1
  
  # 1つの行に同じ数字は1つ
  for x in NUM:
    for n in NUM:
      problem += pulp.lpSum(var[x][y][n] for y in NUM) == 1
  
  # 1つの列に同じ数字は1つ
  for y in NUM:
    for n in NUM:
      problem += pulp.lpSum(var[x][y][n] for x in NUM) == 1

  # １つのボックスに同じ数字は1つ
  for rows in BOX:
    for columns in BOX:
      for n in NUM:
        problem += pulp.lpSum(var[x][y][n] for x in rows for y in columns) == 1

  # 問題を解く
  result = problem.solve()
  # 結果を格納する空の9×9の二次元リストを作成
  result_list =[[] for i in range(9)]
  # 変数の値が1のものをresult_listに追加
  for x in NUM:
    for y in NUM:
      for n in NUM:
        if pulp.value(var[x][y][n]) == 1:
          result_list[x-1].append(n)

  return result_list


## 問題を解く
# 初期値を設定する
INITIAL = [[1,3,8],[1,6,1],
           [2,5,2],[2,8,3],
           [3,1,5],[3,7,4],
           [4,3,7],[4,4,6],[4,7,5],
           [5,2,1],[5,5,3],
           [7,2,2],[7,8,1],
           [8,4,5],[8,7,7],
           [9,1,6],[9,4,4]]
# 解を取得する
ans = sudoku(INITIAL)
# 解を表示する
for row in ans:
    print(row)

今回は整数計画問題として定式化して解きました。このコードを実行したら上図の結果が得られました。それでは1つずつコードの解説していきます。

必要なライブラリのインポート

## 必要なライブラリのインポート
import pulp

まず最初にpulpをインポートします。pulpはpythonで数理最適化の問題を扱うときに使えるライブラリです。

数独を解く関数を定義する

## sudokuという関数を定義する
def sudoku(INITIAL) :
  
  # 定式化で使う文字の定義
  NUM = [1,2,3,4,5,6,7,8,9]
  BOX = [[1,2,3],[4,5,6],[7,8,9]]

  # 問題の生成
  problem = pulp.LpProblem("sudoku",pulp.LpMinimize)

  # 変数の定義
  var = pulp.LpVariable.dicts("sudoku",(NUM,NUM,NUM) , cat="Binary")

  # 目的関数の設定(ダミー)
  problem += pulp.lpSum(var)

  # 制約条件の設定
  # 1つのマスには1つしか文字が入らない
  for x in NUM:
    for y in NUM:
      problem += pulp.lpSum(var[x][y][n] for n in NUM) == 1

  # 初めから数字が分かっているマスの変数は1にする
  for [x,y,n] in INITIAL:
    problem += var[x][y][n] == 1
  
  # 1つの行に同じ数字は1つ
  for x in NUM:
    for n in NUM:
      problem += pulp.lpSum(var[x][y][n] for y in NUM) == 1
  
  # 1つの列に同じ数字は1つ
  for y in NUM:
    for n in NUM:
      problem += pulp.lpSum(var[x][y][n] for x in NUM) == 1

  # １つのボックスに同じ数字は1つ
  for rows in BOX:
    for columns in BOX:
      for n in NUM:
        problem += pulp.lpSum(var[x][y][n] for x in rows for y in columns) == 1

  # 問題を解く
  result = problem.solve()
  # 結果を格納する空の9×9の二次元リストを作成
  result_list =[[] for i in range(9)]
  # 変数の値が1のものをresult_listに追加
  for x in NUM:
    for y in NUM:
      for n in NUM:
        if pulp.value(var[x][y][n]) == 1:
          result_list[x-1].append(n)

  return result_list

次に数独を解く関数を定義します。ここは長いので1つずつ解説していきます。

関数として定義する

## 数独を解く関数を定義する
def sudoku(INITIAL) :

ここでは「sudoku」という名前の関数を定義しています。引数は「INITIAL」で、これは最初からどの数字が入るか分かっているマスの情報を持っている2次元リストです。

例えば1行2列目が3、3行7列目が9であることがすでに分かっている場合

INITIAL = [[1,2,3],[3,7,9]]

を「sudoku」関数に代入することになります。

定式化で使う文字の定義

  # 定式化で使う文字の定義
  NUM = [1,2,3,4,5,6,7,8,9]
  BOX = [[1,2,3],[4,5,6],[7,8,9]]

この後変数、目的関数、制約条件を設定するときに使う文字を先に定義しておきます。

問題の生成

  # 問題の生成
  problem = pulp.LpProblem("sudoku",pulp.LpMinimize)

ここでは数理計画問題を生成しています。引数の「”sudoku”」は問題の名前、「pulp.LpMinimize」は問題を最小化に設定しています。これ以降問題を指定するときは「problem」を使います。

変数の定義

  # 変数の定義
  var = pulp.LpVariable.dicts("sudoku",(NUM,NUM,NUM) , cat="Binary")

ここでは変数の定義をしています。変数は「pulp.LpVariable」で定義できます。一度にたくさん変数を定義したいときは「.dicts」を使うと楽です。

引数の「”sudoku”」は変数名、「(NUM,NUM,NUM)」は変数の添字の集合、「cat=”Binary”」は変数を0-1変数に設定することをそれぞれ表しています。

「var[x][y][n] = 1」は \(x\) 行 \(y\) 列目の数字が \(n\) であることを表します。

もっと深堀り！

変数が整数値しか取らない数理計画問題を整数計画問題と言います。一方で整数値しか取らない変数と整数じゃない値も取りうる変数の両方を持つ数理計画問題は混合整数計画問題と呼びます。

目的関数の設定

  # 目的関数の設定(ダミー)
  problem += pulp.lpSum(var)

ここでは目的関数を設定しています。といっても数独を解く上では目的関数がどんな形でも関係ないので適当に設定しています。

制約条件の設定

  # 制約条件の設定
  # 1つのマスには1つしか文字が入らない
  for x in NUM:
    for y in NUM:
      problem += pulp.lpSum(var[x][y][n] for n in NUM) == 1

  # 初めから数字が分かっているマスの変数は1にする
  for [x,y,n] in INITIAL:
    problem += var[x][y][n] == 1
  
  # 1つの行に同じ数字は1つ
  for x in NUM:
    for n in NUM:
      problem += pulp.lpSum(var[x][y][n] for y in NUM) == 1
  
  # 1つの列に同じ数字は1つ
  for y in NUM:
    for n in NUM:
      problem += pulp.lpSum(var[x][y][n] for x in NUM) == 1

  # １つのボックスに同じ数字は1つ
  for rows in BOX:
    for columns in BOX:
      for n in NUM:
        problem += pulp.lpSum(var[x][y][n] for x in rows for y in columns) == 1

ここでは制約条件を設定しています。たくさんあるので1つずつ説明していきます。

1つのマスに数字は1つしか入らない

  # 1つのマスには1つしか文字が入らない
  for x in NUM:
    for y in NUM:
      problem += pulp.lpSum(var[x][y][n] for n in NUM) == 1

これは

「1つのマスには1つしか文字が入らない」

という制約を表しています。

例えば3行4列のマスに入る数字が1だとします。これを数式で表すと

「var[3][4][1] = 1」

となります。このとき2～9の数字は3行4列には入りません。これを数式で表すと

「var[3][4][2] = var[3][4][3] = \(\cdots\) = var[3][4][9] = 0」

となります。これらをまとめると

「var[3][4][1] + var[3][4][2] + \(\cdots\) + var[3][4][9] = 1」

という式で表すことができます。この操作をすべての行と列で行います。

これをpulpで記述すると上のようになります。なおpulpで式を書くときは生成した問題（今回はproblem）に+=を付け、その後に式を書きます。

初めから数字が分かっているマスの変数は1にする

  # 初めから数字が分かっているマスの変数は1にする
  for [x,y,n] in INITIAL:
    problem += var[x][y][n] == 1

この制約は

「初めから数字が分かっているマスの変数は1にする」

と言うことを表しています。初めから数字が分かっているマスの情報は「INITIAL」として与えられているので、「INITIAL」から取り出した「x」、「y」、「n」を引数としたときの「var」が1となるように式を書けばよいです。

例えば1行3列に8が入ることは最初から分かっているので「var[1][3][8] = 1」となります。これをすべてのINITIALの要素で行います。pulpで記述すると上のようになります。

1つの行に同じ数字は1つ

  # 1つの行に同じ数字は1つ
  for x in NUM:
    for n in NUM:
      problem += pulp.lpSum(var[x][y][n] for y in NUM) == 1

この制約は

「1つの行に同じ数字は1つ」

ということを表しています。数独は1つの行において数字が被るとルール違反になります。

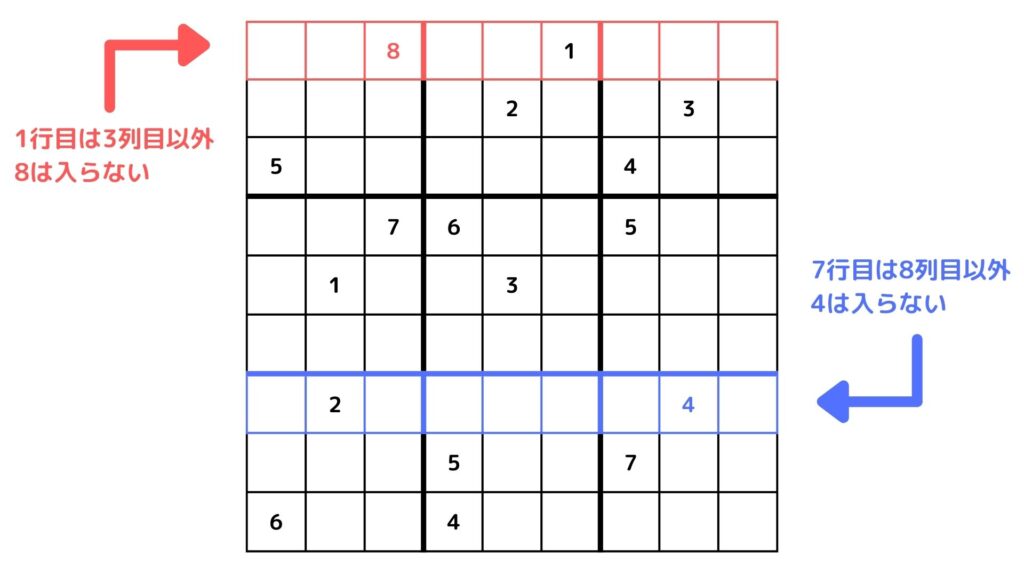
例えば上図を見ると1行目の左から3番目のマスに8が入っていますよね。これを数式で表すと

「var[1][3][8] = 1」

となります。このとき1行目の他のマスに8を入れてはいけないです。これを数式で表すと

「var[1][1][8] = var[1][2][8] = var[1][4][8] = \(\cdots\) = var[1][9][8] = 0」

となります。この2つの式を合わせると

「var[1][1][8] + var[1][2][8] + \(\cdots\) + var[1][9][8] = 1」

となります。他にも例えば7行8列目に4が入っているので、7行目の他の列には8が入りません。これを数式で表すと

「var[7][1][4] + var[7][2][4] + \(\cdots\) + var[7][9][4] = 1」

となります。この制約を全ての行「x」と全ての数字「n」で設定すれば良いです。

1つの列に同じ数字は1つ

  # 1つの列に同じ数字は1つ
  for y in NUM:
    for n in NUM:
      problem += pulp.lpSum(var[x][y][n] for x in NUM) == 1

この制約は

「1つの列に同じ数字は1つ」

ということを表しています。数独は1つの列において数字が被るとルール違反になります。

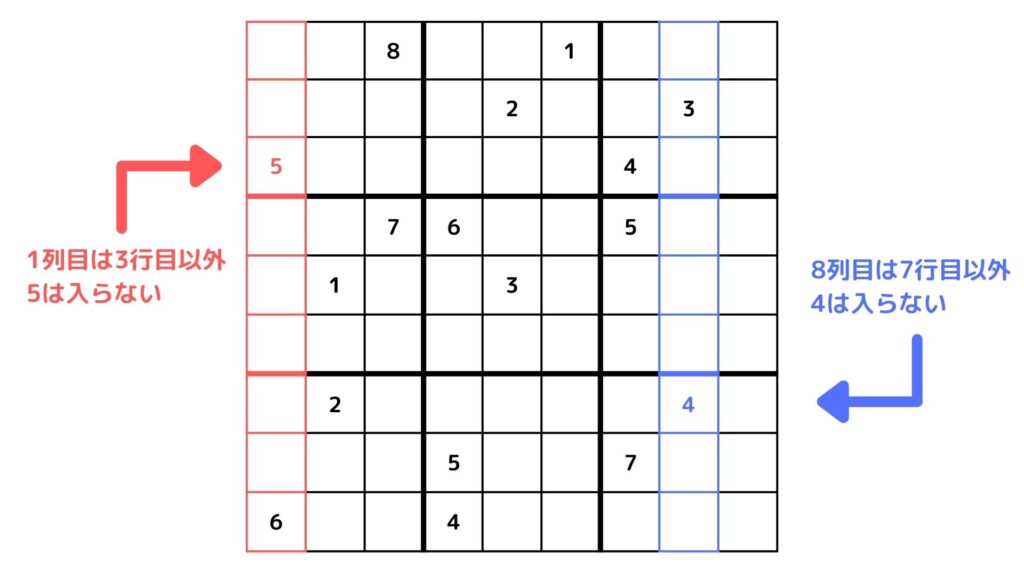
例えば上図を見ると3行1列目のマスに5が入っていますよね。これを数式で表すと

「var[3][1][5] = 1」

となります。このとき1列目の他のマスに5を入れてはいけないです。これを数式で表すと

「var[1][1][5] = var[2][1][5] = var[4][1][5] = \(\cdots\) = var[9][1][5] = 0」

となります。この2つの式を合わせると

「var[1][1][5] + var[2][1][5] + \(\cdots\) + var[9][1][5] = 1」

となります。他にも例えば7行8列目に4が入っているので、8列目の他の行には8が入りません。これを数式で表すと

「var[1][8][4] + var[2][8][4] + \(\cdots\) + var[9][8][4] = 1」

となります。この制約を全ての行「y」と全ての数字「n」で設定すれば良いです。

1つのボックスに同じ数字は1つ

  # １つのボックスに同じ数字は1つ
  for rows in BOX:
    for columns in BOX:
      for n in NUM:
        problem += pulp.lpSum(var[x][y][n] for x in rows for y in columns) == 1

この制約は

「1つのボックスに同じ数字は1つ」

ということを表しています。数独は1つのボックスにおいて数字が被るとルール違反になります。

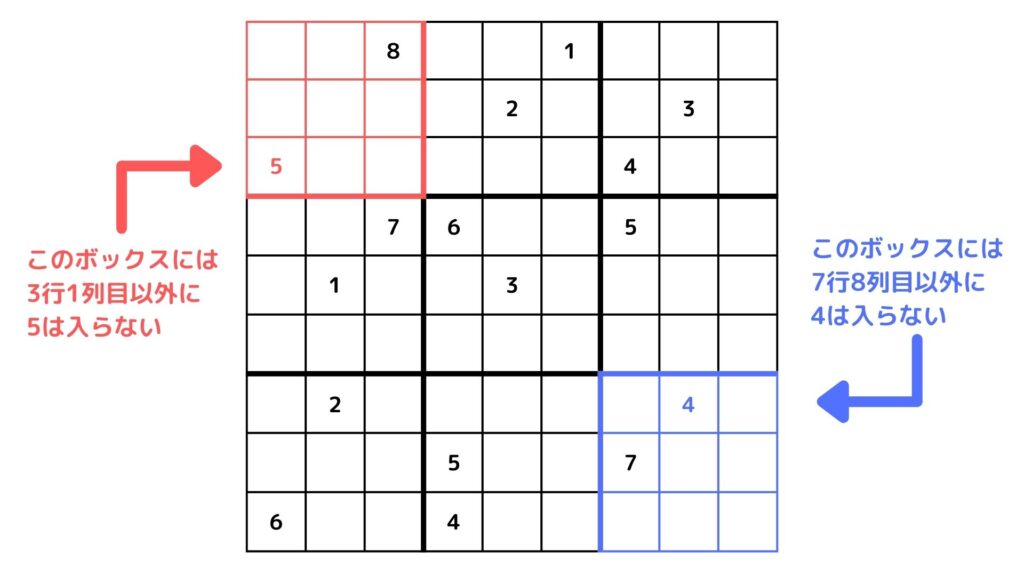
例えば上図を見ると3行1列目のマスに5が入っていますよね。これを数式で表すと

「var[3][1][5] = 1」

となります。このとき左上のボックスの他のマスに5を入れてはいけないです。これを数式で表すと

var[1][1][5] = var[1][2][5] = var[1][3][5] = 0
var[2][1][5] = var[2][2][5] = var[2][3][5] = 0
var[3][2][5] = var[3][3][5] = 0

となります。この2つの式を合わせると

「var[1][1][5] + var[1][2][5] + \(\cdots\) + var[3][3][5] = 1」

となります。この条件を記述するにはは少し工夫が必要です。例えば左上のボックスについて考えるときは「x」、「y」がそれぞれ1～3を取りうるの場合を考えます。他には例えば右下のボックスについて考えるときはxが7～9、yが7～9を取りうるの場合を考えます。

すべてのボックスを考えるためには上のコードの2～3行目のように[[1,2,3], [4,5,6], [7,8,9]]の2次元リストをfor文で2度回せばOKです。

例えば「row = [1,2,3]」、「column = [1,2,3]」のときは左上のボックスを表し、「row = [7,8,9]」、「column = [1,2,3]」のときは左下のボックスを表します。

そして各ボックスにおいてfor文でnを回して「n = 1」、「n = 2」、…、「n = 9」の場合でさきほどの条件を書けば制約条件が出来上がります。

上記のことを実現するためには事前準備で用意したBOXという二次元リストを使えばOKです。

問題を解く

  # 問題を解く
  result = problem.solve()
  # 結果を格納する空の9×9の二次元リストを作成
  result_list =[[] for i in range(9)]
  # 変数の値が1のものをresult_listに追加
  for x in NUM:
    for y in NUM:
      for n in NUM:
        if pulp.value(var[x][y][n]) == 1:
          result_list[x-1].append(n)

  return result_list

このコードでは、さきほどまで設定していた整数計画問題を解いて結果を出力しています。

2行目で問題を解いています。結果は「result」としています。

4行目で出力結果を格納する2次元リストを作成しています。リストの名前は「result_list」としています。

6～10行目で変数の値が1のものだけ取り出して「result_list」の要素として追加しています。

例えば「var[3][1][4] = 1」のときは「result_list[2]」のリストに4を追加しています。

12行目で「result_list」を返しています。

問題を解く

## 問題を解く
# 初期値を設定する
INITIAL = [[1,3,8],[1,6,1],
           [2,5,2],[2,8,3],
           [3,1,5],[3,7,4],
           [4,3,7],[4,4,6],[4,7,5],
           [5,2,1],[5,5,3],
           [7,2,2],[7,8,1],
           [8,4,5],[8,7,7],
           [9,1,6],[9,4,4]]
# 解を取得する
ans = sudoku(INITIAL)
# 解を表示する
for row in ans:
    print(row)

この部分では今定義した関数「sudoku」を使って実際に問題を解いています。

3～10行目ではすでに分かっているマスの情報を表す「INITIAL」を定義しています。例えば「[1,3,8]」が要素としてありますがこれは

1行3列目には8が入る

ことを表しています。

12行目では関数「sudoku」に「INITIAL」を入力して解を取得しています。解は「ans」と名前を付けました。

14～15行目ではfor文を使って1行ずつ解を出力しています。出力結果は下図のようになりました。