- 論理演算ってなに?
- ANDとかORとかの論理演算をパーセプトロンで表現したい…
- XORはパーセプトロンで表現できないの?
こんにちは!しゅんです!
今回は論理演算をパーセプトロンで表現する方法について解説していきます!またpythonでの実装方法についても解説します!
それではやっていきましょう!
普段は組合せ最適化の記事を書いてたりします。
ぜひ他の記事も読んでみてください!
このブログの簡単な紹介はこちらに書いてあります。
興味があったら見てみてください。
このブログでは経営工学を勉強している現役理系大学生が、経営工学に関することを色々話していきます!
ぼくが経営工学を勉強している中で感じたことや、興味深かったことを皆さんと共有出来たら良いなと思っています。
そもそも経営工学とは何なのでしょうか。Wikipediaによると
経営工学(けいえいこうがく、英: engineering management)は、人・材料・装置・情報・エネルギーを総合したシステムの設計・改善・確立に関する活動である。そのシステムから得られる結果を明示し、予測し、評価するために、工学的な分析・設計の原理・方法とともに、数学、物理および社会科学の専門知識と経験を利用する。
引用元 : 経営工学 – Wikipedia
長々と書いてありますが、要は経営、経済の課題を理系的な観点から解決する学問です。
論理演算ってなに?
論理演算とは0か1しか取らない変数\(x_1,x_2\)を使って行う演算のことです。と説明されてもよく分からないので具体例を使って説明していきます。
この記事では変数が\(x_1,x_2\)の2つの場合の説明をしますが、変数が3個でも4個でも100個でも論理演算を考えることができます。
AND(論理積)
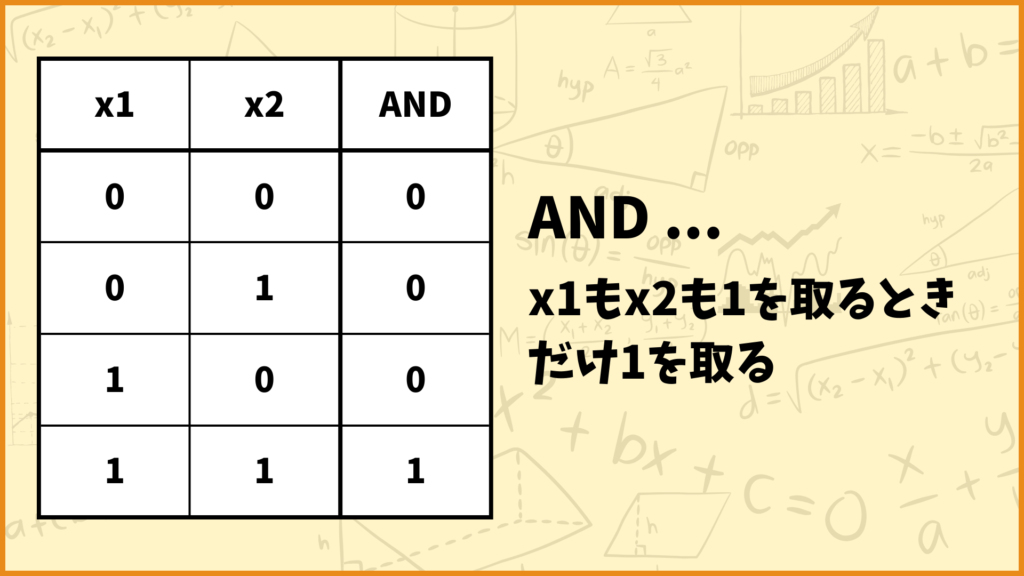
論理演算としてAND(論理積)というものがあります。これは\(x_1,x_2\)が両方1を取るときだけ1を取り、それ以外は0を取る論理演算です。
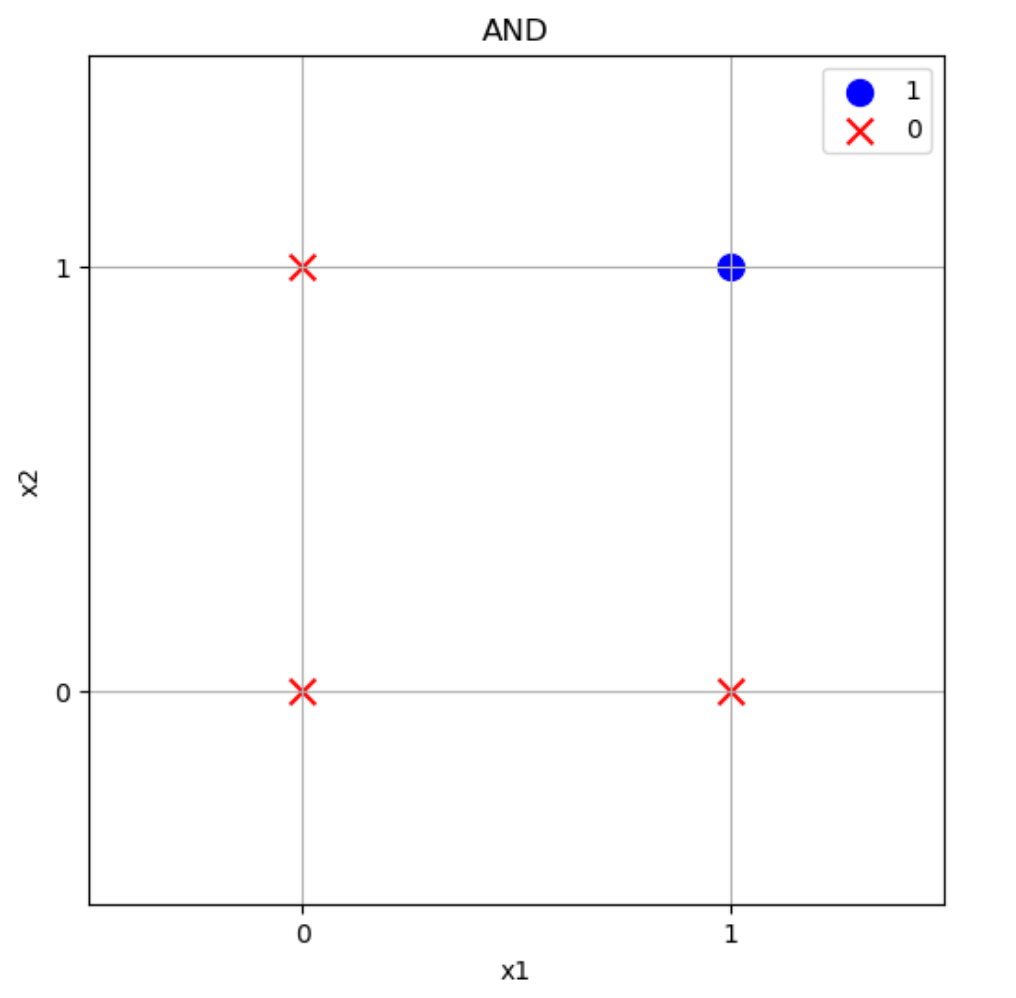
グラフにすると上のような感じです。\((x_1,x_2)=(1,1)\)のときだけ1で青〇になっていますが、それ以外のときは0で赤×になっています。
OR(論理和)

論理演算としてOR(論理和)というものがあります。これは\(x_1,x_2\)のどちらかが1を取るときに1を取り、両方とも0のときだけ0を取る論理演算です。
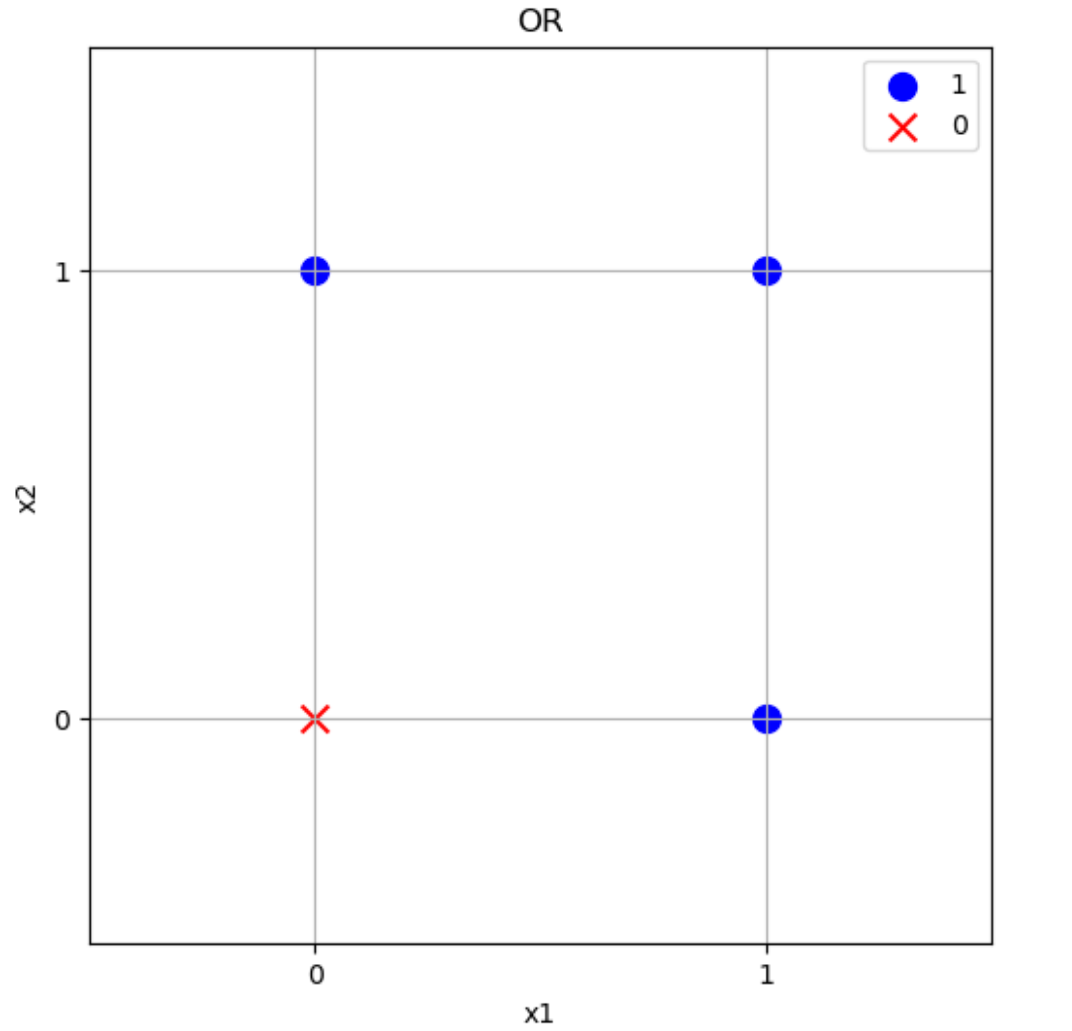
グラフにすると上のような感じです。\(x_1=1\)または\(x_2=1\)のとき1で青〇になっていますが、\((x_1,x_2)=(0,0)\)のときだけ0で赤×になっています。
XOR(排他的論理和)

論理演算としてXOR(排他的論理和)というものがあります。これは\(x_1,x_2\)が異なる値を取るときに1を取り、同じ値を取るときに0を取ります。
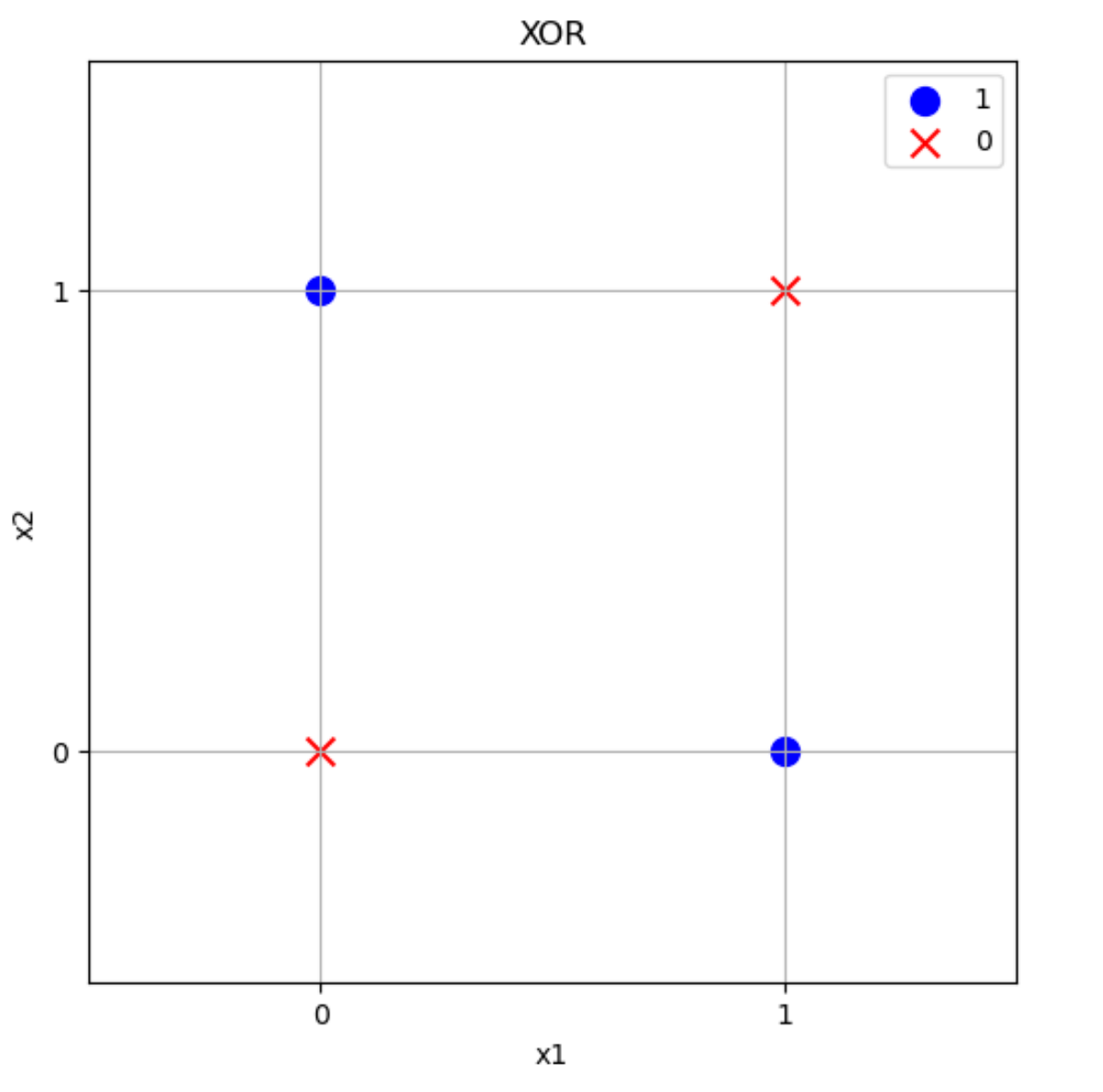
グラフにすると上のような感じです。\((x_1,x_2)=(1,0)\)または\((x_1,x_2)=(0,1)\)のとき1で青〇になっていますが、\((x_1,x_2)=(0,0)\)のときまたは\((x_1,x_2)=(1,1)\)のとき0で赤×になっています。
\\\ 排他的論理和の詳しい説明はこちらから! ///
2変数の論理演算は16種類ある
ここまでAND,OR,XORの3種類の論理演算を見てきましたが、他にも論理演算は存在します。

\((x_1,x_2)=(0,0)\)のときの演算結果は0か1を取るので2通りあります。
\((x_1,x_2)=(0,1)\)のときの演算結果は0か1を取るので2通りあります。
\((x_1,x_2)=(1,0)\)のときの演算結果は0か1を取るので2通りあります。
\((x_1,x_2)=(1,1)\)のときの演算結果は0か1を取るので2通りあります。
ということで合計\(2\times2\times2\times2=16\)通りの論理演算が存在します。AND,OR,XORはその中の3つだったということです。

例えば上の論理演算は、\((x_1,x_2)=(0,0)\)のときだけ1を取り、それ以外は0を取るような演算です。この演算結果とORの演算結果を見比べると、1と0が全部逆になっていることが分かります。
この論理演算はORの否定なのでNORと言ったりします。

例えば上の論理演算は、\((x_1,x_2)=(1,1)\)のときだけ0を取り、それ以外は1を取るような演算です。この演算結果とANDの演算結果を見比べると、1と0が全部逆になっていることが分かります。
この論理演算はORの否定なのでNANDと言ったりします。
パーセプトロンってなに?
ここでは2変数の論理演算をパーセプトロンで表現することに関係する内容を中心に説明します。パーセプトロンのより詳しい説明は別の記事でしているので、気になる方はぜひそちらも見てみてください!
\\\ パーセプトロンの詳しい解説はこちらから! ///
入力が2つの場合のパーセプトロン
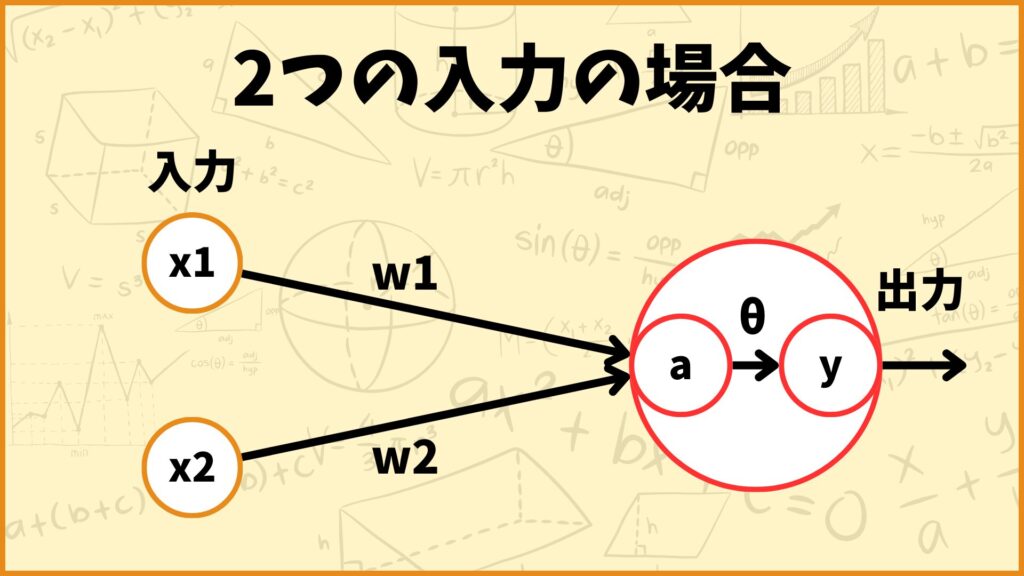
例えば\(x_1,x_2\)の2つがパーセプトロンに入力されたとします。このときパーセプトロンではこの2つの入力に、自分で設定した重み\(w_1,w_2\)を掛け算して足します。
この計算で得られたものを\(a\)とすると
\(a = w_1x_1+w_2x_2\)
となります。例えば\((x_1,x_2)=(1,2)\)が入力され、重みを\((w_1,w_2)=(3,4)\)と設定したとき
\(a = 3\times1+4\times2=11\)
と計算できます。そしてこの\(a\)が、自分で設定する\(\theta\)より大きかったら1、そうでなかったら0を返すのがパーセプトロンです。例えば\(a=11\)で\(\theta = 8\)と設定したとき
\(a = 11 > 8 = \theta\)
となるのでパーセプトロンは1を返します。
\( a = w_1x_1 + w_2x_2\)なので
\( w_1x_1+w_2x_2 > \theta \; \to 1\text{を返す}\)
\( w_1x_1+w_2x_2 \leq \theta \; \to 0\text{を返す}\)
となります。ここで\(\theta\)を右辺に移項すると
\( w_1x_1+w_2x_2-\theta > 0 \; \to 1\text{を返す}\)
\( w_1x_1+w_2x_2-\theta \leq 0 \; \to 0\text{を返す}\)
となります。さらに\(-\theta = b\)とすると
\( w_1x_1+w_2x_2+b > 0 \; \to 1\text{を返す}\)
\( w_1x_1+w_2x_2+b \leq 0 \; \to 0\text{を返す}\)
となります。ここで登場する\(b\)はバイアスと呼ばれます。この後pythonで実装するときは\(\theta\)ではなく\(b\)を使って実装していきます。
パーセプトロンは直線で領域を2つに分離できる
例えば重みを\((w_1,w_2) = (3,4)\)、バイアスを\(b=-5\)と設定したとします。このとき
\(w_1+x_1+w_2x_2+b = 3x_1+4x_2-5\)
となります。これを\(x_1-x_2\)平面上で描くと下図のようになります。
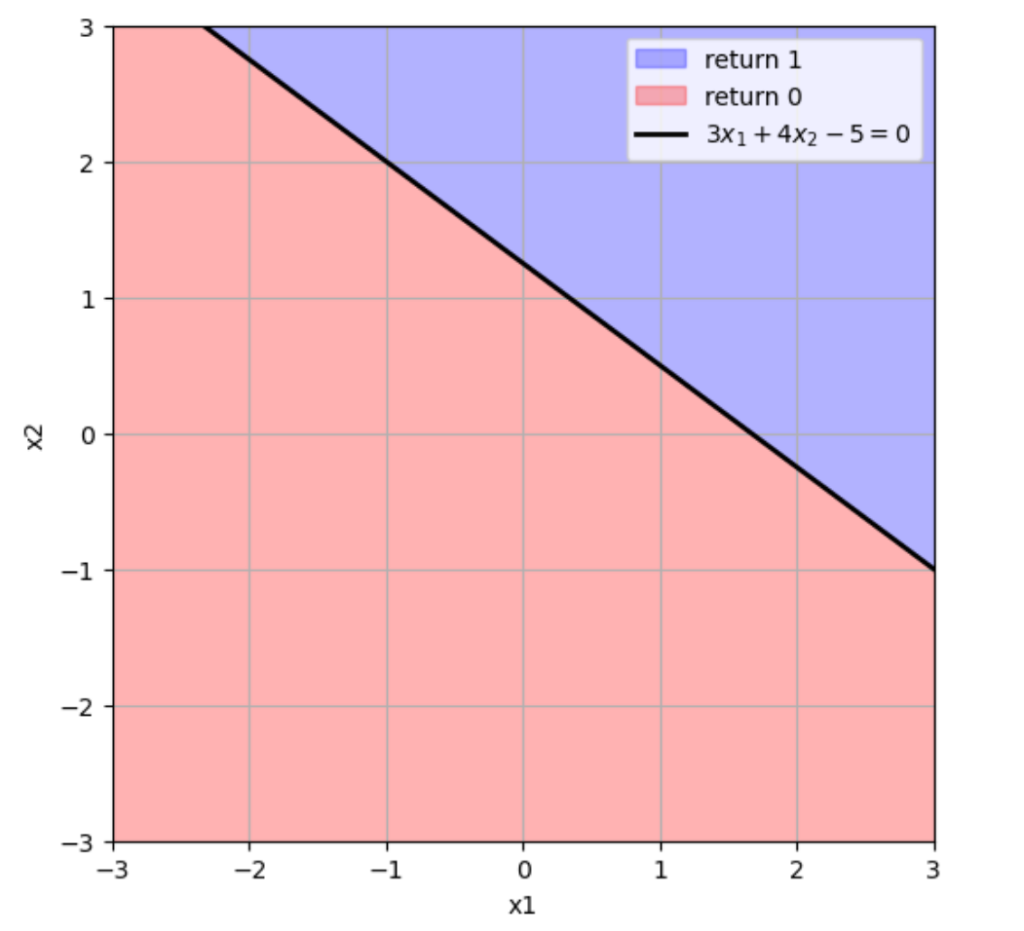
図の黒い直線が\(3x_1+4x_2-5=0\)を表していて、青い領域、赤い領域がそれぞれ
(青い領域)\(3x_1+4x_2-5>0\)
(赤い領域)\(3x_1+4x_2-5\leq0\)
を表しています。パーセプトロンは\(3x_1+4x_2-5>0\)なら1を返し、\(3x_1+4x_2-5\leq0\)なら0を返すので、図の青い領域内の\((x_1,x_2)\)(例えば\((x_1,x_2)=(2,1)\))をパーセプトロンに入力すれば1を返し、赤い領域内の\((x_1,x_2)\)(例えば\((x_1,x_2)=(0,0)\))をパーセプトロンに入力すれば0を返します。
つまりパーセプトロンは直線を境界として1を返すか0を返すかで領域を2つに分離することができるんです。
論理演算の結果を直線で分離できるか考える
今回の目的はAND,ORなどの論理演算をパーセプトロンで表現できるか考えることですが、結論これは論理演算の結果を直線で分離できるかを考えることと同じになります。
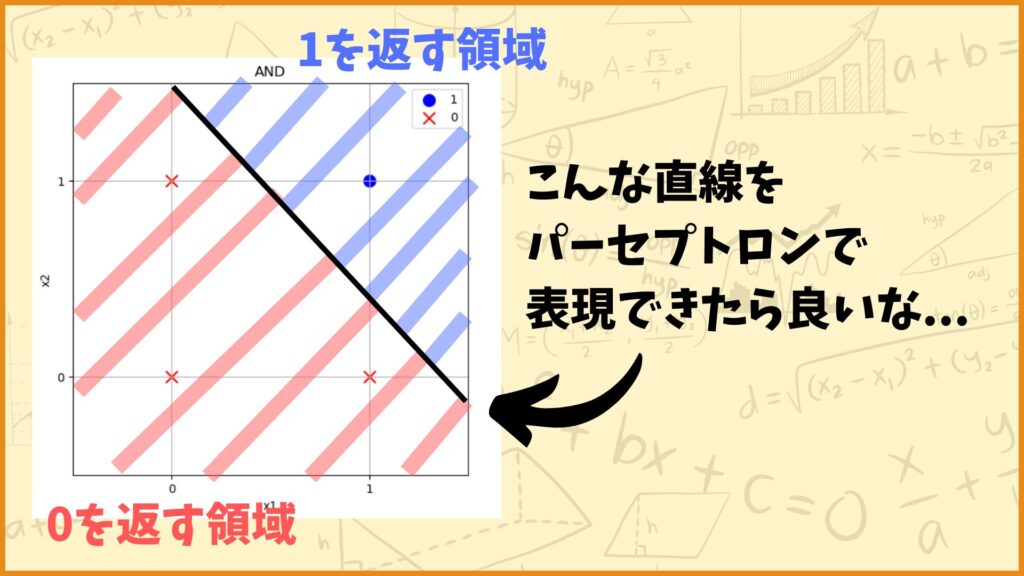
上図はANDを図示したものになります。ANDは\((x_1,x_2)=(1,1)\)のときだけ1を返し、それ以外は0を返しますが、例えば上図のような直線をパーセプトロンで表現することができたらANDを表現することができます。
つまり\((x_1,x_2)=(1,1)\)は青い領域に属し、それ以外の3点は赤い領域に属すような重み\(w_1,w_2\)とバイアス\(b\)を決定することができたら、ANDをパーセプトロンで表現できるというわけです。
他の論理演算も「演算結果を分離できるように重みとバイアスを設定できるか」という風に考えていきます。
まとめ:
論理演算をパーセプトロンで表現するために「論理演算の結果を分離できるように重みとバイアスを設定できるか」を考える。
論理演算をパーセプトロンで表現したい
それでは実際に論理演算をパーセプトロンで表現していきましょう。まずはANDとORを表現してみましょう。
ANDをパーセプトロンで表現する

先ほど説明したように、ANDをパーセプトロンで実装するためには上図のような直線を表現できれば良いです。例えば
\((w_1,w_2)=(5,5),b=-7\)とすると、直線の方程式は
\(w_1x_1+w_2x_2+b=0 \to 5x_1+5x_2-7=0\)
となります。上図の4点をそれぞれ入力してみると
\((x_1,x_2)=(0,0) : 5\times0+5\times0-7=-7\leq0 \to 0\text{を返す}\)
\((x_1,x_2)=(1,0) : 5\times1+5\times0-7=-2\leq0 \to 0\text{を返す}\)
\((x_1,x_2)=(0,1) : 5\times0+5\times1-7=-2\leq0 \to 0\text{を返す}\)
\((x_1,x_2)=(1,1) : 5\times1+5\times1-7=3>0 \to 1\text{を返す}\)
となり、ANDを実装できています。\((w_1,w_2)=(5,5),b=-7\)のときの境界をグラフにすると下図のようになります。
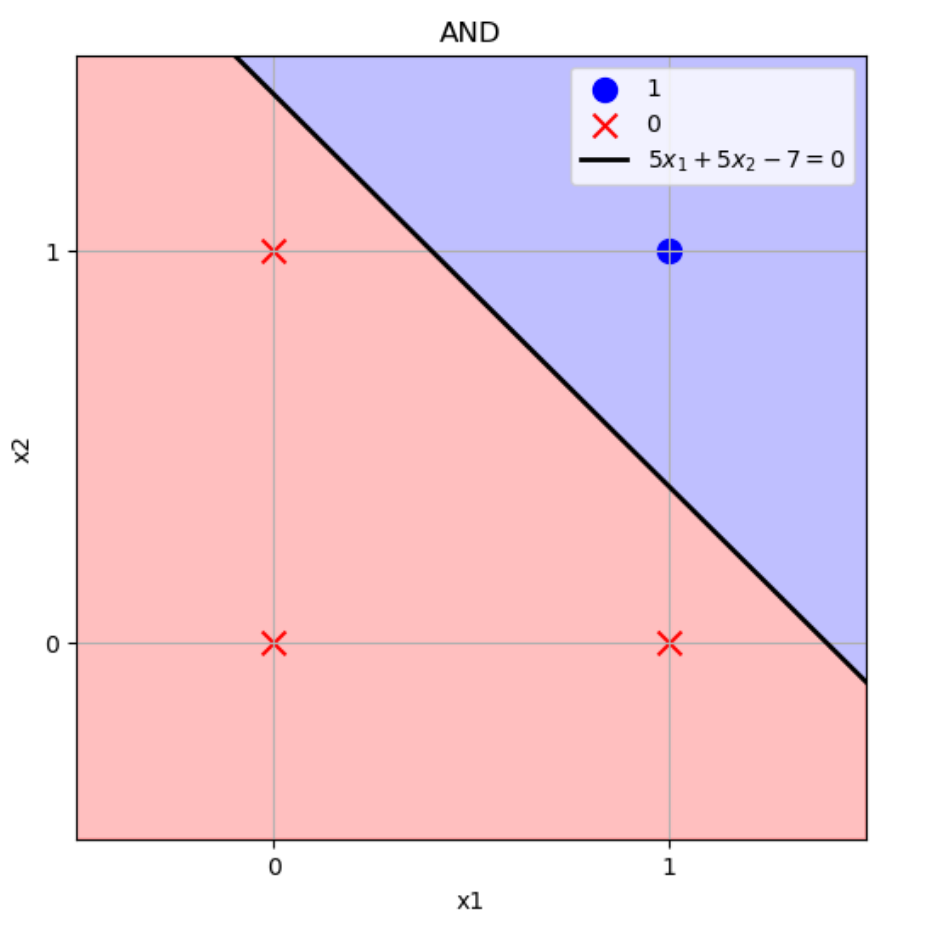
この直線より上側の点をパーセプトロンに入力したら1を返し、下側の点をパーセプトロンに入力したら0を返します。
他にも例えば
\((w_1,w_2)=(3,7),b=-8\)とすると、直線の方程式は
\(w_1x_1+w_2x_2+b=0 \to 3x_1+7x_2-8=0\)
となります。上図の4点をそれぞれ入力してみると
\((x_1,x_2)=(0,0) : 3\times0+7\times0-8=-8\leq0 \to 0\text{を返す}\)
\((x_1,x_2)=(1,0) : 3\times1+7\times0-8=-5\leq0 \to 0\text{を返す}\)
\((x_1,x_2)=(0,1) : 3\times0+7\times1-8=-1\leq0 \to 0\text{を返す}\)
\((x_1,x_2)=(1,1) : 3\times1+7\times1-8=2>0 \to 1\text{を返す}\)
となり、ANDを実装できています。\((w_1,w_2)=(3,7),b=-8\)のときの境界をグラフにすると下図のようになります。
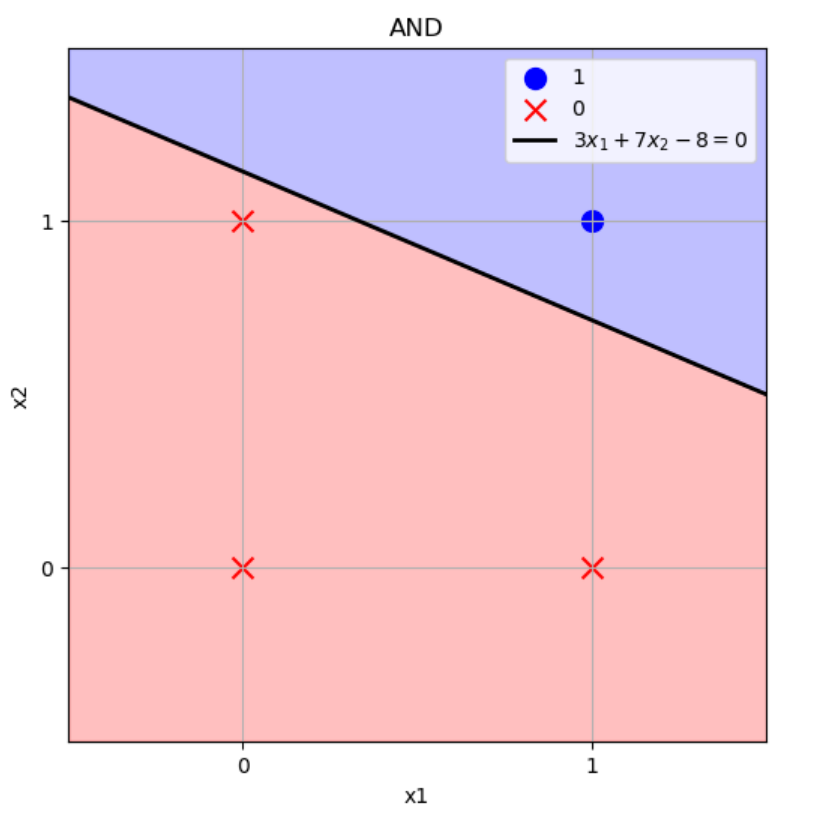
この直線より上側の点をパーセプトロンに入力したら1を返し、下側の点をパーセプトロンに入力したら0を返します。
上図の例を見たら分かるように、ANDを表現できるパーセプトロンの重みとバイアスの組合せは無限に存在します。
ORをパーセプトロンで表現する

ORをパーセプトロンで実装するためには上図のような直線を表現できれば良いです。例えば
\((w_1,w_2)=(5,5),b=-2\)とすると、直線の方程式は
\(w_1x_1+w_2x_2+b=0 \to 5x_1+5x_2-2=0\)
となります。上図の4点をそれぞれ入力してみると
\((x_1,x_2)=(0,0) : 5\times0+5\times0-2=-2\leq0 \to 0\text{を返す}\)
\((x_1,x_2)=(1,0) : 5\times1+5\times0-2=3>0 \to 1\text{を返す}\)
\((x_1,x_2)=(0,1) : 5\times0+5\times1-2=3\>0 \to 1\text{を返す}\)
\((x_1,x_2)=(1,1) : 5\times1+5\times1-2=8>0 \to 1\text{を返す}\)
となり、ORを実装できています。\((w_1,w_2)=(5,5),b=-2\)のときの境界をグラフにすると下図のようになります。
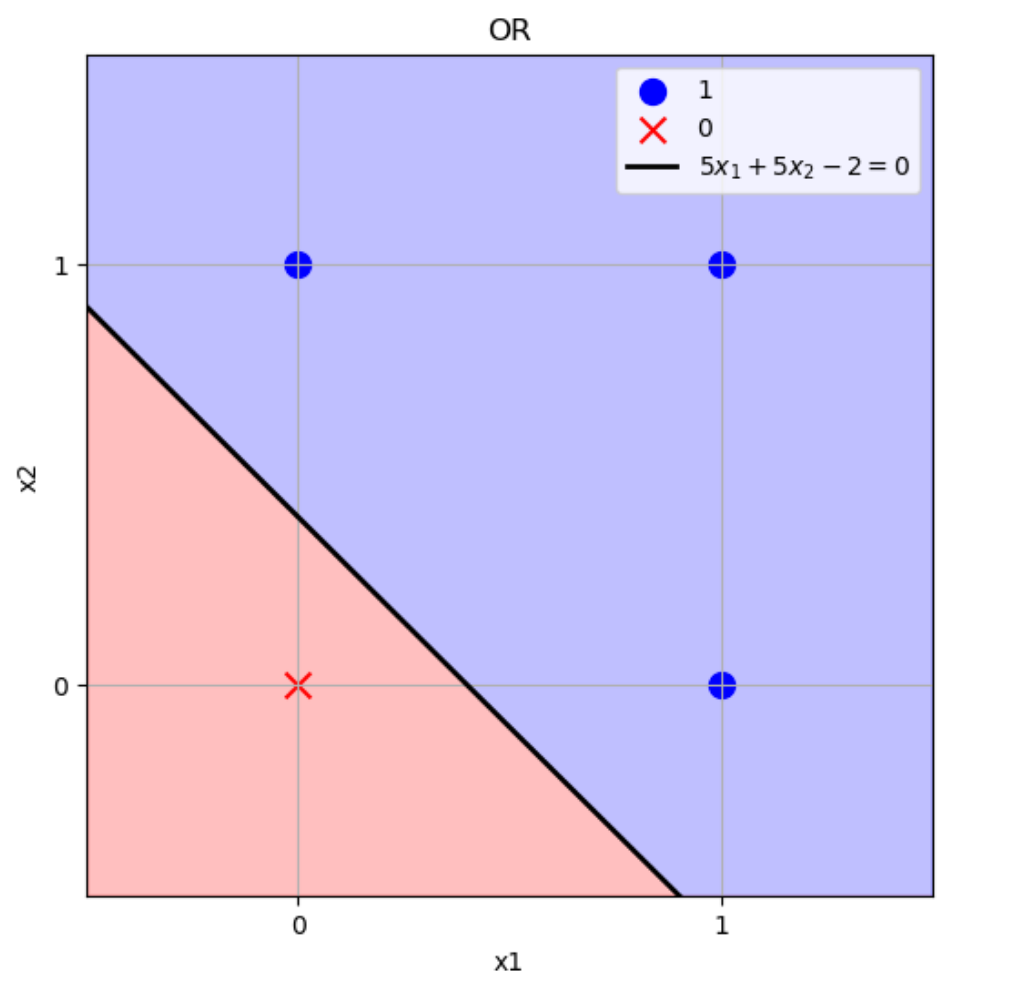
この直線より上側の点をパーセプトロンに入力したら1を返し、下側の点をパーセプトロンに入力したら0を返します。
他にも例えば
\((w_1,w_2)=(2,6),b=-1\)とすると、直線の方程式は
\(w_1x_1+w_2x_2+b=0 \to 2x_1+6x_2-1=0\)
となります。上図の4点をそれぞれ入力してみると
\((x_1,x_2)=(0,0) : 2\times0+6\times0-1=-1\leq0 \to 0\text{を返す}\)
\((x_1,x_2)=(1,0) : 2\times1+6\times0-1=1\leq0 \to 1\text{を返す}\)
\((x_1,x_2)=(0,1) : 2\times0+6\times1-1=5\leq0 \to 1\text{を返す}\)
\((x_1,x_2)=(1,1) : 2\times1+6\times1-1=7>0 \to 1\text{を返す}\)
となり、ANDを実装できています。\((w_1,w_2)=(2,6),b=–1\)のときの境界をグラフにすると下図のようになります。
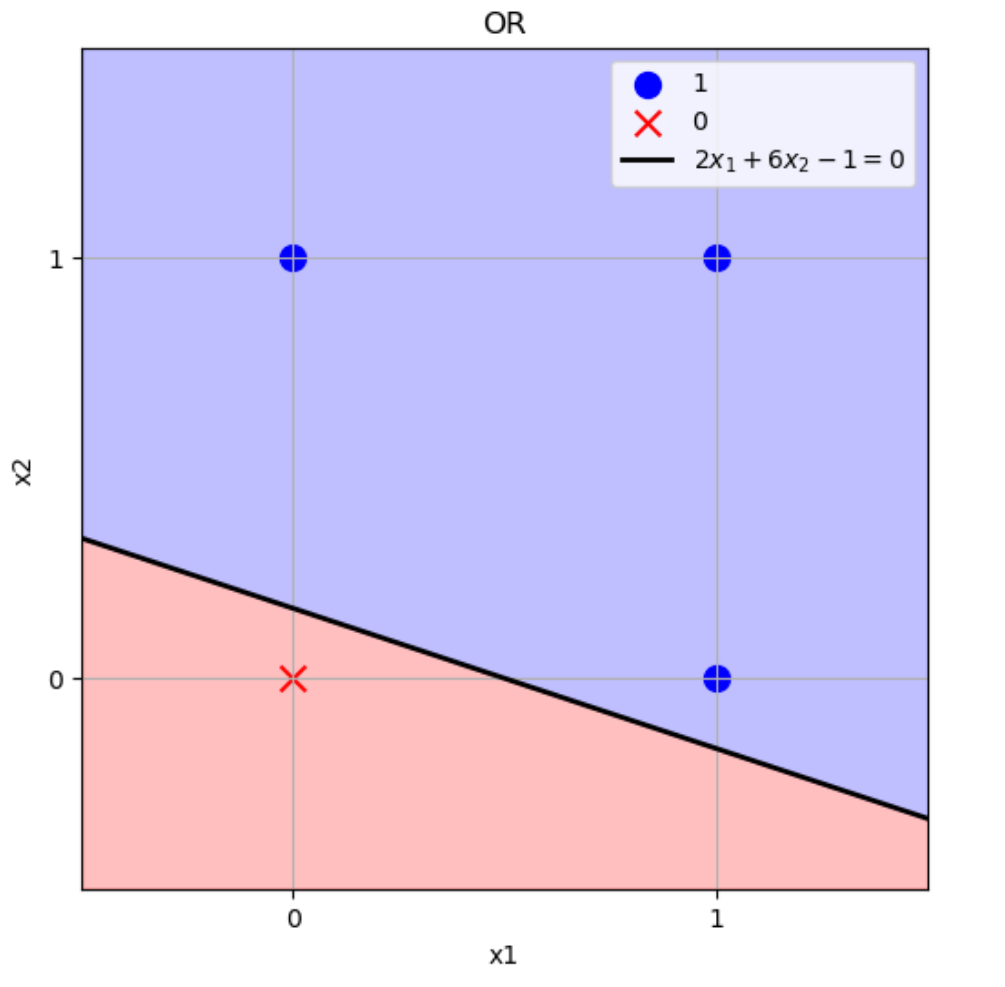
この直線より上側の点をパーセプトロンに入力したら1を返し、下側の点をパーセプトロンに入力したら0を返します。
上図の例を見たら分かるように、ORを表現できるパーセプトロンの重みとバイアスの組合せは無限に存在します。
パーセプトロンで表現できない論理演算があるの?
実は論理演算の中にはパーセプトロンで表現することができないものがあります。パーセプトロンで計算ができない論理演算の特徴は
演算結果を直線で分離できないもの
です。例えばXORはパーセプトロンで表現できない論理演算です。ということでここではパーセプトロンで表現できない論理演算について考えてみましょう。
XORはパーセプトロンで表現できない
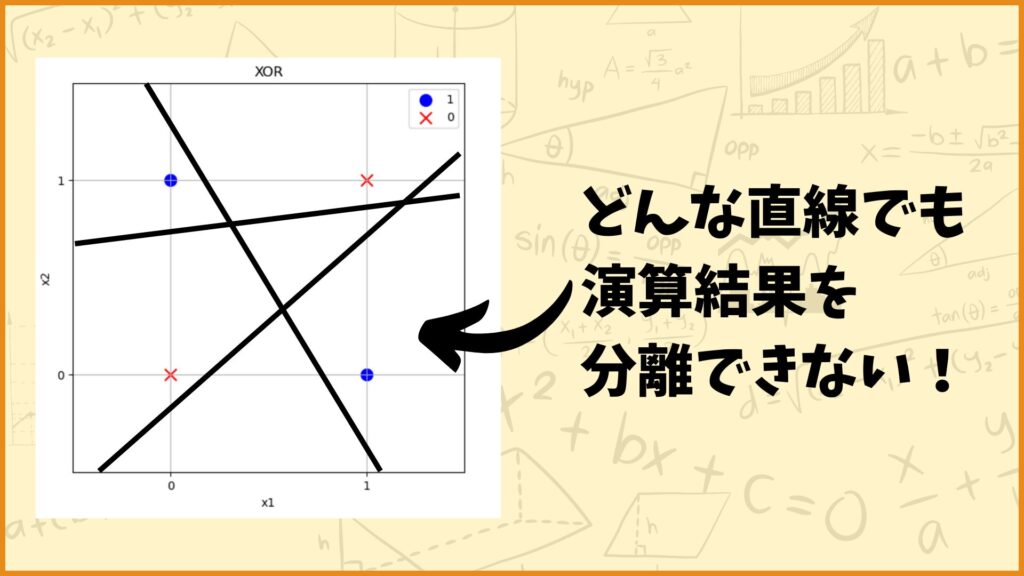
XORの演算結果を考えてみると、どんな直線でも演算結果を分離することができないことが分かります。もしXORの演算結果を分離したかったら下図のような曲線で分離する必要があります。
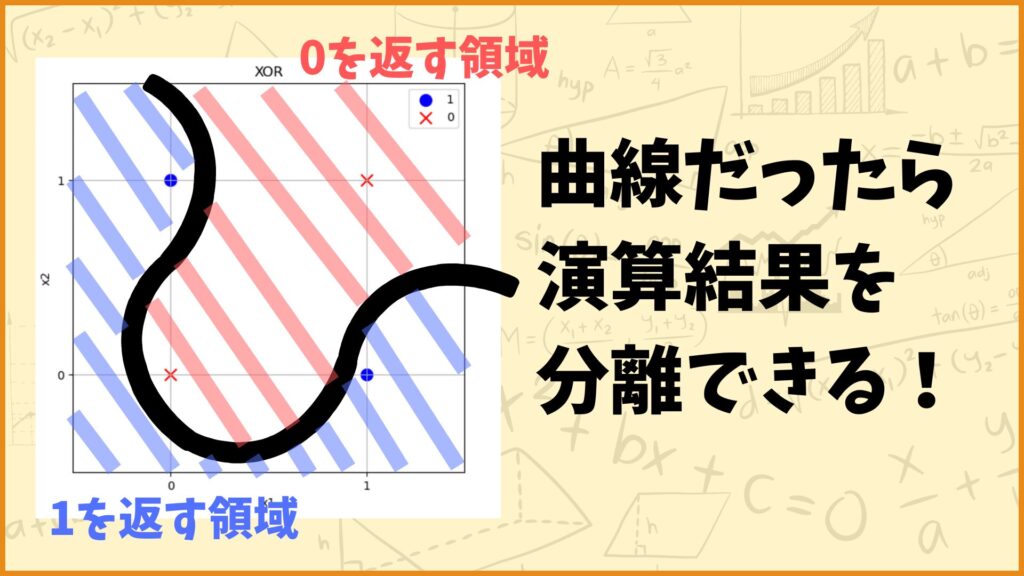
しかし(単純)パーセプトロンは直線での分離しかできないので、上図のような曲線をパーセプトロンで表現することはできません。
数式を使ってパーセプトロンでXORを表現することができないことを確かめてみましょう。今重みを\((w_1,w_2)\)、バイアスを\(b\)とします。XORは\((x_1,x_2)\)を入力したときの出力値がそれぞれ
\((x_1,x_2)=(0,0) \to 0\text{を出力}\)
\((x_1,x_2)=(1,0) \to 1\text{を出力}\)
\((x_1,x_2)=(0,1) \to 1\text{を出力}\)
\((x_1,x_2)=(1,1) \to 0\text{を出力}\)
となります。またパーセプトロンの出力値は
\(w_1x_1+w_2x_2+b >0 \to 1\text{を出力}\)
\(w_1x_1+w_2x_2+b \leq0 \to 0\text{を出力}\)
となります。従ってXORをパーセプトロンで表現するためには
\((x_1,x_2)=(0,0) \to w_1\times0+w_2\times0+b=b\leq0\)
\((x_1,x_2)=(1,0) \to w_1\times1+w_2\times0+b=w_1+b>0\)
\((x_1,x_2)=(0,1) \to w_1\times0+w_2\times1+b=w_2+b>0\)
\((x_1,x_2)=(1,1) \to w_1\times1+w_2\times1+b=w_1+w_2+b\leq0\)
の4つの不等式を満たす\(w_1,w_2,b\)を見つける必要があります。2つ目の式の\(w_1+b>0\)より\(w_1>-b\)、3つ目の式の\(w_2+b>0\)より\(w_2>-b\)が成立します。よって4つ目の式は
\(0\geq w_1+w_2+b>-b-b+b=-b\)
となるので\(b>0\)が成立する必要があります。一方で1つ目の式から\(b\leq0\)が成り立つ必要があり、この2つの式を同時に満たす\(b\)は存在しません。
以上のことからXORをパーセプトロンで表現できないことが示せました。
その他の論理演算はどうなの?
それでは今紹介したAND,OR,XOR以外の論理演算がパーセプトロンで表現できるのかどうかを考えてみましょう。先ほども述べたように入力が2変数のとき論理演算は16種類あるので、残りの13種類について見ていきましょう。
なお\((x_1,x_2)=(0,0)\)を入力したときの出力値を\(\alpha_1\)、\((x_1,x_2)=(1,0)\)を入力したときの出力値を\(\alpha_2\)、\((x_1,x_2)=(0,1)\)を入力したときの出力値を\(\alpha_3\)、\((x_1,x_2)=(1,1)\)を入力したときの出力値を\(\alpha_4\)と表記して論理演算を表したいと思います。
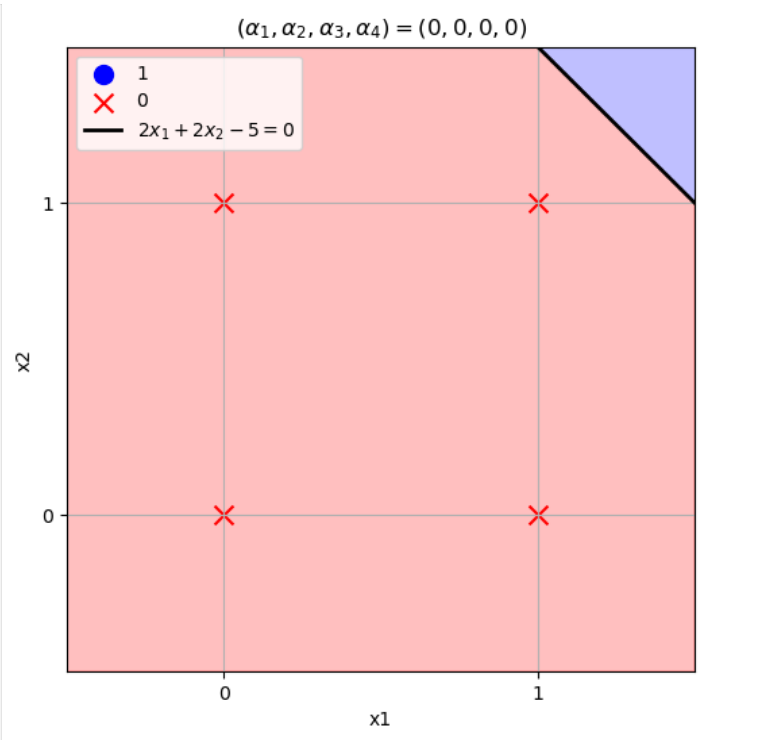
\((w_1,w_2)=(2,2),b=-5\)のとき
\((x_1,x_2)=(0,0) \to w_1x_1+w_2x_2+b=2\times0+2\times0-5=-5\leq0\)
\((x_1,x_2)=(1,0) \to w_1x_1+w_2x_2+b=2\times1+2\times0-5=-3\leq0\)
\((x_1,x_2)=(0,1) \to w_1x_1+w_2x_2+b=2\times0+2\times1-5=-3\leq0\)
\((x_1,x_2)=(1,1) \to w_1x_1+w_2x_2+b=2\times1+2\times1-5=-1\leq0\)
となりこの論理演算を表現できる。
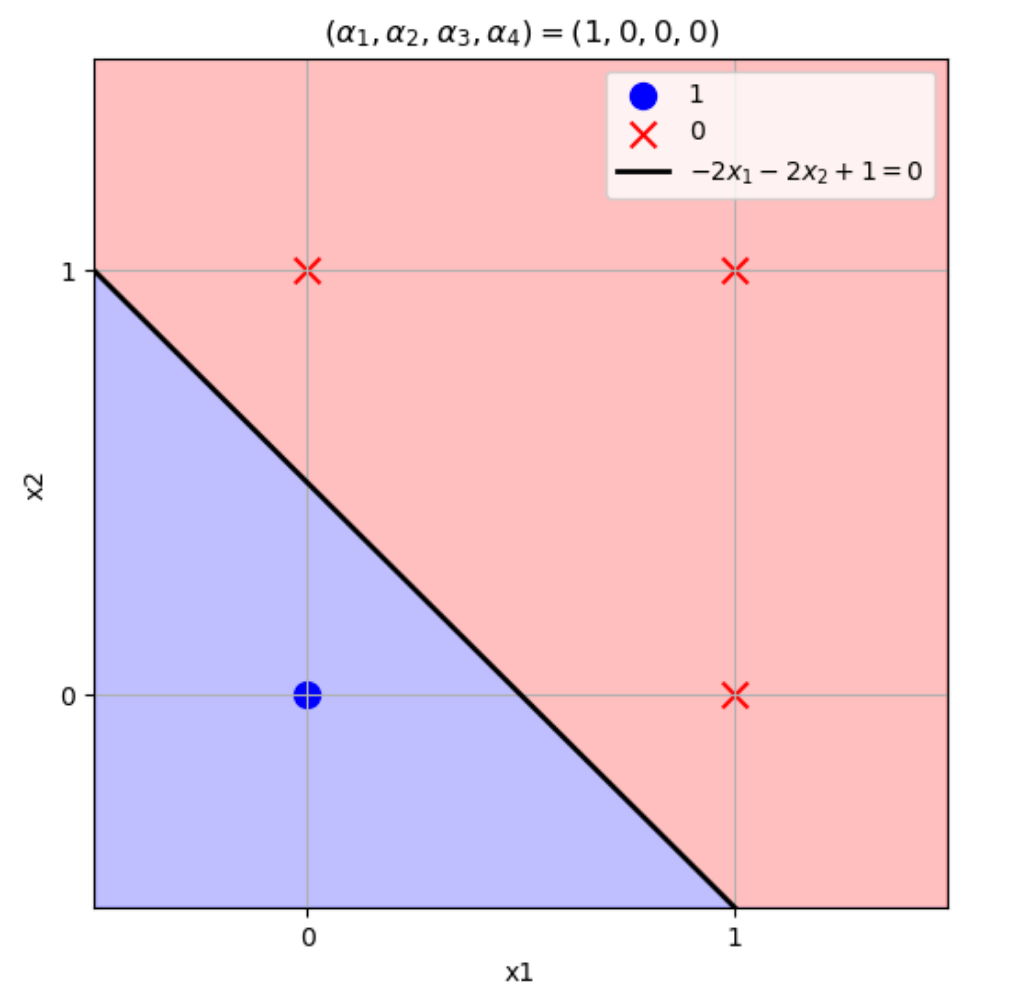
\((w_1,w_2)=(-2,-2),b=1\)のとき
\((x_1,x_2)=(0,0) \to w_1x_1+w_2x_2+b=-2\times0-2\times0+1=1>0\)
\((x_1,x_2)=(1,0) \to w_1x_1+w_2x_2+b=-2\times1-2\times0+1=-1\leq0\)
\((x_1,x_2)=(0,1) \to w_1x_1+w_2x_2+b=-2\times0-2\times1+1=-1\leq0\)
\((x_1,x_2)=(1,1) \to w_1x_1+w_2x_2+b=-2\times1-2\times1+1=-3\leq0\)
となりこの論理演算を表現できる。
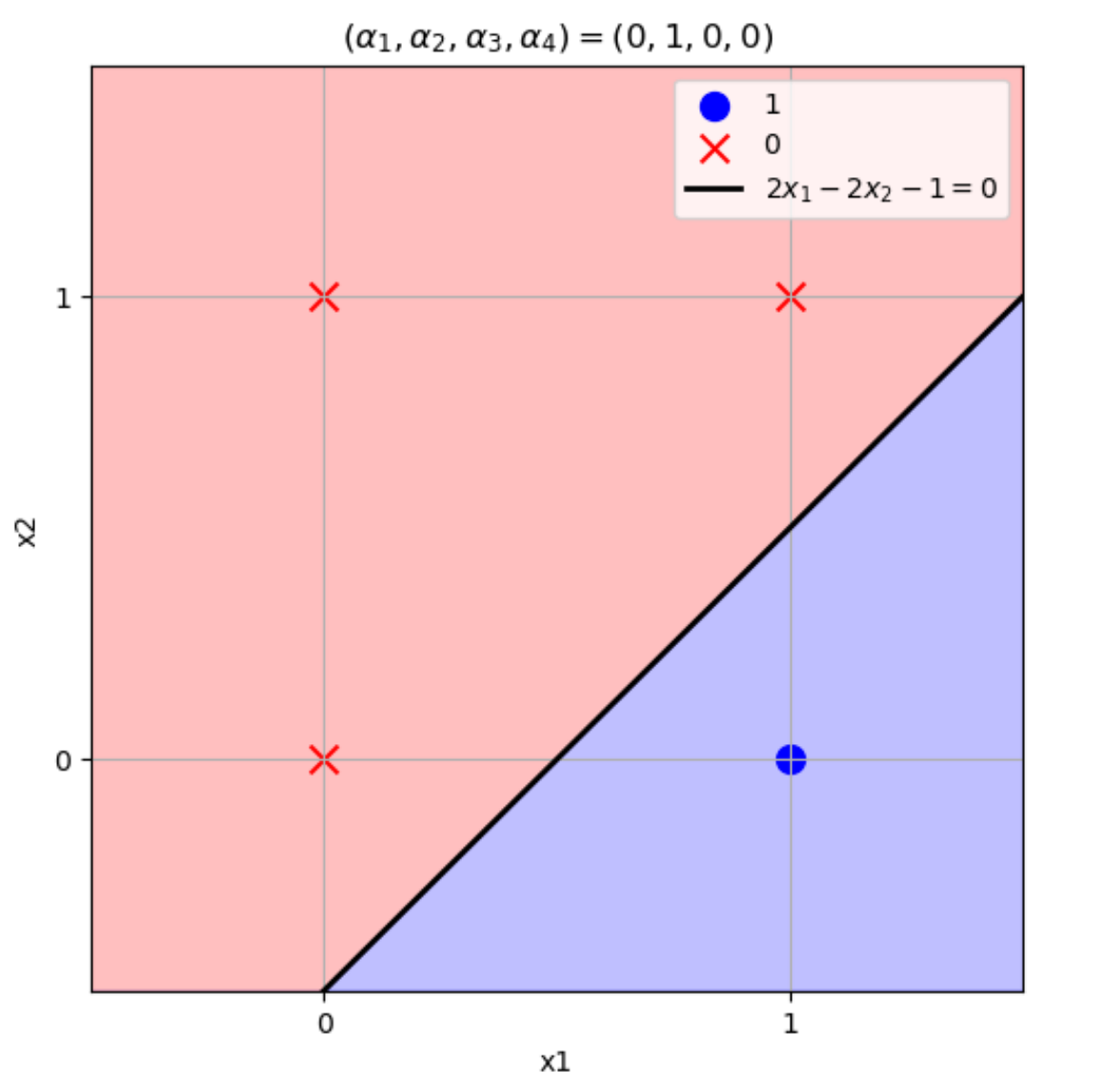
\((w_1,w_2)=(2,-2),b=-1\)のとき
\((x_1,x_2)=(0,0) \to w_1x_1+w_2x_2+b=2\times0-2\times0-1=-1\leq0\)
\((x_1,x_2)=(1,0) \to w_1x_1+w_2x_2+b=2\times1-2\times0-1=1>0\)
\((x_1,x_2)=(0,1) \to w_1x_1+w_2x_2+b=2\times0-2\times1-1=-3\leq0\)
\((x_1,x_2)=(1,1) \to w_1x_1+w_2x_2+b=2\times1-2\times1-1=-1\leq0\)
となりこの論理演算を表現できる。
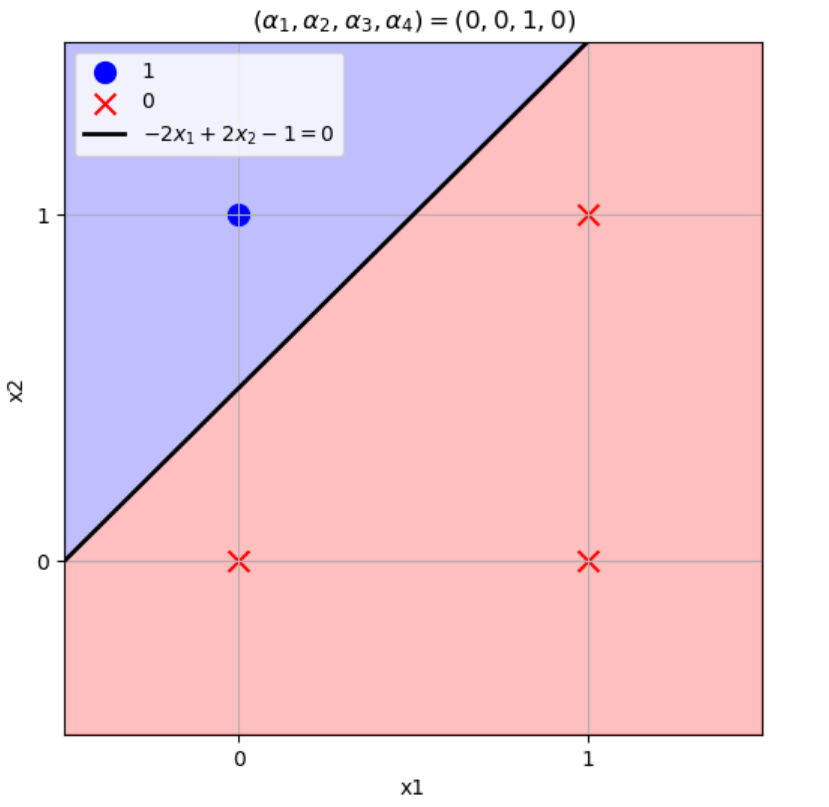
\((w_1,w_2)=(-2,2),b=-1\)のとき
\((x_1,x_2)=(0,0) \to w_1x_1+w_2x_2+b=-2\times0+2\times0-1=-1\leq0\)
\((x_1,x_2)=(1,0) \to w_1x_1+w_2x_2+b=-2\times1+2\times0-1=-3\leq0\)
\((x_1,x_2)=(0,1) \to w_1x_1+w_2x_2+b=-2\times0+2\times1-1=1>0\)
\((x_1,x_2)=(1,1) \to w_1x_1+w_2x_2+b=-2\times1+2\times1-1=-1\leq0\)
となりこの論理演算を表現できる。
\((\alpha_1,\alpha_2,\alpha_3,\alpha_4)=(0,0,0,1)\)はANDなので省略。
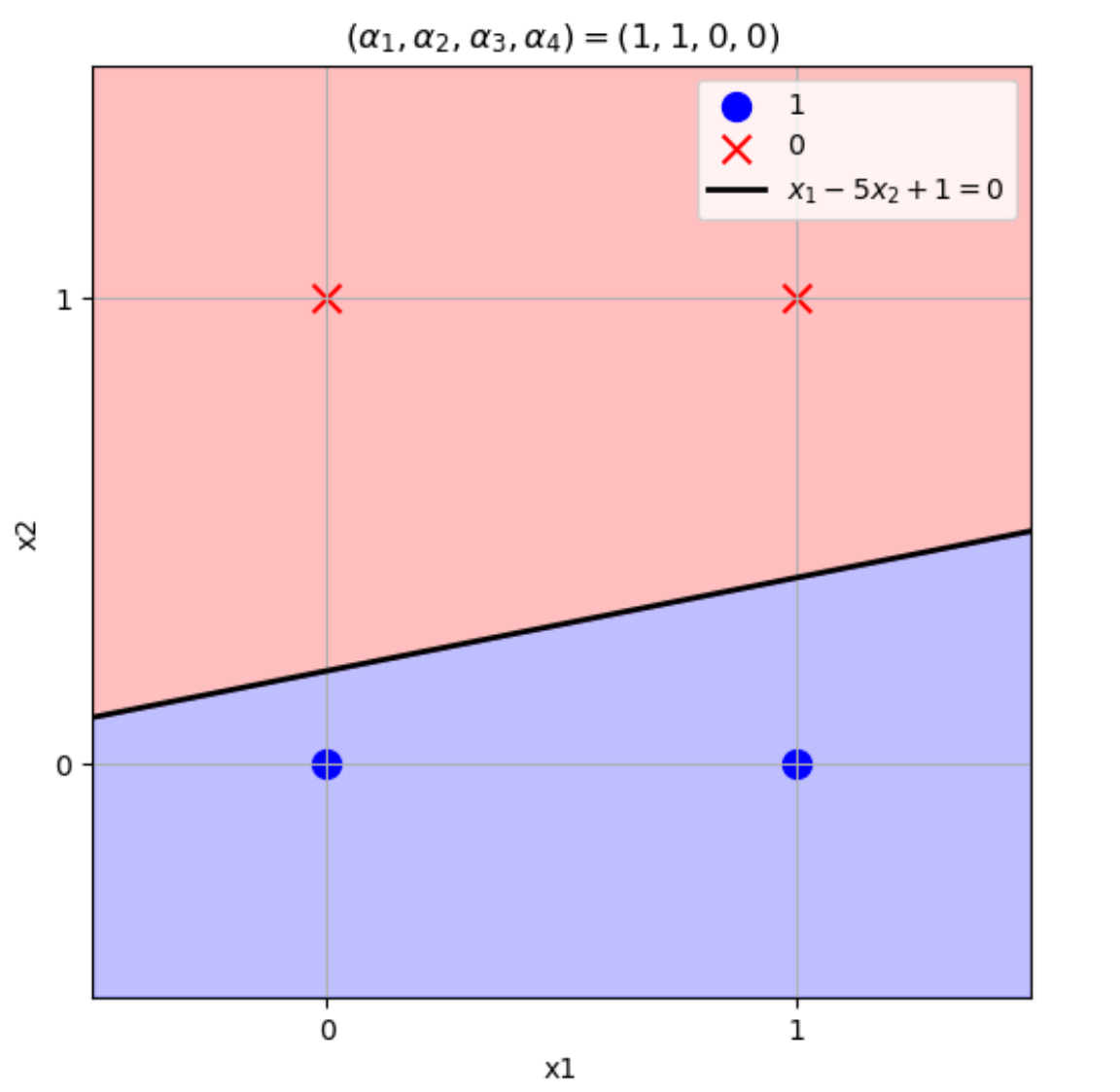
\((w_1,w_2)=(1,-5),b=1\)のとき
\((x_1,x_2)=(0,0) \to w_1x_1+w_2x_2+b=1\times0-5\times0+1=1>0\)
\((x_1,x_2)=(1,0) \to w_1x_1+w_2x_2+b=1\times1-5\times0+1=2>0\)
\((x_1,x_2)=(0,1) \to w_1x_1+w_2x_2+b=1\times0-5\times1+1=-4\leq0\)
\((x_1,x_2)=(1,1) \to w_1x_1+w_2x_2+b=1\times1-5\times1+1=-3\leq0\)
となりこの論理演算を表現できる。
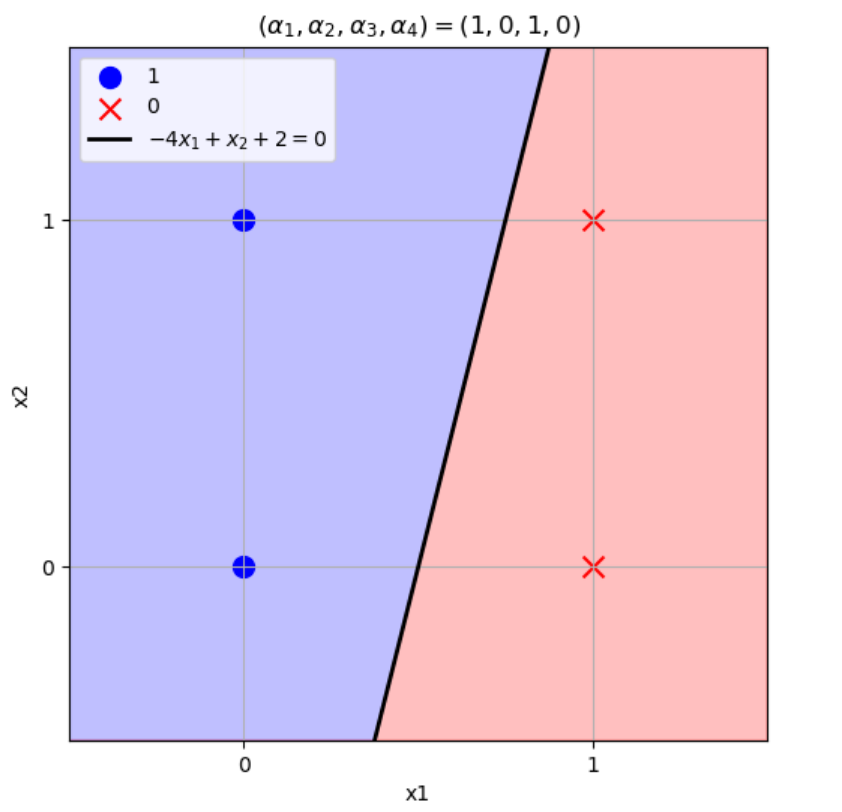
\((w_1,w_2)=(-4,1),b=2\)のとき
\((x_1,x_2)=(0,0) \to w_1x_1+w_2x_2+b=-4\times0+1\times0+2=2>0\)
\((x_1,x_2)=(1,0) \to w_1x_1+w_2x_2+b=-4\times1+1\times0+2=-2\leq0\)
\((x_1,x_2)=(0,1) \to w_1x_1+w_2x_2+b=-4\times0+1\times1+2=3>0\)
\((x_1,x_2)=(1,1) \to w_1x_1+w_2x_2+b=-4\times1+1\times1+2=-1\leq0\)
となりこの論理演算を表現できる。
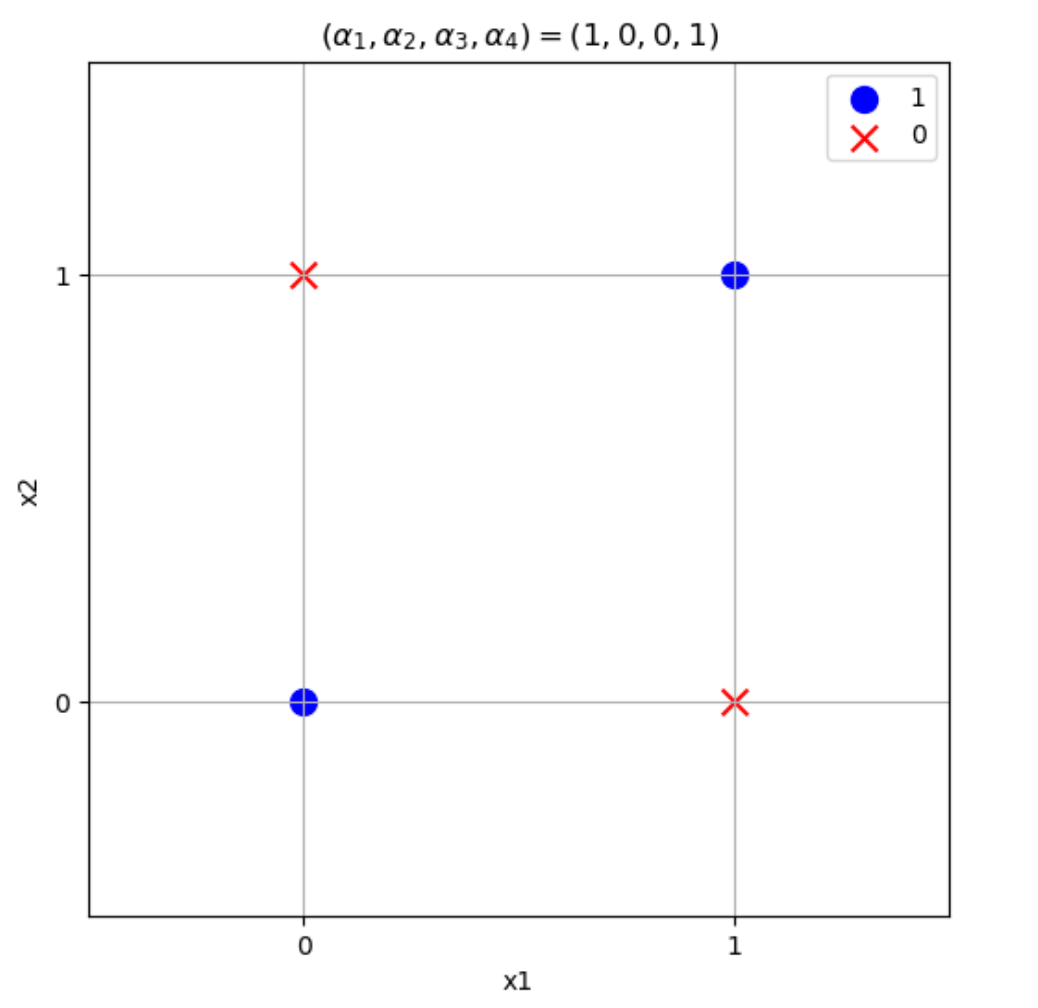
\((\alpha_1,\alpha_2,\alpha_3,\alpha_4)=(1,0,0,1)\)の論理演算はパーセプトロンで表現することができません。理由はXORのときと同じで、直線で分離することができないためです。
\((\alpha_1,\alpha_2,\alpha_3,\alpha_4)=(0,1,1,0)\)はXORなので省略。
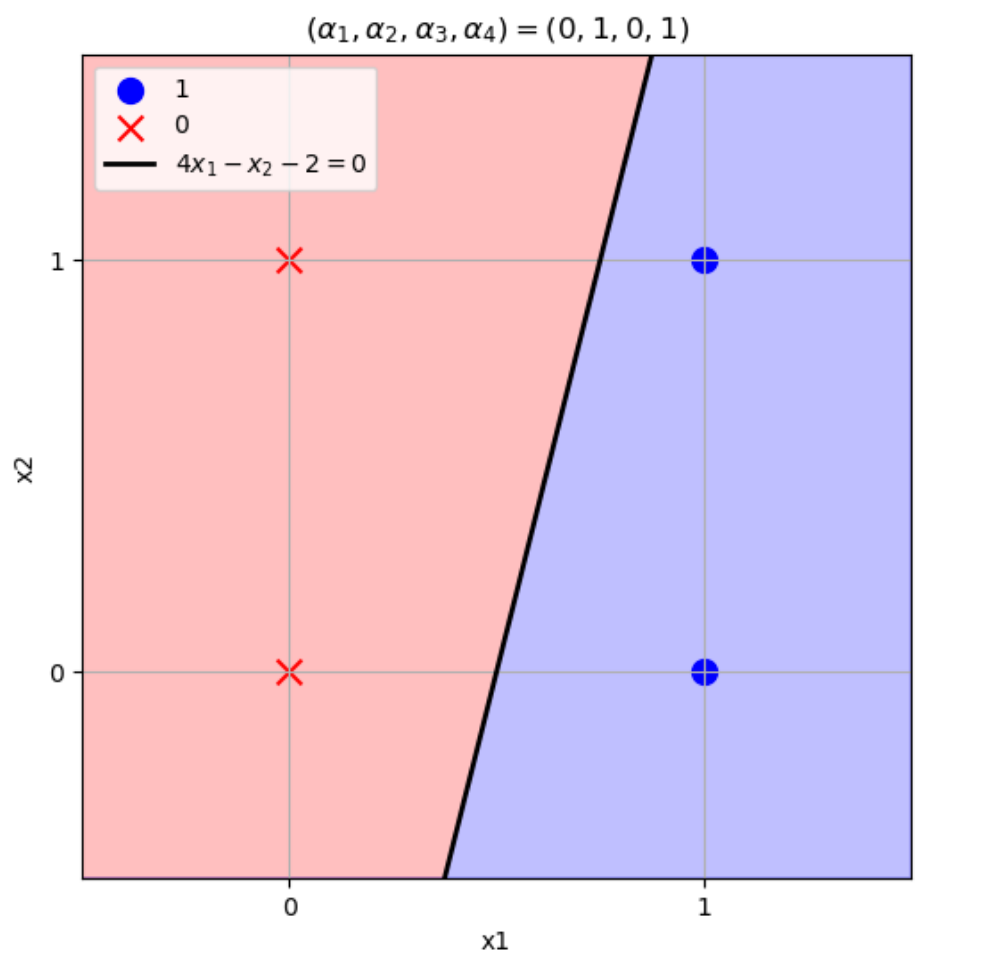
\((w_1,w_2)=(4,-1),b=-2\)のとき
\((x_1,x_2)=(0,0) \to w_1x_1+w_2x_2+b=4\times0-1\times0-2=-2\leq0\)
\((x_1,x_2)=(1,0) \to w_1x_1+w_2x_2+b=4\times1-1\times0-2=2>0\)
\((x_1,x_2)=(0,1) \to w_1x_1+w_2x_2+b=4\times0-1\times1-2=-3\leq0\)
\((x_1,x_2)=(1,1) \to w_1x_1+w_2x_2+b=4\times1-1\times1-2=1>0\)
となりこの論理演算を表現できる。
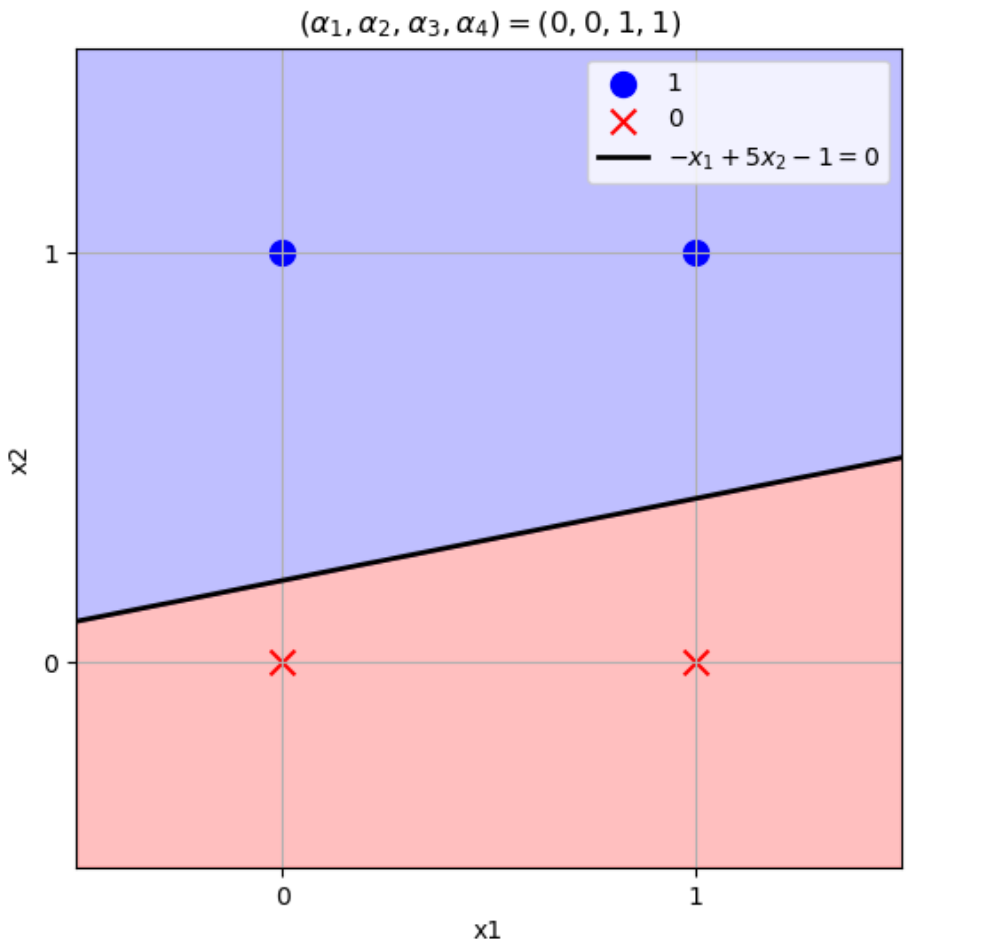
\((w_1,w_2)=(-1,5),b=-1\)のとき
\((x_1,x_2)=(0,0) \to w_1x_1+w_2x_2+b=-1\times0+5\times0-1=-1\leq0\)
\((x_1,x_2)=(1,0) \to w_1x_1+w_2x_2+b=-1\times1+5\times0-1=-2\leq0\)
\((x_1,x_2)=(0,1) \to w_1x_1+w_2x_2+b=-1\times0+5\times1-1=4>0\)
\((x_1,x_2)=(1,1) \to w_1x_1+w_2x_2+b=-1\times1+5\times1-1=3>0\)
となりこの論理演算を表現できる。
\((\alpha_1,\alpha_2,\alpha_3,\alpha_4)=(0,1,1,1)\)はORなので省略。
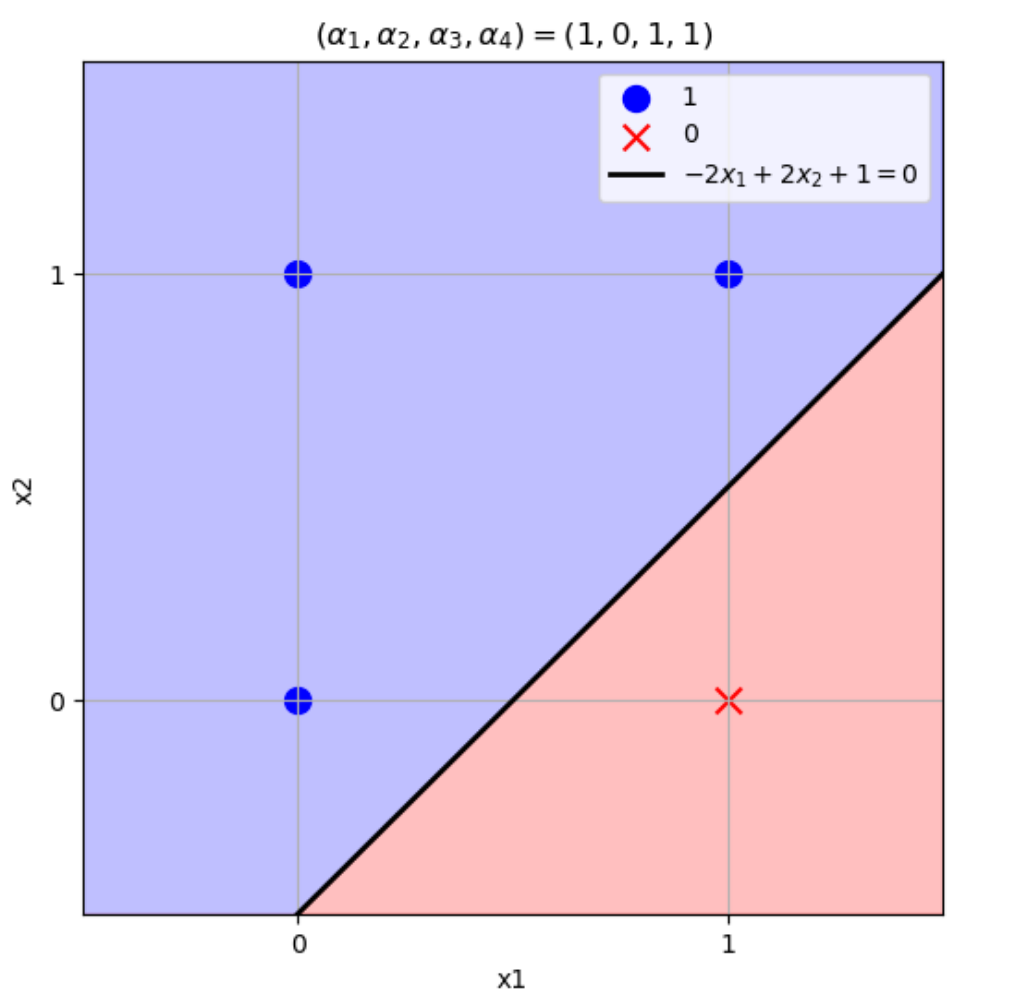
\((w_1,w_2)=(-2,2),b=1\)のとき
\((x_1,x_2)=(0,0) \to w_1x_1+w_2x_2+b=-2\times0+2\times0+1=1>0\)
\((x_1,x_2)=(1,0) \to w_1x_1+w_2x_2+b=-2\times1+2\times0+1=-1\leq0\)
\((x_1,x_2)=(0,1) \to w_1x_1+w_2x_2+b=-2\times0+2\times1+1=3>0\)
\((x_1,x_2)=(1,1) \to w_1x_1+w_2x_2+b=-2\times1+2\times1+1=1>0\)
となりこの論理演算を表現できる。
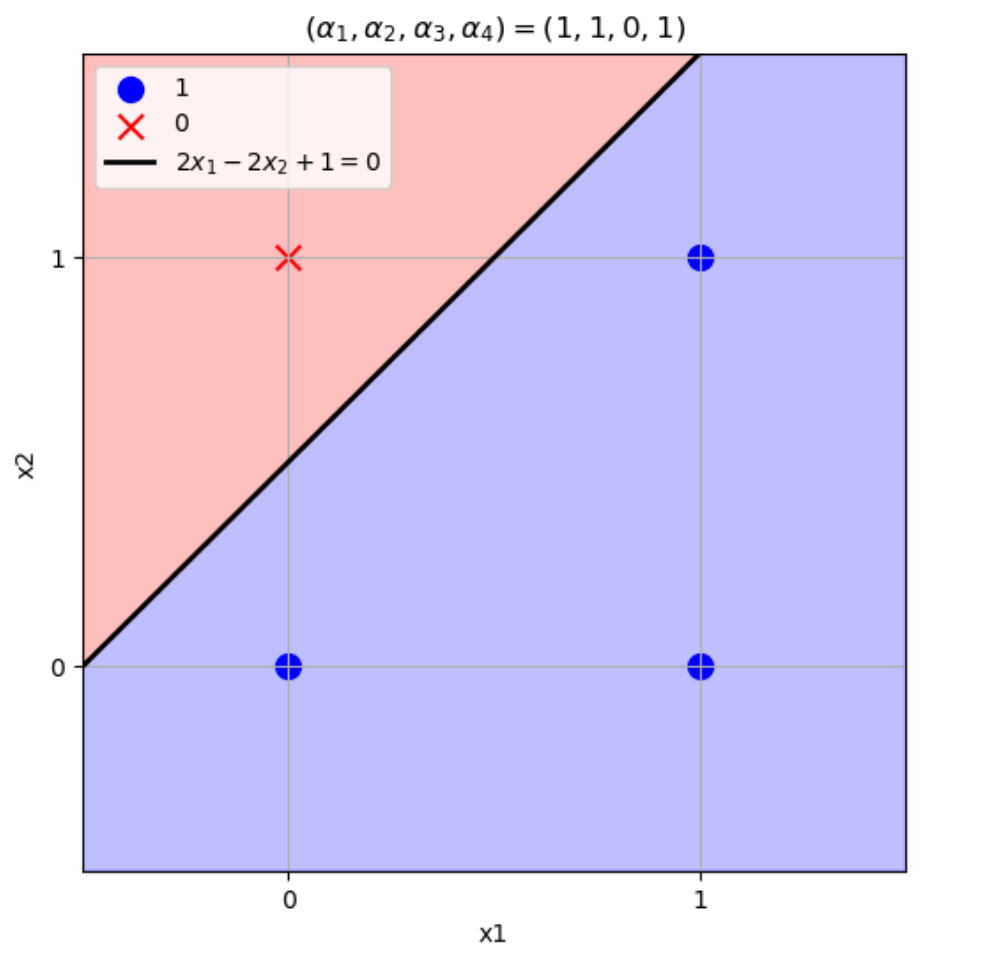
\((w_1,w_2)=(2,-2),b=1\)のとき
\((x_1,x_2)=(0,0) \to w_1x_1+w_2x_2+b=2\times0-2\times0+1=1>0\)
\((x_1,x_2)=(1,0) \to w_1x_1+w_2x_2+b=2\times1-2\times0+1=3>0\)
\((x_1,x_2)=(0,1) \to w_1x_1+w_2x_2+b=2\times0-2\times1+1=-1\leq0\)
\((x_1,x_2)=(1,1) \to w_1x_1+w_2x_2+b=2\times1-2\times1+1=1>0\)
となりこの論理演算を表現できる。
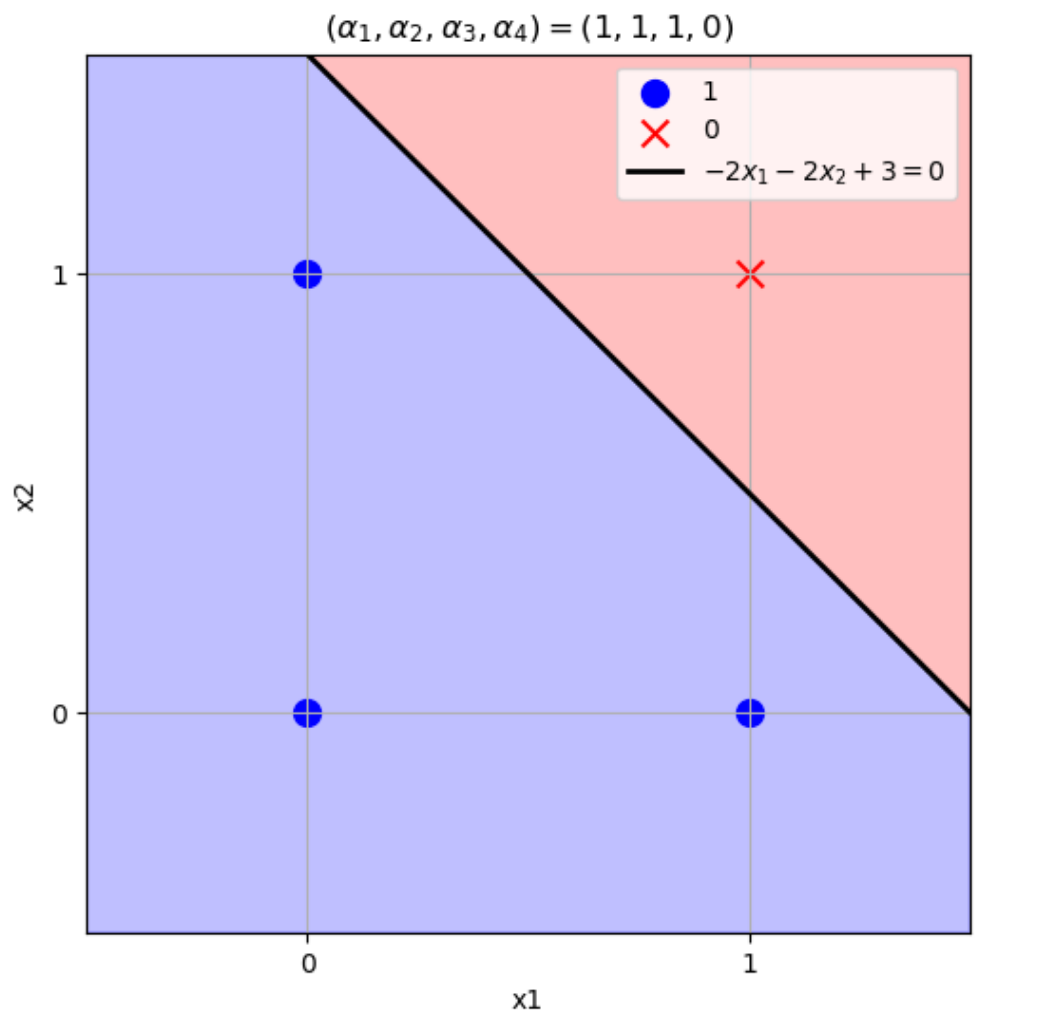
\((w_1,w_2)=(-2,-2),b=3\)のとき
\((x_1,x_2)=(0,0) \to w_1x_1+w_2x_2+b=-2\times0-2\times0+3=3>0\)
\((x_1,x_2)=(1,0) \to w_1x_1+w_2x_2+b=-2\times1-2\times0+3=1>0\)
\((x_1,x_2)=(0,1) \to w_1x_1+w_2x_2+b=-2\times0-2\times1+3=1>0\)
\((x_1,x_2)=(1,1) \to w_1x_1+w_2x_2+b=-2\times1-2\times1+3=-1\leq0\)
となりこの論理演算を表現できる。
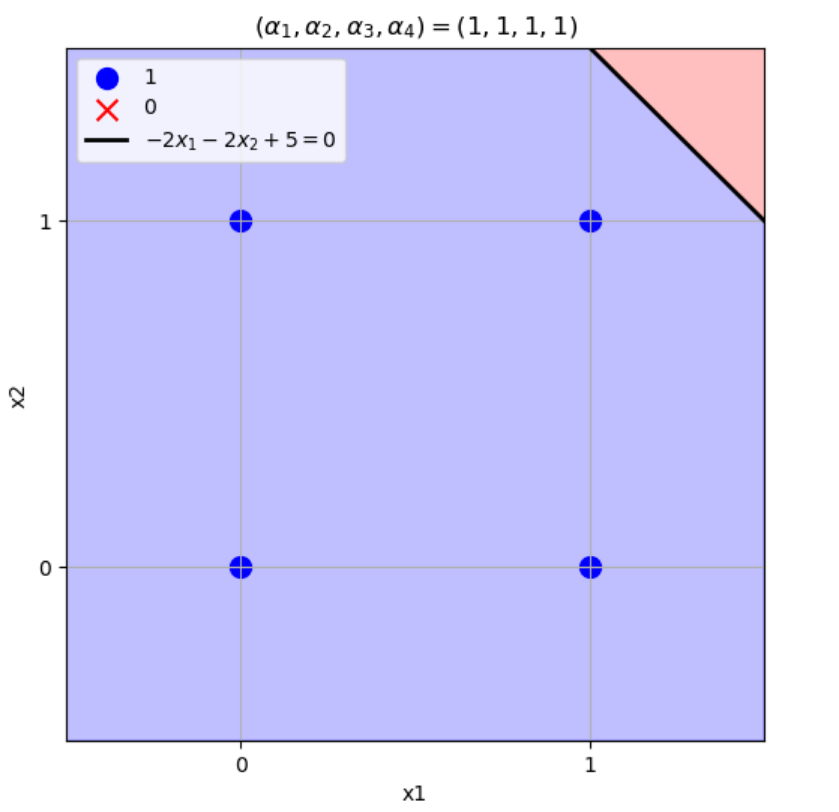
\((w_1,w_2)=(-2,-2),b=5\)のとき
\((x_1,x_2)=(0,0) \to w_1x_1+w_2x_2+b=-2\times0-2\times0+5=5>0\)
\((x_1,x_2)=(1,0) \to w_1x_1+w_2x_2+b=-2\times1-2\times0+5=3>0\)
\((x_1,x_2)=(0,1) \to w_1x_1+w_2x_2+b=-2\times0-2\times1+5=3>0\)
\((x_1,x_2)=(1,1) \to w_1x_1+w_2x_2+b=-2\times1-2\times1+5=1>0\)
となりこの論理演算を表現できる。
上の結果から\((\alpha_1,\alpha_2,\alpha_3,\alpha_4)=(0,1,1,0)\)と\((\alpha_1,\alpha_2,\alpha_3,\alpha_4)=(1,0,0,1)\)以外はパーセプトロンで表現できることが分かりました。
pythonで実装してみた
ここまでは論理演算をパーセプトロンで表現する方法について話してきましたが、最後にこれらをpythonで実装してみます。ここでは代表してANDとORを実装する方法を解説したいと思います。
ANDをpythonで実装する
# ANDを関数として定義
def AND(x1,x2):
(w1,w2,b) = (5,5,-7)
if w1*x1 + w2*x2 + b > 0:
return 1
else:
return 0
# AND関数にx1とx2を入力して結果を確認する
print(f"(x1,x2)=(0,0)のとき:{AND(0,0)}")
print(f"(x1,x2)=(1,0)のとき:{AND(1,0)}")
print(f"(x1,x2)=(0,1)のとき:{AND(0,1)}")
print(f"(x1,x2)=(1,1)のとき:{AND(1,1)}")
このコードを実行すると上のような結果が得られました。1つずつコードの解説をしていきます。
2行目ではANDを関数として定義しています。関数の名前は「AND」、引数は「x1」と「x2」です。
3行目では重みとバイアスを定義しています。第4章でANDを表現するためには\((w_1,w_2)=(5,5),b=-7\)とすれば良いことが分かったので「(w1,x1,b) = (5,5,-7)」としています。
4~5行目では、もし\(w_1x_1+w_2x_2+b>0\)だったら1を返すようにしています。
6~7行目では、もし\(w_1x_1+w_2x_2+b\leq0\)だったら0を返すようにしています。
9行目以降では今定義した「AND」関数に実際に数値を入力したときの返り値を表示するようにしています。
結果を見るとちゃんと「(x1,x2)=(1,1)」のときだけ1が返されて、それ以外の入力では0が返されていますね。
ORをpythonで実装する
# ORを関数として定義
def OR(x1,x2):
(w1,w2,b) = (5,5,-2)
if w1*x1 + w2*x2 + b > 0:
return 1
else:
return 0
# OR関数にx1とx2を入力して結果を確認する
print(f"(x1,x2)=(0,0)のとき:{OR(0,0)}")
print(f"(x1,x2)=(1,0)のとき:{OR(1,0)}")
print(f"(x1,x2)=(0,1)のとき:{OR(0,1)}")
print(f"(x1,x2)=(1,1)のとき:{OR(1,1)}")
このコードを実行すると上のような結果が得られました。1つずつコードの解説をしていきます。
2行目ではORを関数として定義しています。関数の名前は「OR」、引数は「x1」と「x2」です。
3行目では重みとバイアスを定義しています。第4章でANDを表現するためには\((w_1,w_2)=(5,5),b=-2\)とすれば良いことが分かったので「(w1,x1,b) = (5,5,-2)」としています。
4~5行目では、もし\(w_1x_1+w_2x_2+b>0\)だったら1を返すようにしています。
6~7行目では、もし\(w_1x_1+w_2x_2+b\leq0\)だったら0を返すようにしています。
9行目以降では今定義した「OR」関数に実際に数値を入力したときの返り値を表示するようにしています。
結果を見るとちゃんと「(x1,x2)=(0,0)」のときだけ0が返されて、それ以外の入力では1が返されていますね。
おわりに
いかがでしたか。
今回の記事ではパーセプトロンと論理演算について解説しました。
今後もこのようなAI・機械学習に関する記事を書いていきます!
最後までこの記事を読んでくれてありがとうございました。
参考文献





