- 最適化結果がinfeasibleになったときどうすれば良いの?
- 矛盾する制約を見つけたい…
- scipでIISを計算する方法は?
こんにちは、しゅんです!
実務で最適化問題を解いていると、「許容解なし(Infeasible)」という結果に頭を抱えるのはあるあるですよね。特に巨大なモデルになるほど、どの制約同士が矛盾しているのかを自力で見つけるのは至難の業です。
そんな悩みを解決してくれる待望の機能が最近のSCIPのアップデートで追加されました!なんと許容解がないときに矛盾の原因となっている制約(IIS)を自動で計算してくれるようになったのです。
ということで今回の記事では、PySCIPOptを使ってこの新機能を動かす方法を分かりやすく解説します!
それではやっていきましょう!
【Udemy講座公開のお知らせ】
このたびUdemyで数理最適化の講座を公開しました!この講座は「数理最適化を勉強してみたいけど数式が多くて難しい…」という方向けに、どうやって最適化問題を定式化すれば良いかを優しく丁寧に解説しています!
実務で最適化問題を解くときに許容解が無いことはよくある
実務で最適化問題を解いていると、クライアントからの細かな要望をすべて制約条件として盛り込んだ結果、いざ実行してみると許容解なし(Infeasible)という結果が得られてしまうのはよくある話です。
モデルの規模が小さければ、どの制約が矛盾しているのかを見つけるのは割と簡単です。しかし大規模なモデルになると矛盾する制約を見つけるのは簡単じゃなく、それを見つけるのにめっちゃ時間がかかったりします。
そんな時に、どの制約が矛盾しているのかを見つける方法の1つが、ソルバーに搭載されているIIS(Irreducible Inconsistent Subsystem)を計算する機能を利用することです。
IISってなに?
IISを簡単に言うと、「そのままだと矛盾している制約のグループの中から、これ以上削れないところまで絞り込んだ最小単位の集合」のことです。
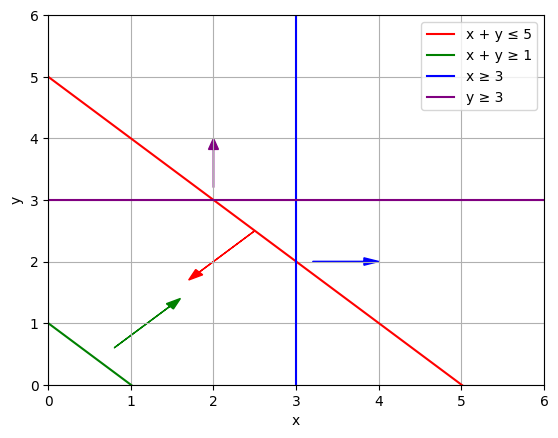
例えば以下の4つの制約を考えます。ただし\(x,y\)は変数とします。
\(x+y \leq 5,\)
\(x+y \geq 1,\)
\(x \geq 3,\)
\(y \geq 3.\)
上の4つの制約をすべて満たす \(x,y\) の組は存在しないので、この制約を持つ最適化問題を解くとinfeasibleとなります。じゃあなんでinfeasibleになるのかを考えると、\(x+y \leq 5\)と\(x\geq 3\)と\(y \geq 3\)が矛盾しているからですね。逆に\(x+y \geq 1\)はあってもなくてもinfeasibleなことは変わらないですね。従ってIISは\(x+y \leq 5\)と\(x\geq 3\)と\(y \geq 3\)の3つの制約となります。
IISを計算する機能はGUROBIやCPLEXには既に搭載されていましたがこれまでSCIPにはなかったです。しかし2025年11月のアップデートで、ついにSCIPにもIISを計算する機能が追加されました!ということでここからは実際にPySCIPOptでIISを計算する機能を使用してみたいと思います。
IISは日本語で既約不整合部分系と呼ばれます。
PySCIPOptでIISを計算してみた
それではここからは実際にPySCIPOptでIISを計算してみたいと思います!
IISが計算できるバージョンはv10.0.0以降
それではまずscipをダウンロードします。2026年1月14日時点での最新バージョンであるv10.0.0をダウンロードします。
PySCIPOptでIISが計算できるのはv10.0.0以降であることに注意してください。
ローカルにダウンロードしても良いですし、dockerで環境構築しても良いです。ローカルにダウンロードしてSCIPを使う手順は過去の記事で解説しているのでそちらを参考にしてください。
\\ 過去の記事はこちらから! //
問題例1(簡単な線形計画問題)
それではまず最初に第3章で紹介した、4つの制約を持つ最適化問題を解いてみます。サンプルコードは下記の通りです。
from pyscipopt import Model
def main():
# モデルの作成
model = Model("Sample Problem")
# 変数の作成
x = model.addVar("x", vtype="C")
y = model.addVar("y", vtype="C")
# 矛盾する制約の追加(cos1, cons3, cons4が矛盾)
c1 = model.addCons(x + y <= 5, name="cons1")
c2 = model.addCons(x + y >= 1, name="cons2")
c3 = model.addCons(x >= 3, name="cons3")
c4 = model.addCons(y >= 3, name="cons4")
# 目的関数の追加
model.setObjective(x, "maximize")
model.hideOutput() # ログを非表示
model.optimize() # 最適化の実行
status = model.getStatus()
print(f"最適化ステータス: {status}")
iis = model.generateIIS()
sub_model = iis.getSubscip()
print(f"矛盾する制約: {sub_model.getConss()}")
if __name__ == "__main__":
main()
コードの説明
簡単にコードの説明をします。
# モデルの作成
model = Model("Sample Problem")まずこの部分で最適化モデルのクラスを「model」と定義しています。適当にモデルの名前は”Sample Problem”としました。
# 変数の作成
x = model.addVar("x", vtype="C")
y = model.addVar("y", vtype="C")この部分で変数の作成をしています。変数は「.addVar」で追加することができます。\(x,y\)どちらも連続変数(vtype=”C”)として定義します。
# 矛盾する制約の追加(cos1, cons3, cons4が矛盾)
c1 = model.addCons(x + y <= 5, name="cons1")
c2 = model.addCons(x + y >= 1, name="cons2")
c3 = model.addCons(x >= 3, name="cons3")
c4 = model.addCons(y >= 3, name="cons4")次にこの部分で制約を追加しています。制約は「.addCons」で追加することができます。第3章で説明したようにcons1, cons3, cons4が矛盾しています。
# 目的関数の追加
model.setObjective(x, "maximize")次にこの部分で目的関数を追加しています。別に目的関数は何でもよいので、適当に\(x\)の最大化にしました。
model.hideOutput() # ログを非表示
model.optimize() # 最適化の実行
status = model.getStatus()
print(f"最適化ステータス: {status}")この部分で最適化の実行→最適化結果の取得→最適化結果の表示をしています。「.hideOutput」で最適化実行ログを火表示しています。別に表示しても良いです。
「.optimize」で最適化の実行をしています。「.getStatus」で解の状態を取得します。今回は”infeasible”が返ってくるはずです。そしてそれをprint文で表示するようにしています。
iis = model.generateIIS()
sub_model = iis.getSubscip()
print(f"矛盾する制約: {sub_model.getConss()}")ここが本題のIISを計算して結果を表示する部分です。「.generateIIS」でIISを計算します。「.getSubscip」で矛盾する最小限の制約持つサブ最適化モデルを取得します。最後にサブモデルに含まれる制約を「.getConss」で取得して、printしています。サブモデルに含まれる制約は矛盾する最小限の制約となっています。
IISの計算結果を見る
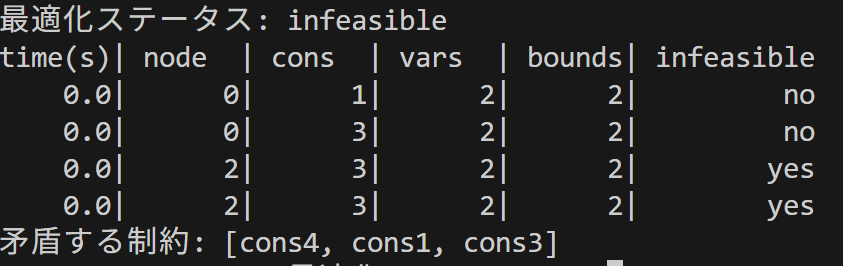
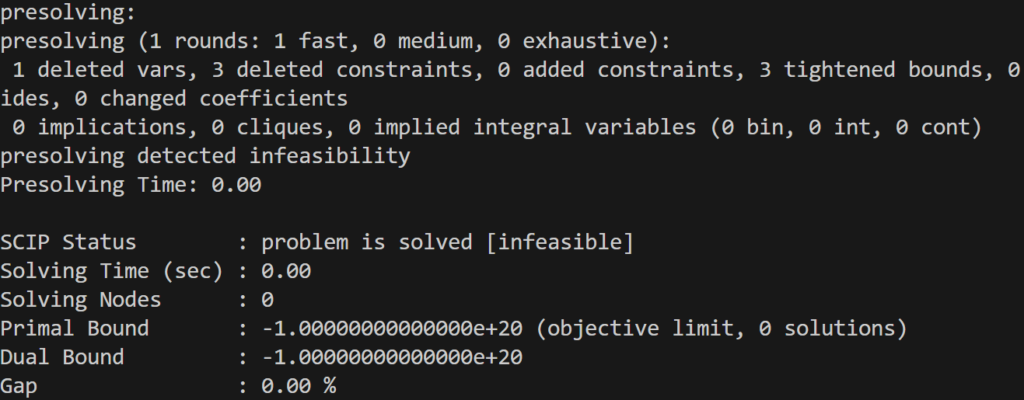
それではIISの計算結果を見てみましょう。まず1行目は最適化結果を表示しています。ちゃんとinfeasibleになっていますね。つづいてIISの計算過程がまとめられた表が出力されています。
表のcons、varsがそれぞれサブモデルに含まれる変数、制約の数を表しており、boundsが変数の上下限制約の数を表しています。infeasibleの列はそのサブモデルがinfeasibleかどうかを表していて、noだと実行可能(feasible)、yesだと実行不能(infeasible)を表しています。上の表の一番下の行が制約数が3、変数の数が2となっており、これがIISとして出力されています。
最後に矛盾する制約としてちゃんと「cons4, cons1, cons3」が出力されていますね。この3つの制約のどれか1つを取り除けば実行可能になることが分かりました。
問題例2(配送計画問題)
問題例1はちょっと簡単すぎるのでもう少し現実的な問題として、容量制約付き配送計画問題を例にしてIISを計算してみたいと思います。定式化の方法は省略しますが、過去の記事で解説しているので詳しく知りたい方はぜひそちらも見てみてください。
\\\ 配送計画問題の定式化方法を紹介している記事はこちらから! ///
サンプルコードは下記の通りです。
from pyscipopt import Model, quicksum
import itertools
def main():
## データ設定
m = 3 # 車両数
n = 8 # 地点数
V = [i for i in range(n + 1)] # デポを含む地点の集合
V_0 = V[1:] # デポを含まない地点の集合
R = [r for r in range(m)] # 車両の集合
# 各地点の需要
q = {
1: 5,
2: 7,
3: 9,
4: 11,
5: 11,
6: 14,
7: 15,
8: 16,
}
Q = 20 # 車両の容量
# 距離(全て1とする)
d = {}
for i in V:
for j in V:
d[(i,j)] = 1
## 最適化問題の定式化
# モデルの定義
model = Model("CVRP")
# 変数定義
x = {}
for r in R:
for i in V:
for j in V:
if i != j:
x[(r, i, j)] = model.addVar(f"x_{r}_{i}_{j}", vtype="B")
# 目的関数 (距離最小化)
model.setObjective(
quicksum(d[(i,j)] * x[(r, i, j)] for r in R for i in V for j in V if i != j),
"minimize"
)
# 制約条件1 各地点にはちょうど1回だけ訪れる
for j in V_0:
model.addCons(
quicksum(x[(r, i, j)] for r in R for i in V if i != j) == 1,
name=f"VisitOnce_{j}"
)
# 制約条件2 車両は必ずデポから出発する
for r in R:
model.addCons(
quicksum(x[(r, 0, j)] for j in V_0) == 1,
name=f"DepartDepot_{r}"
)
# 制約条件3 フロー保存則 (入った回数 = 出る回数)
for j in V:
for r in R:
model.addCons(
quicksum(x[(r, i, j)] for i in V if i != j) -
quicksum(x[(r, j, k)] for k in V if j != k) == 0,
name=f"FlowConst_{r}_{j}"
)
# 制約条件4 容量制約
for r in R:
model.addCons(
quicksum(q[j] * x[(r, i, j)] for i in V for j in V_0 if i != j) <= Q,
name=f"Capacity_{r}"
)
# 制約条件5 部分巡回路除去 (Subtour Elimination)
# V_0の全ての部分集合を作成
def powerset(iterable):
s = list(iterable)
return itertools.chain.from_iterable(itertools.combinations(s, r) for r in range(len(s)+1))
subsets = powerset(V_0)
for S in subsets:
if len(S) >= 2:
model.addCons(
quicksum(x[(r, i, j)] for r in R for i in S for j in S if i != j) <= len(S) - 1,
name=f"Subtour_{S}"
)
## 最適化の実行とIIS解析
model.hideOutput()
model.optimize()
status = model.getStatus()
print(f"最適化ステータス: {status}")
iis = model.generateIIS()
sub_model = iis.getSubscip()
print("--- 矛盾する制約 ---")
for c in sub_model.getConss():
print(f"- {c.name}")
if __name__ == "__main__":
main()
コードの説明
こちらも簡単にコードの説明をします。
## データ設定
m = 3 # 車両数
n = 8 # 地点数
V = [i for i in range(n + 1)] # デポを含む地点の集合
V_0 = V[1:] # デポを含まない地点の集合
R = [r for r in range(m)] # 車両の集合
# 各地点の需要
q = {
1: 5,
2: 7,
3: 9,
4: 11,
5: 11,
6: 14,
7: 15,
8: 16,
}
Q = 20 # 車両の容量
# 距離(全て1とする)
d = {}
for i in V:
for j in V:
d[(i,j)] = 1まずこの部分では各種パラメータを定義しています。infeasibleな問題例を作るため、車両数と容量に対して各地点の需要をちょっと多めに設定しています。
なお距離は全て1としていますが、今回はinfeasibleな問題を解くことが目的なので何でもよいです。
# モデルの定義
model = Model("CVRP")この部分でモデルの定義をしています。名前はCVRPとしています。
# 変数定義
x = {}
for r in R:
for i in V:
for j in V:
if i != j:
x[(r, i, j)] = model.addVar(f"x_{r}_{i}_{j}", vtype="B")この部分で変数の定義をしています。
# 目的関数 (距離最小化)
model.setObjective(
quicksum(d[(i,j)] * x[(r, i, j)] for r in R for i in V for j in V if i != j),
"minimize"
)この部分で目的関数を定義しています。目的関数は移動距離の最小化とします。
# 制約条件1 各地点にはちょうど1回だけ訪れる
for j in V_0:
model.addCons(
quicksum(x[(r, i, j)] for r in R for i in V if i != j) == 1,
name=f"VisitOnce_{j}"
)
# 制約条件2 車両は必ずデポから出発する
for r in R:
model.addCons(
quicksum(x[(r, 0, j)] for j in V_0) == 1,
name=f"DepartDepot_{r}"
)
# 制約条件3 フロー保存則 (入った回数 = 出る回数)
for j in V:
for r in R:
model.addCons(
quicksum(x[(r, i, j)] for i in V if i != j) -
quicksum(x[(r, j, k)] for k in V if j != k) == 0,
name=f"FlowConst_{r}_{j}"
)
# 制約条件4 容量制約
for r in R:
model.addCons(
quicksum(q[j] * x[(r, i, j)] for i in V for j in V_0 if i != j) <= Q,
name=f"Capacity_{r}"
)
# 制約条件5 部分巡回路除去 (Subtour Elimination)
# V_0の全ての部分集合を作成
def powerset(iterable):
s = list(iterable)
return itertools.chain.from_iterable(itertools.combinations(s, r) for r in range(len(s)+1))
subsets = powerset(V_0)
for S in subsets:
if len(S) >= 2:
model.addCons(
quicksum(x[(r, i, j)] for r in R for i in S for j in S if i != j) <= len(S) - 1,
name=f"Subtour_{S}"
)
この部分で制約条件を定義しています。
## 最適化の実行とIIS解析
model.hideOutput()
model.optimize()
status = model.getStatus()
print(f"最適化ステータス: {status}")
iis = model.generateIIS()
sub_model = iis.getSubscip()
print("--- 矛盾する制約 ---")
for c in sub_model.getConss():
print(f"- {c.name}")
この部分で「最適化の実行→最適化結果の表示→IISの計算→矛盾する制約の表示」を行っています。
IISの計算結果を見る
最適化ステータス: infeasible
time(s)| node | cons | vars | bounds| infeasible
0.0| 0| 9| 216| 432| no
0.0| 0| 277| 216| 432| no
1.0| 1| 279| 216| 432| yes
1.0| 2| 261| 216| 432| yes
2.0| 4| 252| 216| 432| yes
3.0| 5| 234| 216| 432| yes
4.0| 8| 225| 216| 432| yes
5.0| 10| 216| 216| 432| yes
6.0| 12| 207| 216| 432| yes
6.0| 13| 189| 216| 432| yes
7.0| 16| 180| 216| 432| yes
7.0| 19| 171| 216| 432| yes
8.0| 22| 162| 216| 432| yes
8.0| 23| 144| 216| 432| yes
9.0| 25| 135| 216| 432| yes
time(s)| node | cons | vars | bounds| infeasible
9.0| 27| 126| 216| 432| yes
9.0| 28| 108| 216| 432| yes
10.0| 30| 99| 216| 432| yes
10.0| 32| 90| 216| 432| yes
11.0| 35| 81| 216| 432| yes
11.0| 36| 63| 216| 432| yes
11.0| 38| 62| 216| 432| yes
11.0| 39| 60| 216| 432| yes
11.0| 41| 59| 216| 432| yes
11.0| 43| 58| 216| 432| yes
11.0| 45| 57| 216| 432| yes
11.0| 47| 56| 216| 432| yes
11.0| 49| 55| 216| 432| yes
12.0| 50| 53| 216| 432| yes
12.0| 51| 49| 216| 432| yes
time(s)| node | cons | vars | bounds| infeasible
12.0| 53| 48| 216| 432| yes
12.0| 54| 46| 216| 432| yes
12.0| 56| 45| 216| 432| yes
12.0| 58| 44| 216| 432| yes
12.0| 59| 42| 216| 432| yes
12.0| 60| 38| 216| 432| yes
12.0| 61| 30| 216| 432| yes
12.0| 63| 29| 216| 432| yes
12.0| 64| 27| 216| 432| yes
12.0| 65| 26| 216| 432| yes
13.0| 66| 25| 216| 432| yes
13.0| 70| 24| 216| 432| yes
13.0| 71| 22| 216| 432| yes
13.0| 72| 18| 216| 432| yes
13.0| 73| 10| 216| 432| yes
time(s)| node | cons | vars | bounds| infeasible
13.0| 74| 7| 216| 432| yes
13.0| 74| 7| 192| 384| yes
--- 矛盾する制約 ---
- VisitOnce_7
- VisitOnce_6
- VisitOnce_5
- Capacity_1
- Capacity_0
- Capacity_2
- VisitOnce_4長かったのでスクショじゃなくてログを貼っています。まず最適化ステータスはinfeasibleになっていますね。そして2行目以降がIISの計算過程を表しています。問題例1と違ってかなり長い間計算していることが分かります。
最初は279本の制約で初めてinfeasibleとなり、そこから少しずつ制約の数を減らしていった結果7本まで制約を減らすことができています。
そして最終的に残った7つの制約は
「頂点4,5,6,7にちょうど1回訪れ、車両0,1,2の容量制約を満たす」
ことを表しています。地点4,5,6,7の需要はそれぞれ11,11,14,15で、車両0,1,2の容量はいずれも20です。従ってどの車両も高々1つの地点しか訪れることができません。(一番需要が小さい地点4,5を回ろうとしても22の容量が必要です)
従ってこの時点でinfeasibleとなってしまうのです。ということでこの部分がボトルネックになっているということが分かりました。
おわりに
今回は最近のSCIPのアップデートで追加されたIISを計算する機能を紹介しました!
今後もこのような数理最適化に関する記事を書いていきます!
最後までこの記事を読んでくれてありがとうございました。
普段は組合せ最適化の記事を書いてたりします。
ぜひ他の記事も読んでみてください!
このブログの簡単な紹介はこちらに書いてあります。
興味があったら見てみてください。
このブログでは経営工学を勉強している現役理系大学生が、経営工学に関することを色々話していきます!
ぼくが経営工学を勉強している中で感じたことや、興味深かったことを皆さんと共有出来たら良いなと思っています。
そもそも経営工学とは何なのでしょうか。Wikipediaによると
経営工学(けいえいこうがく、英: engineering management)は、人・材料・装置・情報・エネルギーを総合したシステムの設計・改善・確立に関する活動である。そのシステムから得られる結果を明示し、予測し、評価するために、工学的な分析・設計の原理・方法とともに、数学、物理および社会科学の専門知識と経験を利用する。
引用元 : 経営工学 – Wikipedia
長々と書いてありますが、要は経営、経済の課題を理系的な観点から解決する学問です。





