こんにちは!しゅんです!
このブログでは経営工学を勉強している現役理系大学生が、経営工学に関することを色々話していきます!
ぼくが経営工学を勉強している中で感じたことや、興味深かったことを皆さんと共有出来たら良いなと思っています。
そもそも経営工学とは何なのでしょうか。Wikipediaによると
経営工学(けいえいこうがく、英: engineering management)は、人・材料・装置・情報・エネルギーを総合したシステムの設計・改善・確立に関する活動である。そのシステムから得られる結果を明示し、予測し、評価するために、工学的な分析・設計の原理・方法とともに、数学、物理および社会科学の専門知識と経験を利用する。
引用元 : 経営工学 – Wikipedia
長々と書いてありますが、要は経営、経済の課題を理系的な観点から解決する学問です。

今回の記事ではNBAのスタッツを使ってデータ分析をしてみたいと思います!
経営工学とは少し離れるかもしれませんが、データ分析に興味がある人、NBAに興味がある人はぜひ今回の記事を読んでみてください!!!
この記事は前回からの続きなのでこれまでの記事を見てから読むと分かりやすいです!
平均値を求めよう
それでは早速平均値を求めてみましょう。
全員の数値を全部足して人数で割った数

ということでgoogle colabでやってみましょう。
# 平均値を計算したい指標をまとめる(今回はFG%, 3P%, 2P%, FT%, PTSの平均を求める)
for i in ["FG%", "3P%", "2P%", "FT%", "PTS"]:
# 平均値を表示する(meanは平均値を表す)
print(i, df[i].mean())
ということで平均値が計算できました。
これらはNBAの選手全体の平均値になっています。(PTSは1試合当たりの得点数)
ポジションごとの平均値を求めよう
先ほど計算した平均値はNBAの全選手のものです。
しかしバスケにはポジションがあり、各ポジションで役割が異なります。そのためポジションごとで比較をする必要がありそうです。
ということで各ポジションの平均値を求めてみましょう。今回は3P%, 2P%, FT%の3つについて計算していきます。
#データをポジションごとに分ける
df_PG = df[df["Pos"] == "PG"]
df_SG = df[df["Pos"] == "SG"]
df_SF = df[df["Pos"] == "SF"]
df_PF = df[df["Pos"] == "PF"]
df_C = df[df["Pos"] == "C"]##各ポジションのシュート効率の平均を求める
#各ポジションごとのスタッツを格納するリストを作る
data1 = [] #PG用
data2 = [] #SG用
data3 = [] #SF用
data4 = [] #PF用
data5 = [] #C用
# ポジションごとに3P%, 2P%, FT%の3つのスタッツの平均値を求める
for i in ["3P%", "2P%", "FT%"]:
data1.append(df_PG[i].mean())
data2.append(df_SG[i].mean())
data3.append(df_SF[i].mean())
data4.append(df_PF[i].mean())
data5.append(df_C[i].mean())
# dataをまとめる
data_Pos =[data1, data2, data3, data4, data5]
# 得られたデータをデータフレーム形式にする
mean_Pos_df = pd.DataFrame(data = data_Pos, columns=["3P%", "2P%", "FT%"], index=pd.Index(["PG","SG", "SF", "PF", "C"], name = "ポジション"))
# データフレームの表示
mean_Pos_df 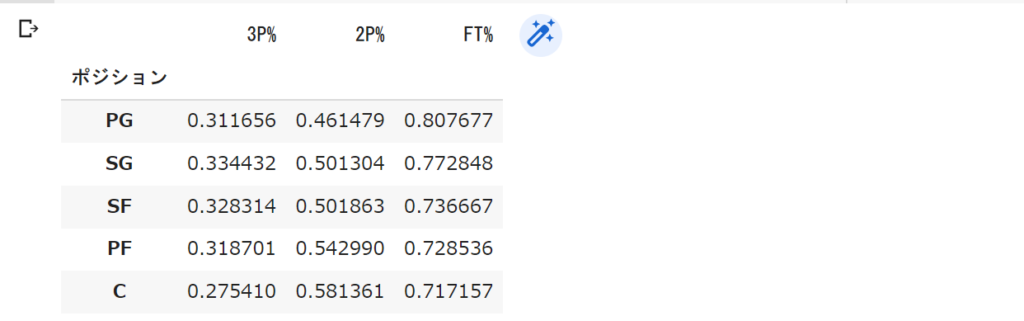
データフレーム形式で表示してみました。データフレームについて勉強したい人は「pandas データフレーム」とかで調べてみてください!
これを見るとシュート成功率に何かしら関係がありそうですね。
一般的にPG→Cにポジションが変わるにつれてインサイドでの攻撃回数が多くなるので、3P%は低くなり2P%は高くなります。(最近のNBAの選手ではCなのに3Pめっちゃ決める選手もいますね笑)
上の平均値の表を見ても同じような傾向が見られますね。
となるとPGの3P%が2番目に低いのが気になりますね。
本来ならPGの3P%は高くなるはずなのにこれは一体何が原因なのでしょうか、機会があれば分析したいですね。
(現時点のぼくの考えは単純に3Pの試投数が多いからだと思いますが分析してみないと分かりませんね笑)
上位選手の平均値を求めよう
ということで次は各ポジションに関してTOP30の平均値を求めていきます。今回は代表して3P%のTOP30を求めます。
# 各ポジションを3P%の高い順に並べる(ascending = Falseにすることで降順になる)
df_PG = df_PG.sort_values("3P%",ascending=False)
df_SG = df_SG.sort_values("3P%",ascending=False)
df_SF = df_SF.sort_values("3P%",ascending=False)
df_PF = df_PF.sort_values("3P%",ascending=False)
df_C = df_C.sort_values("3P%",ascending=False)
#各ポジションの3P%ランキングTOP30を抽出する
df_PG_30 = df_PG.head(30)
df_SG_30 = df_SG.head(30)
df_SF_30 = df_SF.head(30)
df_PF_30 = df_PF.head(30)
df_C_30 = df_C.head(30)# 各ポジションの平均値を格納するリストを作成
data = []
# すべてのポジションに対して平均値を求める
for i in [df_PG_30, df_SG_30, df_SF_30, df_PF_30, df_C_30]:
data.append(i["3P%"].mean())
# 得られたデータをデータフレーム形式にする
mean_Pos_df_30 = pd.DataFrame(data = data, columns=["3P%"], index=pd.Index(["PG","SG", "SF", "PF", "C"], name = "ポジション"))
# データフレームの表示
mean_Pos_df_30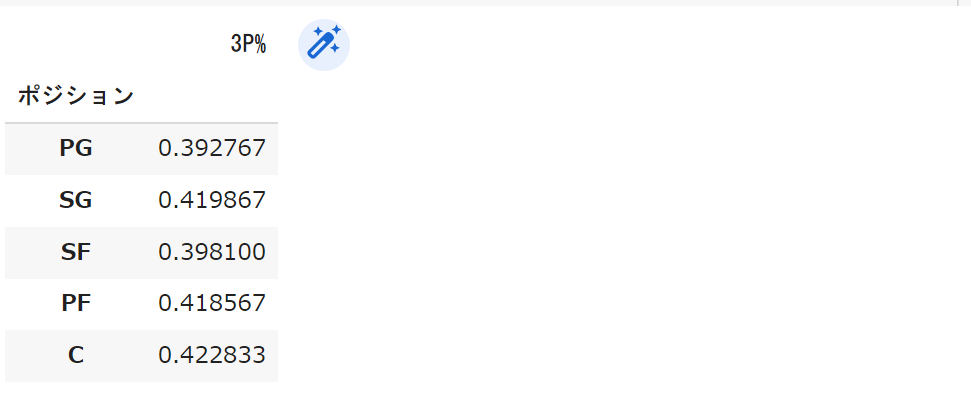
見てみるとどのポジションでもだいたい4割超えていますね。NBAでは50-40-90という功績があるように3P%が40%を超えればかなりすごいとされます。
この結果を見るとやはり上位の選手は3Pをかなり決めているようです。Cが一番割合が高いのはびっくりですね。
個人的には直観に反した結果になったなと思います。一体どうしてこのような結果になったのでしょうか。
実はこの結果は3Pの試投数が考慮されていません。
極端な話、普段打たない選手がたまたま1本打った3Pが入ってそれ以降3Pを打たなければ3P%は100%になってしまいます。
どうやら正しく分析するためには試投数に制限を付ける必要がありそうです。
ということで最後に3P試投数に制限を付けて平均値を求めてみましょう。
3P試投数に制限を付けて平均値を求めよう
まずはそれぞれのポジションの平均3P試投数を求めてみましょう。
# 各ポジションの平均3P試投数を表示する(3PAは3P試投数のこと)
print("PG :", df_PG["3PA"].mean())
print("SG :", df_SG["3PA"].mean())
print("SF :", df_SF["3PA"].mean())
print("PF :", df_PF["3PA"].mean())
print("C :", df_C["3PA"].mean())
やはりポジションがPG~Cに行くにつれて3Pは打たなくなるようです。
ということでこれらの平均値以上に3Pを打っている選手についてのみ考えていきましょう。
#各ポジションの3P%ランキングTOP30を抽出する
df_PG_30 = df_PG[df_PG["3PA"] >= df_PG["3PA"].mean()].head(30)
df_SG_30 = df_SG[df_SG["3PA"] >= df_SG["3PA"].mean()].head(30)
df_SF_30 = df_SF[df_SF["3PA"] >= df_SF["3PA"].mean()].head(30)
df_PF_30 = df_PF[df_PF["3PA"] >= df_PF["3PA"].mean()].head(30)
df_C_30 = df_C[df_C["3PA"] >= df_C["3PA"].mean()].head(30)# 各ポジションの平均値を格納するリストを作成
data = []
# すべてのポジションに対して平均値を求める
for i in [df_PG_30, df_SG_30, df_SF_30, df_PF_30, df_C_30]:
data.append(i["3P%"].mean())
# 得られたデータをデータフレーム形式にする
mean_Pos_df_30 = pd.DataFrame(data = data, columns=["3P%"], index=pd.Index(["PG","SG", "SF", "PF", "C"], name = "ポジション"))
# データフレームの表示
mean_Pos_df_30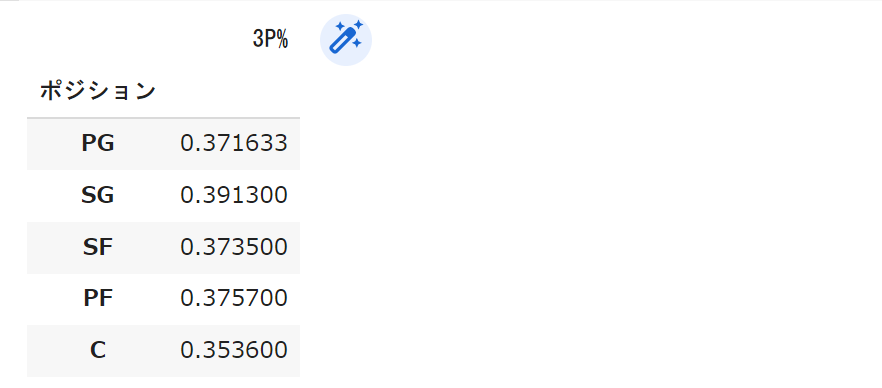
どうでしょうか。概ねぼくの想像と合致していました。
やはり3P試投数が原因だったようです。
このように条件を色々組み合わせることでより現実に近い結果を得ることができました。
とはいえまだ問題があって、PGの3P成功率がCの次に低くなっているようです。
これは一体どうしてなんでしょうか。条件を変えて色々いじってみると新たな発見ができて面白いと思います。
皆さんも自分の手を動かしてぜひやってみてください!
おわりに
いかがでしたでしょうか。
今回はNBAのデータの平均値を色々いじってみました。平均値だけでも意外といろいろなことができてしまいます。
もちろん平均値だけで物事を測るのは不十分ですが、平均値を知ることは重要です。
これを機に皆さんがデータ分析に興味を持ってくれたらうれしいです!
ぼくもこれらからも勉強頑張りたいと思います。
最後までこの記事を読んでくれてありがとうございました!
この記事が役に立ったら幸いです。




