こんにちは!しゅんです!
このブログでは経営工学を勉強している現役理系大学生が、経営工学に関することを色々話していきます!
ぼくが経営工学を勉強している中で感じたことや、興味深かったことを皆さんと共有出来たら良いなと思っています。
そもそも経営工学とは何なのでしょうか。Wikipediaによると
経営工学(けいえいこうがく、英: engineering management)は、人・材料・装置・情報・エネルギーを総合したシステムの設計・改善・確立に関する活動である。そのシステムから得られる結果を明示し、予測し、評価するために、工学的な分析・設計の原理・方法とともに、数学、物理および社会科学の専門知識と経験を利用する。
引用元 : 経営工学 – Wikipedia
長々と書いてありますが、要は経営、経済の課題を理系的な観点から解決する学問です。

今回の記事はNBAのスタッツを使ってデータ分析をしてみたいと思います!
経営工学とは少し離れるかもしれませんが、データ分析に興味がある人、NBAに興味がある人はぜひ今回の記事を読んでみてください!!!
経営工学についての別の記事もあるのでぜひこちらも読んでみてください!
基本統計量ってなに?
基本統計量とはその名の通り統計をするに当たってまず求めるような量のことです。
以下のように中学、高校の数学で勉強するものがほとんどです。
・平均値
・中央値
・最頻値
・最大値、最小値
・分散、標準偏差
データの特徴を知るうえで非常に重要な指標になります。また簡単に値を求めることができるのでデータの分析をするときにはまず基本統計量を調べたりします。
ということで今回扱うNBAのデータについても基本統計量をいくつか求めてみましょう。
今回の分析はgoogle colabを使ってやりたいと思います。
この記事は前の記事からの続きなので、前の記事から読んだ方が分かりやすいと思います!
平均値を求めよう
それでは早速平均値を求めてみましょう。
全員の数値を全部足して人数で割った数

ということでやってみましょう。今回はFG%, 3P%, 2P%, FT%, PTSの5つの指標について平均値を求めます。
# 平均値を計算したい指標をまとめる(今回はFG%, 3P%, 2P%, FT%, PTSの平均を求める)
for i in ["FG%", "3P%", "2P%", "FT%", "PTS"]:
# 平均値を表示する(meanは平均値を表す)
print(i, df[i].mean())
ということで各スタッツの平均値が求まりました。みなさんが想像した値に比べてどうでしたかね。
ぼくは思ったよりも3P決めてたなという印象でした。こんなもんなんですかね。
中央値を求めよう
それでは中央値を求めてみましょう。
全員の数値を小さい順に並べたときにちょうど真ん中にある数
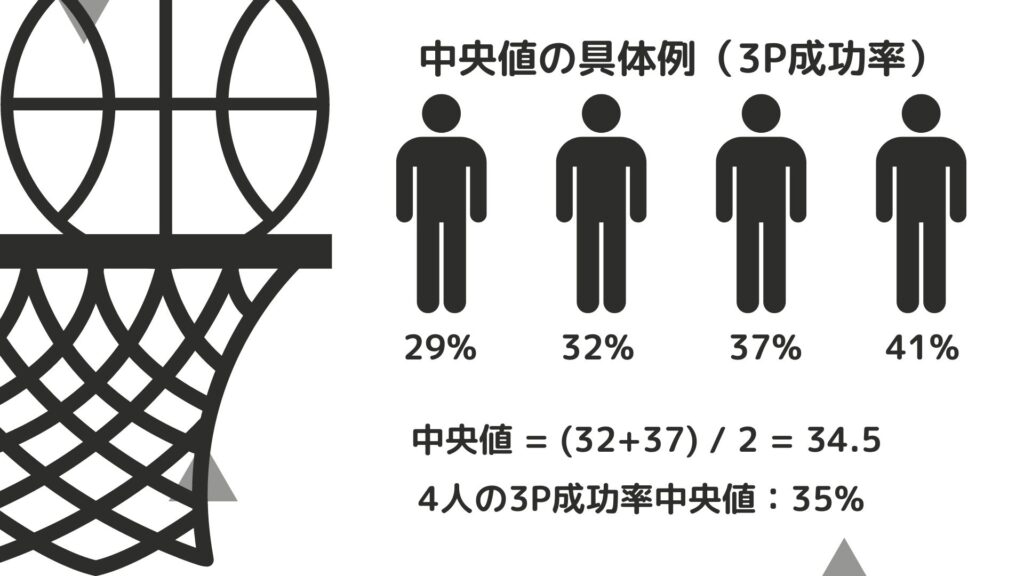
上の図のように求めることができます。
データ数が偶数のときはちょうど真ん中の数が存在しません。
その場合は真ん中の2つの数の平均値をそのデータの中央値とします。
(データ数が100の中央値は50番目と51番目の数字の平均値を求れば良い。)
ということでやってみましょう。今回はFG%, 3P%, 2P%, FT%, PTSの5つの指標について中央値を求めます。
# 中央値を計算したい指標をまとめる(今回はFG%, 3P%, 2P%, FT%, PTSの中央値を求める)
for i in ["FG%", "3P%", "2P%", "FT%", "PTS"]:
# 中央値を表示する(medianは中央値を表す)
print(i, df[i].median())
ということで各スタッツの中央値が求まりました。平均値と見比べてみるとどうでしょうか。
平均値と比べてPTSの中央値が少し低いですね。ということは得点力が高い一部の選手が平均を押し上げていると言うことでしょうか。
こんな感じで必ずしも平均値と中央値が一致するとは限りません。データの分布によって大きく変わることもあります。
例えば日本の年収の平均値は445万円ほどですが、中央値は397万円ほどで平均値と中央値で約48万円ほどの差があります。
年収の下限は0ですが上限は存在しないので、一部の超お金持ちが平均値を押し上げていることがこれだけの差を生む原因になっています。
平均値は必ずしもデータの真ん中を表すわけではないことに注意してください。
参考文献:【2022年】日本の平均年収・年収中央値は?職業年齢別の給料比較 (kikankou.co.jp)
最大値、最小値を求めよう
ということで次に最大値、最小値を求めてみましょう。
最大値:データの中で数値が最大のもの
最小値:データの中で数値が最小のもの
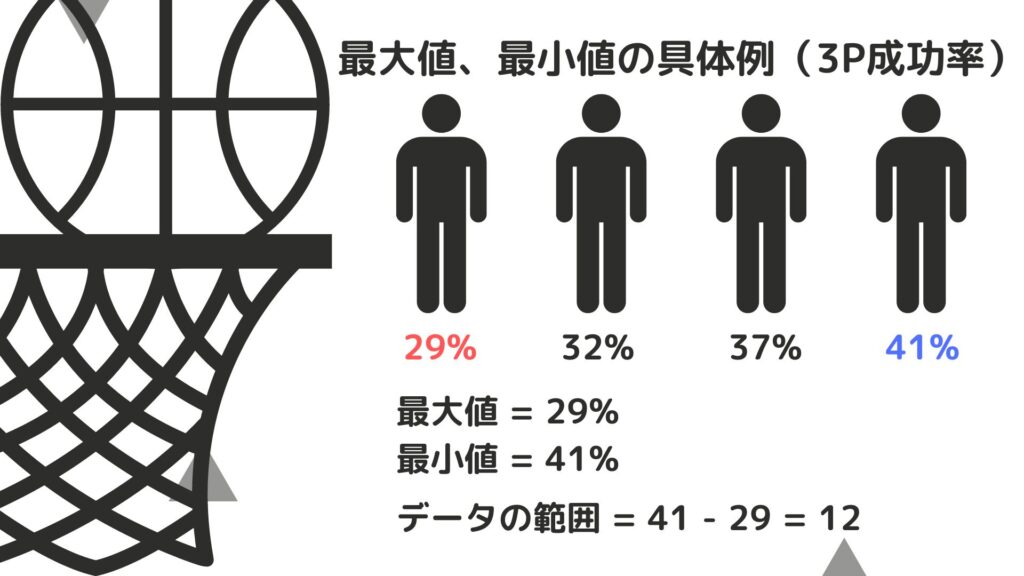
上の図のように求めることができます。最大値から最小値を引いたものをデータの範囲と呼びます。
ということでやってみましょう。今回はFG%, 3P%, 2P%, FT%, PTSの5つの指標について最大値と最小値を求めます。
# 最大値、最小値を計算したい指標をまとめる(今回はFG%, 3P%, 2P%, FT%, PTSの最大値、最小値を求める)
for i in ["FG%", "3P%", "2P%", "FT%", "PTS"]:
# 最大値を表示する(maxは最大値を表す)
print(i, " max :",df[i].max())
# 最小値を表示する(minは最小値を表す)
print(i, " min :",df[i].min())
ということで最大値と最小値が求まりました。大体予想はついていましたが最高値が1.0で最小値が0.0になる指標が多いですね。
0とか1とかはそもそも試投数が少なすぎるのであまりデータとして意味を持ちません。
ちなみに0と1というデータ値を除いた中での最大値、最小値を求めることもできます。ある条件の中での最大値、最小値の求め方は調べればたくさん出てくるので気になった場合は是非調べてみてください。
気が向いたらぼくのブログでもやってみようと思います笑
PTSの最大値が30.6になっていますね。21-22シーズンの得点王はエンビードだったのでこの30.6という数値はエンビードでしょうか。
ちょっと調べてみましょう。
# PTSの値がPTSの最大値になっている行のPlayer名だけ抽出する
df[df["PTS"] == df["PTS"].max()]["Player"]
ということでやはりエンビードでしたね。
分散、標準偏差を求めよう
ということで最後に分散と標準偏差を求めてみましょう。
分散 : データが平均からどれくらい離れているか
標準偏差 : 分散にルートを取ったもの
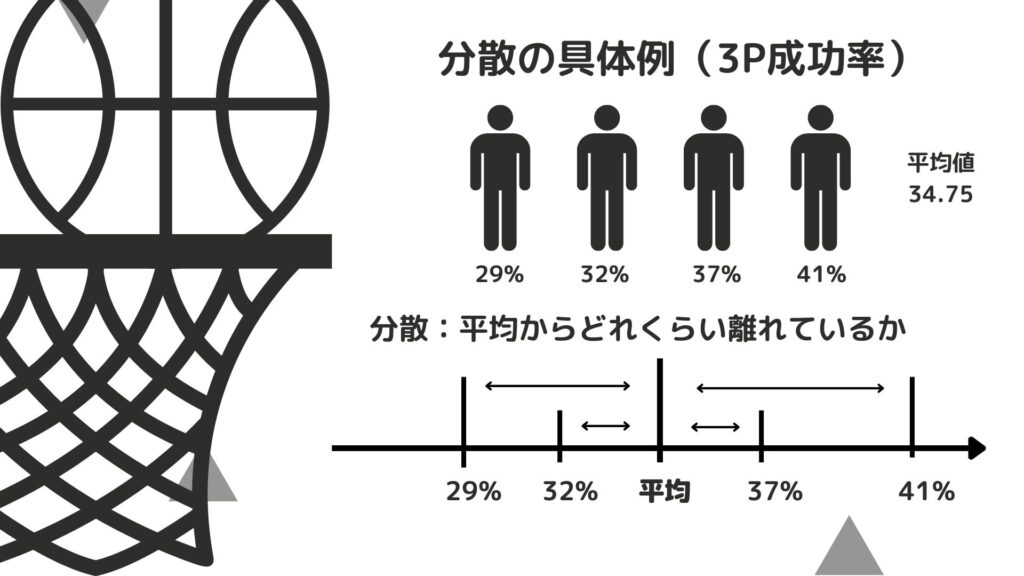
分散、標準偏差を求めるのはこれまでと比べて少し複雑なので計算式は省いてイメージだけ画像にしました。
分散、標準偏差を見ることでデータの分布がある程度把握できます。
例えば4つの数字が全部10の場合と4つの数字がそれぞれ-1000, -1000, 1000, 1040の場合、平均値は両方とも10です。
しかしこの2つのデータは全く違います。そこで登場するのが分散です。
前者の分散は0で後者の分散は非常に大きな値を取ります。分散を求めることでデータの違いを見つけることができました。
ところで標準偏差は分散にルートを取ります。なぜでしょうか。
分散は計算する過程で数値の2乗をとります。そのため例えばデータの単位がcmの場合、分散の単位がc㎡になって正常な比較ができなくなります。
ということで同じ単位に直すためにルートを取るわけです。
データの分析ではこのあと相関係数を求めたりしますが、そのときに用いるのは標準偏差の方です。
分散、標準偏差の具体的な求め方調べればい分かりやすいサイトが出てきます。
また高校の数Ⅰのデータの分析の範囲でも勉強できると思います。
長くなってしまいましたが、実際にgoogle colabで計算してみましょう。
# 分散、標準偏差を計算したい指標をまとめる(今回はFG%, 3P%, 2P%, FT%, PTSの分散、標準偏差を求める)
for i in ["FG%", "3P%", "2P%", "FT%", "PTS"]:
# 分散を表示する(varは分散を表す)
print(i, " 分散 :",df[i].var(ddof = 0))
# 標準偏差を表示する(stdは標準偏差を表す)
print(i, " 標準偏差 :",df[i].std(ddof = 0))
ということで求まりました。(コードにあるddofは今はまだ気にしなくてよいです。)
そもそもPTSは%表記じゃないので他の指標と比べてもあまり意味がないです。
ということで他の4つの指標を見てみるとやはりFT%が一番標準偏差が大きいですね。
これは単純にFtがうまい人と下手な人の差が激しいからですね。例えば3Pがどんなにうまい人でも50%超えることはなかなかないです。
そのため3P%は基本的には0~0.5の間で分布していますが、FTは90%以上も決める選手がちょくちょく出てきます。
そのためFT%は基本的には0~0.9の間で分布するはずです。そういうわけで必然的にFT%が一番標準偏差が大きくなっているのだと考えられます。
おわりに
いかがでしたでしょうか。
今回の記事では基本統計量について色々と解説していきました。
ここらへんはデータ分析をする上で前提となる知識なのでぜひとも知っておくべきだと思います!
色々とデータに条件を付けた上でこれらの基本統計量を求めてみると新たな発見があるかもしれません。
ぜひ調べてみてください!
最後までこの記事を読んでくれてありがとうございました。
この記事が役に立ったら幸いです。





テスト
テスト あいうえお